leetcode 刷题day44动态规划Part13( 647. 回文子串、516.最长回文子序列)
647. 回文子串
动规五部曲:
1、确定dp数组(dp table)以及下标的含义
按照之前做题的惯性,定义dp数组的时候很自然就会想题目求什么,就如何定义dp数组。但是对于本题来说,这样定义很难得到递推关系,dp[i] 和 dp[i-1] ,dp[i + 1] 看上去都没啥关系。
在判断字符串S是否是回文时,如果知道 s[1],s[2],s[3] 子串是回文,只需要比较 s[0]和s[4]这两个元素是否相同,如果相同的话,这个字符串s 就是回文串。此时找到了一种递归关系,判断一个字符串下标范围[i,j]是否回文,依赖于子字符串下标范围[i + 1, j - 1]是否是回文。
所以dp数组要定义成一个二维dp数组。布尔类型的dp[i][j]:表示区间范围[i,j] (注意是左闭右闭)的子串是否是回文子串,如果是dp[i][j]为true,否则为false。
2、确定递推公式
- 当s[i]与s[j]不相等,dp[i][j]一定是false。
- 当s[i]与s[j]相等时,这就复杂一些了,有如下三种情况
情况一:下标i 与 j相同,同一个字符例如a,当然是回文子串
情况二:下标i 与 j相差为1,例如aa,也是回文子串
情况三:下标:i 与 j相差大于1的时候,例如cabac,此时s[i]与s[j]已经相同了,看dp[i + 1][j - 1]是否为true。
3、dp数组如何初始化
dp[i][j]初始化为false
4、确定遍历顺序
从递推公式中可以看出情况三是根据dp[i + 1][j - 1]是否为true对dp[i][j]进行赋值的。dp[i + 1][j - 1] 在 dp[i][j]的左下角。所以从下到上,从左到右遍历,保证dp[i + 1][j - 1]都是经过计算的。
举例aaa,先从最后一个a开始遍历,然后第2个a,最后是第1个a
因为dp[i][j]的定义,所以j一定是大于等于i的,那么在填充dp[i][j]的时候一定是只填充右上半部分。
5、举例推导dp数组
代码如下:
class Solution {public int countSubstrings(String s) {boolean[][] dp=new boolean[s.length()][s.length()];int result=0;for(int i=s.length();i>=0;i--){for(int j=i;j<s.length();j++){if(s.charAt(i)==s.charAt(j) && (j-i<=1 || dp[i+1][j-1])){result++;dp[i][j]=true;}}}return result;}
}
还可以考虑使用中心扩散法。
确定回文串-就是找中心然后向两边扩散看是不是对称。
在遍历中心点的时候,要注意中心点有两种情况:一个元素可以作为中心点,两个元素也可以作为中心点。对每一个元素作为中心点的情况进行遍历。
代码如下:
class Solution {public int countSubstrings(String s) {int reslut=0;for(int i=0;i<s.length();i++){reslut+=extend(s,i,i,s.length());reslut+=extend(s,i,i+1,s.length());}return reslut;}public int extend(String s,int i,int j,int n){int res=0;while(j<n && i>=0 && s.charAt(i)==s.charAt(j)){res++;i--;j++;}return res;}
}
516.最长回文子序列
思路:该题与上一题的区别在于子序列是删除某些元素得到的序列。
动规五部曲分析如下:
1、确定dp数组(dp table)以及下标的含义
dp[i][j]:字符串s在[i, j]范围内最长的回文子序列的长度为dp[i][j]。
2、确定递推公式
在判断回文子串的题目中,关键逻辑就是看s[i]与s[j]是否相同。
- 如果s[i]与s[j]相同,那么dp[i][j] = dp[i + 1][j - 1] + 2;
- 如果s[i]与s[j]不相同,说明s[i]和s[j]的同时加入并不能增加[i,j]区间回文子序列的长度,分别加入s[i]、s[j]看看哪一个可以组成最长的回文子序列。加入s[j]的回文子序列长度为dp[i + 1][j];加入s[i]的回文子序列长度为dp[i][j - 1]。dp[i][j]取最大的,即:dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
因为遍历了每个i和j,且考虑了不取左边或右边的情况,因而可以实现子序列不连续。
3、dp数组如何初始化
首先要考虑当i 和j 相同的情况,从递推公式:dp[i][j] = dp[i + 1][j - 1] + 2; 可以看出递推公式计算不到 i 和j相同时候的情况,所以需要手动初始化一下,当i与j相同,dp[i][j]=1,即:一个字符的回文子序列长度就是1。
4、确定遍历顺序
和上一题一样,从下到上,从左到右遍历。
5、举例推导dp数组
代码如下:
class Solution {public int longestPalindromeSubseq(String s) {int[][] dp=new int[s.length()][s.length()];for(int i=0;i<s.length();i++){dp[i][i]=1;}for(int i=s.length();i>=0;i--){for(int j=i+1;j<s.length();j++){if(s.charAt(i)==s.charAt(j)) dp[i][j]=dp[i+1][j-1]+2;else dp[i][j]=Math.max(dp[i][j-1],dp[i+1][j]);}}return dp[0][s.length()-1];}
}
相关文章:
)
leetcode 刷题day44动态规划Part13( 647. 回文子串、516.最长回文子序列)
647. 回文子串 动规五部曲: 1、确定dp数组(dp table)以及下标的含义 按照之前做题的惯性,定义dp数组的时候很自然就会想题目求什么,就如何定义dp数组。但是对于本题来说,这样定义很难得到递推关系&#x…...

华为OD机试真题---关联子串
华为OD机试中的“关联子串”题目是一个考察字符串处理和算法理解的经典问题。以下是对该题目的详细解析: 一、题目描述 给定两个字符串str1 和 str2,如果字符串 str1 中的字符, 经过排列组合后的字符串中只要有一个是 str2 的子串ÿ…...

【OpenAI】第二节(Token)什么是Token?如何计算ChatGPT的Token?
深入解析:GPT如何计算Token数?让你轻松掌握自然语言处理的核心概念!🚀 在当今的人工智能领域,GPT(Generative Pre-trained Transformer)无疑是最受关注的技术之一。无论是在文本生成、对话系统…...

GraphRAG + Ollama + Groq 构建知识库 续篇 利用neo4j显示知识库
GraphRAG Ollama Groq 构建知识库 在上一篇文章中,我们详细介绍了如何创建一个知识库。尽管知识库已经建立,但其内容的可视化展示尚未实现。我们无法直接看到知识库中的数据,也就无法判断这些数据是否符合我们的预期。为了解决这个问题&…...

工业以太网之战:EtherCAT是如何杀出重围的?
前言 EtherCAT 是一种开放的实时工业以太网协议,由德国倍福公司开发并在 2003 年 4 月的汉诺威工业博览会上首次亮相,目前由 EtherCAT 技术协会(ETG)进行维护和推广。经过 21 年的不断发展,EtherCAT 显示出极强的生命…...
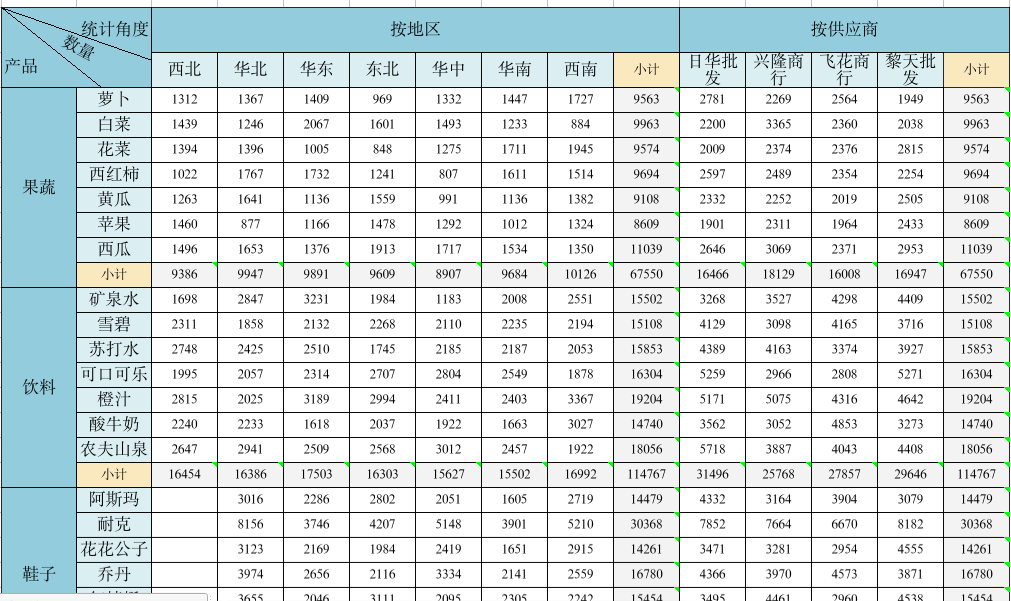
轻量级可视化数据分析报表,分组汇总表!
什么是可视化分组汇总表? 可视化分组汇总表,是一种结合了数据分组、聚合计算与视觉呈现功能的数据分析展示功能。它能够按照指定的维度(如时间、地区、产品类型等)对数据进行分组,还能自动计算各组的统计指标…...

初始Python篇(4)—— 元组、字典
找往期文章包括但不限于本期文章中不懂的知识点: 个人主页:我要学编程(ಥ_ಥ)-CSDN博客 所属专栏: Python 目录 元组 相关概念 元组的创建与删除 元组的遍历 元组生成式 字典 相关概念 字典的创建与删除 字典的遍历与访问 字典…...

C#中正则表达式
在C#中,正则表达式由 System.Text.RegularExpressions 命名空间提供,可以使用 Regex 类来处理正则表达式。以下是一些常见的用法及示例。 C# 中使用正则表达式的步骤: 引入命名空间: using System.Text.RegularExpressions; 创…...

【python写一个带有界面的计算器】
python写一个带有界面的计算器 为了创建一个带有图形用户界面(GUI)的计算器,我们可以使用Python的tkinter库。tkinter是Python的标准GUI库,它允许我们创建窗口、按钮、文本框等GUI元素。 下面是一个简单的带有GUI的计算器示例&a…...

K230获取单摄像头的 3 个通道图像并显示在 HDMI 显示器上
本示例打开摄像头,获取 3 个通道的图像并显示在 HDMI 显示器上。通道 0 采集 1080P 图像,通道 1 和通道 2 采集 VGA 分辨率的图像并叠加在通道 0 的图像上。 # Camera 示例 import time import os import sysfrom media.sensor import * from media.dis…...
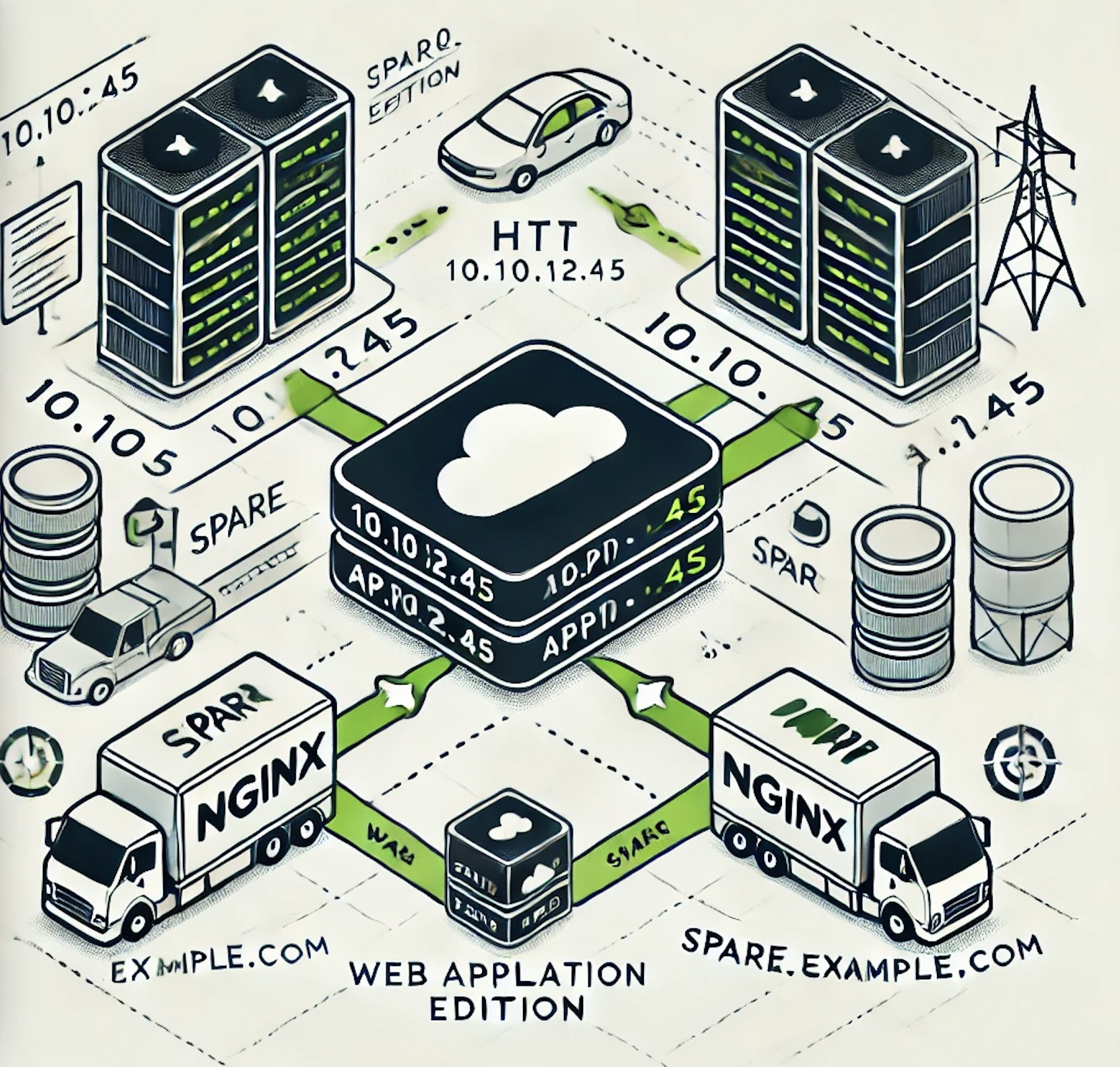
nginx中的HTTP 负载均衡
HTTP 负载均衡:如何实现多台服务器的高效分发 为了让流量均匀分配到两台或多台 HTTP 服务器上,我们可以通过 NGINX 的 upstream 代码块实现负载均衡。 方法 在 NGINX 的 HTTP 模块内使用 upstream 代码块对 HTTP 服务器实施负载均衡: upstr…...

package.json 里的 dependencies和devDependencies区别
dependencies(依赖的意思): 通过 --save 安装,是需要发布到生产环境的。 比如项目中使用react,那么没有这个包的依赖就会报错,因此把依赖写入dependencies npm install <package-name>// 缩写 np…...
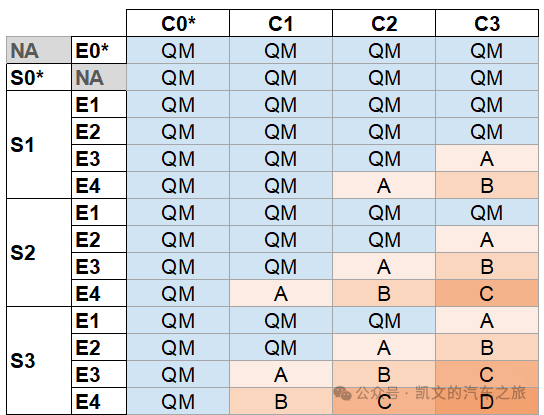
【功能安全】HARA分析中的SEC如何确认
目录 01 SEC介绍 02 SEC怎么定义 📖 推荐阅读 01 SEC介绍 SEC定义 S代表safety,E指的是Exposure,C指的是Controllability ASIL等级就是基于SEC三个参数确定下来的。 计算公式:10=D,9=C,8=B,7=A,<7=QM 举例:S3-C2-E4,即3+2+4=9,ASIL C 02 SEC怎么定义 Safe…...

阿里云Docker镜像源安装Docker的步骤
阿里云 Docker 镜像源安装 Docker 的步骤: 1. 更新包管理器: sudo apt update 2. 安装 Docker 的依赖包: sudo apt install apt-transport-https ca-certificates curl gnupg lsb-release 3. 添加阿里云 Docker 镜像源 GP…...

得一微全资子公司硅格半导体携手广东工业大学,荣获省科学技术奖一等奖
10月17日,全省科技大会在广州召开,会上颁发了2023年度广东省科学技术奖。得一微电子旗下全资子公司深圳市硅格半导体有限公司(以下简称“硅格半导体”)与广东工业大学(以下简称:广工大)携手多家…...

@SneakyThrows不合理使用,是真的坑
public static void main(String[] args) {int a 1;int b 2;String result getResult(a, b);System.out.println(result);}SneakyThrowspublic static String getResult(Integer a,Integer b){if (a.equals(b)){return "成功!";}else{throw new Interru…...
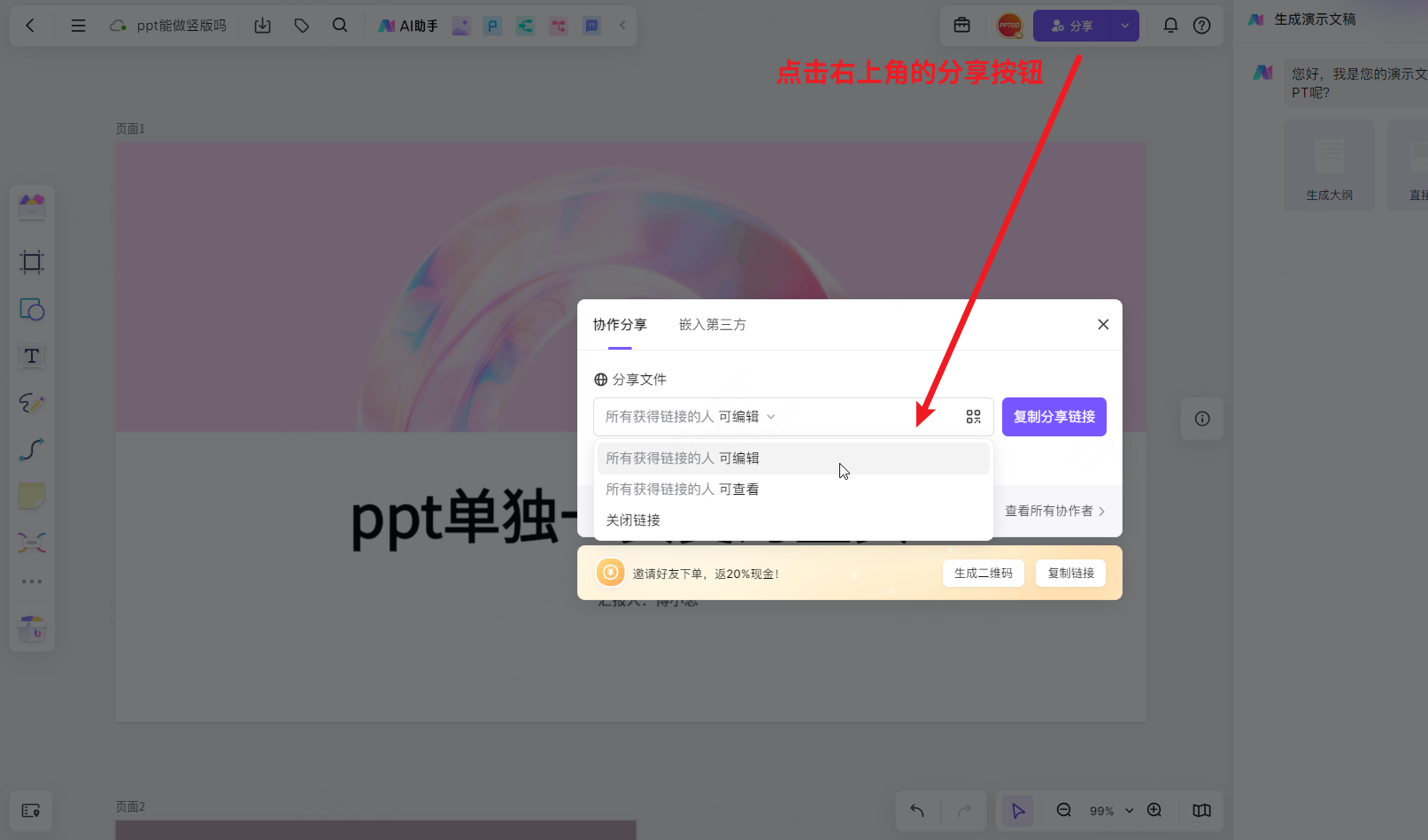
怎么把ppt页面切换为竖页?首推使用这个在线ppt工具!
熟悉ppt的朋友都知道,最常见的ppt演示文稿为横版样式,且一旦确定了ppt的版式,后续所有页面会保持相同的大小,但有时横版不能满足我们需求,想单独把其中一页或多页变为竖页,Office Powerpoint就无能为力了。…...

【JavaEE】——自定义协议方案、UDP协议
阿华代码,不是逆风,就是我疯 你们的点赞收藏是我前进最大的动力!! 希望本文内容能够帮助到你!! 目录 一:自定义协议 1:自定义协议 (1)交互哪些信息 &…...

python爬虫快速入门之---Scrapy 从入门到包吃包住
python爬虫快速入门之—Scrapy 从入门到包吃包住 文章目录 python爬虫快速入门之---Scrapy 从入门到包吃包住一、scrapy简介1.1、scrapy是什么?1.2、Scrapy 的特点1.3、Scrapy 的主要组件1.4、Scrapy 工作流程1.5、scrapy的安装 二、scrapy项目快速入门2.1、scrapy项目快速创建…...

【Photoshop——肤色变白——曲线】
1. 三通道曲线原理 在使用RGB曲线调整肤色时,你可以通过调整红、绿、蓝三个通道的曲线来实现黄皮肤到白皮肤的转变。 黄皮肤通常含有较多的红色和黄色。通过减少这些颜色的量,可以使肤色看起来更白。 具体步骤如下: 打开图像并创建曲线调…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

Docker拉取MySQL后数据库连接失败的解决方案
在使用Docker部署MySQL时,拉取并启动容器后,有时可能会遇到数据库连接失败的问题。这种问题可能由多种原因导致,包括配置错误、网络设置问题、权限问题等。本文将分析可能的原因,并提供解决方案。 一、确认MySQL容器的运行状态 …...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

若依登录用户名和密码加密
/*** 获取公钥:前端用来密码加密* return*/GetMapping("/getPublicKey")public RSAUtil.RSAKeyPair getPublicKey() {return RSAUtil.rsaKeyPair();}新建RSAUti.Java package com.ruoyi.common.utils;import org.apache.commons.codec.binary.Base64; im…...

深度解析云存储:概念、架构与应用实践
在数据爆炸式增长的时代,传统本地存储因容量限制、管理复杂等问题,已难以满足企业和个人的需求。云存储凭借灵活扩展、便捷访问等特性,成为数据存储领域的主流解决方案。从个人照片备份到企业核心数据管理,云存储正重塑数据存储与…...

CSS 工具对比:UnoCSS vs Tailwind CSS,谁是你的菜?
在现代前端开发中,Utility-First (功能优先) CSS 框架已经成为主流。其中,Tailwind CSS 无疑是市场的领导者和标杆。然而,一个名为 UnoCSS 的新星正以其惊人的性能和极致的灵活性迅速崛起。 这篇文章将深入探讨这两款工具的核心理念、技术差…...
