typescript 中封装一个 class 来解析接口响应数据
在TypeScript中,封装一个类来解析接口响应数据是一个常见的做法,它允许你将与接口响应相关的逻辑封装在一个可复用的单元中。下面是一个示例,展示了如何定义一个TypeScript类来解析一个假设的API接口响应数据。
首先,我们定义一个接口来描述从API接收到的数据形状:
interface UserData {id: number;name: string;email: string;// 可以根据需要添加更多属性
}
然后,我们创建一个类UserResponseParser,它接收一个符合UserData接口的对象作为输入,并提供方法来访问或处理这些数据:
class UserResponseParser {private userData: UserData; // 使用private来限制外部直接访问constructor(rawData: UserData) {if (!rawData || typeof rawData !== 'object') {throw new Error('Invalid raw data provided to UserResponseParser');}this.userData = rawData;}// 公开一个方法来获取用户的名字getName(): string {return this.userData.name;}// 公开一个方法来获取用户的邮箱getEmail(): string {return this.userData.email;}// 可以根据需要添加更多方法// 例如,一个方法用于获取用户的完整信息(以字符串形式)getUserInfoAsString(): string {return `User ID: ${this.userData.id}, Name: ${this.userData.name}, Email: ${this.userData.email}`;}
}// 示例用法
const rawUserData: UserData = {id: 1,name: 'John Doe',email: 'john.doe@example.com'
};try {const userParser = new UserResponseParser(rawUserData);console.log(userParser.getName()); // 输出: John Doeconsole.log(userParser.getEmail()); // 输出: john.doe@example.comconsole.log(userParser.getUserInfoAsString()); // 输出: User ID: 1, Name: John Doe, Email: john.doe@example.com
} catch (error) {console.error('Error parsing user data:', error.message);
}
在这个例子中,UserResponseParser类有一个私有属性userData,它存储了从API接收到的原始数据。构造函数接受一个UserData类型的参数,并将其存储在userData属性中。然后,类提供了几个公开的方法来访问这些数据,如getName和getEmail。此外,还提供了一个getUserInfoAsString方法来将用户的完整信息格式化为一个字符串。
通过使用TypeScript,我们得到了类型安全和自动完成等好处,这有助于减少错误并提高开发效率。同时,将逻辑封装在类中也有助于保持代码的模块化和可重用性。
相关文章:

typescript 中封装一个 class 来解析接口响应数据
在TypeScript中,封装一个类来解析接口响应数据是一个常见的做法,它允许你将与接口响应相关的逻辑封装在一个可复用的单元中。下面是一个示例,展示了如何定义一个TypeScript类来解析一个假设的API接口响应数据。 首先,我们定义一个…...
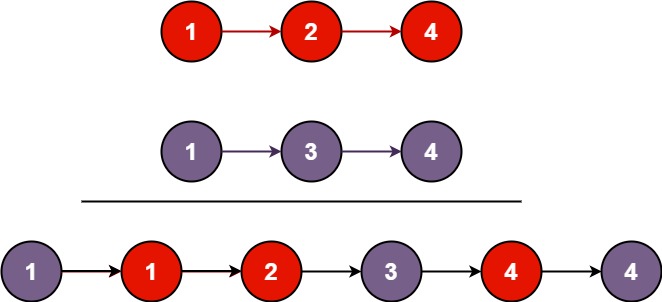
[LeetCode] 21. 合并两个有序链表
题目描述: 将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 示例 1: 输入:l1 [1,2,4], l2 [1,3,4] 输出:[1,1,2,3,4,4]示例 2: 输入:l1 [], l2 […...
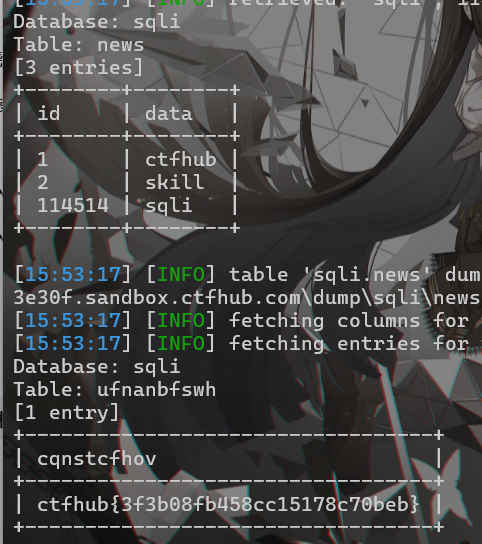
CTFHUB技能树之SQL——MySQL结构
开启靶场,打开链接: 先判断一下是哪种类型的SQL注入: 1 and 11# 正常回显 1 and 12# 回显错误,说明是整数型注入 判断一下字段数: 1 order by 2# 正常回显 1 order by 3# 回显错误,说明字段数是2列 知道…...

Git小知识:合理的分支命名约定
前言:创建新分支时,对 Git 分支进行合理的命名非常重要,应选择有描述性的名称,因为它可以帮助团队成员更好地理解分支的目的和内容,以便将来回顾时能立即明白分支的目的。以下是一些常见的分支命名约定: 功…...

Ubuntu如何显示pcl版本
终端输入: apt-cache show libpcl-dev可以看到,Ubuntu20.04,下载的pcl,应该都是1.10版本的...

wordcloud 字体报错
wordcloud 字体报错 词云库报错:Only supported for TrueType fonts字体文件问题pillow版本的问题wordcloud版本问题(我的最终解决方案) 词云库报错:Only supported for TrueType fonts 字体文件问题 解决方法 写绝对路径 &…...

使用Matplotlib绘制极轴散点图
散点图对于理解数据可视化中变量之间的相互作用至关重要。虽然散点图经常在笛卡尔坐标中创建,但我们也可以使用Matplotlib在极轴上创建散点图。有了这个功能,人们可以以创新的方式查看圆形或角形数据,例如周期性趋势或定向模式。在本文中&…...

Elasticsearch入门:增删改查详解与实用场景
引言 在我之前做社交架构设计的时候,我们有一项关键且必要的需求:需要存储并记录用户的所有聊天记录。这些记录不仅用于业务需求,也承担了风控审查的职责。因此,在架构设计中,我们需要考虑每天海量的聊天消息量&#…...

【AI论文精读6】SELF-RAG(23.10)附录
【AI论文解读】【AI知识点】【AI小项目】【AI战略思考】 P1,P2,P3 附录 A SELF-RAG 细节 A.1 反思标记(reflection tokens) 反思标记的定义 下面我们提供了反思标记类型和输出标记的详细定义。前三个方面将在每个片段…...

sql-labs靶场第十七关测试报告
目录 一、测试环境 1、系统环境 2、使用工具/软件 二、测试目的 三、操作过程 1、寻找注入点 2、注入数据库 ①寻找注入方法 ②爆库,查看数据库名称 ③爆表,查看security库的所有表 ④爆列,查看users表的所有列 ⑤成功获取用户名…...

面试官:MySQL一次到底插入多少条数据合适啊?
前言 大家好!在互联网时代,我们的每一个动作,无论是浏览网页、分享动态、点赞、购物或者搜索信息,都会在背后产生数据。这些数据,根据其用途和重要性,可能会被储存到不同的地方,其中最常见的存…...
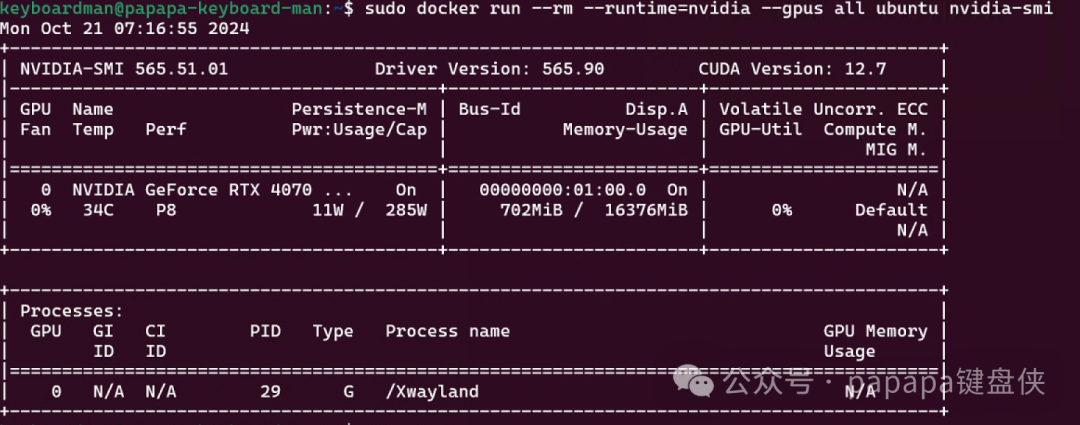
WSL2 构建Ubuntu系统-轻量级AI运行环境
环境:Win11 软件:WSL2 安装环境:Ubuntu 22.04 检查电脑是否开启虚拟化 打开:任务管理器->性能->CPU CPU 开启虚拟化(通常默认是开启的,如果没有开启需要BIOS开启) 虚拟化设置࿰…...

什么是凸二次规划问题
我们从凸二次规划的基本概念出发,然后解释它与支持向量机的关系。 一、凸二次规划问题的详细介绍 凸二次规划问题是优化问题的一类,目标是最小化一个凸的二次函数,受一组线性约束的限制。凸二次规划是一类特殊的二次规划问题,其…...

解决 Elasticsearch cluster_block_exception 错误的终极指南
Elasticsearch 是一个功能强大的分布式搜索引擎,广泛应用于全文检索、实时分析等场景。 尽管如此,像任何复杂系统一样,它也会遇到一些运行问题,其中较为常见且影响较大的就是 cluster_block_exception 错误。 本文将深入解析这种错…...

QT sql驱动错误QMYSQL driver not loaded
引用文章QMYSQL driver not loaded 根据引用文章,到在编译QT mysql.pro的源码步骤时,构建没有报错,但是在对应的文件夹内没有找到编译好的dll文件,经过全电脑搜寻,找到在此文件夹内。 遇到同样错误的朋友可以找找QT安…...

数据驱动,漫途能耗管理系统打造高效节能新生态!
在我国能源消耗结构中,工业企业所占能耗比例相对较大。为实现碳达峰、碳中和目标,工厂需强化能效管理,减少能耗与成本。高效的能耗管理系统通过数据采集与分析,能实时监控工厂能源使用及报警情况,为节能提供数据。构建…...
PH47代码框架软件二次开发极简教程
1. 教程说明 本教程适用于对飞控及Stm32程序设计比较熟悉的二次开发者快速掌握PH47框架的使用要点。本教程仅对PH47框架中最主要的二次开发特性进行简要说明,建议与框架中\DevStudio\Algorithms\Controller_Demo.cpp(.h)示例代码配合学习。关于二次开发特性中的详细…...

SQL Server-导入和导出excel数据-注意事项
环境: win10,SQL Server 2008 R2 之前写过的放在这里: SqlServer_陆沙的博客-CSDN博客 https://blog.csdn.net/pxy7896/category_12704205.html 最近重启ASP.NET项目,在使用sql server导出和导入数据时遇到一些问题,特…...

Linux系统:配置Apache支持CGI(Ubuntu)
配置Apache支持CGI 根据以下步骤配置,实现Apache支持CGI 安装Apache: 可参照文章: Ubuntu安装Apache教程。执行以下命令,修改Apache2配置文件000-default.conf: sudo vim /etc/apache2/sites-enabled/000-default.con…...

qt 序列化和反序列化
序列化:QByteArray buffer; QBuffer bufferDevice(&buffer); bufferDevice.open(QIODevice::WriteOnly); QDataStream out(&bufferDevice); out.setVersion(QDataStream::Qt_5_13); 反序列化: void deserialize(const QByteArray &buffer) {…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

Vue 3 + WebSocket 实战:公司通知实时推送功能详解
📢 Vue 3 WebSocket 实战:公司通知实时推送功能详解 📌 收藏 点赞 关注,项目中要用到推送功能时就不怕找不到了! 实时通知是企业系统中常见的功能,比如:管理员发布通知后,所有用户…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
