制程质量管理方案设计

质量管理系统框架——QMS
涵盖产生产制造体系的全生命周期的质量管理过程
与SAP、WMS、MES、OA等业务系统进行集成,整合各业务系统中的质量信息
利用整合的全价值链质量信息,寻找质量改进点和质量创新点

系统功能模块管理
系统管理:用户管理、角色管理、权限管理、部门管理、职务管理、系统参数
检验基础:检验类型、检验条件、检验方法、检验标准、检验项目、判断标准、原因缺陷、检验设备、检验组
工艺基础:工序管理、设备管理、物料管理
检验管理:检验任务、中控台
报表管理:检验报表、spc等
计划管理(拓展):检验计划配置
生命周期管理
1、初始阶段需完成基础模块如OA与QMS用户组织架构的打通实现
2、完成生产制造系统MES与QMS的对接,实现检验基础如工序、物料、设备的传输,继而实现工序与对应检验项目,物料与工序的关系绑定
3、根据生产报工推送检验任务,进而展开检验单的创建与检验操作
4、检验完成反推生产系统(或SAP)进行入库管理
5、检验数据分析及工艺改进
相关文章:

制程质量管理方案设计
质量管理系统框架——QMS 涵盖产生产制造体系的全生命周期的质量管理过程 与SAP、WMS、MES、OA等业务系统进行集成,整合各业务系统中的质量信息 利用整合的全价值链质量信息,寻找质量改进点和质量创新点 系统功能模块管理 系统管理:用户管理…...

uniapp移动端优惠券! 附源码!!!!
本文为常见的移动端uniapp优惠券,共有6种优惠券样式(参考了常见的优惠券),文本内容仅为示例,您可在此基础上调整为你想要的文本 预览效果 通过模拟数据,实现点击使用优惠券让其变为灰色的效果(模…...

【分布式技术】中间件-zookeeper安装配置
文章目录 安装部署1. 安装ZooKeeper2. 配置ZooKeeper3. 启动ZooKeeper服务器4. 使用ZooKeeper命令行客户端5. 使用ZooKeeper的四个基本操作6. ZooKeeper集群模式7. 安全和权限8. 监控和日志 相关文献 安装部署 在Linux环境中操作ZooKeeper通常涉及以下几个方面: 1…...

高等数学 7.6高阶线性微分方程
文章目录 一、线性微分方程的解的结构*二、常数变易法 方程 d 2 y d x 2 P ( x ) d y d x Q ( x ) f ( x ) (1) \cfrac{\mathrm{d}^2 y}{\mathrm{d}x^2} P(x) \cfrac{\mathrm{d}y}{\mathrm{d}x} Q(x) f(x) \tag{1} dx2d2yP(x)dxdyQ(x)f(x)(1) 叫做二阶线性微分方程。…...

LSP的建立
MPLS需要为报文事先分配好标签,建立一条LSP,才能进行报文转发。LSP分为静态LSP和动态LSP两种。 静态LSP的建立 静态LSP是用户通过手工为各个转发等价类分配标签而建立的。由于静态LSP各节点上不能相互感知到整个LSP的情况,因此静态LSP是一个…...

huggingface的数据集下载(linux下clone)
1. 安装lfs sudo apt-get install git-lfs 或者 apt-get install git-lfs 2. git lfs install git lfs install 3. git clone dataset包 第2,3步骤的截图如下:...

Java使用dom4j生成kml(xml)文件遇到No such namespace prefix: xxx is in scope on:问题解决
介绍addAttribute和addNamepsace: addAttribute 方法 addAttribute 方法用于给XML元素添加属性。属性(Attributes)是元素的修饰符,提供了关于元素的额外信息,并且位于元素的开始标签中。属性通常用于指定元素的行为或样式&#…...

深入探讨Java中的LongAdder:使用技巧与避坑指南
文章目录 一、什么是LongAdder?二、LongAdder的简单使用示例代码: 三、LongAdder的工作原理四、LongAdder的常见使用场景五、使用LongAdder时的注意事项(避坑指南)1. 不要滥用LongAdder2. sum()方法与精度问题3. 避免过度使用rese…...

【本科毕业设计】基于单片机的智能家居防火防盗报警系统
基于单片机的智能家居防火防盗报警系统 相关资料链接下载摘要Abstract第1章 绪论1.1课题的背景1.2 研究的目的和意义 第2章 系统总体方案设计2.1 设计要求2.2 方案选择和论证2.2.1 单片机的选择2.2.2 显示方案的选择 第3章 系统硬件设计3.1 整体方案设计3.1.1 系统概述3.1.2 系…...

C语言 动态数据结构的C语言实现单向链表-2
建立一个单向链表 在单向链表中查找节点---查找尾节点 在单向链表中查找节点 --- 查找第 n 个节点 向单向链表中插入一个节点 向单向链表的尾部插入一个节点 向单向链表中某节点后插入一个节点 向单向链表中插入一个节点 删除单向链表中的某一节点 链表 vs 数组 动态数据结构...

Github 2024-10-23C开源项目日报 Top10
根据Github Trendings的统计,今日(2024-10-23统计)共有10个项目上榜。根据开发语言中项目的数量,汇总情况如下: 开发语言项目数量C项目10PLpgSQL项目1Redis - 内存数据库和数据结构服务器 创建周期:5411 天开发语言:C协议类型:BSD 3-Clause “New” or “Revised” Licen…...
: relocation报错解决)
ubuntu20.04 opencv4.0 /usr/local/lib/libgflags.a(gflags.cc.o): relocation报错解决
在一个只有ubuntu20.04的docker环境中配置opencv4.0.0, 什么库都没有,都要重新安装, 其他的问题在网上都找到了解决方案,唯独这个问题比较棘手: [ 86%] Linking CXX executable …/…/bin/opencv_annotation /usr/bin/ld: /usr/lo…...
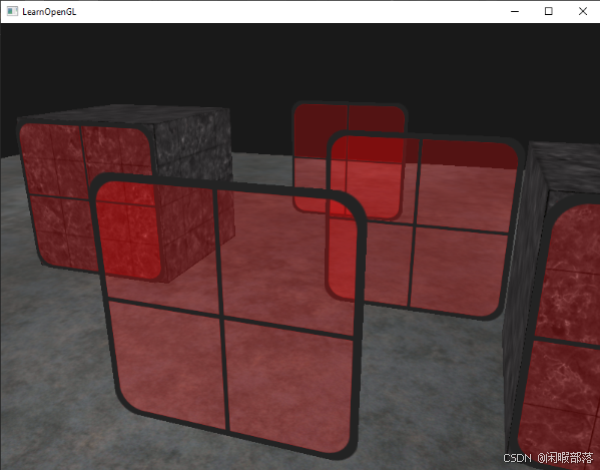
android openGL ES详解——混合
一、混合概念 混合是一种常用的技巧,通常可以用来实现半透明。但其实它也是十分灵活的,你可以通过不同的设置得到不同的混合结果,产生一些有趣或者奇怪的图象。混合是什么呢?混合就是把两种颜色混在一起。具体一点,就…...

计网--物理层
目录 物理层的任务 1、常见概念 2、信道极限容量 3、传输介质 (1)导引型传输介质 (2)非导引型传输介质 4、信道复用技术 (1)频分 / 时分 复用 (2)波分复用WDM (…...

算法的学习笔记—数组中的逆序对(牛客JZ51)
😀前言 在算法和数据结构领域,"逆序对"是一个经典问题。它在数组中两个数字之间定义,若前面的数字大于后面的数字,则这两个数字组成一个逆序对。我们要做的就是,给定一个数组,找出数组中所有的逆…...

Golang | Leetcode Golang题解之第498题对角线遍历
题目: 题解: func findDiagonalOrder(mat [][]int) []int {m, n : len(mat), len(mat[0])ans : make([]int, 0, m*n)for i : 0; i < mn-1; i {if i%2 1 {x : max(i-n1, 0)y : min(i, n-1)for x < m && y > 0 {ans append(ans, mat[x…...

什么是全局污染?怎么避免全局污染?
全局污染(Global Pollution)是指在编程过程中,过度使用全局变量或对象导致命名冲突、代码可维护性下降及潜在错误增加的问题。在 JavaScript 等动态语言中,尤其需要关注全局污染的风险。 全局污染的影响 1. 命名冲突 3. 意外修改…...

C# 串口通信教程
串口通信(Serial Communication)是一种用于设备之间数据传输的常见方法,通常用于与外部硬件设备(如传感器、机器人、微控制器)进行通信。在 C# 中,System.IO.Ports 命名空间提供了与串口设备交互的功能&…...

PHP编程基础
PHP(Hypertext Preprocessor,超文本预处理器)是一种广泛使用的开源服务器端脚本语言,主要用于网页开发,同时也可以进行命令行脚本编写。以下是PHP编程的基础知识: 1. PHP文件结构 PHP文件通常以 .php 为扩…...

TwinCAT3下位机配置EAP通讯传递与接收变量
添加EAP设备 DEVICE中右键选择添加新项,添加EAP(EtherCAT Automation Protocal)选择Network Variables类型,如下图。 设置网络适配器来激活EAP,在Adapter中选择search,选择网络适配器后确定,…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...
