WebGL编程指南 - 高级变换与动画基础
- 学习使用一个矩阵变换库,该库封装了矩阵运算的数学细节。
- 快速上手使用该矩阵库,对图形进行复合变换。
- 在该矩阵库的帮助下,实现简单的动画效果。
矩阵变换库:cuon-matrix.js
OpenGL中的函数:

书中 cuon-matrix.js 函数库中是这样实现的:
函数库主要创建了一个Matrix4类(构造函数),在该类原型函数下绑定了众多方法,许多函数之前都留有注释,我们主要看一下代码最前面的注释:
/** * This is a class treating 4x4 matrix.* This class contains the function that is equivalent to OpenGL matrix stack.* The matrix after conversion is calculated by multiplying a conversion matrix from the right.* The matrix is replaced by the calculated result.*/
根据注释可知,该函数库主要处理4×4的矩阵,对标OpenGL中矩阵处理函数。函数库提供了一个名为Matrix4的对象(构造函数),我们可以通过new方法创建它的实例,对象内部挂载了许多关于矩阵计算的方法。
这样使用函数库的方法,写起来更加简单
- 矩阵的创建方式:
// RotatedTriangle_Matrix.js
...// 创建旋转矩阵let radian = (Math.PI * ANGLE) / 180.0 // 转换为弧度制let cosB = Math.cos(radian)let sinB = Math.sin(radian)// 注意WebGL中矩阵是列主序的let xformMatrix = new Float32Array([cosB, sinB, 0.0, 0.0,-sinB, cosB, 0.0, 0.0,0.0, 0.0, 1.0, 0.0,0.0, 0.0, 0.0, 1.0,])...
// RotatedTriangle_Matrix4.js
...// 创建旋转矩阵// 为旋转矩阵创建Matrix4对象let xformMatrix = new Matrix4()// 将xformMatrix设置为旋转矩阵xformMatrix.setRotate(ANGLE, 0, 0, 1)
...
- 传输矩阵数据
// RotatedTriangle_Matrix.js
...// 将旋转图形所需数据传输给顶点着色器let u_xformMatrix = gl.getUniformLocation(gl.program, 'u_xformMatrix')if (!u_xformMatrix) {console.log('Failed to get the storage location of u_xformMatrix')}gl.uniformMatrix4fv(u_xformMatrix, false, xformMatrix)
...
// RotatedTriangle_Matrix4.js
...let u_xformMatrix = gl.getUniformLocation(gl.program, 'u_xformMatrix')if (!u_xformMatrix) {console.log('Failed to get the storage location of u_xformMatrix')}gl.uniformMatrix4fv(u_xformMatrix, false, xformMatrix.elements)
...


Matrix4在不提供数据直接初始化的情况下,其挂载的element元素就是一个单位阵,之后大部分操作都是对element元素进行的。
从上表可见,Matrix4对象有两种方法:
- 一种方法的名称中含有前缀set,这一类方法会根据参数计算出变换矩阵,然后将变换矩阵写入自身;
- 另一种方法的名称中不含set前缀,这一类方法在计算出变换矩阵后,会将自身与计算出的变换矩阵相乘,最终结果写入Matrix4对象。
复合变换RotatedTranslatedTriangle.js
相关内容:采用Matirx4对象,运用矩阵乘法模拟符合变换。
相关函数:Matrix4.setRotate(), Matrix4.translate()注意:矩阵乘法的先后顺序与模型变换的先后顺序有关,不能随意变化(矩阵乘法不满足乘法交换律)。

注意是 左乘

一个模型可能经过了多次变换,将这些变换全部复合成一个等效的变换,就得到了模型变换(model transformation),或称建模变换(modeling transformation),相应的,模型变换的矩阵称为模型矩阵(model matrix)。
重写Rotatedtriangle_Matrix4 代码:
- 命名习惯,在顶点着色器中命名uniform变量(mat4)为u_ModelMatrix,取模型矩阵之意。
// 顶点着色器
var VSHADER_SOURCE ='attribute vec4 a_Position;\n' +'uniform mat4 u_ModelMatrix;\n' +'void main(){\n' +' gl_Position = u_ModelMatrix * a_Position;\n' +'}\n'
- 构建矩阵时,采用Matrix4对象,先设置对象为旋转矩阵,再和平移矩阵相乘。
// 创建Matrix4对象let modelMatrix = new Matrix4()// 旋转角度let ANGLE = 90.0// 平移距离let Tx = 0.5// 设置模型矩阵为旋转矩阵modelMatrix.setRotate(ANGLE, 0, 0, 1)// 将模型矩阵乘以平移矩阵modelMatrix.translate(Tx, 0, 0)// 将模型矩阵传输给顶点着色器let u_ModelMatrix = gl.getUniformLocation(gl.program, 'u_ModelMatrix')if (!u_ModelMatrix) {console.log('Failed to get the storage location of u_ModelMatrix')}gl.uniformMatrix4fv(u_ModelMatrix, false, modelMatrix.elements)
完整代码:
// RotatedTranslatedTriangle.js
// 顶点着色器
var VSHADER_SOURCE ='attribute vec4 a_Position;\n' +'uniform mat4 u_ModelMatrix;\n' +'void main(){\n' +' gl_Position = u_ModelMatrix * a_Position;\n' +'}\n'
// 片元着色器
var FSHADER_SOURCE ='void main(){\n' + ' gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);\n' + '}\n'// 主函数
function main() {// 获取canvas元素let canvas = document.getElementById('webgl')// 获取WebGL上下文let gl = getWebGLContext(canvas)if (!gl) {console.log('Failed to get the rendering context for WebGL')return}// 初始化着色器if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {console.log('Failed to initialize shaders')return}// 设置顶点位置let n = initVertexBuffers(gl)if (n < 0) {console.log('Failed to set the positions of the vertices')return}// 创建Matrix4对象let modelMatrix = new Matrix4()// 旋转角度let ANGLE = 90.0// 平移距离let Tx = 0.5// 设置模型矩阵为旋转矩阵modelMatrix.setRotate(ANGLE, 0, 0, 1)// 将模型矩阵乘以平移矩阵modelMatrix.translate(Tx, 0, 0)// 将模型矩阵传输给顶点着色器let u_ModelMatrix = gl.getUniformLocation(gl.program, 'u_ModelMatrix')if (!u_ModelMatrix) {console.log('Failed to get the storage location of u_ModelMatrix')}gl.uniformMatrix4fv(u_ModelMatrix, false, modelMatrix.elements)// 设置背景色gl.clearColor(0.0, 0.0, 0.0, 1.0)// 清空绘图区gl.clear(gl.COLOR_BUFFER_BIT)// 绘制三角形gl.drawArrays(gl.TRIANGLES, 0, n)
}function initVertexBuffers(gl) {// 设置类型化数组和顶点数let vertices = new Float32Array([0.0, 0.3, -0.3, -0.3, 0.3, -0.3])let n = 3// 创建缓冲区对象let vertexBuffer = gl.createBuffer()if (!vertexBuffer) {console.log('Failed to create the buffer object')return -1}// 绑定缓冲区gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer)// 缓冲区写入数据gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STREAM_DRAW)let a_Position = gl.getAttribLocation(gl.program, 'a_Position')if (a_Position < 0) {console.log('Failed to get the storage location of a_Position')return -1}// 将缓冲区分配给attribute变量gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0)// 开启attribute变量(连接)gl.enableVertexAttribArray(a_Position)return n
}
动画-RotatingTriangle.js
相关内容:通过JavaScript灵活设计WebGL系统,通过反复变换和重绘图形生成动画效果;setInterval()系列函数和requestAnimationgFrame()系列函数的异同。
相关函数:setInterval(), requestAnimationFrame(), cancelAnimationFrame()
机制一:在t0、t1、t2、t3等时刻反复调用同一个函数来绘制三角形。
机制二:每次绘制之前,清除上次绘制的内容,并使三角形旋转相应的角度。
基于此,该实例程序与前面的示例有以下三点区别:
- 实现反复调用绘制函数的机制(机制一)
- 定义绘制函数,在绘制函数中包括清空绘图区、向着色器传值、绘制三步
- 由于程序需要反复绘制,所以在一开始就指定了背景色。
// RotatedTranslatedTriangle.js
// 顶点着色器
var VSHADER_SOURCE ='attribute vec4 a_Position;\n' +'uniform mat4 u_ModelMatrix;\n' +'void main(){\n' +' gl_Position = u_ModelMatrix * a_Position;\n' +'}\n'
// 片元着色器
var FSHADER_SOURCE ='void main(){\n' + ' gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0);\n' + '}\n'
// 旋转速度(度/秒)
var ANGLE_STEP = 45.0// 主函数
function main() {// 获取canvas元素let canvas = document.getElementById('webgl')// 获取WebGL上下文let gl = getWebGLContext(canvas)if (!gl) {console.log('Failed to get the rendering context for WebGL')return}// 初始化着色器if (!initShaders(gl, VSHADER_SOURCE, FSHADER_SOURCE)) {console.log('Failed to initialize shaders')return}// 设置顶点位置let n = initVertexBuffers(gl)if (n < 0) {console.log('Failed to set the positions of the vertices')return}// 设置背景色gl.clearColor(0.0, 0.0, 0.0, 1.0)// 获取u_ModelMatrix变量存储位置let u_ModelMatrix = gl.getUniformLocation(gl.program, 'u_ModelMatrix')if (!u_ModelMatrix) {console.log('Failed to get the storage location of u_ModelMatrix')}// 三角形当前旋转角度let currentAngle = 0.0// 模型矩阵,Matrix4对象let modelMatrix = new Matrix4()// 开始绘制三角形let tick = function () {currentAngle = animate(currentAngle) // 更新旋转角draw(gl, n, currentAngle, modelMatrix, u_ModelMatrix)requestAnimationFrame(tick) // 请求浏览器调用tick}tick()
}function initVertexBuffers(gl) {// 设置类型化数组和顶点数let vertices = new Float32Array([0.0, 0.3, -0.3, -0.3, 0.3, -0.3])let n = 3// 创建缓冲区对象let vertexBuffer = gl.createBuffer()if (!vertexBuffer) {console.log('Failed to create the buffer object')return -1}// 绑定缓冲区gl.bindBuffer(gl.ARRAY_BUFFER, vertexBuffer)// 缓冲区写入数据gl.bufferData(gl.ARRAY_BUFFER, vertices, gl.STREAM_DRAW)let a_Position = gl.getAttribLocation(gl.program, 'a_Position')if (a_Position < 0) {console.log('Failed to get the storage location of a_Position')return -1}// 将缓冲区分配给attribute变量gl.vertexAttribPointer(a_Position, 2, gl.FLOAT, false, 0, 0)// 开启attribute变量(连接)gl.enableVertexAttribArray(a_Position)return n
}
function draw(gl, n, currentAngle, modelMatrix, u_ModelMatrix) {// 设置旋转矩阵modelMatrix.setRotate(currentAngle, 0, 0, 1)// 旋转前加个平移// modelMatrix.translate(0.5, 0, 0)// 将旋转矩阵传输给顶点着色器gl.uniformMatrix4fv(u_ModelMatrix, false, modelMatrix.elements)// 清空绘图区gl.clear(gl.COLOR_BUFFER_BIT)// 绘制三角形gl.drawArrays(gl.TRIANGLES, 0, n)
}// 记录上一次调用函数的时刻
var g_last = Date.now()
// 更新旋转角
function animate(angle) {// 计算距离上次调用经过多长时间let now = Date.now()let elapsed = now - g_last // 毫秒g_last = now// 根据上次调用的时间,更新当前旋转角度let newAngle = angle + (ANGLE_STEP * elapsed) / 1000.0return (newAngle %= 360)
}


重复调用函数的方法:
// 开始绘制三角形let tick = function () {currentAngle = animate(currentAngle) // 更新旋转角draw(gl, n, currentAngle, modelMatrix, u_ModelMatrix) // 绘制三角形requestAnimationFrame(tick) // 请求浏览器调用tick}tick()

该方法是一个诞生较早的方法,其出现时浏览器还没有支持多标签页,所以在现代浏览器中,不论标签页是否被激活,该方法都会反复调用func,如果标签页较多,就会增加浏览器的负荷。

这一方法只有当标签页处于激活状态时才会生效,基于此也无法指定重复调用的时间间隔。

更新旋转角度:
...
// 旋转速度(度/秒)
var ANGLE_STEP = 45.0
...
// 记录上一次调用函数的时刻
var g_last = Date.now()
// 更新旋转角
function animate(angle) {// 计算距离上次调用经过多长时间let now = Date.now()let elapsed = now - g_last // 毫秒g_last = now// 根据上次调用的时间,更新当前旋转角度let newAngle = angle + (ANGLE_STEP * elapsed) / 1000.0return (newAngle %= 360)
}
animate()是更新旋转角的主要部分,该函数配合当前旋转角currentAngle变量、全局变量ANGLE_STEP变量(旋转速度)和g_last(上一次调用函数的时刻)使用,基本思路是:根据本次调用与上次调用之间的时间间隔来决定这一帧的旋转角度比上一帧大出多少
绘制函数的设计:
/*** 绘制三角形* @param {WebGLRenderingContext} gl 上下文对象* @param {number} n 顶点数量 int* @param {number} currentAngle 当前旋转角度 float* @param {Martix4} modelMatrix 根据当前的旋转角度计算出的旋转矩阵,存储在Martix4对象中* @param {number} u_ModelMatrix 顶点着色器中同名的uniform变量的存储位置 uint*/
function draw(gl, n, currentAngle, modelMatrix, u_ModelMatrix) {// 设置旋转矩阵modelMatrix.setRotate(currentAngle, 0, 0, 1)// 将旋转矩阵传输给顶点着色器gl.uniformMatrix4fv(u_ModelMatrix, false, modelMatrix.elements)// 清空绘图区gl.clear(gl.COLOR_BUFFER_BIT)// 绘制三角形gl.drawArrays(gl.TRIANGLES, 0, n)
}
参考:【《WebGL编程指南》读书笔记-高级变换与动画基础】_webgl高级-CSDN博客
相关文章:

WebGL编程指南 - 高级变换与动画基础
学习使用一个矩阵变换库,该库封装了矩阵运算的数学细节。快速上手使用该矩阵库,对图形进行复合变换。在该矩阵库的帮助下,实现简单的动画效果。 矩阵变换库:cuon-matrix.js OpenGL中的函数: 书中 cuon-matrix.js 函数…...

银行客户贷款行为数据挖掘与分析
#1024程序员节 | 征文# 在新时代下,消费者的需求结构、内容与方式发生巨大改变,企业要想获取更多竞争优势,需要借助大数据技术持续创新。本文分析了传统商业银行面临的挑战,并基于knn、逻辑回归、人工神经网络三种算法࿰…...

制程质量管理方案设计
质量管理系统框架——QMS 涵盖产生产制造体系的全生命周期的质量管理过程 与SAP、WMS、MES、OA等业务系统进行集成,整合各业务系统中的质量信息 利用整合的全价值链质量信息,寻找质量改进点和质量创新点 系统功能模块管理 系统管理:用户管理…...

uniapp移动端优惠券! 附源码!!!!
本文为常见的移动端uniapp优惠券,共有6种优惠券样式(参考了常见的优惠券),文本内容仅为示例,您可在此基础上调整为你想要的文本 预览效果 通过模拟数据,实现点击使用优惠券让其变为灰色的效果(模…...

【分布式技术】中间件-zookeeper安装配置
文章目录 安装部署1. 安装ZooKeeper2. 配置ZooKeeper3. 启动ZooKeeper服务器4. 使用ZooKeeper命令行客户端5. 使用ZooKeeper的四个基本操作6. ZooKeeper集群模式7. 安全和权限8. 监控和日志 相关文献 安装部署 在Linux环境中操作ZooKeeper通常涉及以下几个方面: 1…...

高等数学 7.6高阶线性微分方程
文章目录 一、线性微分方程的解的结构*二、常数变易法 方程 d 2 y d x 2 P ( x ) d y d x Q ( x ) f ( x ) (1) \cfrac{\mathrm{d}^2 y}{\mathrm{d}x^2} P(x) \cfrac{\mathrm{d}y}{\mathrm{d}x} Q(x) f(x) \tag{1} dx2d2yP(x)dxdyQ(x)f(x)(1) 叫做二阶线性微分方程。…...

LSP的建立
MPLS需要为报文事先分配好标签,建立一条LSP,才能进行报文转发。LSP分为静态LSP和动态LSP两种。 静态LSP的建立 静态LSP是用户通过手工为各个转发等价类分配标签而建立的。由于静态LSP各节点上不能相互感知到整个LSP的情况,因此静态LSP是一个…...

huggingface的数据集下载(linux下clone)
1. 安装lfs sudo apt-get install git-lfs 或者 apt-get install git-lfs 2. git lfs install git lfs install 3. git clone dataset包 第2,3步骤的截图如下:...

Java使用dom4j生成kml(xml)文件遇到No such namespace prefix: xxx is in scope on:问题解决
介绍addAttribute和addNamepsace: addAttribute 方法 addAttribute 方法用于给XML元素添加属性。属性(Attributes)是元素的修饰符,提供了关于元素的额外信息,并且位于元素的开始标签中。属性通常用于指定元素的行为或样式&#…...

深入探讨Java中的LongAdder:使用技巧与避坑指南
文章目录 一、什么是LongAdder?二、LongAdder的简单使用示例代码: 三、LongAdder的工作原理四、LongAdder的常见使用场景五、使用LongAdder时的注意事项(避坑指南)1. 不要滥用LongAdder2. sum()方法与精度问题3. 避免过度使用rese…...

【本科毕业设计】基于单片机的智能家居防火防盗报警系统
基于单片机的智能家居防火防盗报警系统 相关资料链接下载摘要Abstract第1章 绪论1.1课题的背景1.2 研究的目的和意义 第2章 系统总体方案设计2.1 设计要求2.2 方案选择和论证2.2.1 单片机的选择2.2.2 显示方案的选择 第3章 系统硬件设计3.1 整体方案设计3.1.1 系统概述3.1.2 系…...

C语言 动态数据结构的C语言实现单向链表-2
建立一个单向链表 在单向链表中查找节点---查找尾节点 在单向链表中查找节点 --- 查找第 n 个节点 向单向链表中插入一个节点 向单向链表的尾部插入一个节点 向单向链表中某节点后插入一个节点 向单向链表中插入一个节点 删除单向链表中的某一节点 链表 vs 数组 动态数据结构...

Github 2024-10-23C开源项目日报 Top10
根据Github Trendings的统计,今日(2024-10-23统计)共有10个项目上榜。根据开发语言中项目的数量,汇总情况如下: 开发语言项目数量C项目10PLpgSQL项目1Redis - 内存数据库和数据结构服务器 创建周期:5411 天开发语言:C协议类型:BSD 3-Clause “New” or “Revised” Licen…...
: relocation报错解决)
ubuntu20.04 opencv4.0 /usr/local/lib/libgflags.a(gflags.cc.o): relocation报错解决
在一个只有ubuntu20.04的docker环境中配置opencv4.0.0, 什么库都没有,都要重新安装, 其他的问题在网上都找到了解决方案,唯独这个问题比较棘手: [ 86%] Linking CXX executable …/…/bin/opencv_annotation /usr/bin/ld: /usr/lo…...
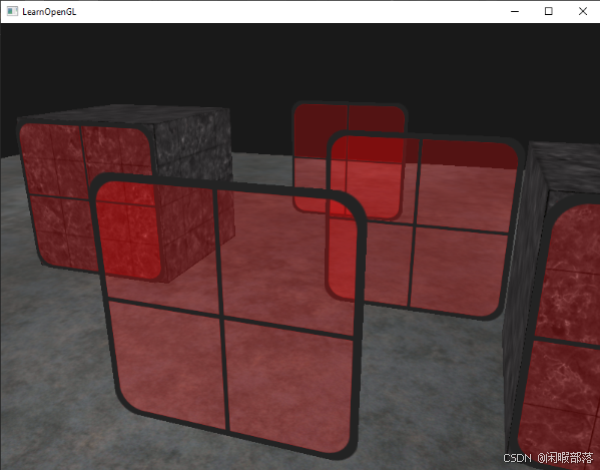
android openGL ES详解——混合
一、混合概念 混合是一种常用的技巧,通常可以用来实现半透明。但其实它也是十分灵活的,你可以通过不同的设置得到不同的混合结果,产生一些有趣或者奇怪的图象。混合是什么呢?混合就是把两种颜色混在一起。具体一点,就…...

计网--物理层
目录 物理层的任务 1、常见概念 2、信道极限容量 3、传输介质 (1)导引型传输介质 (2)非导引型传输介质 4、信道复用技术 (1)频分 / 时分 复用 (2)波分复用WDM (…...

算法的学习笔记—数组中的逆序对(牛客JZ51)
😀前言 在算法和数据结构领域,"逆序对"是一个经典问题。它在数组中两个数字之间定义,若前面的数字大于后面的数字,则这两个数字组成一个逆序对。我们要做的就是,给定一个数组,找出数组中所有的逆…...

Golang | Leetcode Golang题解之第498题对角线遍历
题目: 题解: func findDiagonalOrder(mat [][]int) []int {m, n : len(mat), len(mat[0])ans : make([]int, 0, m*n)for i : 0; i < mn-1; i {if i%2 1 {x : max(i-n1, 0)y : min(i, n-1)for x < m && y > 0 {ans append(ans, mat[x…...

什么是全局污染?怎么避免全局污染?
全局污染(Global Pollution)是指在编程过程中,过度使用全局变量或对象导致命名冲突、代码可维护性下降及潜在错误增加的问题。在 JavaScript 等动态语言中,尤其需要关注全局污染的风险。 全局污染的影响 1. 命名冲突 3. 意外修改…...

C# 串口通信教程
串口通信(Serial Communication)是一种用于设备之间数据传输的常见方法,通常用于与外部硬件设备(如传感器、机器人、微控制器)进行通信。在 C# 中,System.IO.Ports 命名空间提供了与串口设备交互的功能&…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10+pip3.10)
第一篇:Liunx环境下搭建PaddlePaddle 3.0基础环境(Liunx Centos8.5安装Python3.10pip3.10) 一:前言二:安装编译依赖二:安装Python3.10三:安装PIP3.10四:安装Paddlepaddle基础框架4.1…...
