常用排序算法总结
内容目录
- 1. 选择类排序
- 1.1 直接选择排序
- 1.2 堆排序
- 2. 交换类排序
- 2.1 冒泡排序
- 2.2 快速排序
- 3. 插入类排序
- 3.1 直接插入排序
- 3.2 希尔排序
- 4. 其它排序
- 4.1 归并排序
- 4.2 基数排序/桶排序
排序


1. 选择类排序
选择类排序的特征是每次从待排序集合中选择出一个最大值或者最小值。
1.1 直接选择排序
原理:两层循环,外层循环标记从哪开始遍历待排序数组,内层循环标记当前正在比较的元素。每次内层循环选出一个最小值/最大值。
ADL代码:

复杂度:
1.2 堆排序
原理:堆排序在逻辑上使用完全二叉树的结构,分为大顶堆和小顶堆两类,即根结点为最大值的二叉树和根节点为最小值的二叉树。在物理结构上一般使用数组来实现完全二叉树。以大顶堆为例,对待排序数组进行排序主要需要完成两个操作:
- 在待排序数组上构造大顶堆。
- 从堆中取出最大值,并调整堆使其根节点仍然存储最大值。
可见,使用堆排序也是每次从待排序集合中选择一个最大或者最小值,因此其属于选择排序。

那么该如何实现堆排序的这两个操作呢?
答案是:需要一个Restore操作负责:在其左右子树均已经为合法的堆的情况下,将以R为根的二叉树重建为堆。
有了Restore操作之后,就可以完成初始化整个堆和从堆中选择最大值或者最小值的操作了:
- 初始化整个堆: 从结点floor(n/2)开始直到结点1依次遍历,对以每个结点为根的子树执行Restore操作。
- 从堆中选出一个最大值:将结点1与最后一个结点交换,堆的大小减一,对新的结点1执行Restore操作。
ADL代码:
算法Restore(R, f, e. R)
/*R是存储完全二叉树的数组,索引从1开始;f是子树根节点索引;e是R中元素数量*/
R1.[初始化当前需要对比的子树的根]i <- f.
R2.[与左右子结点对比]// R[i]的右子结点就是R[2 * i + 1]// 左子节点就是R[2 * i]WHILE i <= e / 2 DO(IF 2 * i + 1 <= e AND R[2 * i + 1] > R[2 * i]child <- 2 * i + 1.ELSE child <- 2 * i.IF R[child] > R[i] THEN(R[child] <-> R[i].i <- child.)ELSE(BREAK.))|算法HeapSort(R, n. R)
/**/
H1.[初始化堆]FOR i = n/2 TO 1 STEP -1 DO(Restore(R, i, n. R).)
H2.[堆排序]e <- n.FOR j = n TO 2 STEP -1 DO(R[1] <-> R[j].e <- e - 1.Restore(R, 1, e. R).)|
复杂度:时间复杂度O(nlogn)。空间复杂度O(1)。不稳定。
2. 交换类排序
2.1 冒泡排序
原理:两层循环,外层循环标记待排序数组的最后一个元素下标e,内层循环负责比较当前元素i与其下一个元素j:
- 如果i > j,交换i,j。
- 如果i <= j,什么都不做。
这样内层循环遍历到e,此时e一定存储的是从1到e中的最大元素。
ADL代码:

扩展:看一下对冒泡排序的改进p237。改变了最好情况下的时间复杂度。
复杂度:O(n2)。O(1)。稳定。
2.2 快速排序
原理:快速排序基于一种自顶向下分治的思想,步骤如下:
- 如果待排序数组为空或者只剩下一个元素,直接返回
- 从待排序数组中任意选取一个元素,将比这个元素小的元素交换到数组的左边,比这个元素大的元素交换到数组的右边,这样就得到了两个子数组。
- 分别对两个子数组进行以上操作。
可以看到,这个算法适合使用递归来实现。
算法的关键问题和步骤在于:如何高效的把小的元素交换到右边,把大的元素交换到左边?
决定算法时间复杂度的步骤是:如何从待排序数组中选择一个元素,使其尽量把原数组划分为等长的子数组?
扩展:看一下对快速排序的改进p244,使用随机数算法选取基准元素。
ADL代码:
算法Partition(R, m, n. j)
/*负责从子数组[Rm, Rn]中选择一个基准元素,并把比它小的元素交换到数组的右边,比它大的元素交换到数组的左边。*返回值j是基准元素的下标。*/
P1.[选取一个基准元素]base <- R[m].
P2.[交换]left <- m + 1. right <- n.WHILE left < right DO(IF (R[left] > base && R[right] < base) THEN(R[left] <-> R[right].left <- left + 1.right <- right - 1.) ELSE IF R[left] <= base THENleft <- left + 1.ELSEright <- right - 1.)
P3. [返回基准元素]IF R[left] > base(R[left - 1] <-> R[m].j <- left - 1.)ELSE(R[left] <-> R[m].j <- left.)|算法QSort(R, m, n. R)
Q1. [递归出口]
IF (m == n || m > n) RETURN.
Q2. [划分数组]Partition(R, m, n. j).
Q3. [递归]QSort(R, m, j - 1. R).Qsort(R, j + 1, n. R).|
复杂度:
3. 插入类排序
3.1 直接插入排序
原理:两层循环,第一层循环标记前k个已经排好序的元素的下一个元素i,第二层循环将i插入到前k个元素中,使前k+1个元素有序。
ADL代码:

复杂度:复杂O(n2),最好情况下下O(n)。空间O(1)
3.2 希尔排序
原理:直接插入排序的性能与待排序数组本身的**”有序度“高度相关,原数组越有序,时间复杂度就越接近O(n),原数组越无序,时间复杂度越接近O(n2)。特别是远距离的逆序对比近距离的逆序对会显著增加比较次数**。
例如,下面这个数组(2, 1)这个逆序对需要比较101次才能调整有序
[..., 0, 2, ...100个元素..., 1, ...]
而,下面这个数组(2, 1)这个逆序对只需要比较11次。
[..., 0, 2, ...10个元素..., 1, ...]
那么为了尽量减少原数组中远距离的逆序对,需要直接在大的步长的子数组中进行排序,
例如,假设原数组有1000个元素,那么可以先选取步长为100,将如下子数组单独进行直接插入排序:
// 这里 子数组中的数字是下标而非元素的值
[1, 101, 201, ..., 901],
[2, 102, 202, ..., 902],
[3, 103, 203, ..., 903],
...
[100, 200, 300, ..., 1000]
之后逐步减少步长,然后进行排序,直到最后步长为1:
[1, 2, 3, ..., 1000] // 退化为原始的直接插入排序
这样,最后原数组会完全有序。
ADL代码:

4. 其它排序
4.1 归并排序
原理:类似快速排序,归并排序也利用了分而治之的思想,但是它是自底向上分治。步骤如下:
- 如果待排序的数组为空或者大小为1,直接返回
- 将数组从中间分开,对两个子数组分别进行以上操作
- 这时两个子数组已经有序,对两个子数组进行归并,然后返回
ADL代码:
算法Merge(R, t, m, n. X)
/**/建立X。算法MSort(R, m, n. R)
/**/
M1.[递归出口]IF m == n OR m > n THENRETURN.
M2.[划分数组]mid <- (m + n) / 2.MSort(R, m, mid. R).Msort(R, mid + 1, n. R).
M3.[归并]Merge(R, m, mid, n. R).|时间复杂度:O(nlogn)
4.2 基数排序/桶排序
不常考,了解即可。可能考简答题。
相关文章:

常用排序算法总结
内容目录 1. 选择类排序 1.1 直接选择排序1.2 堆排序 2. 交换类排序 2.1 冒泡排序2.2 快速排序 3. 插入类排序 3.1 直接插入排序3.2 希尔排序 4. 其它排序 4.1 归并排序4.2 基数排序/桶排序 排序 1. 选择类排序 选择类排序的特征是每次从待排序集合中选择出一个最大值或者最…...

[项目详解][boost搜索引擎#2] 建立index | 安装分词工具cppjieba | 实现倒排索引
目录 编写建立索引的模块 Index 1. 设计节点 2.基本结构 3.(难点) 构建索引 1. 构建正排索引(BuildForwardIndex) 2.❗构建倒排索引 3.1 cppjieba分词工具的安装和使用 3.2 引入cppjieba到项目中 倒排索引代码 本篇文章,我们将继续项…...

R语言编程
一、R语言在机器学习中的优势 R语言是一种广泛用于统计分析和数据可视化的编程语言,在机器学习领域也有诸多优势。 丰富的包:R拥有大量专门用于机器学习的包。例如,caret包是一个功能强大的机器学习工具包,它提供了统一的接口来训练和评估多种机器学习模型,如线性回归、决…...

Mysql主主互备配置
在现有运行的mysql环境下,修改相关配置项,完成主主互备模式的部署。 下面的配置说明中设置的mysql互备对应服务器IP为: 192.168.1.6 192.168.1.7 先检查UUID 在mysql的数据目录下,检查主备mysql的uuid(如下的server-…...
)
如何预防数据打架?数据仓库如何保持指标数据一致性开发指南(持续更新)
大数据开发人员最经常遇到尴尬和麻烦的事是,指标开发好了,以为万事大吉了。被业务和运营发现这个指标在不同地方数据打架,显示不同的数值。为了保证指标数据一致性,要从整个开发流程做好。 目录 一、数据仓库架构规划 二、数据抽取与转换 三、数据存储管理 四、指标管…...

我谈Canny算子
在Canny算子的论文中,提出了好的边缘检测算子应满足三点:①检测错误率低——尽可能多地查找出图像中的实际边缘,边缘的误检率(将边缘识别为非边缘)低,且避免噪声产生虚假边缘(将非边缘识别为边缘…...

算法的学习笔记—平衡二叉树(牛客JZ79)
😀前言 在数据结构中,二叉树是一种重要的树形结构。平衡二叉树是一种特殊的二叉树,其特性是任何节点的左右子树高度差的绝对值不超过1。本文将介绍如何判断一棵给定的二叉树是否为平衡二叉树,重点关注算法的时间复杂度和空间复杂度…...

SSM学习day01 JS基础语法
一、JS基础语法 跟java有点像,但是不用注明数据类型 使用var去声明变量 特点1:var关键字声明变量,是为全局变量,作用域很大。在一个代码块中定义的变量,在其他代码块里也能使用 特点2:可以重复定义&#…...

kubeadm快速自动化部署k8s集群
目录 一、准备环境 二、安装docker--三台机器都操作 三、使用kubeadm部署Kubernetes 在所有节点安装kubeadm和kubelet、kubectl 配置启动kubelet(所有主机) master节点初始化 Mater重新完成初始化 执行Master初始化后的提示配置 配置使用网络插件 创建flannel网络 …...

解决JAVA使用@JsonProperty序列化出现字段重复问题(大写开头的字段重复序列化)
文章目录 引言I 解决方案方案1:使用JsonAutoDetect注解方案2:手动编写get方法,JsonProperty注解加到方法上。方案3:首字母改成小写的II 知识扩展:对象默认是怎样被序列化?引言 需求: JSON序列化时,使用@JsonProperty注解,将字段名序列化为首字母大写,兼容前端和第三方…...

分布式理论基础
文章目录 1、理论基础2、CAP定理1_一致性2_可用性3_分区容错性4_总结 3、BASE理论1_Basically Available(基本可用)2_Soft State(软状态)3_Eventually Consistent(最终一致性)4_总结 1、理论基础 在计算机…...
-- jacoco agent)
Java应用程序的测试覆盖率之设计与实现(二)-- jacoco agent
说在前面的话 要想获得测试覆盖率报告,第一步要做的是,采集覆盖率数据,并输入到tcp。 而本文便是介绍一种java应用程序部署下的推荐方式。 作为一种通用方案,首先不想对应用程序有所侵入,其次运维和管理方便。 正好,jacoco agent就是类似于pinpoint agent一样,都使用…...

【机器学习】13. 决策树
决策树的构造 策略:从上往下学习通过recursive divide-and-conquer process(递归分治过程) 首先选择最好的变量作为根节点,给每一个可能的变量值创造分支。然后将样本放进子集之中,从每个分支的节点拓展一个。最后&a…...
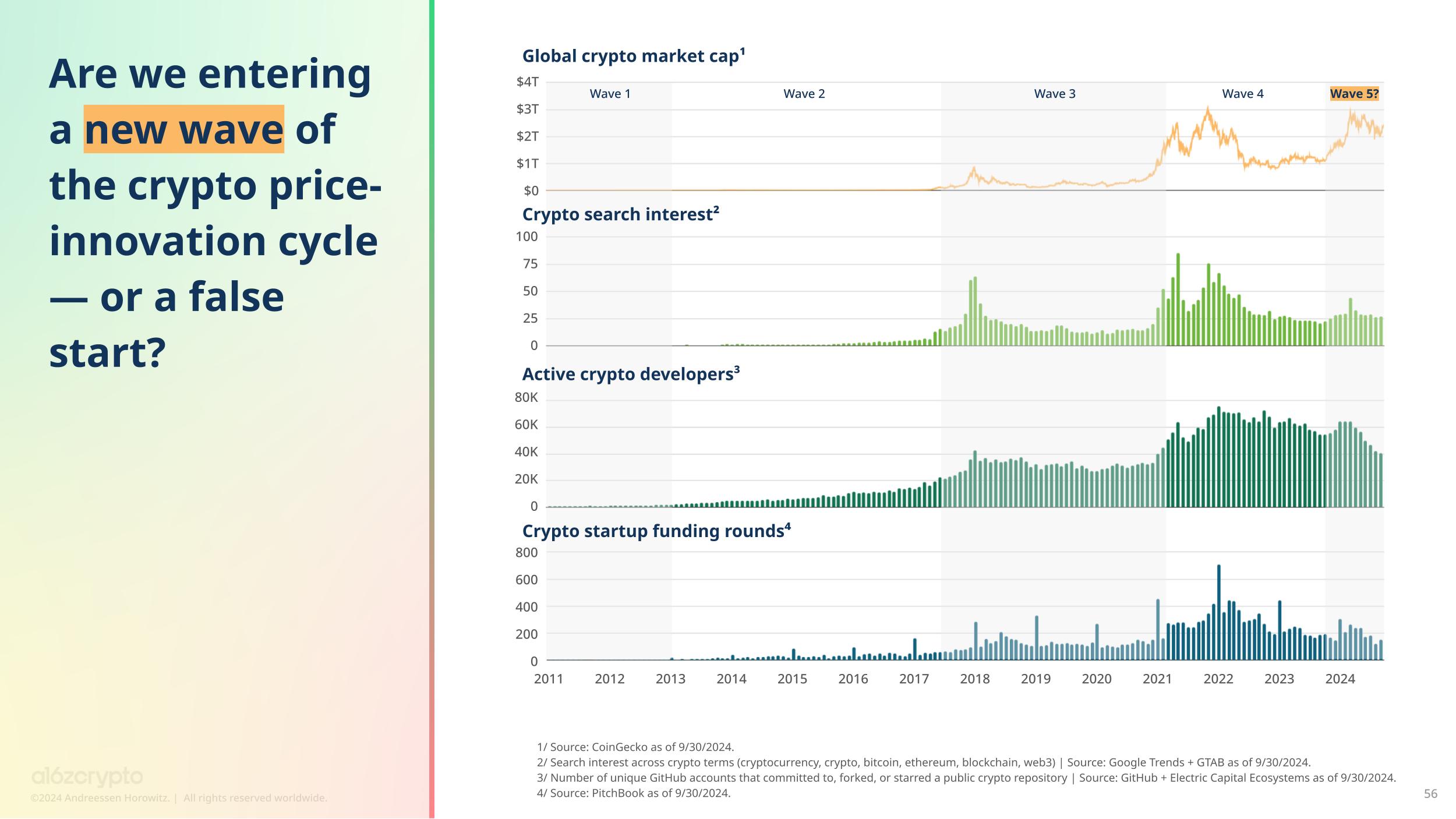
《a16z : 2024 年加密货币现状报告》解析
加密社 原文链接:State of Crypto 2024 - a16z crypto译者:AI翻译官,校对:翻译小组 当我们两年前第一次发布年度加密状态报告的时候,情况跟现在很不一样。那时候,加密货币还没成为政策制定者关心的大事。 比…...

Laravel 使用Simple QrCode 生成PNG遇到问题
最近因项目需求,需要对qrcode 进行一些简单修改,发现一些问题,顺便记录一下 目前最新的版本是4.2,在环境是 PHP8 ,laravel11 的版本默认下载基本是4.0以上的 如下列代码 QrCode::format(png)->generate(test);这样…...

一站式学习 Shell 脚本语法与编程技巧,踏出自动化的第一步
文章目录 1. 初识 Shell 解释器1.1 Shell 类型1.2 Shell 的父子关系 2. 编写第一个 Shell 脚本3. Shell 脚本语法3.1 脚本格式3.2 注释3.2.1 单行注释3.2.2 多行注释 3.3 Shell 变量3.3.1 系统预定义变量(环境变量)printenv 查看所有环境变量set 查看所有…...
批处理操作的优化
原来的代码 Override Transactional(rollbackFor Exception.class) public void batchAddQuestionsToBank(List<Long> questionIdList, Long questionBankId, User loginUser) {// 参数校验ThrowUtils.throwIf(CollUtil.isEmpty(questionIdList), ErrorCode.PARAMS_ERR…...

机器视觉运动控制一体机在DELTA并联机械手视觉上下料应用
市场应用背景 DELTA并联机械手是由三个相同的支链所组成,每个支链包含一个转动关节和一个移动关节,具有结构紧凑、占地面积小、高速高灵活性等特点,可在有限的空间内进行高效的作业,广泛应用于柔性上下料、包装、分拣、装配等需要…...

RHCE-web篇
一.web服务器 Web 服务器是一种软件或硬件系统,用于接收、处理和响应来自客户端(通常是浏览器)的 HTTP 请求。它的主要功能是存储和提供网站内容,比如 HTML 页面、图像、视频等。 Web 服务器的主要功能 处理请求…...

Java - 人工智能;SpringAI
一、人工智能(Artificial Intelligence,缩写为AI) 人工智能(Artificial Intelligence,缩写为AI)是一门新的技术科学,旨在开发、研究用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...
