【人工智能-初级】第6章 决策树和随机森林:浅显易懂的介绍及Python实践
文章目录
- 一、决策树简介
- 二、决策树的构建原理
- 2.1 决策树的优缺点
- 优点
- 缺点
- 三、随机森林简介
- 3.1 随机森林的构建过程
- 3.2 随机森林的优缺点
- 优点
- 缺点
- 四、Python实现决策树和随机森林
- 4.1 导入必要的库
- 4.2 加载数据集并进行预处理
- 4.3 创建决策树模型并进行训练
- 4.4 可视化决策树
- 4.5 创建随机森林模型并进行训练
- 4.6 模型预测与评估
- 五、总结
- 5.1 学习要点
- 5.2 练习题
一、决策树简介
决策树(Decision Tree)是一种树状结构的监督学习算法,可以用于分类和回归任务。它通过递归地将数据划分成不同的子集,直至每个子集只包含一个类别(对于分类问题)或达到某种特定的条件(对于回归问题)。
决策树非常直观,类似于人们在做决定时的思维过程。例如,在判断是否买房时,可能会依次考虑预算、房屋位置和是否满足个人需求等因素。决策树的结构由节点(node)和边(branch)组成,节点表示数据特征,边表示根据特征划分的数据路径。
二、决策树的构建原理
决策树的构建过程主要包括以下几步:
- 选择特征进行分裂:在每个节点,选择一个特征对数据进行划分,使得划分后的子集之间的纯度(或均匀度)尽可能高。
- 分裂节点:根据选择的特征将数据划分为两个或多个子集。
- 停止条件:递归地对每个子集构建子节点,直至满足停止条件(如树的最大深度,或节点中的样本数小于某个阈值)。
在选择特征进行分裂时,通常会使用一些标准来衡量子集的纯度,包括:
-
基尼不纯度(Gini Impurity):用于衡量节点中样本的混杂程度,值越小表示节点越纯。
G = 1 − ∑ i = 1 k p i 2 G = 1 - \sum_{i=1}^{k} p_i^2 G=1−i=1∑kpi2
其中,p_i 表示第 i 类样本的比例。 -
信息增益(Information Gain):用于衡量使用某个特征划分后的不确定性减少的程度。
I G = H ( D ) − ∑ i = 1 m ∣ D i ∣ ∣ D ∣ H ( D i ) IG = H(D) - \sum_{i=1}^{m} \frac{|D_i|}{|D|} H(D_i) IG=H(D)−i=1∑m∣D∣∣Di∣H(Di)
其中,H(D) 表示数据集 D 的熵,|D_i| 表示划分后的子集 D_i 的大小。
2.1 决策树的优缺点
优点
- 易于理解:决策树的结构简单直观,可以将复杂的决策过程可视化。
- 适应性强:决策树能够处理数值型和类别型特征,并且对数据的预处理要求较低。
- 能够处理多类别问题:决策树可以自然地处理多类别的分类问题。
缺点
- 容易过拟合:当决策树的深度过大时,模型容易学习到数据中的噪声,导致过拟合。
- 对小数据变化敏感:由于决策树的每一次划分都会影响后续的结构,数据的轻微变化可能会导致决策树的结构发生较大变化。
三、随机森林简介
随机森林(Random Forest)是一种集成学习方法,通过结合多个决策树的预测结果来提高分类或回归的性能。它通过随机采样和特征选择来生成多个相互独立的决策树,并将这些决策树的输出通过投票(分类任务)或平均(回归任务)来得到最终的预测结果。
3.1 随机森林的构建过程
- 随机采样:从原始数据集中有放回地随机抽取样本,生成多个训练数据集,这一过程称为 Bagging(Bootstrap Aggregating)。
- 特征选择:在构建每棵决策树时,随机选择部分特征用于分裂节点,以保证每棵树的多样性。
- 集成决策:对于分类任务,通过投票的方式决定最终分类结果;对于回归任务,通过取平均值来得到最终预测结果。
3.2 随机森林的优缺点
优点
- 高准确率:由于随机森林结合了多个决策树,能够显著提高模型的准确率和鲁棒性。
- 防止过拟合:随机森林通过随机采样和特征选择,减少了单棵决策树可能出现的过拟合问题。
- 特征重要性:随机森林可以评估每个特征对分类结果的重要性,从而帮助理解数据。
缺点
- 计算复杂度高:构建和集成多个决策树需要较高的计算资源和时间。
- 不可解释性:相比单棵决策树,随机森林的结构更复杂,不容易进行可视化和解释。
四、Python实现决策树和随机森林
接下来我们通过Python来实现决策树和随机森林,使用 scikit-learn 库来帮助我们完成这一任务。
4.1 导入必要的库
首先,我们需要导入一些必要的库:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
- numpy:用于数值计算。
- matplotlib:用于数据可视化。
- sklearn.datasets:用于加载 Iris 数据集,这是一个经典的多分类数据集。
- train_test_split:用于将数据集拆分为训练集和测试集。
- DecisionTreeClassifier:用于创建决策树分类器。
- RandomForestClassifier:用于创建随机森林分类器。
- accuracy_score, confusion_matrix, classification_report:用于评估模型的性能。
4.2 加载数据集并进行预处理
我们使用 Iris 数据集,这是一个常用的多分类数据集,包含三类花(山鸢尾、变色鸢尾、维吉尼亚鸢尾),每类有50个样本。
# 加载Iris数据集
data = load_iris()
X = data.data
y = data.target# 将数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
- load_iris():加载Iris数据集,X 是特征矩阵,y 是标签。
- train_test_split:将数据集拆分为训练集和测试集,20%的数据用于测试。
4.3 创建决策树模型并进行训练
我们创建一个决策树分类器,并用训练集进行模型训练。
# 创建决策树分类器
dt = DecisionTreeClassifier(criterion='gini', max_depth=3, random_state=42)# 训练模型
dt.fit(X_train, y_train)
- DecisionTreeClassifier(criterion=‘gini’, max_depth=3):创建决策树分类器,使用基尼不纯度作为分裂标准,最大深度为3。
- dt.fit(X_train, y_train):用训练数据拟合决策树模型。
4.4 可视化决策树
为了更好地理解决策树的结构,我们可以使用 plot_tree 方法对其进行可视化。
# 可视化决策树
plt.figure(figsize=(12, 8))
plot_tree(dt, filled=True, feature_names=data.feature_names, class_names=data.target_names)
plt.show()
通过上述代码,我们可以看到决策树的结构,包括每个节点的特征、基尼不纯度、样本数量以及类别分布。
4.5 创建随机森林模型并进行训练
接下来,我们创建一个随机森林分类器,并用训练集进行模型训练。
# 创建随机森林分类器
rf = RandomForestClassifier(n_estimators=100, criterion='gini', random_state=42)# 训练模型
rf.fit(X_train, y_train)
- RandomForestClassifier(n_estimators=100, criterion=‘gini’):创建随机森林分类器,包含100棵决策树,使用基尼不纯度作为分裂标准。
- rf.fit(X_train, y_train):用训练数据拟合随机森林模型。
4.6 模型预测与评估
使用测试集对决策树和随机森林模型分别进行预测,并评估其性能。
# 决策树预测
y_pred_dt = dt.predict(X_test)
accuracy_dt = accuracy_score(y_test, y_pred_dt)
print(f"决策树模型的准确率: {accuracy_dt * 100:.2f}%")# 随机森林预测
y_pred_rf = rf.predict(X_test)
accuracy_rf = accuracy_score(y_test, y_pred_rf)
print(f"随机森林模型的准确率: {accuracy_rf * 100:.2f}%")
- dt.predict(X_test) 和 rf.predict(X_test):分别对测试集进行预测。
- accuracy_score:计算预测的准确率。
我们可以看到随机森林模型的准确率通常比单棵决策树要高,这是因为随机森林通过集成多个决策树的预测结果来提高模型的泛化能力。
五、总结
决策树是一种简单直观的监督学习算法,可以用于分类和回归任务。它通过递归地将数据划分成不同的子集,直至达到某种特定的条件。随机森林则是通过结合多个决策树来提高模型的性能,是一种强大的集成学习方法。
5.1 学习要点
- 决策树原理:决策树通过递归划分数据来建立分类或回归模型,使用基尼不纯度或信息增益来衡量划分的好坏。
- 随机森林原理:随机森林结合了多个决策树,通过随机采样和特征选择来提高模型的准确率和鲁棒性。
- Python实现:可以使用 scikit-learn 库中的 DecisionTreeClassifier 和 RandomForestClassifier 轻松实现决策树和随机森林。
5.2 练习题
- 使用决策树对 Iris 数据集进行回归任务,观察模型的表现。
- 使用 sklearn.datasets 模块中的 load_wine 数据集,构建一个随机森林分类模型,预测葡萄酒的类别。
- 尝试调整决策树和随机森林的参数,如树的最大深度、估计器数量等,观察模型的性能变化。
希望本文能帮助您更好地理解决策树和随机森林的基本概念和实现方法。下一篇文章将为您介绍K-Means聚类及其Python实现。如果有任何问题,欢迎在评论中讨论!
相关文章:

【人工智能-初级】第6章 决策树和随机森林:浅显易懂的介绍及Python实践
文章目录 一、决策树简介二、决策树的构建原理2.1 决策树的优缺点优点缺点 三、随机森林简介3.1 随机森林的构建过程3.2 随机森林的优缺点优点缺点 四、Python实现决策树和随机森林4.1 导入必要的库4.2 加载数据集并进行预处理4.3 创建决策树模型并进行训练4.4 可视化决策树4.5…...
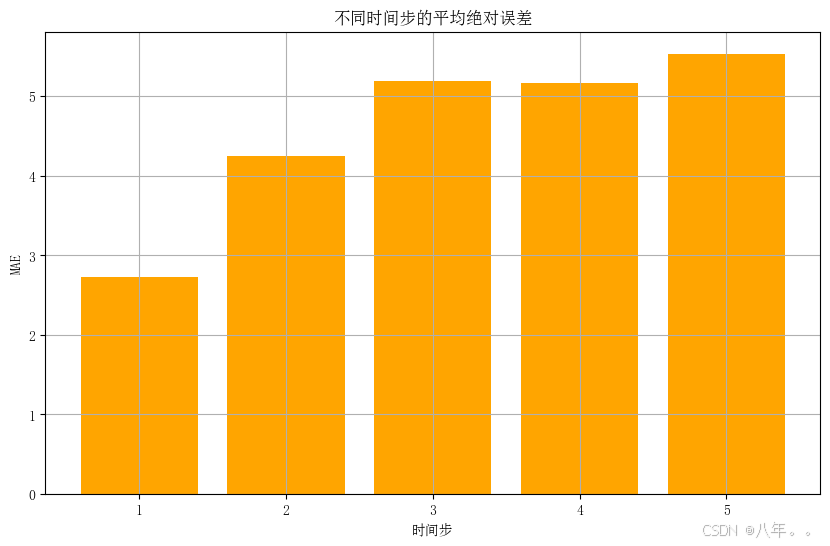
时间序列预测(九)——门控循环单元网络(GRU)
目录 一、GRU结构 二、GRU核心思想 1、更新门(Update Gate):决定了当前时刻隐藏状态中旧状态和新候选状态的混合比例。 2、重置门(Reset Gate):用于控制前一时刻隐藏状态对当前候选隐藏状态的影响程度。…...

李东生牵手通力股份IPO注册卡关,三年近10亿“清仓式分红”引关注
《港湾商业观察》施子夫 9月27日,通力科技股份有限公司(以下简称,通力股份)再度提交了注册申请,实际上早在去年11月6日公司已经提交过注册,看起来公司注册环节面临卡关。公开信息显示,通力股份…...

Android13、14特殊权限-应用安装权限适配
Android13、14特殊权限-应用安装权限适配 文章目录 Android13、14特殊权限-应用安装权限适配一、前言二、权限适配三、其他1、特殊权限-应用安装权限适配小结2、dumpsys package查看获取到了应用安装权限3、Android权限系统:应用操作管理类AppOpsManager(…...
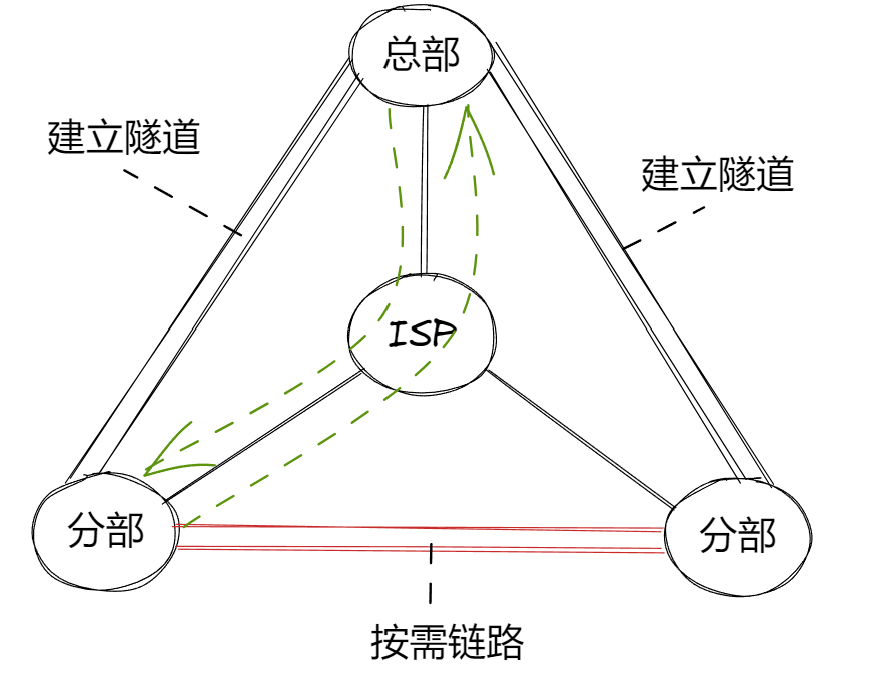
DMVPN协议
DMVPN(Dynamic Multipoint VPN)动态多点VPN 对于分公司和分总公司内网实现通信环境下,分公司是很多的。我们不可能每个分公司和总公司都挨个建立ipsec隧道 ,而且如果是分公司和分公司建立隧道,就会很麻烦。此时我们需…...
-零钱兑换II)
leetcode动态规划(十八)-零钱兑换II
题目 322.零钱兑换II 给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。 计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。 你可以认为每种硬…...

2024 CSP-J 题解
2024 CSP-J题解 扑克牌 题目给出了一整套牌的定义,但是纯粹在扯淡,完全没有必要去判断给出的牌的花色和点数,我们用一个循环来依次读入每一张牌,如果这个牌在之前出现过,我们就让答案减一。这里建议用map、unorde…...

GPU 服务器厂家:中国加速计算服务器市场的前瞻洞察
科技的飞速发展,让 GPU 服务器在加速计算服务器领域的地位愈发凸显。中国加速计算服务器市场正展现出蓬勃的生机,而 GPU 服务器厂家则是这场科技盛宴中的关键角色。 从市场预测的趋势来看,2023 年起,中国加速计算服务器市场便已展…...

Hadoop集群修改yarn队列
1.修改默认的default队列参数 注意: yarn.scheduler.capacity.root.队列名.capacity总和不能超过100 <property><name>yarn.scheduler.capacity.root.queues</name><value>default,hive,spark,flink</value><description>The…...

【GPIO】2.ADC配置错误,还是能得到电压数据
配置ADC功能时,GPIO引脚弄错了,P1写成P2,但还是配置成功,能得到电压数据。 首先一步步排查: 既然引脚弄错了,那引脚改为正确的引脚,能得到数据通过第一步判断,GPIO配置似乎是不起作…...

css-元素居中方式
<section class"wrapper"><div class"content">Content goes here</div> </section>1. 使用 Flexbox Flexbox 是一种现代的布局方法,可以轻松实现居中。 .wrapper {display: flex; /* 使用 Flexbox …...

redis内存打满了怎么办?
1、设置maxmemory的大小 我们需要给 Redis设置maxmemory的大小,如果不设置的话,它会受限于系统的物理内存和系统对内存的管理机制。 2、设置内存的淘汰策略 内存的淘汰策略分为 8 种,从淘汰范围来说分为从所有的key中淘汰和从设置过期时间…...

决策算法的技术分析
系列文章目录 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 TODO:写完再整理 文章目录 系列文章目录前言(1)第一层级:分层状态机、分层决策树的想法(三个臭皮匠胜过一个诸葛亮)基于场景的固定规则化的分层决策核心思想(2)第二层级:数据管理的方…...
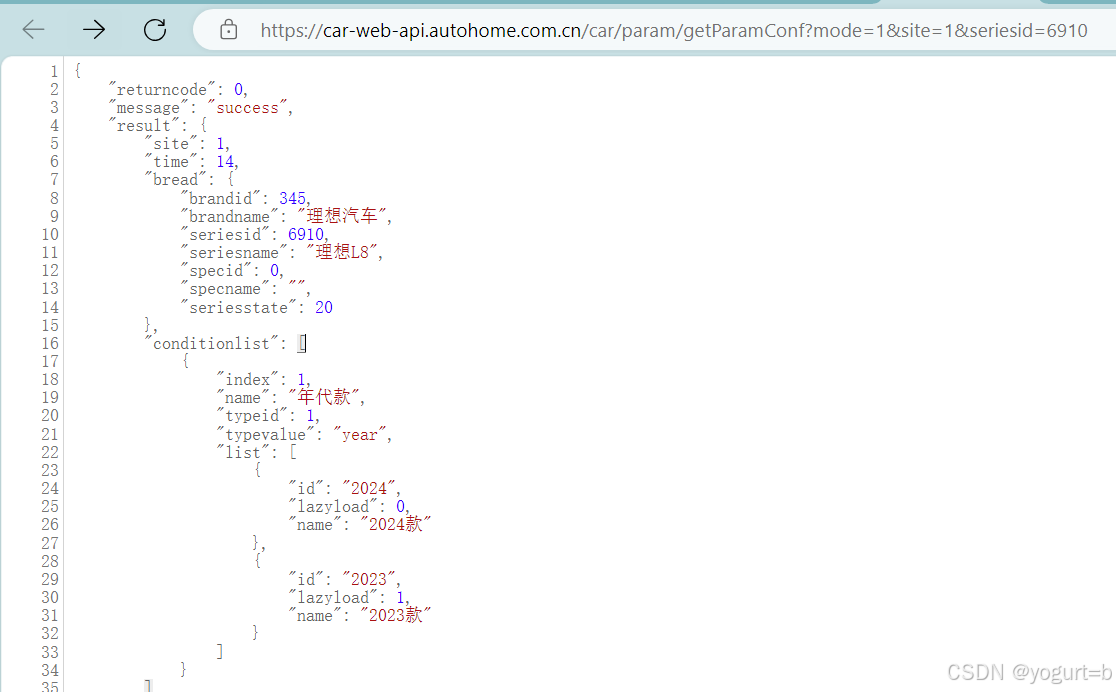
【Python爬虫】获取汽车之家车型配置附代码(2024.10)
参考大哥,感谢大哥:https://blog.csdn.net/weixin_43498642/article/details/136896338 【任务目标】 工作需要想更方便地下载汽车之家某车系配置清单;(垃圾汽车之家不给下载导出表格,配置页叉掉了车系要出来还要重新…...
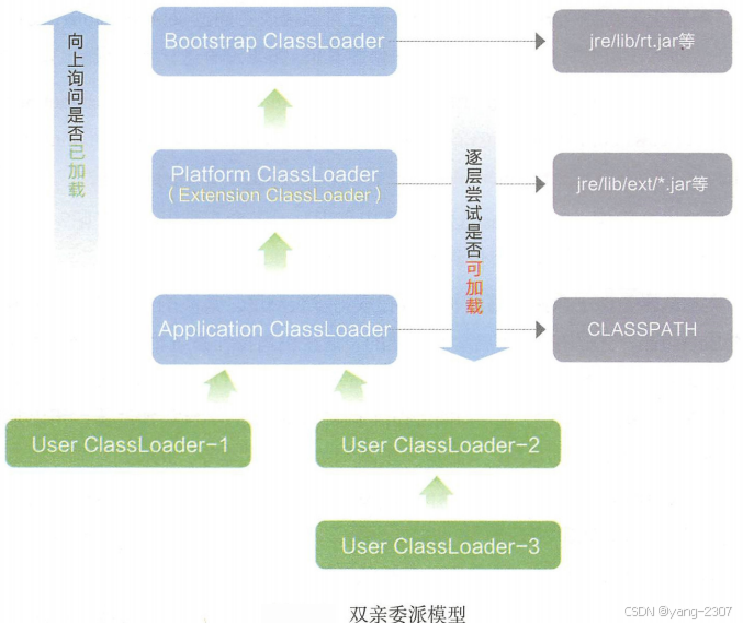
JVM 加载 class 文件的原理机制
JVM 加载 class 文件的原理机制 JVM(Java虚拟机)是一个可以执行Java字节码的虚拟机。它负责执行Java应用程序和应用程序的扩展,如Java库和框架。 文章目录 JVM 加载 class 文件的原理机制1. JVM1.1 类加载器1.2 魔数1.3 元空间 2. 类加载2.1 …...
NumPy学习第九课:字符串相关函数
前言 各位有没有注意到,NumPy从第八课开始其实基本上都是讲的是NumPy的函数,而且其实就是各种函数的调用,因为NumPy是一个很强大的函数库,这对我们以后再处理项目中遇到的问题时会有很大的帮助。我们将常用的函数进行一个列举&am…...
在处理光谱特征的序列属性时表现不佳)
卷积神经网络(CNNs)在处理光谱特征的序列属性时表现不佳
卷积神经网络(CNNs)在处理光谱签名的序列属性时表现不佳,主要是由于其固有网络架构的局限性。具体原因如下: 局部感受野(Local Receptive Field): CNN 的核心操作是卷积,它利用局部感…...

【IC】MCU的Tick和晶振频率
Tick 是指 MCU 内部时钟的一个周期,通常表示为一个固定的时间间隔。每个 tick 代表一个时间单位,通常以毫秒(ms)或微秒(μs)为单位。Tick 通常由 MCU 的定时器或计时器生成,作为系统时钟的一部分…...

从0到1学习node.js(npm)
文章目录 一、NPM的生产环境与开发环境二、全局安装三、npm安装指定版本的包四、删除包 五、用npm发布一个包六、修改和删除npm包1、修改2、删除 一、NPM的生产环境与开发环境 类型命令补充生产依赖npm i -S uniq-S 等效于 --save -S是默认选项npm i -save uniq包的信息保存在…...

【STM32 Blue Pill编程实例】-OLED显示DS18B20传感器数据
OLED显示DS18B20传感器数据 文章目录 OLED显示DS18B20传感器数据1、DS18B20介绍2、硬件准备及接线3、模块配置3.1 定时器配置3.2 DS18B20传感器配置3.3 OLED的I2C接口配置4、代码实现在本文中,我们将介绍如何将 DS18B20 温度传感器与 STM32 Blue Pill 开发板连接,并使用 HAL …...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

Python 训练营打卡 Day 47
注意力热力图可视化 在day 46代码的基础上,对比不同卷积层热力图可视化的结果 import torch import torch.nn as nn import torch.optim as optim from torchvision import datasets, transforms from torch.utils.data import DataLoader import matplotlib.pypl…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...
