2024 CSP-J 题解
2024 CSP-J题解
扑克牌
题目给出了一整套牌的定义,但是纯粹在扯淡,完全没有必要去判断给出的牌的花色和点数,我们用一个循环来依次读入每一张牌,如果这个牌在之前出现过,我们就让答案减一。这里建议用map、unordered_set或者给每一种牌一个编号,然后用数组存储也可以。
#include <bits/stdc++.h>using namespace std;int n;int main()
{map<string, bool> M;int ans = 52;cin >> n;for (int i = 1; i <= n; i++){string tmp;cin >> tmp;if (!M[tmp])ans--, M[tmp] = 1;}cout << ans;return 0;
}
地图探险
纯粹的记忆化搜索,用数组存储对于每一个方向下一步坐标的差值,每次要执行移动操作之前,我们都要不停地执行右转的操作,直到下一步的坐标合法为止。
我们可以开辟一个二维数组来记录每一次搜索经过的位置,每次走到一个之前没走过的位置,我们就让答案加一。
#include <bits/stdc++.h>using namespace std;const int maxn = 1e3 + 5;
int mx[4] = {0, 1, 0, -1}, my[4] = {1, 0, -1, 0}, ans; // mx 和 my 用来存储每一个方向对应的变化值
char Map[maxn][maxn]; // 储存整个地图
bool vis[maxn][maxn]; // 记录每个地方都有没有被遍历过
int n, m, k, x_0, y_0, d;void dfs(int x, int y, int d)
{if (!vis[x][y]) // 如果这个位置还没有走过,就让答案加一ans++;vis[x][y] = 1;int X = x + mx[d], Y = y + my[d]; // 下一步要走的位置while ((X < 1 || X > n || Y < 1 || Y > m || Map[X][Y] == 'x') && k) // 下一步不合法,并且还需要执行操作,那么我们右转d = (d + 1) % 4, k--, X = x + mx[d], Y = y + my[d]; // k 一定要减一if (k == 0) // 后面没有操作要进行了return;k--;dfs(X, Y, d); // 移动到下一步
}void solve()
{cin >> n >> m >> k;cin >> x_0 >> y_0 >> d;for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)cin >> Map[i][j];dfs(x_0, y_0, d);cout << ans << '\n'; // 因为多组样例,这几行都是清空的操作ans = 0;for (int i = 1; i <= n; i++)for (int j = 1; j <= m; j++)vis[i][j] = 0;
}int main()
{int T;cin >> T;while (T--){solve();}return 0;
}
小木棍
数学(dabiao)题,可以先简单找找规律。
首先对于 0~9 每一种数字,如果要用火柴拼出来的话,他们分别需要 6, 2, 5, 5, 4, 5, 6, 3, 7, 6 根木条。根据数据范围,我们可以得到一点提示,这题反正是跟 7 脱不了关系。
其次有一个很显而易见的道理,因为 8 这个数字需要的火柴最多,整个数字的长度就越短,也就越小,那么当 n 是 7 的倍数时,那么 ( n / 7 ) (n / 7) (n/7) 个 8 组成的数字就是最小的。
除此之外:
如果 n % 7 = 1:
因为一根火柴什么数字都拼不出来,所以需要去牺牲从前往后第二个数字来凑出一个数来(想不出来可以打表)。结果就是 10 + 很多个 8。
但是需要特判 n = 1 的时候,结果是 -1。
如果 n % 7 = 2:
两根火柴可以组成一个 1,后面全部填 8。
如果 n % 7 = 3:
需要特判 n = 3 和 n = 10,答案分别是 7 和 22,其他情况,答案是 200 + 很多个 8。
如果 n % 7 = 4:
特判 n = 4,答案是 4,其他情况答案是 20 + 很多个 8。
如果 n % 7 = 5:
结果是 2 + 很多个 8。
如果 n % 7 = 6:
结果是 6 + 很多个 8。
#include <bits/stdc++.h>using namespace std;int n, T;int main()
{cin >> T;while (T--){cin >> n;int type = n % 7;if (type == 0){for (int i = 1; i <= n / 7; i++)cout << 8;cout << '\n';continue;}if (type == 1){if (n == 1)cout << -1 << '\n';else{cout << 10;for (int i = 1; i <= n / 7 - 1; i++)cout << 8;cout << '\n';}continue;}if (type == 2){cout << 1;for (int i = 1; i <= n / 7; i++)cout << 8;cout << '\n';continue;}if (type == 3){if (n == 3)cout << 7 << '\n';else if (n == 10)cout << 22 << '\n';else{cout << 200;for (int i = 1; i <= (n - 17) / 7; i++)cout << 8;cout << '\n';}continue;}if (type == 4){if (n == 4)cout << 4 << '\n';else{cout << 20;for (int i = 1; i <= (n - 11) / 7; i++)cout << 8;cout << '\n';}continue;}if (type == 5){cout << 2;for (int i = 1; i <= (n - 5) / 7; i++)cout << 8;cout << '\n';continue;}if (type == 6){cout << 6;for (int i = 1; i <= (n - 6) / 7; i++)cout << 8;cout << '\n';continue;}}return 0;
}
这种题目一般建议还是先打个表找找规律,或者直接写一个暴力看看比较小的数据点的答案。例如这个题目,可以先写一个 10 的某次方的暴搜,枚举每一位是多少。
接龙
这里我没有想到特别简单的思路,要么就是空间不太正确,要么就是时间不太正确,目前的做法是 dp + 差分前缀和。
我们预处理出 100 轮每一轮的答案,然后做个离线的输出,我们把所有的询问按照从小到大的顺序进行排序,因为预处理的时候我们是按照轮数从小到大的顺序进行 d p dp dp 的,所以我们直接把答案全部记录下来就可以。
然后就是 d p dp dp 状态的设计,首先 d p [ i ] [ j ] dp[i][j] dp[i][j] 表示第 i 轮以元素 j 为结尾的答案。但是这里因为第 i 轮的答案只与前一轮有关,所以我们可以把 d p dp dp 的前一个状态去掉,用两个 d p dp dp 数组轮流使用就可以了。
因为在接龙的时候,当前这一轮的人不能和上一轮一样,所以我们重新设计一下状态, dp[j] 表示当前这一轮以元素 j 结尾。
d p [ j ] = − 2 dp[j] = -2 dp[j]=−2:当前这一轮以 j 结尾,没人能完成接龙;
d p [ j ] = − 1 dp[j] = -1 dp[j]=−1:当前这一轮以 j 结尾,有两个人能完成接龙,根据题意,如果有两个人能完成接龙(使用的句子开头和结尾相同),那么接龙就一定可以完成,所以我们只用考虑两个人的情况就可以了,两个人以上不用考虑;
d p [ j ] = i dp[j] = i dp[j]=i(i 大于 0):当前这一轮以 j 结尾,并且只有一个人能完成接龙,这个人的编号是 i i i。
状态转移方程:
对于每一个人 i 遍历所有的 S i , j S_{i,j} Si,j (第 i i i 个人的词库里面的第 j j j 个字符),当发现上一轮 d p [ S i , j ] dp[S_{i, j}] dp[Si,j] 不等于 − 2 -2 −2 且不等于 i i i 的时候(连续的两轮不能是同一个人),说明这个数后面的 k 个元素,可以在当前这一轮作为的最后一个元素完成接龙,因为是连续的一个区间,所以这里我们使用差分来进行维护,然后我们再进行前缀和,这样就可以看出来有哪些元素可以完成接龙了(对于 i i i 这一个人来说),把找出来的元素的 d p dp dp 值赋成 i i i。
然后我们再去处理其他人,如果发现有一个元素已经被赋值了,说明有两个或者两个以上的人可以使用这个元素作为结尾完成这一轮接龙, d p dp dp 值就是 -1。
#include <bits/stdc++.h>using namespace std;
using ll = long long;void solve()
{int n, k, q;cin >> n >> k >> q;vector<vector<int>> g(n); // 存储所有的 Svector<int> len(n); // 每个 S 对应的长度int maxn = -1;bool flag = false; // 如果没有 1,说明完全没有可能接龙,直接寄for (int i = 0; i < n; i += 1){cin >> len[i];g[i].resize(len[i]);for (int j = 0; j < len[i]; j += 1){cin >> g[i][j];maxn = max(maxn, g[i][j] + 1);if (g[i][j] == 1 && j != len[i] - 1)flag = true;}}vector<tuple<int, int, int>> a(q); // 储存询问int idx = 0, ma = 0;for (auto &[r, c, id] : a){cin >> r >> c;ma = max(ma, r);id = idx++;}idx = 0;sort(a.begin(), a.end()); // 按照轮数从小到大的顺序排列vector<int> ans(q); // 答案vector<int> dp(maxn, -2); // 先全部赋值成 -2,表示不能以 j 为结尾完成这一轮dp[1] = -1;vector<int> now(200000); // 差分数组for (int round = 1; round <= ma && flag; round += 1){vector<int> dp1(maxn, -2); // 当前这一轮的 dp 值for (int i = 0; i < n; i += 1) // 枚举第几个人{for (int j = 0; j < len[i]; j++) // 初始化now[j] = 0;for (int j = 0; j < len[i] - 1; j += 1) {int x = g[i][j];if (dp[x] != -2 && dp[x] != i) // dp 是上一轮的结果,如果 x 可以作为接龙的结尾,那么后面 k 个也可以 {int to = j + k; // 差分now[j + 1] += 1;if (to < len[i])now[to] -= 1;}}for (int j = 1; j < len[i]; j += 1){int x = g[i][j];now[j] += now[j - 1]; // 前缀和if (now[j] != 0 && dp1[x] != -1) // 如果这个数字被差分标记了并且没有两个以上的人标记了这个元素(如果是 -1 就不用管了){if (dp1[x] == -2)dp1[x] = i;else if (dp1[x] != i) // 已经有别人标记过了dp1[x] = -1;}}}while (idx < q) // 给每一个询问提供一个答案{auto &[r, c, id] = a[idx];if (r != round)break;else{if (c >= maxn || dp1[c] == -2)ans[id] = 0;elseans[id] = 1;idx += 1;}}dp = dp1;}for (int i = 0; i < q; i += 1) // 离线输出结果cout << ans[i] << "\n";
}
int main()
{ ios::sync_with_stdio(0); // 怕被卡,关流一下 cin.tie(0);int t;cin >> t;while (t--){solve();}return 0;
}
作者能力有限,如果有任何错误之处,还请各位指教。
相关文章:

2024 CSP-J 题解
2024 CSP-J题解 扑克牌 题目给出了一整套牌的定义,但是纯粹在扯淡,完全没有必要去判断给出的牌的花色和点数,我们用一个循环来依次读入每一张牌,如果这个牌在之前出现过,我们就让答案减一。这里建议用map、unorde…...

GPU 服务器厂家:中国加速计算服务器市场的前瞻洞察
科技的飞速发展,让 GPU 服务器在加速计算服务器领域的地位愈发凸显。中国加速计算服务器市场正展现出蓬勃的生机,而 GPU 服务器厂家则是这场科技盛宴中的关键角色。 从市场预测的趋势来看,2023 年起,中国加速计算服务器市场便已展…...

Hadoop集群修改yarn队列
1.修改默认的default队列参数 注意: yarn.scheduler.capacity.root.队列名.capacity总和不能超过100 <property><name>yarn.scheduler.capacity.root.queues</name><value>default,hive,spark,flink</value><description>The…...

【GPIO】2.ADC配置错误,还是能得到电压数据
配置ADC功能时,GPIO引脚弄错了,P1写成P2,但还是配置成功,能得到电压数据。 首先一步步排查: 既然引脚弄错了,那引脚改为正确的引脚,能得到数据通过第一步判断,GPIO配置似乎是不起作…...

css-元素居中方式
<section class"wrapper"><div class"content">Content goes here</div> </section>1. 使用 Flexbox Flexbox 是一种现代的布局方法,可以轻松实现居中。 .wrapper {display: flex; /* 使用 Flexbox …...

redis内存打满了怎么办?
1、设置maxmemory的大小 我们需要给 Redis设置maxmemory的大小,如果不设置的话,它会受限于系统的物理内存和系统对内存的管理机制。 2、设置内存的淘汰策略 内存的淘汰策略分为 8 种,从淘汰范围来说分为从所有的key中淘汰和从设置过期时间…...

决策算法的技术分析
系列文章目录 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 TODO:写完再整理 文章目录 系列文章目录前言(1)第一层级:分层状态机、分层决策树的想法(三个臭皮匠胜过一个诸葛亮)基于场景的固定规则化的分层决策核心思想(2)第二层级:数据管理的方…...
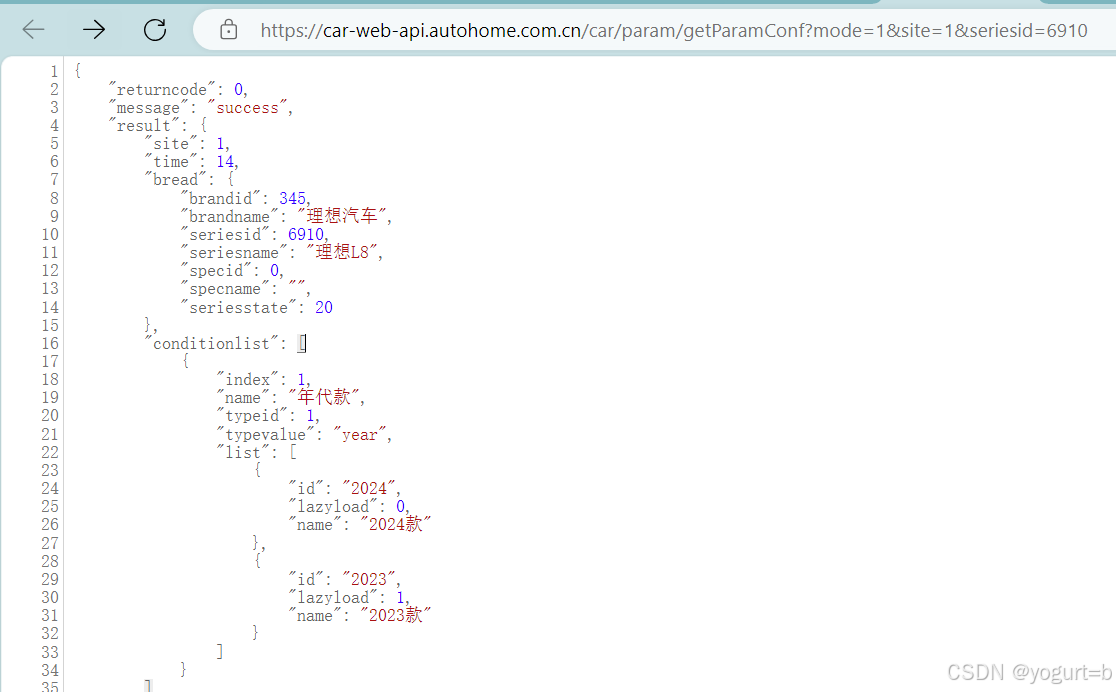
【Python爬虫】获取汽车之家车型配置附代码(2024.10)
参考大哥,感谢大哥:https://blog.csdn.net/weixin_43498642/article/details/136896338 【任务目标】 工作需要想更方便地下载汽车之家某车系配置清单;(垃圾汽车之家不给下载导出表格,配置页叉掉了车系要出来还要重新…...
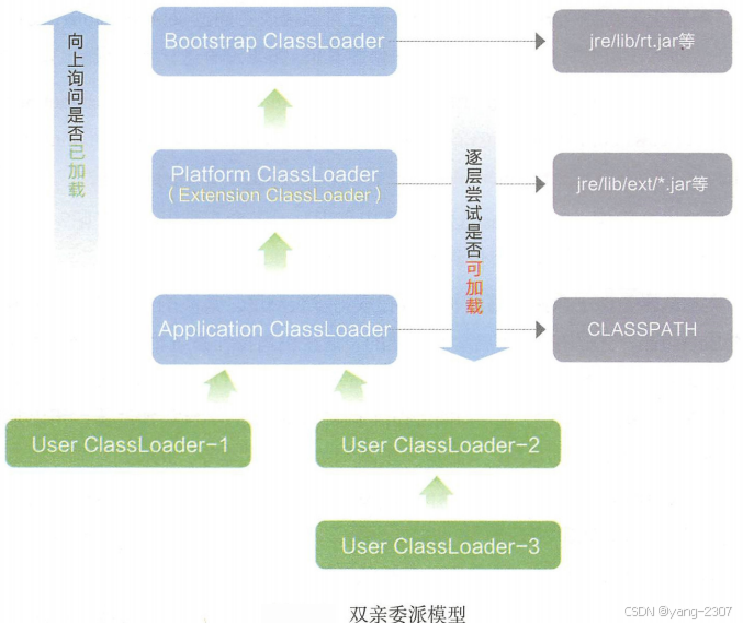
JVM 加载 class 文件的原理机制
JVM 加载 class 文件的原理机制 JVM(Java虚拟机)是一个可以执行Java字节码的虚拟机。它负责执行Java应用程序和应用程序的扩展,如Java库和框架。 文章目录 JVM 加载 class 文件的原理机制1. JVM1.1 类加载器1.2 魔数1.3 元空间 2. 类加载2.1 …...
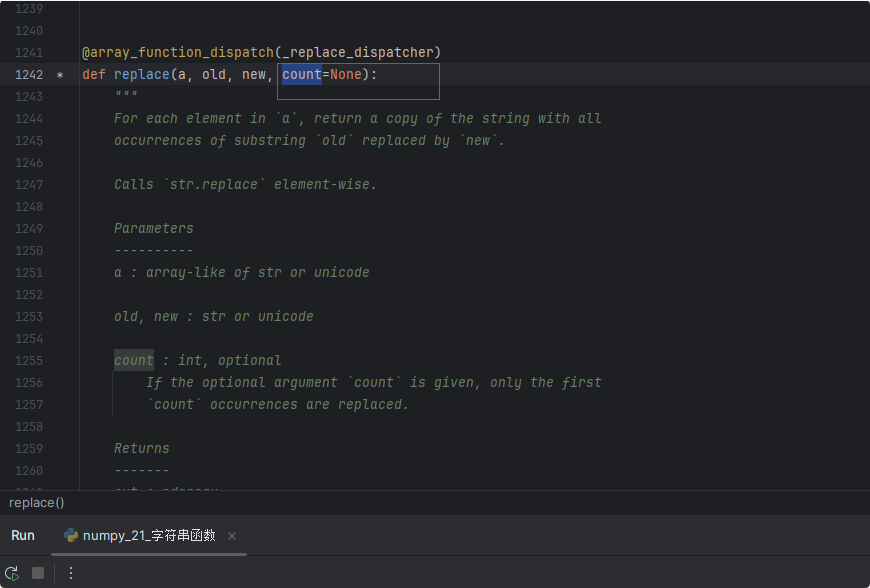
NumPy学习第九课:字符串相关函数
前言 各位有没有注意到,NumPy从第八课开始其实基本上都是讲的是NumPy的函数,而且其实就是各种函数的调用,因为NumPy是一个很强大的函数库,这对我们以后再处理项目中遇到的问题时会有很大的帮助。我们将常用的函数进行一个列举&am…...
在处理光谱特征的序列属性时表现不佳)
卷积神经网络(CNNs)在处理光谱特征的序列属性时表现不佳
卷积神经网络(CNNs)在处理光谱签名的序列属性时表现不佳,主要是由于其固有网络架构的局限性。具体原因如下: 局部感受野(Local Receptive Field): CNN 的核心操作是卷积,它利用局部感…...

【IC】MCU的Tick和晶振频率
Tick 是指 MCU 内部时钟的一个周期,通常表示为一个固定的时间间隔。每个 tick 代表一个时间单位,通常以毫秒(ms)或微秒(μs)为单位。Tick 通常由 MCU 的定时器或计时器生成,作为系统时钟的一部分…...

从0到1学习node.js(npm)
文章目录 一、NPM的生产环境与开发环境二、全局安装三、npm安装指定版本的包四、删除包 五、用npm发布一个包六、修改和删除npm包1、修改2、删除 一、NPM的生产环境与开发环境 类型命令补充生产依赖npm i -S uniq-S 等效于 --save -S是默认选项npm i -save uniq包的信息保存在…...

【STM32 Blue Pill编程实例】-OLED显示DS18B20传感器数据
OLED显示DS18B20传感器数据 文章目录 OLED显示DS18B20传感器数据1、DS18B20介绍2、硬件准备及接线3、模块配置3.1 定时器配置3.2 DS18B20传感器配置3.3 OLED的I2C接口配置4、代码实现在本文中,我们将介绍如何将 DS18B20 温度传感器与 STM32 Blue Pill 开发板连接,并使用 HAL …...

STM32 从0开始系统学习3 启动流程
目录 写在前面 速通:做了什么: 分析I:分析2011年的startup文件所作 分析II:分析2017年的startup文件所作 Helps 2011 2017 Reference 写在前面 请各位看官看本篇笔记的时候首先了解一下计算机体系架构,了解基本…...

交换机:端口安全与访问控制指南
为了实现端口安全和访问控制,交换机通常通过以下几种机制和配置来保护网络,防止未经授权的访问和恶意攻击。 01-端口安全 定义及功能 端口安全功能允许管理员限制每个交换机端口可以学习的MAC地址数量。 通过绑定特定的MAC地址到交换机的某一端口上&a…...
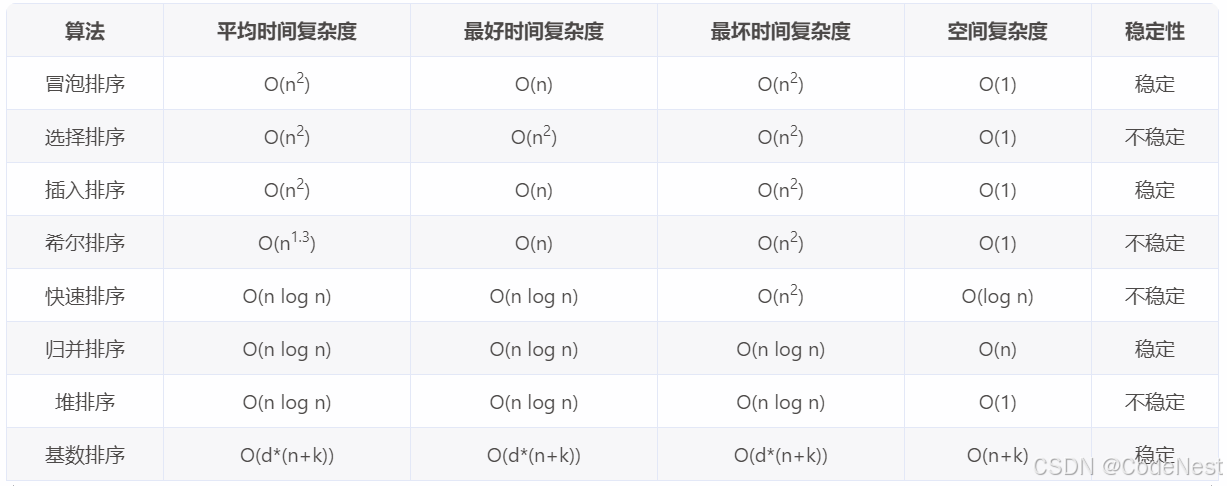
【C++ | 数据结构】八大常用排序算法详解
1. 排序的稳定性 排序是我们生活中经常会面对的问题,小朋友站队的时候会按照从矮到高的顺序排列;老师查看上课出勤情况时,会按照学生的学号点名;高考录取时,会按照成绩总分降序依次录取等等。那么对于排序它是如何定义…...

Oracle 第7章:数据完整性约束
在Oracle数据库中,数据完整性是指确保存储在数据库中的数据的正确性和一致性。为了实现这一点,Oracle提供了多种机制来维护数据完整性,包括主键(Primary Key)、外键(Foreign Key)和唯一性约束&a…...

【核心】静态/动态全覆盖路径规划相关技术研究
系列文章目录 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 TODO:写完再整理 文章目录 系列文章目录前言一、明确覆盖式路径的目标二、静态/动态全覆盖路径规划相关技术研究(1)静态全覆盖路径规划方法一:波前WaveFront 覆盖算法方法二:图形学映射算…...
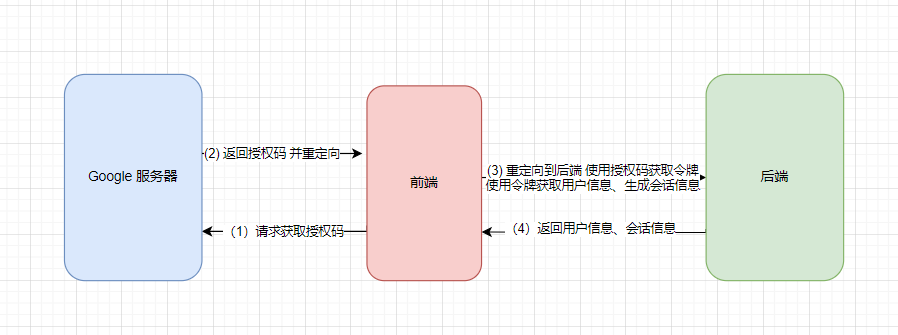
Java 实现集成 Google 邮箱第三方登录实践
文章目录 前言前期准备配置客户端 ID 和重定向 URL配置 OAuth 权限请求页面 登录流程前端演示代码后端演示代码 总结个人简介 前言 Google OAuth 2.0 是其中一种常见的第三方登录方式,广泛应用于各类网站和应用程序。通过 Google OAuth 2.0,用户可以使用…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...
