当前位置： 首页 > news >正文

EDA --软件开发之路

news 2025/9/18 16:04:43

之前一直在一家做数据处理的公司，从事c++开发，公司业务稳定，项目有忙有闲，时而看下c++，数据库，linux相关书籍，后面跳槽到了家eda公司，开始了一段eda开发之路。

eda 是 electric design automation  的缩写，是芯片设计需要用的一系列软件，其中分前端和后端，数字和模拟等，在数字电路芯片设计后端有一块称为signoff阶段，是芯片设计版图到芯片加工厂进行流片前的一个环节，用来保证芯片设计的功能、时序等满足要求。随着芯片的工艺提升，芯片中连线间的电阻电容值会影响电流，因此需要计算这里的电阻电容值，继而计算其中的延时。主流的计算电阻电容的工具有 新思的starrc，quickCap，calibre等。

电阻的计算主要是根据中学的电阻计算方式，R=\rho L/(W*T)  \rho是电阻率，L是长度，W是宽度，T是高度。

电容的计算分两种，一种是根据电容计算公式  C=Q/U，通过解微分方程进行求解，另一种是根据不同的图形位置关系，建立单位长度的电容表，利用线性插值来计算电容值。

相关文章：

EDA --软件开发之路

之前一直在一家做数据处理的公司，从事c开发，公司业务稳定，项目有忙有闲，时而看下c，数据库，linux相关书籍，后面跳槽到了家eda公司，开始了一段eda开发之路。 eda 是 electric design …...

编程日记 2024/10/31 18:16:07

51c~目标检测~合集2

我自己的原文哦~ https://blog.51cto.com/whaosoft/12377509 一、总结 这里概述了基于深度学习的目标检测器的最新发展。同时，还提供了目标检测任务的基准数据集和评估指标的简要概述，以及在识别任务中使用的一些高性能基础架构，其还涵盖了…...

编程日记 2024/10/31 18:15:03

计算机低能儿从0刷leetcode | 33.搜索旋转排列数组

题目：33. 搜索旋转排序数组 思路：看到时间复杂度要求是O(log N)很容易想到二分查找，普通的二分查找我们已经掌握，本题中的数组可以看作由两个分别升序的数组拼成，在完全升序的部分中进行二分查找是容易的，…...

编程日记 2024/10/31 18:08:55

SpringBoot+VUE2完成WebSocket聊天(数据入库)

下载依赖 <!-- websocket --><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId></dependency><!-- MybatisPlus --><dependency><groupId>com.ba…...

编程日记 2024/10/31 18:06:53

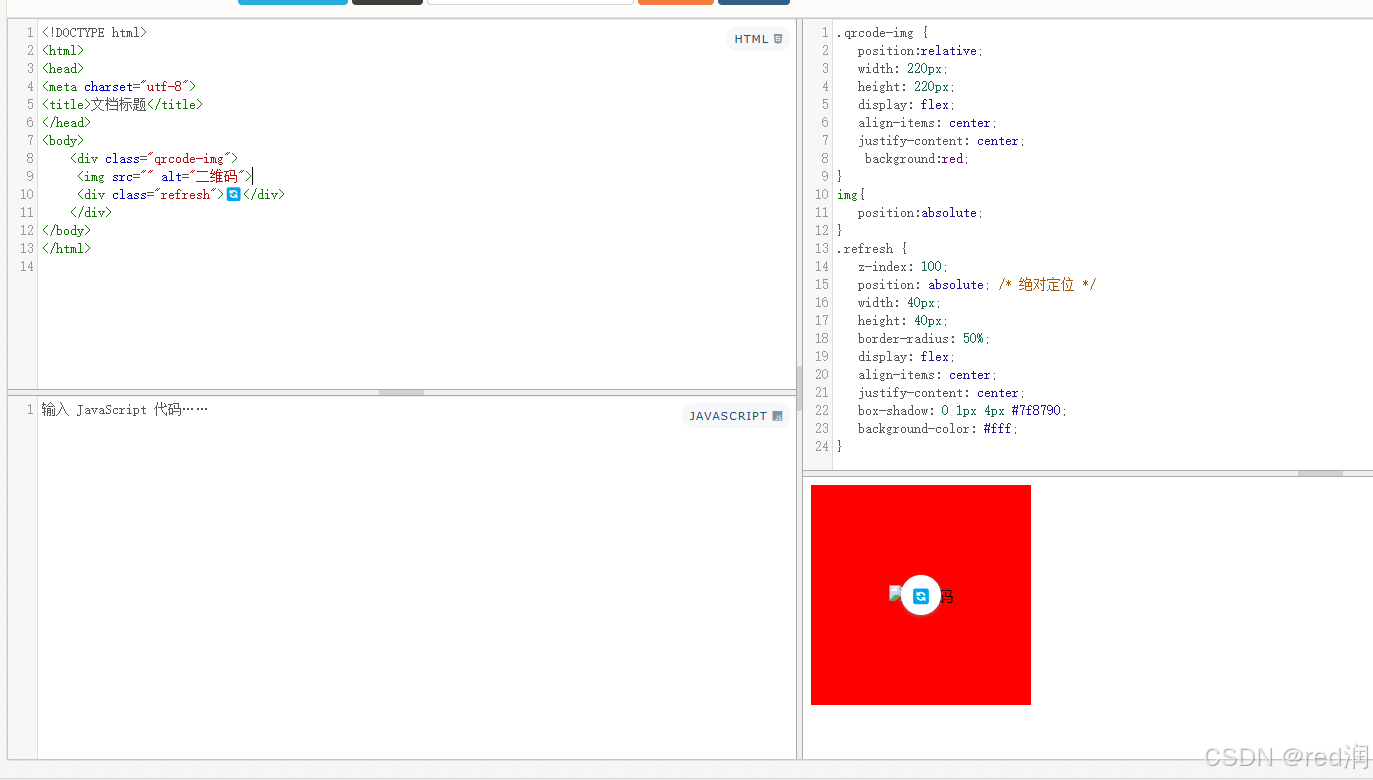
理解 CSS 中的绝对定位与 Flex 布局混用

理解 CSS 中的绝对定位与 Flex 布局混用 在现代网页设计中&#xff0c;CSS 布局技术如 flex 和绝对定位被广泛使用。然而&#xff0c;这两者结合使用时&#xff0c;可能会导致一些意想不到的布局问题。本文将探讨如何正确使用绝对定位元素&#xff0c;避免它们受到 flex 布局的…...

编程日记 2024/10/31 18:04:52

Redis 事务 问题

前言 相关系列 《Redis & 目录》《Redis & 事务 & 源码》《Redis & 事务 & 总结》《Redis & 事务 & 问题》 参考文献 《Redis事务详解》 Redis事务是什么&#xff1f; 标准的事务是指执行时具备原子性/一致性/隔离性/持久性的一系列操作。…...

编程日记 2024/10/31 18:02:49

Cpp学习手册-进阶学习

C标准库和C20新特性 C标准库概览&#xff1a; 核心库组件介绍&#xff1a; 容器&#xff1a; C 标准库提供了多种容器&#xff0c;它们各有特点&#xff0c;适用于不同的应用场景。 std::vector&#xff1a; vector&#xff1a;动态数组&#xff0c;支持快速随机访问。 #in…...

编程日记 2024/10/31 17:59:46

代码随想录-字符串-反转字符串中的单词

题目 题解 法一:纯粹为了做出本题&#xff0c;暴力解 没有技巧全是感情 class Solution {public String reverseWords(String s) {//首先去除首尾空格s s.trim();String[] strs s.split("\\s");StringBuilder sb new StringBuilder();//定义一个公共的字符反转…...

编程日记 2024/10/31 17:58:45

勒索软件通过易受攻击的 Cyber​​Panel 实例攻击网络托管服务器

一个威胁行为者&#xff08;或可能多个&#xff09;使用 PSAUX 和其他勒索软件攻击了大约 22,000 个易受攻击的 Cyber​​Panel 实例以及运行该实例的服务器上的加密文件。 PSAUX 赎金记录&#xff08;来源&#xff1a;LeakIX&#xff09; Cyber​​Panel 漏洞 Cyber​​Pane…...

编程日记 2024/10/31 17:57:44

Open WebUI + openai API / vllm API ，实战部署教程

介绍Open WebUI + Ollama 的使用: https://www.dong-blog.fun/post/1796 介绍vllm 的使用：https://www.dong-blog.fun/post/1781 介绍 Ollama 的使用： https://www.dong-blog.fun/post/1797 本篇博客玩个花的，Open WebUI 本身可以兼容openai 的api， 那来尝试一下。 仅供…...

编程日记 2024/10/31 17:56:41

InsuranceclaimsController

目录 1、 InsuranceclaimsController 1.1、 保险理赔结算 1.2、 生成预约单号 1.3、 保存索赔表 InsuranceclaimsController using QXQPS.Models; using QXQPS.Vo; using System; using System.Collections; using System.Collections.Generic; using System.Li…...

编程日记 2024/10/31 17:55:40

如何成为开源代码库Dify的contributor：解决issue并提交PR

前言 Dify 是一个开源的大语言模型&#xff08;LLM&#xff09;应用开发平台&#xff0c;它融合了后端即服务&#xff08;Backend as Service&#xff09;和LLMOps的理念&#xff0c;旨在简化和加速生成式AI应用的创建和部署。Dify提供了一个用户友好的界面和一系列强大的工具…...

编程日记 2024/10/31 17:53:38

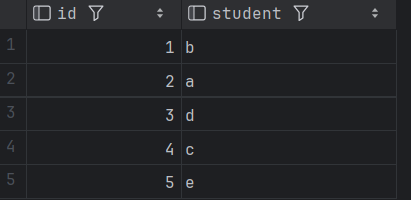
SQL进阶技巧：巧用异或运算解决经典换座位问题

目录 0 问题描述 1 数据准备 2 问题分析 2.1 什么是异或 2.2异或有什么特性？ 2.3 异或应用 2.4 本问题采用异或SQL解决方案 3 小结 0 问题描述 表 seat中有2个字段id和student id 是该表的主键（唯一值）列,student表示学生姓名。 该表的每一行都表示学生的姓名和 ID。…...

编程日记 2024/10/31 17:50:32

【MySQL】 运维篇—数据库监控：使用MySQL内置工具（如SHOW命令、INFORMATION_SCHEMA）进行监控

随着应用程序的增长&#xff0c;数据库的性能和稳定性变得至关重要。监控数据库的状态和性能可以帮助数据库管理员&#xff08;DBA&#xff09;及时发现问题&#xff0c;进行故障排查&#xff0c;并优化数据库的运行效率。通过监控工具&#xff0c;DBA可以获取实时的性能指标、…...

编程日记 2024/10/31 17:49:32

【温酒笔记】DMA

参考文档&#xff1a;野火STM32F103 1. Direct Memory Access-直接内存访问 DMA控制器独立于内核 是一个单独的外设 DMA1有7个通道DMA2有5个通道DMA有四个等级&#xff0c;非常高&#xff0c;高&#xff0c;中&#xff0c;低四个优先级如果优先等级相同&#xff0c;通道编号越…...

编程日记 2024/10/31 17:47:29

力扣判断字符是否唯一(位运算)

文章目录 给一个数n,判断它的二进制位中第x位是0还是1(从0开始计数)将一个数n的二进制位第X位修改为1(从0开始计数)将一个数n的二进制第x位修改为0(从0开始计数)提取一个数n二进制中最右侧的1去掉一个数n二进制表示中最右侧的1 今天我们通过判断字符是否唯一这个题来了解位运算…...

编程日记 2024/10/31 17:45:26

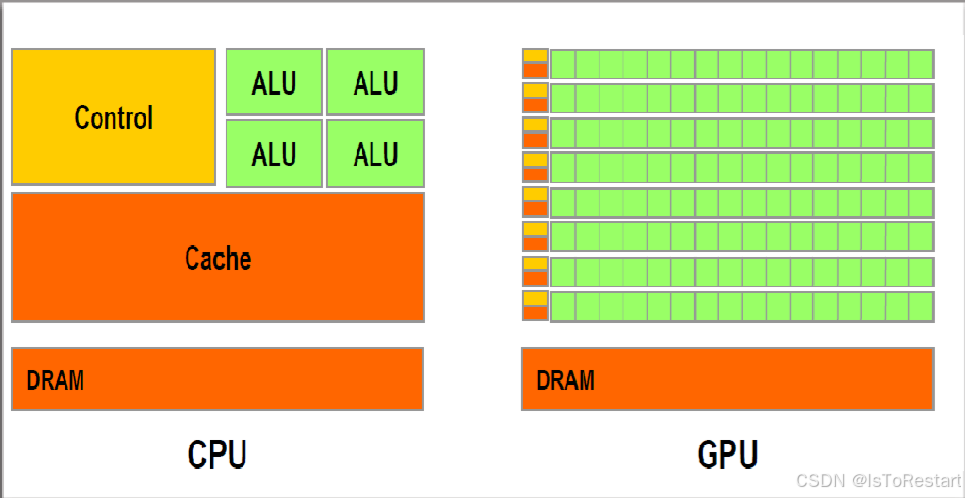
GPU和CPU区别？为什么挖矿、大模型都用GPU？

GPU(图形处理单元)和CPU(中央处理单元)是计算机中两种不同类型的处理器&#xff0c;它们在设计和功能上有很大的区别。 CPU是计算机的大脑&#xff0c;专门用于执行各种通用任务&#xff0c;如操作系统管理、数据处理、多任务处理等。它的架构设计旨在适应多种任务&#xff0c…...

编程日记 2024/10/31 17:44:25

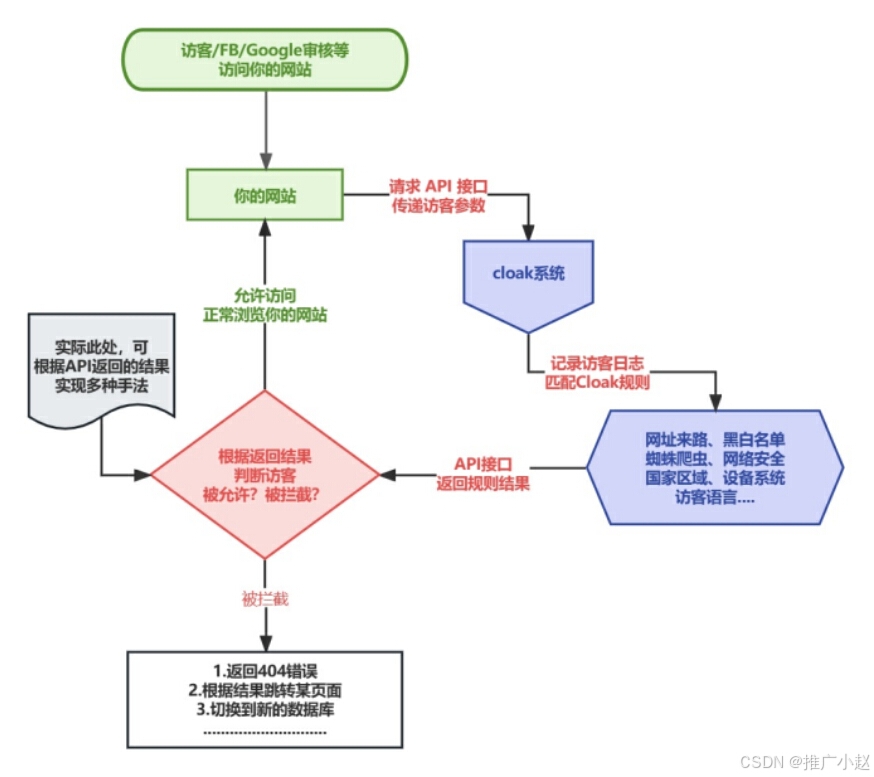
新兴斗篷cloak技术，你了解吗？

随着互联网技术的飞速发展&#xff0c;网络营销领域也经历了翻天覆地的变革。 从最早的网络横幅广告到如今主流的搜索引擎和社交媒体营销&#xff0c;广告形式变得越来越多样。 其中&#xff0c;搜索引擎广告一直以其精准投放而备受青睐&#xff0c;但近年来&#xff0c;一项名…...

编程日记 2024/10/31 17:43:23

【抽代复习笔记】34-群（二十八）：不变子群的几道例题

例1&#xff1a;证明&#xff0c;交换群的任何子群都是不变子群。 证&#xff1a;设(G,o)是交换群&#xff0c;H≤G&#xff0c; 对任意的a∈G&#xff0c;显然都有aH {a o h|h∈H} {h o a|h∈H} Ha。 所以H⊿G。 【注&#xff1a;规范的不变子群符号是一个顶角指向左边…...

编程日记 2024/10/31 17:41:19

Chrome和Firefox如何保护用户的浏览数据

在当今数字化时代&#xff0c;保护用户的浏览数据变得尤为重要。浏览器作为我们日常上网的主要工具&#xff0c;其安全性直接关系到个人信息的保密性。本文将详细介绍Chrome和Firefox这两款主流浏览器如何通过一系列功能来保护用户的浏览数据。&#xff08;本文由https://chrom…...

编程日记 2024/10/31 17:40:17

Linux 文件类型，目录与路径，文件与目录管理

文件类型 后面的字符表示文件类型标志 普通文件&#xff1a;-&#xff08;纯文本文件&#xff0c;二进制文件&#xff0c;数据格式文件&#xff09; 如文本文件、图片、程序文件等。 目录文件&#xff1a;d&#xff08;directory&#xff09; 用来存放其他文件或子目录。 设备…...

编程新知 2025/9/15 5:22:58

golang循环变量捕获问题​​

在 Go 语言中&#xff0c;当在循环中启动协程&#xff08;goroutine&#xff09;时&#xff0c;如果在协程闭包中直接引用循环变量&#xff0c;可能会遇到一个常见的陷阱 - ​​循环变量捕获问题​​。让我详细解释一下&#xff1a; 问题背景 看这个代码片段&#xff1a; fo…...

编程新知 2025/7/5 11:03:11

Unity3D中Gfx.WaitForPresent优化方案

前言 在Unity中&#xff0c;Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染&#xff08;即CPU被阻塞&#xff09;&#xff0c;这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案&#xff1a; 对惹&#xff0c;这里有一个游戏开发交流小组&…...

编程新知 2025/9/18 9:42:12

Qt Widget类解析与代码注释

#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码&#xff0c;写上注释 当然可以&#xff01;这段代码是 Qt …...

编程新知 2025/6/15 21:47:30

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控，故障处理工具

第2章 虚拟机性能监控&#xff0c;故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令&#xff1a;jps [options] [hostid] 功能&#xff1a;本地虚拟机进程显示进程ID&#xff08;与ps相同&#xff09;&#xff0c;可同时显示主类&#x…...

编程新知 2025/9/7 19:10:42

有限自动机到正规文法转换器v1.0

1 项目简介 这是一个功能强大的有限自动机&#xff08;Finite Automaton, FA&#xff09;到正规文法&#xff08;Regular Grammar&#xff09;转换器&#xff0c;它配备了一个直观且完整的图形用户界面&#xff0c;使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

编程新知 2025/9/12 22:46:16

Java + Spring Boot + Mybatis 实现批量插入

在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法&#xff1a;使用 MyBatis 的 <foreach> 标签和批处理模式&#xff08;ExecutorType.BATCH&#xff09;。 方法一&#xff1a;使用 XML 的 <foreach> 标签&#xff…...

编程新知 2025/6/11 2:44:05

基于Java+MySQL实现（GUI）客户管理系统

客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息&#xff0c;对客户进行统一管理&#xff0c;可以把所有客户信息录入系统&#xff0c;进行维护和统计功能。可通过文件的方式保存相关录入数据&#xff0c;对…...

编程新知 2025/9/7 3:22:38

处理vxe-table 表尾数据是单独一个接口，表格tableData数据更新后，需要点击两下，表尾才是正确的

修改bug思路&#xff1a; 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑&#xff1a;async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

编程新知 2025/9/11 8:54:35

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要&#xff1a; 近期&#xff0c;在使用较新版本的OpenSSH客户端连接老旧SSH服务器时&#xff0c;会遇到 "no matching key exchange method found"​, "n…...

编程新知 2025/6/15 18:10:15