【小白学机器学习28】 统计学脉络+ 总体+ 随机抽样方法
目录
参考书,学习书
0 统计学知识大致脉络
1 个体---抽样---整体
1.1 关于个体---抽样---整体,这个三段式关系
1.2 要明白,自然界的整体/母体是不可能被全部认识的
1.2.1 不要较真,如果是人为定义的一个整体,是可以被认识的
1.2.2 如果是自然界/社会上的整体/母体,一般都不能被全部认识
1.2.3 从哲学上说,整体/母体是彼岸的东西,是理念,是绝对精神,是大脑中先验的范式。
1.2.4 反过来说,整体/母体 完全不可知吗?是部分可知的
2 数据的来源
2.1 数据的来源
2.2 数据的层级
2.3 样本是什么sample?
3 如何获得样本数据?
3.1 随机抽样不是随意调查
3.2 等距抽样
3.3 分层抽样
3.4 群抽样
3.5 混合多阶段抽样
参考书,学习书
- 日本,图解统计学,今野纪雄
- 日本,新手小白学统计,本丸谅
- 《从零开始学统计》 归璐
- 《戏说统计》李连江
0 统计学知识大致脉络
- 需要对统计学有个大致脉络
- 不至于完全陷入到细节里去,时刻清楚自己在地图的哪儿

1 个体---抽样---整体
1.1 关于个体---抽样---整体,这个三段式关系
- 个体---抽样---整体/母体
- case---sample---polulation
- 普通----特殊----整体
- 这个类黑格尔的三段式逻辑的内涵:
- 我们想从个别例子认识到整体,总结到一般规律,中间必须要借用1个逻辑步骤:抽样样本。
- 也就是用1个命题+另外1个命题→得到结论的一种推理方式
黑格尔式三段论逻辑:
人都要吃饭
男人是人
所以男人要吃饭
科学网—“三段论(Syllogism)”简介 - 柳渝的博文
在传统逻辑中,“三段论(Syllogism)”指从两个命题(“大前提”和“小前提”)推导出“结论”的一种推理形式,是数学证明、科学研究及日常沟通交流中常用的一种推理。
在希腊语中,syllogism由syn(与)和logos(语言)组成,本意指“(一个命题)与(另一个命题)相连”,引申义指“推理”。亚里士多德在“工具论(Organon)”中第一次将三段论系统化。
例子:
- 所有人都是必死的。(大前提)
- 苏格拉底是人。(小前提)
- 苏格拉底是必死的。(结论)
1.2 要明白,自然界的整体/母体是不可能被全部认识的
1.2.1 不要较真,如果是人为定义的一个整体,是可以被认识的
- 我们自己当然可以自己定义一个我们全知的“整体”
- 在这个角度,我们就是上帝
- 但是这个知识“题目”“模型”“思想试验” ,我们可以在我们定义的世界里有上帝视角,这不奇怪。
- 就和做题 != 解决社会上的真实问题一样,这些整体,一般并不是我们要面对的生活中的自然的/社会上的真正整体。
类比的例子
- 定距数据里,比如摄氏度,身高,我们也可以进行* /,因为我们预设了一个0点,温度0,身高0。那为什么说定距数据里,进行* /运算没有意义?
- 是因为别人可以设置 -10度,-20作为温度和身高的起点,这样计算乘除的结果就完全不同了。所以是没有意义的。
- 只有用绝对0度当0度的华氏温度才有 */的意义。
1.2.2 如果是自然界/社会上的整体/母体,一般都不能被全部认识
大整体/母体的特点
- 理论都是无穷的,无法穷尽数量的,所以我们不可能认识真正的全部集合里的所有元素!
- 获得巨大量的数据,成本是很高的。
- 等等原因
1.2.3 从哲学上说,整体/母体是彼岸的东西,是理念,是绝对精神,是大脑中先验的范式。
- 从柏拉图等观点来看
- 因为真正的母体/总体我们无法认识,其实这些是概念,不存在于现实世界,只存在于彼岸世界,是所谓的“形而上”
- 而我们所有的现实生活的一个个集合,都是对这个概念的一个拙劣的投射/模仿(反正就是这个意思吧,我水平就只能描述道这)
1.2.4 反过来说,整体/母体 完全不可知吗?是部分可知的
- 哲学里对立的观点本来就很多
- 有“形而上”的观点,也有 纯经验的观点,比如经验主义,现象学等等
- 这个不说了,作为普通人的我把握不住。
我认为
- 真正的整体也许确实永远不可能被全部认识
- 整体是部分可知的
- 或者说,整体的一些现实投射是可知的。
- 我们的日常经验就是对整体的一些认识,这些就是我们认识的材料。
2 数据的来源
2.1 数据的来源
- 调查,问卷等
- 统计
2.2 数据的层级
- 个体:case ,特殊化
- 整体/母体:不可知
- 进行普查:几乎不可能
- 进行全面调查,很难,成本很高
- 所以我们要通过样本取认识整体,样本是什么?
2.3 样本是什么sample?
- 样本是整体的一部分
- 样本不是整体的随便一部分
- 样本是整体的微缩/结构相同/类似/缩小版
但是问题来了
- 我们连整体都不能全知,我们怎么知道样本是否和总体是结构类似的?
- 我们不能保证(因为我们确实验证不了)
- 我们最多只能从过程中保证
3 如何获得样本数据?
- 我们最多只能从过程中保证,样本类似整体,怎么做?
- 只能从过程上尽量保证随机:每个个体均等机会被抽中。
- 取样的原则1:公平
- 取样的原则2:成本可控时,抽样数量要尽可能多一点
保证总体中每个case有相同的概率被抽取到!
这需要考虑到很多
这些case 在各个属性维度上,都要是相同,平等的概率
比如人口调查,需要让人口从年龄,学历,地域,,,,各个维度都平等的抽到
- 具体的手段:随机抽样/等距抽样,等等
3.1 随机抽样不是随意调查
- 抽样调查
- 正确:比如给每个个体编号,然后取随机抽取这些编号
- 错误:比如给每个个体编号,挑选编号前100个
3.2 等距抽样
- 比如给每个个体编号,然后按一定距离比如相距10个抽1个
- 1,11,21,等等
3.3 分层抽样
- 如果我们知道数据是分层的
- 并且,我们可以用一些辅助数据可以区分这些分层
- 那么我们可以在不同的分层中分别抽取数据
数据分层:(有点像聚类分析,不同的类别)
- 分层间,数据差异大
- 分层内,数据差异比较小
3.4 群抽样
- 从直接抽个体,变成直接抽群
- 群抽样的特点例子,比如学校学生等天然就是分群的
群抽样和分层抽样差异
- 群抽样,每个群体之间差异小,群里尽量是差异很大,每个群内部都类整体分布
- 分层抽样相反,层之间差异大,层内差异小。
3.5 混合多阶段抽样
比较复杂,我没仔细看~~
反正就是利用上面各种抽样的优点
相关文章:

【小白学机器学习28】 统计学脉络+ 总体+ 随机抽样方法
目录 参考书,学习书 0 统计学知识大致脉络 1 个体---抽样---整体 1.1 关于个体---抽样---整体,这个三段式关系 1.2 要明白,自然界的整体/母体是不可能被全部认识的 1.2.1 不要较真,如果是人为定义的一个整体,是可…...

安全研究 | 不同编程语言中 IP 地址分类的不一致性
作为一名安全研究人员,我分析了不同编程语言中 IP 地址分类 的行为。最近,我注意到一些有趣的不一致性,特别是在循环地址和私有 IP 地址的处理上。在这篇文章中,我将分享我对此问题的观察和见解。 设置 我检查了多种编程语言&am…...

小小的表盘还能玩出这么多花样?华为手表这次细节真的拉满
没想到小小的表盘还能玩出这么多花样?华为这次细节真的拉满!还有没有你不知道的神奇玩法? 情绪萌宠,心情状态抬腕可见 好心情就像生活馈赠的糖果,好的心情让我们遇到困难也不惧打击!HUAWEI WATCH GT 5情绪…...

trueNas 24.10 docker配置文件daemon.json无法修改(重启被覆盖)解决方案
前言 最近听说truenas的24.10版本开放docker容器解决方案放弃了原来难用的k3s,感觉非常巴适,就研究了一下,首先遇到无法迁移老系统应用问题比较好解决,使用sudo登录ssh临时修改daemon.json重启docker后进行docker start 容器即可…...

数字孪生,概念、应用与未来展望
随着科技的飞速发展,数字化已经成为各行各业的发展趋势,在这个过程中,数字孪生作为一种新兴的技术,逐渐引起了人们的关注,本文将对数字孪生的概念、应用以及未来展望进行详细介绍。 数字孪生的概念: 数字孪…...

Chromium HTML Input 类型Text 对应c++
一、文本域(Text Fields) 文本域通过 <input type"text"> 标签来设定,当用户要在表单中键入字母、数字等内容时,就会用到文本域。 <!DOCTYPE html> <html> <head> <meta charset"ut…...

SpringMvc参数传递
首先对于post请求汉字乱码需要进行过滤器配置 普通参数传递 直接传递 客户端传递的属性名与我的bean中的函数参数名相同 映射传递RequestParam("XXX") 在我们方法参数中定义一个与客户端属性名一致 并绑定参数 POJO实体类传递 嵌套POJO传递 数组likes参数传递…...

西安国际数字影像产业园:数字化建设赋能产业升级与拓展
西安国际数字影像产业园的数字化建设,在当前经济与科技迅猛发展的大背景下,已然成为提升园区管理效率、服务水平以及运营效果的关键趋势。随着信息技术日新月异的进步,数字化更是成为这座产业园转型升级的核心关键词。如今,西安国…...

linux线程池
线程池: * 一种线程使用模式。线程过多会带来调度开销,进而影响缓存局部性和整体性能。而线程池维护着多个线程,等待着 监督管理者分配可并发执行的任务。这避免了在处理短时间任务时创建与销毁线程的代价。线程池不仅能够保证内核的充分利 用࿰…...

PyTorch图像分类实战——基于ResNet18的RAF-DB情感识别(附完整代码和结果图)
PyTorch图像分类实战——基于ResNet18的RAF-DB情感识别(附完整代码和结果图) 关于作者 作者:小白熊 作者简介:精通python、matlab、c#语言,擅长机器学习,深度学习,机器视觉,目标检测…...

【OccNeRF: Advancing 3D Occupancy Prediction in LiDAR-Free Environments】阅读笔记
【OccNeRF: Advancing 3D Occupancy Prediction in LiDAR-Free Environments】阅读笔记 1. 论文概述Abstract1. Introduction2. Related work2.1 3D Occupancy Prediction2.2 Neural Radiance Fields2.3 Self-supervised Depth Estimation 3. Method3.1 Parameterized Occupanc…...

DDRPHY数字IC后端设计实现系列专题之后端设计导入,IO Ring设计
本章详细分析和论述了 LPDDR3 物理层接口模块的布图和布局规划的设计和实 现过程,包括设计环境的建立,布图规划包括模块尺寸的确定,IO 单元、宏单元以及 特殊单元的摆放。由于布图规划中的电源规划环节较为重要, 影响芯片的布线资…...
EDA --软件开发之路
之前一直在一家做数据处理的公司,从事c开发,公司业务稳定,项目有忙有闲,时而看下c,数据库,linux相关书籍,后面跳槽到了家eda公司,开始了一段eda开发之路。 eda 是 electric design …...
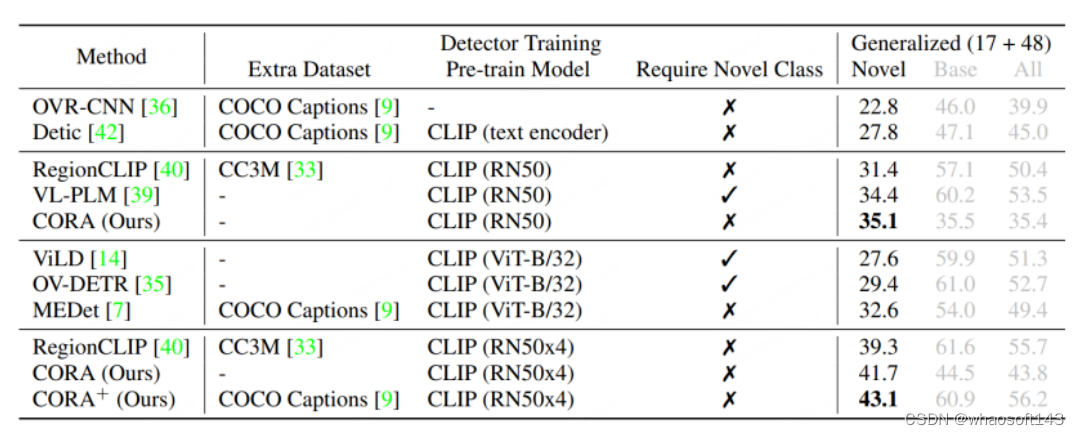
51c~目标检测~合集2
我自己的原文哦~ https://blog.51cto.com/whaosoft/12377509 一、总结 这里概述了基于深度学习的目标检测器的最新发展。同时,还提供了目标检测任务的基准数据集和评估指标的简要概述,以及在识别任务中使用的一些高性能基础架构,其还涵盖了…...

计算机低能儿从0刷leetcode | 33.搜索旋转排列数组
题目:33. 搜索旋转排序数组 思路:看到时间复杂度要求是O(log N)很容易想到二分查找,普通的二分查找我们已经掌握,本题中的数组可以看作由两个分别升序的数组拼成,在完全升序的部分中进行二分查找是容易的,…...
SpringBoot+VUE2完成WebSocket聊天(数据入库)
下载依赖 <!-- websocket --><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId></dependency><!-- MybatisPlus --><dependency><groupId>com.ba…...
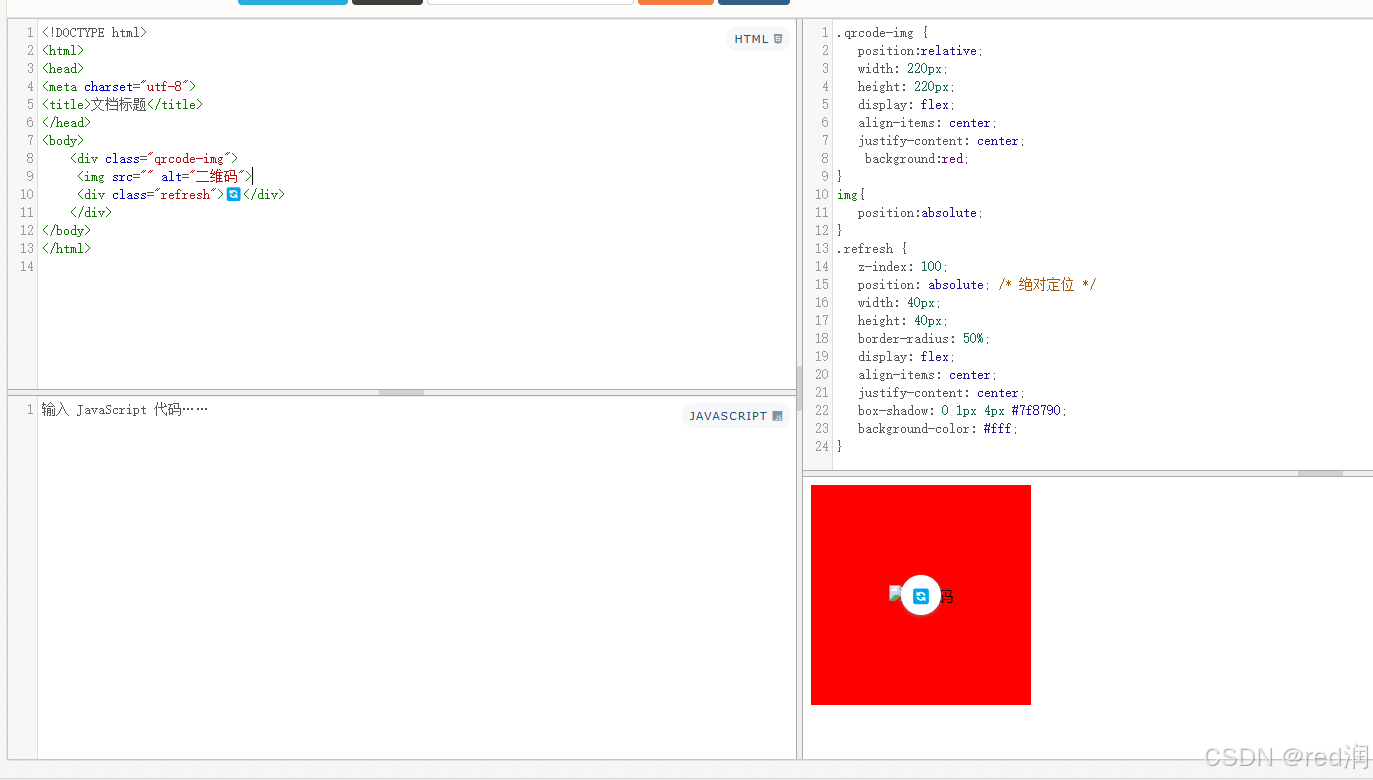
理解 CSS 中的绝对定位与 Flex 布局混用
理解 CSS 中的绝对定位与 Flex 布局混用 在现代网页设计中,CSS 布局技术如 flex 和绝对定位被广泛使用。然而,这两者结合使用时,可能会导致一些意想不到的布局问题。本文将探讨如何正确使用绝对定位元素,避免它们受到 flex 布局的…...

Redis 事务 问题
前言 相关系列 《Redis & 目录》《Redis & 事务 & 源码》《Redis & 事务 & 总结》《Redis & 事务 & 问题》 参考文献 《Redis事务详解》 Redis事务是什么? 标准的事务是指执行时具备原子性/一致性/隔离性/持久性的一系列操作。…...

Cpp学习手册-进阶学习
C标准库和C20新特性 C标准库概览: 核心库组件介绍: 容器: C 标准库提供了多种容器,它们各有特点,适用于不同的应用场景。 std::vector: vector:动态数组,支持快速随机访问。 #in…...

代码随想录-字符串-反转字符串中的单词
题目 题解 法一:纯粹为了做出本题,暴力解 没有技巧全是感情 class Solution {public String reverseWords(String s) {//首先去除首尾空格s s.trim();String[] strs s.split("\\s");StringBuilder sb new StringBuilder();//定义一个公共的字符反转…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...
