高阶数据结构--图(graph)
图(graph)
- 1.并查集
- 1. 并查集原理
- 2. 并查集实现
- 3. 并查集应用
- 2.图的基本概念
- 3. 图的存储结构
- 3.1 邻接矩阵
- 3.2 邻接矩阵的代码实现
- 3.3 邻接表
- 3.4 邻接表的代码实现
- 4. 图的遍历
- 4.1 图的广度优先遍历
- 4.2 广度优先遍历的代码
1.并查集
1. 并查集原理
在一些应用问题中,需要将n个不同的元素划分成一些不相交的集合。开始时,每个元素自成一个单元素集合,然后按一定的规律将归于同一组元素的集合合并。在此过程中要反复用到查询某一个元素归属于那个集合的运算。适合于描述这类问题的抽象数据类型称为并查集(union-find
set)。
比如:某公司今年校招全国总共招生10人,西安招4人,成都招3人,武汉招3人,10个人来自不
同的学校,起先互不相识,每个学生都是一个独立的小团体,现给这些学生进行编号:{0, 1, 2, 3,4, 5, 6, 7, 8, 9}; 给以下数组用来存储该小集体,数组中的数字代表:该小集体中具有成员的个
数。(负号下文解释)

毕业后,学生们要去公司上班,每个地方的学生自发组织成小分队一起上路,于是:
西安学生小分队s1={0,6,7,8},成都学生小分队s2={1,4,9},武汉学生小分队s3={2,3,5}就相互认识了,10个人形成了三个小团体。假设右三个群主0,1,2担任队长,负责大家的出行。

一趟火车之旅后,每个小分队成员就互相熟悉,称为了一个朋友圈。

从上图可以看出:编号6,7,8同学属于0号小分队,该小分队中有4人(包含队长0);编号为4和9的同学属于1号小分队,该小分队有3人(包含队长1),编号为3和5的同学属于2号小分队,该小分队有3个人(包含队长1)。
仔细观察数组中内融化,可以得出以下结论:
- 数组的下标对应集合中元素的编号
- 数组中如果为负数,负号代表根,数字代表该集合中元素个数
- 数组中如果为非负数,代表该元素双亲在数组中的下标
在公司工作一段时间后,西安小分队中8号同学与成都小分队1号同学奇迹般的走到了一起,两个
小圈子的学生相互介绍,最后成为了一个小圈子:

现在0集合有7个人,2集合有3个人,总共两个朋友圈。
通过以上例子可知,并查集一般可以解决一下问题:
- 查找元素属于哪个集合
沿着数组表示树形关系以上一直找到根(即:树中中元素为负数的位置) - 查看两个元素是否属于同一个集合
沿着数组表示的树形关系往上一直找到树的根,如果根相同表明在同一个集合,否则不在 - 将两个集合归并成一个集合
-将两个集合中的元素合并
-将一个集合名称改成另一个集合的名称 - 集合的个数
遍历数组,数组中元素为负数的个数即为集合的个数。
2. 并查集实现
template<class T>
class UnionFindSet
{
public:UnionFindSet(size_t n):_ufs(n,-1){}int Find(int x)//查找根{int root = x;while (_ufs[root] >= 0){root = _ufs[root];}return root;}void Union(int x1, int x2){int x = Find(x1);int y = Find(x2);if (x == y)return;//本来就在一个团体_ufs[x] += _ufs[y];_ufs[y] = x;}bool Inset(int x1, int x2){return Find(x1) == Find(x2);}size_t SetSize(){size_t size = 0;for (size_t i = 0; i < _ufs.size(); i++){if (_ufs[i] < 0)size++;}return size;}private:vector<T> _ufs;
};
此外为了学习图这个非常难得数据结构我这里补充一下通过编号找名字,通过名字找编号如何实现:
//template<class T>
//class UnionFindSet
//{
//public:
//
// UnionFindSet(const T* a, const size_t n)
// {
// for (size_t i = 0; i < n; i++)
// {
// _a.push_back(a[i]);
// _indexMap[a[i]] = i;
// }
// }
//
//private:
// vector<T> _a;//编号找名字
// map<T, int> _indexMap;//名字找编号
//};
实现后的效果如图:

将以上内容理解清楚我们才能进入更好地进入图的学习。
3. 并查集应用
https://leetcode.cn/problems/bLyHh0/
https://leetcode-cn.com/problems/satisfiability-of-equality-equations/comments/
以上两个题就是并查集能解决的问题,由于我们主要的目标是学习图,所以需要答案可以私信我
2.图的基本概念
图是由顶点集合及顶点间的关系组成的一种数据结构:G = (V, E),其中:
顶点集合V = {x|x属于某个数据对象集}是有穷非空集合;
E = {(x,y)|x,y属于V}或者E = {<x, y>|x,y属于V && Path(x, y)}是顶点间关系的有穷集合,也叫
做边的集合。
(x, y)表示x到y的一条双向通路,即(x, y)是无方向的;Path(x, y)表示从x到y的一条单向通路,即
Path(x, y)是有方向的。
顶点和边:图中结点称为顶点,第i个顶点记作vi。两个顶点vi和vj相关联称作顶点vi和顶点vj之间
有一条边,图中的第k条边记作ek,ek = (vi,vj)或<vi,vj>。
有向图和无向图:在有向图中,顶点对<x, y>是有序的,顶点对<x,y>称为顶点x到顶点y的一条
边(弧),<x, y>和<y, x>是两条不同的边,比如下图G3和G4为有向图。在无向图中,顶点对(x, y)
是无序的,顶点对(x,y)称为顶点x和顶点y相关联的一条边,这条边没有特定方向,(x, y)和(y,x)
是同一条边,比如下图G1和G2为无向图。注意:无向边(x, y)等于有向边<x, y>和<y, x>。

完全图:在有n个顶点的无向图中,若有n * (n-1)/2条边,即任意两个顶点之间有且仅有一条边,
则称此图为无向完全图,比如上图G1;在n个顶点的有向图中,若有n * (n-1)条边,即任意两个
顶点之间有且仅有方向相反的边,则称此图为有向完全图,比如上图G4。
邻接顶点:在无向图中G中,若(u, v)是E(G)中的一条边,则称u和v互为邻接顶点,并称边(u,v)依附于顶点u和v;在有向图G中,若<u, v>是E(G)中的一条边,则称顶点u邻接到v,顶点v邻接自顶点u,并称边<u, v>与顶点u和顶点v相关联。
顶点的度:顶点v的度是指与它相关联的边的条数,记作deg(v)。在有向图中,顶点的度等于该顶点的入度与出度之和,其中顶点v的入度是以v为终点的有向边的条数,记作indev(v);顶点v的出度是以v为起始点的有向边的条数,记作outdev(v)。因此:dev(v) = indev(v) + outdev(v)。注
意:对于无向图,顶点的度等于该顶点的入度和出度,即dev(v) = indev(v) = outdev(v)。
路径:在图G = (V, E)中,若从顶点vi出发有一组边使其可到达顶点vj,则称顶点vi到顶点vj的顶
点序列为从顶点vi到顶点vj的路径。
路径长度:对于不带权的图,一条路径的路径长度是指该路径上的边的条数;对于带权的图,一
条路径的路径长度是指该路径上各个边权值的总和。

简单路径与回路:若路径上各顶点v1,v2,v3,…,vm均不重复,则称这样的路径为简单路
径。若路径上第一个顶点v1和最后一个顶点vm重合,则称这样的路径为回路或环。

子图:设图G = {V, E}和图G1 = {V1,E1},若V1属于V且E1属于E,则称G1是G的子图。

连通图:在无向图中,若从顶点v1到顶点v2有路径,则称顶点v1与顶点v2是连通的。如果图中任意一对顶点都是连通的,则称此图为连通图。
强连通图:在有向图中,若在每一对顶点vi和vj之间都存在一条从vi到vj的路径,也存在一条从vj
到vi的路径,则称此图是强连通图。
生成树:一个连通图的最小连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点
和n-1条边。
3. 图的存储结构
因为图中既有节点,又有边(节点与节点之间的关系),因此,在图的存储中,只需要保存:节点和边关系即可。节点保存比较简单,只需要一段连续空间即可,那边关系该怎么保存呢?
3.1 邻接矩阵
因为节点与节点之间的关系就是连通与否,即为0或者1,因此邻接矩阵(二维数组)即是:先用一
个数组将定点保存,然后采用矩阵来表示节点与节点之间的关系。

注意:
- 无向图的邻接矩阵是对称的,第i行(列)元素之和,就是顶点i的度。有向图的邻接矩阵则不一
定是对称的,第i行(列)元素之后就是顶点i 的出(入)度。 - 如果边带有权值,并且两个节点之间是连通的,上图中的边的关系就用权值代替,如果两个
顶点不通,则使用无穷大代替。

- 用邻接矩阵存储图的有点是能够快速知道两个顶点是否连通,缺陷是如果顶点比较多,边比
较少时,矩阵中存储了大量的0成为系数矩阵,比较浪费空间,并且要求两个节点之间的路
径不是很好求。
3.2 邻接矩阵的代码实现
namespace matrix
{template<class V, class W, W MAX = INT_MAX, bool Direction = false>class Graph{public:Graph(const V* a, size_t n){_vertexs.reserve(n);for (size_t i = 0; i < n; i++){_vertexs.push_back(a[i]);//存放顶点_IndexMap[a[i]] = i;//存放顶点,并建立顶点与下标的映射关系}_matrix.resize(n);for (int i = 0; i < _matrix.size(); i++){_matrix[i].resize(n, MAX);}}size_t GetIndexMap(const V& v){auto it = _IndexMap.find(v);if (it != _IndexMap.end())return it->second;else{return -1;}}void AddEdge(const V& src, const V& dst, const W& w){size_t srci = GetIndexMap(src);size_t dsti = GetIndexMap(dst);_matrix[srci][dsti] = w;if (Direction == false){_matrix[dsti][srci] = w;}}void Print(){cout <<" ";for (size_t i = 0; i < _vertexs.size(); i++){printf("%4d", i);}cout << endl;for (size_t i = 0; i < _matrix.size(); i++){cout << i << ' ';for (size_t j = 0; j < _matrix[i].size(); j++){if (_matrix[i][j] == MAX)printf("%4c", '&');elseprintf("%4d", _matrix[i][j]);}cout << endl;}}private:vector<V> _vertexs;//顶点集map<V,int> _IndexMap;//下标和顶点映射关系vector<vector<W>> _matrix;//邻接矩阵};void test1(){Graph<char, int, INT_MAX, false> g("0123", 4);g.AddEdge('0', '0', 1);g.AddEdge('1', '1', 2);g.AddEdge('2', '2', 3);g.AddEdge('3', '3', 4);g.Print();}}
3.3 邻接表
邻接表:使用数组表示顶点的集合,使用链表表示边的关系。
-
无向图邻接表存储

注意:无向图中同一条边在邻接表中出现了两次。如果想知道顶点vi的度,只需要知道顶点
vi边链表集合中结点的数目即可。 -
有向图邻接表存储

注意:有向图中每条边在邻接表中只出现一次,与顶点vi对应的邻接表所含结点的个数,就
是该顶点的出度,也称出度表,要得到vi顶点的入度,必须检测其他所有顶点对应的边链
表,看有多少边顶点的dst取值是i。
3.4 邻接表的代码实现
namespace Link_table
{template<class W>struct Edge{W _w;//int _srci;size_t _dsti;//指向的点Edge<W>* _next;Edge(size_t dsti,const W& w):_dsti(dsti),_w(w),_next(nullptr){}};template<class V, class W, bool Direction = false>class Graph{typedef Edge<W> Edge;public:Graph(const V* a, size_t n){_vertexs.reserve(n);for (size_t i = 0; i < n; i++){_vertexs.push_back(a[i]);//存放顶点_IndexMap[a[i]] = i;//存放顶点,并建立顶点与下标的映射关系}_linktable.resize(n,nullptr);}size_t GetIndexMap(const V& v){auto it = _IndexMap.find(v);if (it != _IndexMap.end()){return it->second;}else{return -1;}}void AddEdge(const V& src, const V& dst, const W& w){size_t srci = GetIndexMap(src);size_t dsti = GetIndexMap(dst);Edge* eg = new Edge(dsti, w);eg->_next = _linktable[srci];_linktable[srci] = eg;if (Direction == false){Edge* eg = new Edge(srci, w);eg->_next = _linktable[dsti];_linktable[dsti] = eg;}}void Print(){for (size_t i = 0; i < _linktable.size(); i++){cout << _vertexs[i] << " ";Edge* cur = _linktable[i];while (cur){cout << _vertexs[cur->_dsti] << ":" << cur->_w << "->";cur = cur->_next;}cout << "nullptr";cout << endl;}}private:vector<V> _vertexs;//顶点集map<V, int> _IndexMap;//下标和顶点映射关系vector<Edge*> _linktable;//};void test1(){string a[] = { "张三", "李四", "王五", "赵六" };Graph<string, int, true> g1(a, 4);g1.AddEdge("张三", "李四", 100);g1.AddEdge("张三", "王五", 200);g1.AddEdge("王五", "赵六", 30);g1.Print();}}
4. 图的遍历
给定一个图G和其中任意一个顶点v0,从v0出发,沿着图中各边访问图中的所有顶点,且每个顶
点仅被遍历一次。"遍历"即对结点进行某种操作的意思。
请思考树以前是怎么遍历的,此处可以直接用来遍历图吗?为什么?
4.1 图的广度优先遍历


4.2 广度优先遍历的代码
namespace matrix
{template<class V, class W, W MAX = INT_MAX, bool Direction = false>class Graph{public:Graph(const V* a, size_t n){_vertexs.reserve(n);for (size_t i = 0; i < n; i++){_vertexs.push_back(a[i]);//存放顶点_IndexMap[a[i]] = i;//存放顶点,并建立顶点与下标的映射关系}_matrix.resize(n);for (int i = 0; i < _matrix.size(); i++){_matrix[i].resize(n, MAX);}}size_t GetIndexMap(const V& v){auto it = _IndexMap.find(v);if (it != _IndexMap.end())return it->second;else{return -1;}}void AddEdge(const V& src, const V& dst, const W& w){size_t srci = GetIndexMap(src);size_t dsti = GetIndexMap(dst);_matrix[srci][dsti] = w;if (Direction == false){_matrix[dsti][srci] = w;}}void BFS(const V& v){size_t scr = GetIndexMap(v);queue<int> q;vector<bool> visited(_vertexs.size(), false);visited[scr] = true;q.push(scr);size_t n = _vertexs.size();while (!q.empty()){size_t front = q.front();q.pop();cout << front << ":" << _vertexs[front] << endl;for (size_t i = 0; i < n; i++){if (_matrix[front][i] != MAX){if (visited[i] == false){q.push(i);visited[i] = true;}}}}}void Print(){cout <<" ";for (size_t i = 0; i < _vertexs.size(); i++){printf("%4d", i);}cout << endl;for (size_t i = 0; i < _matrix.size(); i++){cout << i << ' ';for (size_t j = 0; j < _matrix[i].size(); j++){if (_matrix[i][j] == MAX)printf("%4c", '&');elseprintf("%4d", _matrix[i][j]);}cout << endl;}}private:vector<V> _vertexs;//顶点集map<V,int> _IndexMap;//下标和顶点映射关系vector<vector<W>> _matrix;//邻接矩阵};void test1(){Graph<char, int, INT_MAX, false> g("0123", 4);g.AddEdge('0', '0', 1);g.AddEdge('1', '1', 2);g.AddEdge('2', '2', 3);g.AddEdge('3', '3', 4);g.Print();}void BDFStest(){string a[] = { "张三", "李四", "王五", "赵六" };Graph<string, int, true> g1(a, 4);g1.AddEdge("张三", "李四", 100);g1.AddEdge("张三", "王五", 200);g1.AddEdge("王五", "赵六", 30);g1.Print();g1.BFS("张三");}
}
效果如下:
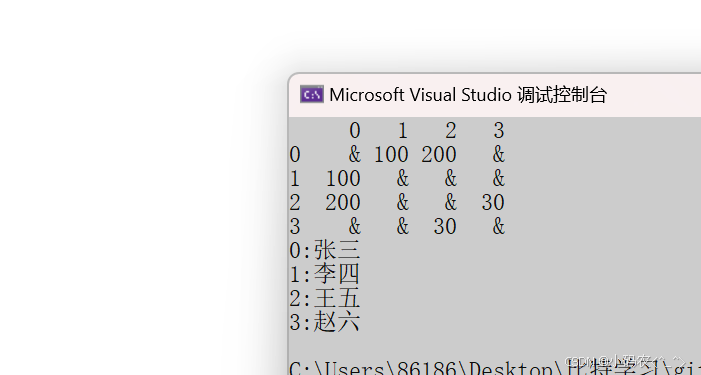
后面的深度优先遍历下一节继续,原因是因为这一部分挺难的,大家其实需要花很多时间去理解一下,总的来说图需要我们画很多精力去学习,相信学懂这一部分不光在代码能力上有很大提升,在逻辑思维也会有很大提升的。
相关文章:

高阶数据结构--图(graph)
图(graph) 1.并查集1. 并查集原理2. 并查集实现3. 并查集应用 2.图的基本概念3. 图的存储结构3.1 邻接矩阵3.2 邻接矩阵的代码实现3.3 邻接表3.4 邻接表的代码实现 4. 图的遍历4.1 图的广度优先遍历4.2 广度优先遍历的代码 1.并查集 1. 并查集原理 在一…...
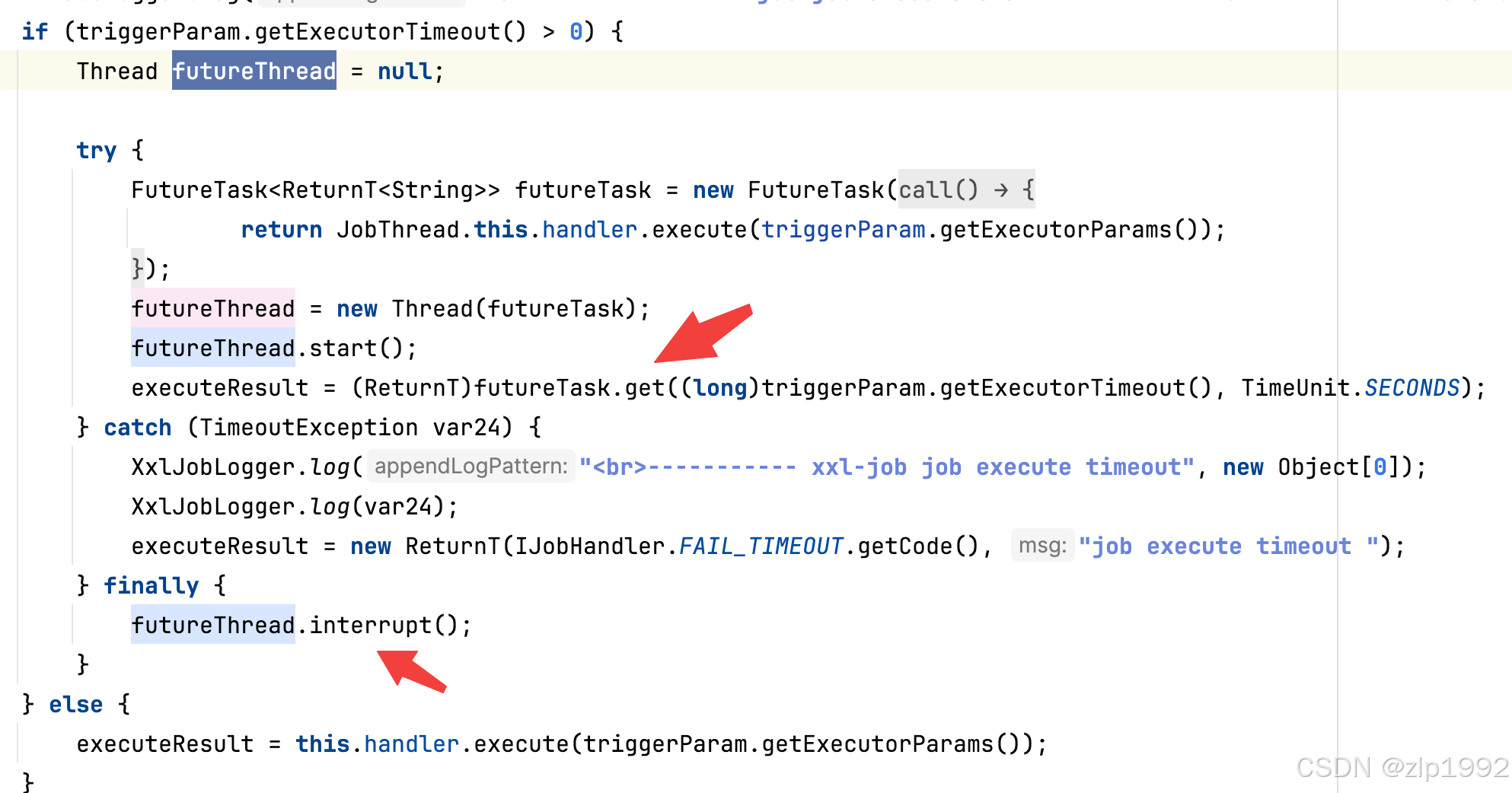
xxl-job java.sql.SQLException: interrupt问题排查
近期生产环境固定凌晨报错,提示 ConnectionManager [Thread-23069] getWriteConnection db:***,pattern: error, jdbcUrl: jdbc:mysql://***:3306/***?connectTimeout3000&socketTimeout180000&autoReconnecttrue&zeroDateTimeBehaviorCONVERT_TO_NUL…...
jmeter压测工具环境搭建(Linux、Mac)
目录 java环境安装 1、anaconda安装java环境(推荐) 2、直接在本地环境安装java环境 yum方式安装jdk 二进制方式安装jdk jmeter环境安装 1、jmeter单机安装 启动jmeter 配置环境变量 jmeter配置中文 2、jmeter集群搭建 多台机器部署jmeter集群…...

docker设置加速
sudo tee /etc/docker/daemon.json <<-‘EOF’ { “registry-mirrors”: [ “https://register.liberx.info”, “https://dockerpull.com”, “https://docker.anyhub.us.kg”, “https://dockerhub.jobcher.com”, “https://dockerhub.icu”, “https://docker.awsl95…...

使用requestAnimationFrame写防抖和节流
debounce.ts 防抖工具函数: function Animate() {this.timer null; }Animate.prototype.start function (fn) {if (!fn) {throw new Error(需要执行函数);}if (this.timer) {this.stop();}this.timer requestAnimationFrame(fn); }Animate.prototype.stop function () {i…...

Puppeteer 与浏览器版本兼容性:自动化测试的最佳实践
Puppeteer 支持的浏览器版本映射:从 v20.0.0 到 v23.6.0 自 Puppeteer v20.0.0 起,这个强大的自动化库开始支持与 Chrome 浏览器的无头模式和有头模式共享相同代码路径,为自动化测试带来了更多便利。从 v23.0.0 开始,Puppeteer 进…...

Java方法重写
在Java中,方法重写是指在子类中重新定义父类中已经定义的方法。以下是Java方法重写的基本原则: 子类中的重写方法必须具有相同的方法签名(即相同的方法名、参数类型和返回类型)。子类中的重写方法不能比父类中的原方法具有更低的…...
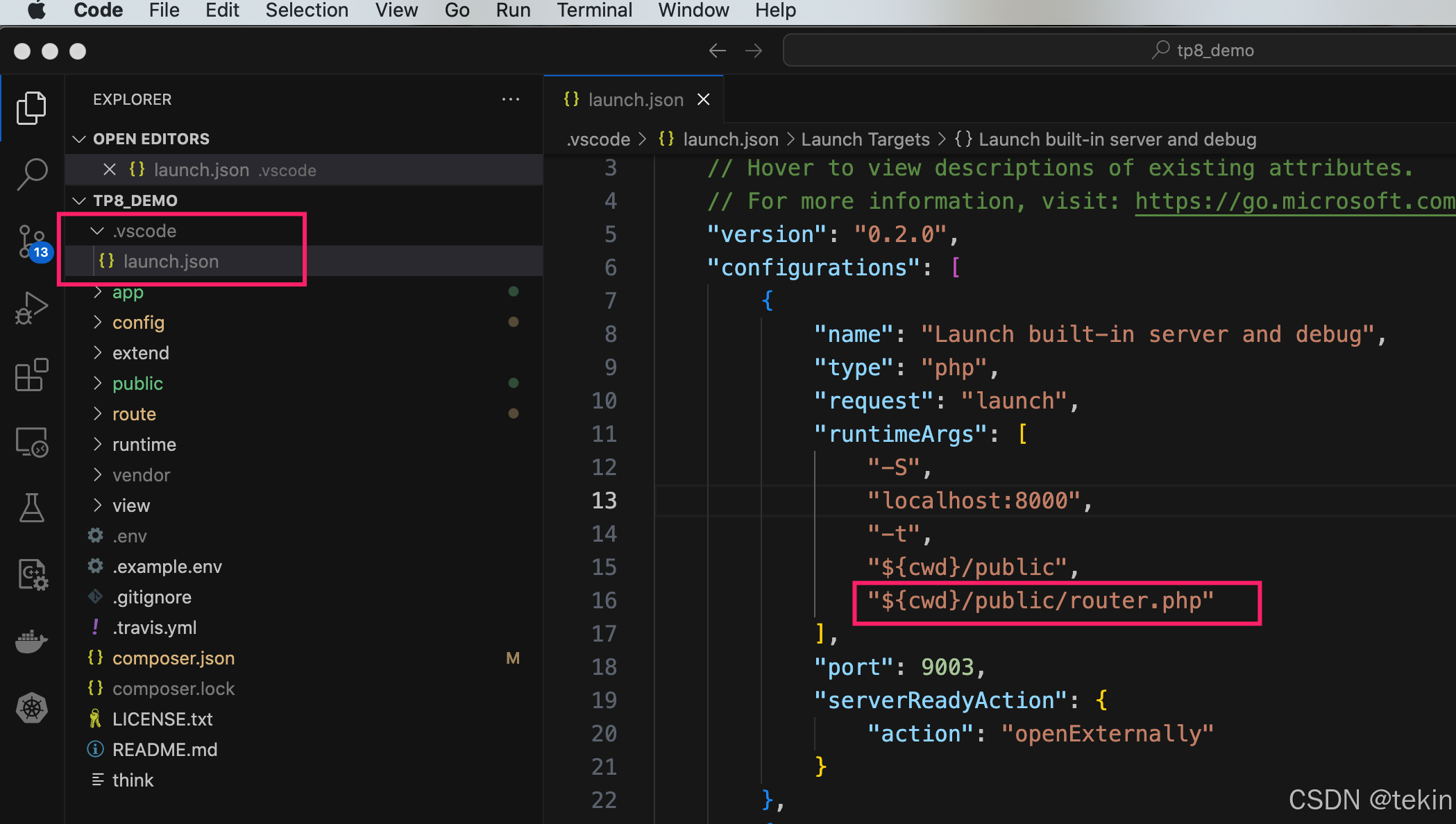
vscode通过.vscode/launch.json 内置php服务启动thinkphp 应用后无法加载路由解决方法
我们在使用vscode的 .vscode/launch.json Launch built-in server and debug 启动thinkphp应用后默认是未加载thinkphp的路由文件的, 这个就导致了,某些thinkphp的一些url路由无法访问的情况, 如http://0.0.0.0:8000/api/auth.admin/info这…...
Webserver(2.6)有名管道
目录 有名管道有名管道使用有名管道的注意事项读写特性有名管道实现简单版聊天功能拓展:如何解决聊天过程的阻塞 有名管道 可以用在没有关系的进程之间,进行通信 有名管道使用 通过命令创建有名管道 mkfifo 名字 通过函数创建有名管道 int mkfifo …...
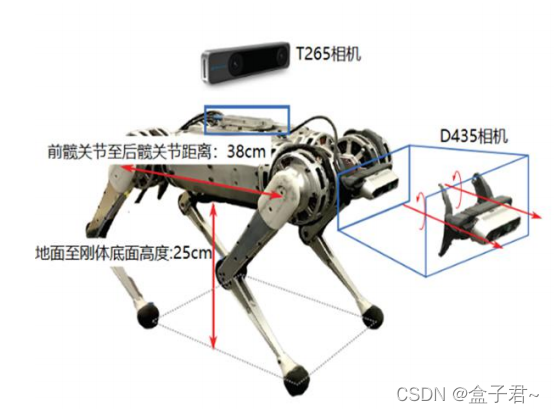
四足机器人实战篇之一:波士顿spot机器人工程实现分析
系列文章目录 提示:这里可以添加系列文章的所有文章的目录,目录需要自己手动添加 TODO:写完再整理 文章目录 系列文章目录前言一、机器人发展历史二、硬件系统及电机执行器篇硬件系统电机执行器传感器机处理器电气连接三、感知(视觉点云、局部地图、定位)篇1.深度相机获取…...

TensorFlow 预训练目标检测模型集合
Tensorflow 提供了一系列在不同数据集上预训练的目标检测模型,包括 COCO 数据集、Kitti 数据集、Open Images 数据集、AVA v2.1 数据集、iNaturalist 物种检测数据集 和 Snapshot Serengeti 数据集。这些模型可以直接用于推理,特别是当你对这些数据集中已…...

字符串的区别
C 和 Java 字符串的区别 最近 C 和 Java 在同步学习,都有个字符串类型,但二者不太一样,于是就做了些许研究。 在编程中,字符串作为数据类型广泛应用于不同的场景。虽然 C 和 Java 都允许我们处理字符串,但它们在字符…...

EMR Serverless Spark:一站式全托管湖仓分析利器
本文根据2024云栖大会实录整理而成,演讲信息如下: 演讲人: 李钰(绝顶) | 阿里云智能集团资深技术专家,阿里云 EMR 团队负责人 活动: 2024 云栖大会 AI - 开源大数据专场 数据平台技术演变 …...

Linux find 匹配文件内容
在Linux中,你可以使用find命令结合-exec或者-execgrep来查找匹配特定内容的文件。以下是一些示例: 查找当前目录及其子目录下所有文件内容中包含"exampleText"的文件: find . -type f -exec grep -l "exampleText" {} \…...
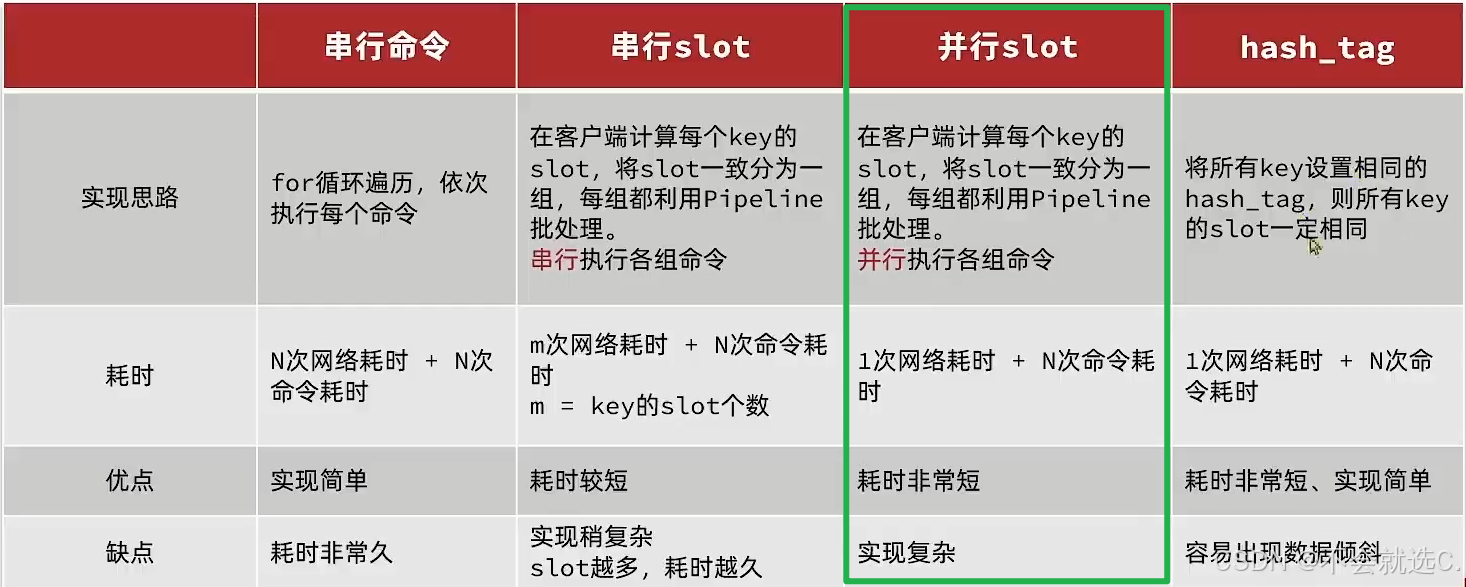
【Redis优化——如何优雅的设计key,优化BigKey,Pipeline批处理Key】
Redis优化——如何优雅的设计key,优化BigKey,Pipeline批处理Key 一、Key的设计1. 命名规范2. 长度限制在44字节以内 二、BigKey优化1. 查找bigkey2. 删除BigKey3. 优化BigKey 三、Pipeline批处理Key1. 单节点的Pipeline2. 集群下的Pipeline 一、Key的设计…...
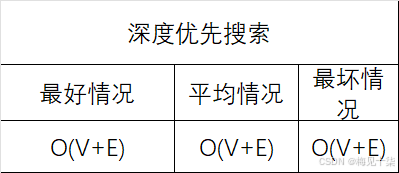
数据结构与算法分析:你真的理解图算法吗——深度优先搜索(代码详解+万字长文)
一、前言 图是计算机科学中用来表示复杂结构信息的一种基本结构。本章我们会讨论一些通用的围表示法,以及一些频繁使用的图算法。本质上来说,一个图包含一个元素集合(也就是顶点),以及元素两两之间的关系(也就是边),由于应用范围所限,本章我们仅仅讨论简单图,简单围并不会如(a…...
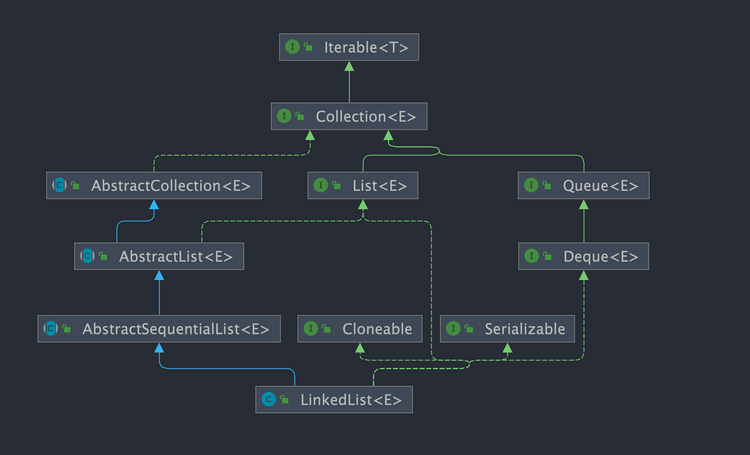
LinkedList 分析
LinkedList 简介 LinkedList 是一个基于双向链表实现的集合类,经常被拿来和 ArrayList 做比较。关于 LinkedList 和ArrayList的详细对比,我们 Java 集合常见面试题总结(上)有详细介绍到。 双向链表 不过,我们在项目中一般是不会使用到 Link…...
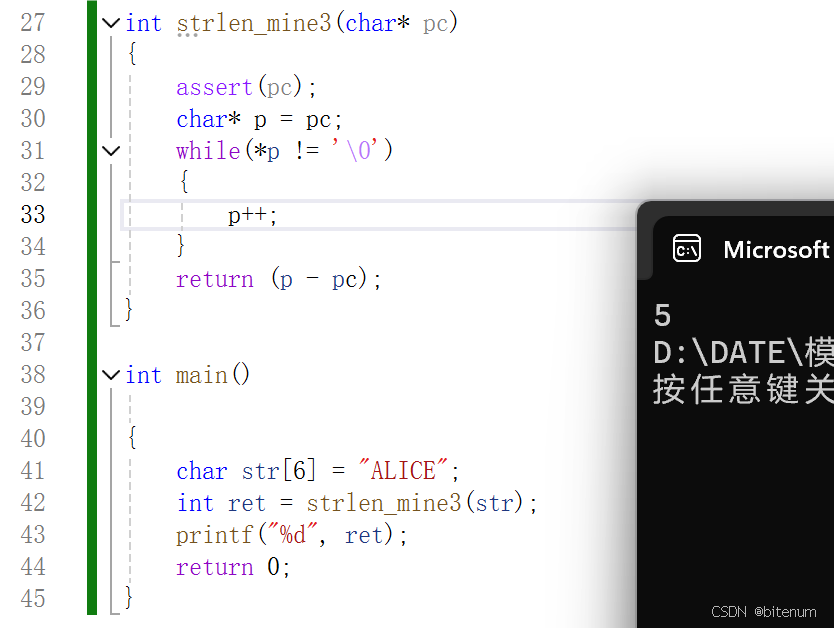
【C/C++】模拟实现strlen
学习目标: 使用代码模拟实现strlen。 逻辑: strlen 需要输入一个字符串数组类型的变量,并且返回一个整型类型的数据。strlen 需要计算字符串数组有多少个元素。 代码1:使用计数器 #define _CRT_SECURE_NO_WARNINGS 1 #include&…...
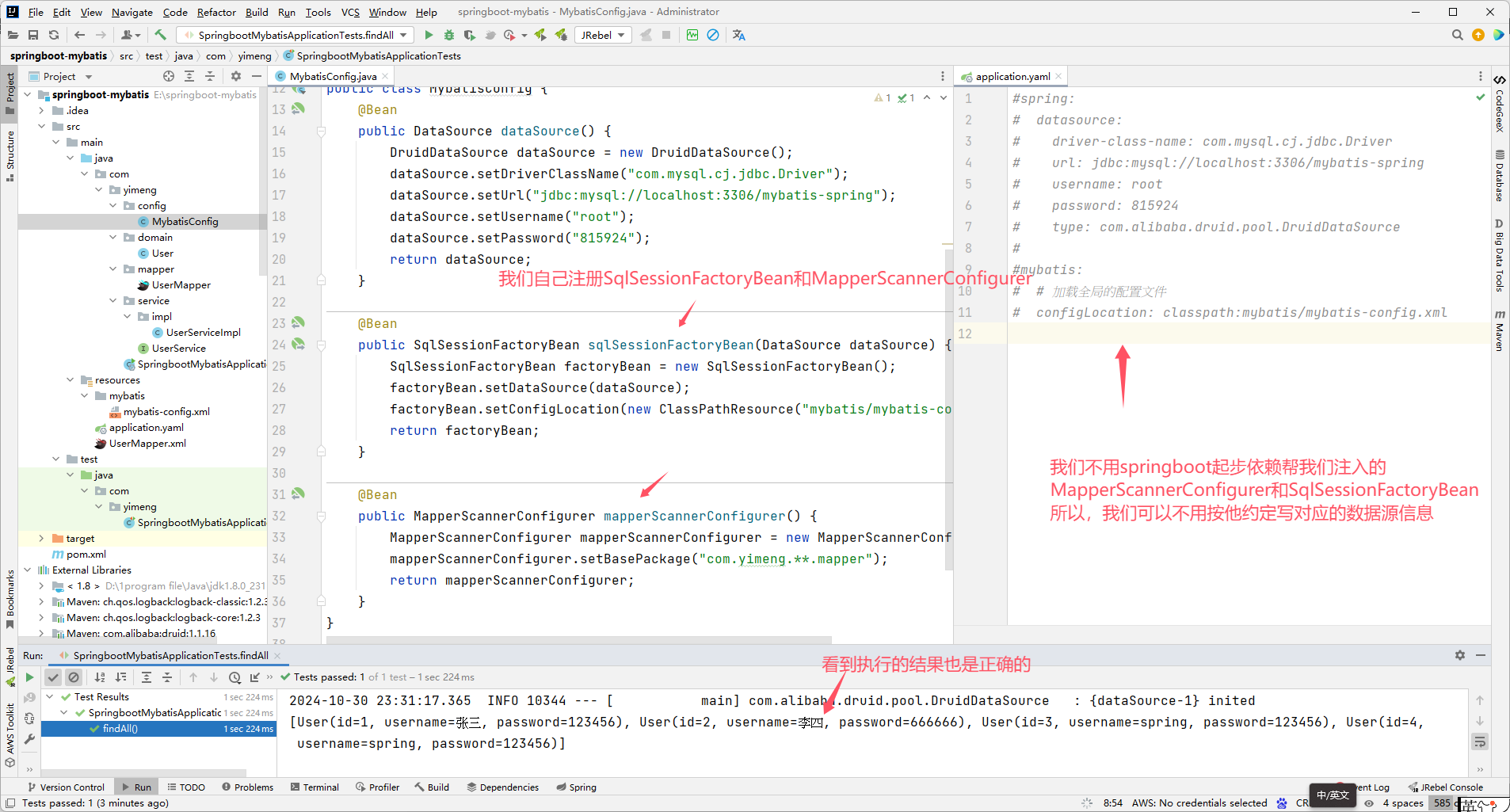
mybatis从浅入深一步步演变分析
mybatis从浅入深一步步演变分析 版本一:不使用代理(非spring) package com.yimeng.domain;public class User {private int id;private String username;private String password;public int getId() {return id;}public void setId(int id…...
Java阶段三02
第3章-第2节 一、知识点 面向接口编程、什么是spring、什么是IOC、IOC的使用、依赖注入 二、目标 了解什么是spring 理解IOC的思想和使用 了解IOC的bean的生命周期 理解什么是依赖注入 三、内容分析 重点 了解什么是spring 理解IOC的思想 掌握IOC的使用 难点 理解IO…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

Mysql中select查询语句的执行过程
目录 1、介绍 1.1、组件介绍 1.2、Sql执行顺序 2、执行流程 2.1. 连接与认证 2.2. 查询缓存 2.3. 语法解析(Parser) 2.4、执行sql 1. 预处理(Preprocessor) 2. 查询优化器(Optimizer) 3. 执行器…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...
