非线性数据结构之数
一、基本概念
1. 二叉树的节点与深度
- 节点:二叉树的基本组成单位,每个节点包含一个数据值、一个左子节点和一个右子节点。
- 树的深度(Height):指树的根节点到叶子节点的最长路径所包含的边数。
2. 二叉树的类型
- 叶节点:没有子节点的节点。
- 内部节点:具有子节点的节点。
二、二叉树的种类
1. 完全二叉树(Complete Binary Tree)
定义:完全二叉树的所有层都被完全填满,除了最后一层的节点必须自左向右排列。
特点:
- 通常使用数组实现,具有简洁的内存结构,且方便通过索引访问。
- 节点索引公式:若根节点为第 0 个元素,则节点 i 的左子节点索引为 2i + 1,右子节点为 2i + 2,父节点为 (i-1) / 2。
优缺点:
- 优点:提高了存储和遍历的效率,常用于实现堆。
- 缺点:对树的结构有严格要求,插入和删除操作需要维护完全性。
应用:常见于堆排序、优先队列实现等。
2. 满二叉树(Full Binary Tree)
定义:每个节点都有两个子节点,且所有叶节点的深度相同。
特点:
- 所有层都被完全填满,节点数达到最大。
- 满二叉树的节点数 n 与深度 h 满足公式:n = 2^(h+1) - 1。
优缺点:
- 优点:结构紧凑,便于平衡和遍历。
- 缺点:插入和删除操作较为不便,需维持每层的完整性。
应用:常用于存储静态数据,或需要完全对称的数据结构中。
3. 二叉搜索树(Binary Search Tree, BST)
定义:BST 是一种特殊的二叉树,满足以下性质:
- 若左子树不为空,则左子树上所有节点的值均小于根节点的值。
- 若右子树不为空,则右子树上所有节点的值均大于根节点的值。
- 左右子树均为二叉搜索树。
特点:
- 支持平均 O(log n) 的插入、删除和查找操作。
- 中序遍历 BST 可获得有序序列。
优缺点:
- 优点:查找和修改操作效率高,适合动态数据集。
- 缺点:在极端情况下(如插入数据有序),树可能会退化为链表,导致性能下降到 O(n)。
应用:用于数据库索引、文件系统、字典等。
示例代码(Java):
class TreeNode {int value;TreeNode left;TreeNode right;TreeNode(int value) {this.value = value;}
}class BinarySearchTree {TreeNode root;// 插入public void insert(int value) {root = insertRecursive(root, value);}private TreeNode insertRecursive(TreeNode node, int value) {if (node == null) {return new TreeNode(value);}if (value < node.value) {node.left = insertRecursive(node.left, value);} else if (value > node.value) {node.right = insertRecursive(node.right, value);}return node;}// 查找public boolean search(int value) {return searchRecursive(root, value);}private boolean searchRecursive(TreeNode node, int value) {if (node == null) {return false;}if (value == node.value) {return true;} return value < node.value ? searchRecursive(node.left, value) : searchRecursive(node.right, value);}
}
三、平衡树
定义
平衡树是一种保持树结构平衡的二叉树,通常限制了节点的高度差异,使得查找、插入和删除操作保持在 O(log n) 的时间复杂度。
特点:平衡树通常通过旋转操作来调整子树的高度,从而防止极端情况导致的退化。
1. AVL 树
定义:AVL 树是一种自平衡二叉搜索树,具有以下性质:
- 每个节点的左右子树高度差最多为 1。
特点:
- 通过“旋转”操作(单旋、双旋)在插入和删除节点后重新平衡树。
- 查找、插入、删除操作复杂度均为 O(log n)。
优缺点:
- 优点:严格平衡,查找效率较高。
- 缺点:旋转操作较多,插入和删除效率较低。
应用:适用于查找频繁、插入删除较少的场景,如数据库索引。
2. 红黑树(Red-Black Tree)
定义:红黑树是一种二叉搜索树,具有以下性质:
- 节点为红色或黑色。
- 根节点为黑色。
- 红节点的子节点必须为黑色(红节点不能相邻)。
- 从根节点到叶节点的每条路径都包含相同数目的黑节点。
特点:
- 通过颜色和旋转操作来维持平衡。
- 查找、插入、删除操作平均时间复杂度为 O(log n)。
优缺点:
- 优点:插入和删除效率高,适合频繁修改的数据。
- 缺点:实现复杂。
应用:常见于 Java 的 TreeMap、C++ 的 map,适用于需要快速插入和删除的应用。
3. Splay 树
定义:Splay 树是一种自调整二叉搜索树,最近访问的节点将旋转至根节点。这样更常用的元素将接近根节点,减少平均查找时间。
特点:
- 最近使用的数据靠近根节点,提高局部访问效率。
- 每次查找、插入或删除操作都会将目标节点旋转至根节点。
优缺点:
- 优点:适合高频访问的数据。
- 缺点:单次操作复杂度较高,不适合随机访问。
应用:缓存、文件系统等需要频繁访问某些节点的数据结构。
4. 比较总结
| 树种类 | 平衡方式 | 优点 | 缺点 | 适用场景 |
|---|---|---|---|---|
| AVL 树 | 左右子树高度差平衡 | 查找效率高 | 插入、删除操作复杂 | 查找频繁,变动少的数据集 |
| 红黑树 | 颜色与旋转 | 插入、删除效率高 | 实现复杂 | Java 的 TreeMap、Linux VFS |
| Splay 树 | 自调整,最近访问至根 | 适合频繁访问的数据结构 | 随机访问不高效 | 缓存、需要局部访问的系统 |
这些平衡树结构适用于不同的场景,各有优缺点。在实际应用中根据需求选择适合的平衡树可以显著提高数据结构的操作效率。
相关文章:

非线性数据结构之数
一、基本概念 1. 二叉树的节点与深度 节点:二叉树的基本组成单位,每个节点包含一个数据值、一个左子节点和一个右子节点。树的深度(Height):指树的根节点到叶子节点的最长路径所包含的边数。 2. 二叉树的类型 叶节…...

个人开发三步走
一、开发准备 1.需求分析:需求是开发的起点。第一步要做的就是明确需求,具体来说就是分析目标用户、他们的需求(功能需求、性能需求、安全需求)和痛点。 2.技术选型:综合开发需求、个人能力(能熟练使用&a…...

qt QAction详解
1、概述 QAction是Qt框架中的一个抽象类,用于表示用户界面中的一个动作(action)。这些动作可以绑定到菜单项、工具栏按钮或快捷键上,提供了一种灵活的方式来处理用户交互。QAction不仅包含了动作的名称、图标、提示信息等属性&am…...

建立maven项目常见问题解决办法
从git拉的项目爆红 https://blog.csdn.net/wsdbld_/article/details/115380325 idea点击具体的类没有反应 https://www.likecs.com/show-204943934.html maven Could not find artifact com.** 无法下载原因分析 https://www.cnblogs.com/thinkingandworkinghard/p/100824…...

Windows 10 安装使用Docker踩过的坑和解决-31/10/2024
目录 环境版本 一、Docker Desktop双击启动没反应,open //./pipe/dockerDesktopLinuxEngine: The system cannot find the file specified. 二、Docker Desktop运行run命令时显示错误HTTP code 500 并且错误大意是服务器拒绝访问 三、Docker Engine stopped/启动…...

微服务之间的调用关系
从数据的流向来区分有 1.直接调用(推)A直接B的接口直接将数据推送给B; 2.间接调用(拉)A先调B,B根据A给信息再去调A拉取数据; 感觉间接调用有点多此一举!!! 直接调用的…...

Chinese Spelling Correction as Rephrasing Language Model(AAAI2024)
Chinese Spelling Correction as Rephrasing Language Model(AAAI2024) 一.概述 目前最先进的方法将CSC(Chinese Spelling Correction)作为序列标注任务,并在句子对上微调基于bert的方法。然而,我们注意到在将一个字符标注为另一个字符的过…...
)
DirectShow过滤器开发-写MP3音频文件过滤器(再写 写MP3)
下载本过滤器DLL 本过滤器将MP3音频流写到MP3音频文件。 过滤器信息 过滤器名称:写MP3_2 过滤器GUID:{AE46BC15-71E5-471C-8540-3B73094111EC} DLL注册函数名:DllRegisterServer 删除注册函数名:DllUnregisterServer 过滤器有1个…...
文章解读与仿真程序复现思路——电力自动化设备EI\CSCD\北大核心《基于对等架构的虚拟电厂-配电网双层电碳协同调度模型》
本专栏栏目提供文章与程序复现思路,具体已有的论文与论文源程序可翻阅本博主免费的专栏栏目《论文与完整程序》 论文与完整源程序_电网论文源程序的博客-CSDN博客https://blog.csdn.net/liang674027206/category_12531414.html 电网论文源程序-CSDN博客电网论文源…...

大数据-204 数据挖掘 机器学习理论 - 混淆矩阵 sklearn 决策树算法评价
点一下关注吧!!!非常感谢!!持续更新!!! 目前已经更新到了: Hadoop(已更完)HDFS(已更完)MapReduce(已更完&am…...

Fsm1
为了处理有时间上先后的事件,在FPGA中采用状态机的形式完成事件处理。 Mealy 状态机:输出不仅取决于当前状态,还取决于输入状态。 Moore 状态机:组合逻辑的输出只取决于当前状态,而与输入状态无关。 二段式状态机&…...

C. Gorilla and Permutation
time limit per test 2 seconds memory limit per test 256 megabytes Gorilla and Noobish_Monk found three numbers nn, mm, and kk (m<km<k). They decided to construct a permutation†† of length nn. For the permutation, Noobish_Monk came up with the …...

从0开始学python-day17-数据结构2
2.3 队列 队列(Queue),它是一种运算受限的线性表,先进先出(FIFO First In First Out) 队列是一种受限的线性结构 受限之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作 P…...
—— 编程基础)
(蓝桥杯C/C++)—— 编程基础
文章目录 一、C基础格式 1.打印hello, world 2.基本数据类型 二、string 1.string简介 2.string的声明和初始化 3.string其他基本操作 (1)获取字符串长度 (2) 拼接字符串( 或 append) (3)字符串查找(find) (4)字符串替换 (5)提取子字符串…...
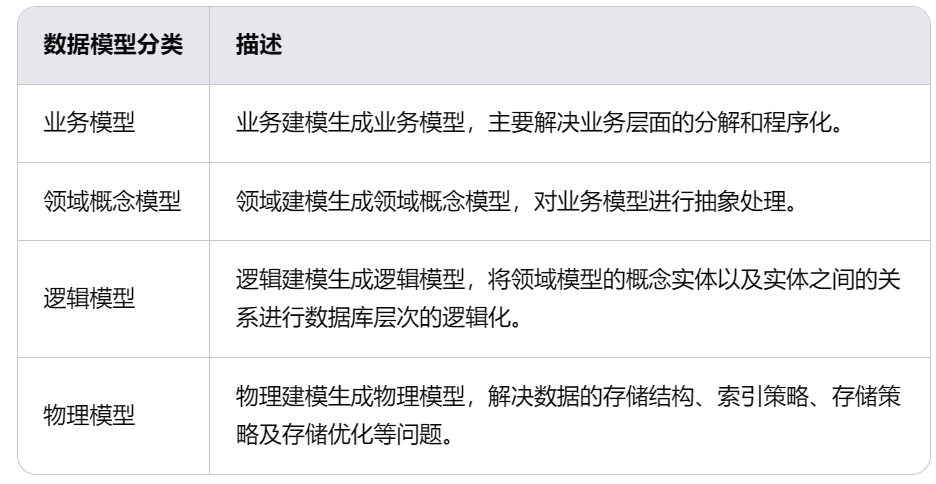
企业物流管理数据仓库建设的全面指南
文章目录 一、物流管理目标二、总体要求三、数据分层和数据构成(1)数据分层(2)数据构成 四、数据存储五、数据建模和数据模型(1)数据建模(2)数据模型 六、总结 在企业物流管理中&…...

数据采集-Kepware 安装证书异常处理
这里写目录标题 一、 问题描述二、原因分析三、处理方案3.1 1.执行根证书的更新3.2 安装KepServerEx 资源 一、 问题描述 在进行KepServerEx进行安装的情况下,出现了如下的报错: The installer was unable to find required root certificates ,please …...

ubuntu禁止自动更新设置
背景概述 从CentOS变更到uBuntu或多或少会遇到一些坑,今天分享一个。 在Ubuntu系统中,自动更新是一个既方便又引发争议的功能。它可以帮助用户保持系统的最新状态,但有时也会因为自动更新而导致系统不稳定或不兼容。 Ubuntu系统的自动更新主…...

Rust 力扣 - 1461. 检查一个字符串是否包含所有长度为 K 的二进制子串
文章目录 题目描述题解思路题解代码题目链接 题目描述 题解思路 长度为k的二进制子串所有取值的集合为[0, sum(k)],其中sum(k)为1 2 4 … 1 << (k - 1) 我们只需要创建一个长度为sum(k) 1的数组 f ,其中下标为 i 的元素用来标记字符串中子串…...
C#/.NET/.NET Core技术前沿周刊 | 第 11 期(2024年10.21-10.31)
前言 C#/.NET/.NET Core技术前沿周刊,你的每周技术指南针!记录、追踪C#/.NET/.NET Core领域、生态的每周最新、最实用、最有价值的技术文章、社区动态、优质项目和学习资源等。让你时刻站在技术前沿,助力技术成长与视野拓宽。 欢迎投稿、推荐…...

unity 三维数学 ,角度 弧度计算
弧度 角度*π/180...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

淘宝扭蛋机小程序系统开发:打造互动性强的购物平台
淘宝扭蛋机小程序系统的开发,旨在打造一个互动性强的购物平台,让用户在购物的同时,能够享受到更多的乐趣和惊喜。 淘宝扭蛋机小程序系统拥有丰富的互动功能。用户可以通过虚拟摇杆操作扭蛋机,实现旋转、抽拉等动作,增…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...
