AcWing1077-cnblog
问题背景
给定一个树形结构的图,每个节点代表一个地点,每个节点有一个守卫的代价。我们希望以最低的代价在树的节点上放置守卫,使得整棵树的所有节点都被监控。可以通过三种方式覆盖一个节点:
- 由父节点监控。
- 由子节点监控。
- 自己放置一个守卫监控自己。
状态表示
定义 $ f[i][k] $ 为第 $ i $ 个节点在状态 $ k $ 下的最小代价,其中状态 $ k $ 有三种取值:
- $ f(i, 0) $:第 $ i $ 号节点由父节点的守卫监控的方案数。
- $ f(i, 1) $:第 $ i $ 号节点由子节点的守卫监控的方案数。
- $ f(i, 2) $:第 $ i $ 号节点自己放置守卫监控自己的方案数。
状态转移方程
根据题意和约束条件,通过递归计算以下三种状态的最小代价:
-
父节点监控 $ f(i, 0) $:节点 $ i $ 被父节点监控,则每个子节点 $ j $ 要么自己监控自己(状态 $ f(j, 2) $),要么被它的子节点监控(状态 $ f(j, 1) $)。
f ( i , 0 ) = ∑ min ( f ( j , 1 ) , f ( j , 2 ) ) f(i, 0) = \sum \min(f(j,1), f(j,2)) f(i,0)=∑min(f(j,1),f(j,2)) -
子节点监控 $ f(i, 1) $:节点 $ i $ 被一个子节点监控。我们要枚举是哪一个子节点 $ k $ 来监控 $ i $,然后在所有方案中取最小值。
f ( i , 1 ) = min k { f ( i , 0 ) + f ( k , 2 ) − min ( f ( k , 1 ) , f ( k , 2 ) ) } f(i, 1) = \min_{k} \{ f(i, 0) + f(k, 2) - \min(f(k,1), f(k,2)) \} f(i,1)=kmin{f(i,0)+f(k,2)−min(f(k,1),f(k,2))}
其中, $ f(i, 0) $ 中包含了所有子节点的最小监控代价之和,这里要去除子节点 $ k $ 的原代价,替换成状态 $ f(k, 2) $(即子节点 $ k $ 自己监控自己)。 -
自我监控 $ f(i, 2) $:节点 $ i $ 自己放置守卫,则所有子节点 $ j $ 可以选择任意一种监控方案:由父节点监控、自己监控或由子节点监控。
f ( i , 2 ) = ∑ min ( f ( j , 0 ) , f ( j , 1 ) , f ( j , 2 ) ) + w ( i ) f(i, 2) = \sum \min(f(j,0), f(j,1), f(j,2)) + w(i) f(i,2)=∑min(f(j,0),f(j,1),f(j,2))+w(i)
其中, $ w(i) $ 表示在节点 $ i $ 放置守卫的代价。
算法流程
- 建树:使用邻接表存储树结构,使用
add函数建立节点之间的连接。 - 找到根节点:在输入数据中标记所有有父节点的节点,剩下未标记的节点即为根节点。
- 深度优先搜索 (DFS):从根节点开始递归遍历树,计算每个节点的三种状态的最小代价。
- 结果输出:最终输出根节点的两种监控方案中的最小代价,即
min(f[root][1], f[root][2])。
代码中的核心部分
dfs(int u):递归计算每个节点在三种状态下的最小代价。利用递归遍历树的结构,自底向上地计算各个状态的代价。add(int a, int b):构建树的邻接表表示,用于方便地遍历子节点。- 状态初始化和递推公式的应用:在 DFS 的过程中,不断更新和计算
f[u][0],f[u][1],f[u][2]。
复杂度分析
由于是树形结构的遍历,算法的时间复杂度为 $ O(N) $,其中 $ N $ 是节点数。空间复杂度同样是 $ O(N) $,主要用于存储树的结构和每个节点的三种状态的代价。
总结
-
这个算法有效利用了树的层次结构和动态规划的递推思想,通过状态转移和自底向上的动态规划求解每个节点的最小监控方案。
-
状态设计和转移公式充分考虑了监控的三种情况,通过分解为子问题并合并结果,实现了最优代价的计算。
-
状态设计和转移公式充分考虑了监控的三种情况,通过分解为子问题并合并结果,实现了最优代价的计算。
这段代码是一个典型的树形动态规划问题的解法,适用于解决诸如最小路径覆盖、监控覆盖等类似的树结构上的最小代价问题。
相关文章:

AcWing1077-cnblog
问题背景 给定一个树形结构的图,每个节点代表一个地点,每个节点有一个守卫的代价。我们希望以最低的代价在树的节点上放置守卫,使得整棵树的所有节点都被监控。可以通过三种方式覆盖一个节点: 由父节点监控。由子节点监控。自己…...
)
五、SpringBoot3实战(1)
一、SpringBoot3介绍 1.1 SpringBoot3简介 SpringBoot版本:3.0.5 https://docs.spring.io/spring-boot/docs/current/reference/html/getting-started.html#getting-started.introducing-spring-boot 到目前为止,你已经学习了多种配置Spring程序的方式…...

练习LabVIEW第三十三题
学习目标: 刚学了LabVIEW,在网上找了些题,练习一下LabVIEW,有不对不好不足的地方欢迎指正! 第三十三题: 用labview编写一个判断素数的程序 开始编写: LabVIEW判断素数,首先要搞…...
如何在服务器端对PDF和图像进行OCR处理
介绍 今天我想和大家分享一个我在研究技术资料时发现的很好玩的东西——Tesseract。这不仅仅是一个普通的库,而是一个用C语言编写的OCR神器,能够识别一大堆不同国家的语言。我一直在寻找能够处理各种文档的工具,而Tesseract就像是给了我一把…...

Windows 下实验视频降噪算法 MeshFlow 详细教程
MeshFlow视频降噪算法 Meshflow 视频降噪算法来自于 2017 年电子科技大学一篇高质量论文。 该论文提出了一个新的运动模型MeshFlow,它是一个空间平滑的稀疏运动场 (spatially smooth sparse motion field),其运动矢量 (motion vectors) 仅在网格顶点 (m…...

Python入门:如何正确的控制Python异步并发量(制并发量的关键技巧与易错点解析)
文章目录 📖 介绍 📖🏡 演示环境 🏡📒 异步并发量控制 📒📝 Python异步并发简介📝 为什么要限制并发量🎈 资源管理🎈 服务稳定性📝 新手容易犯的错误🎈 忽略并发量限制🎈 错误设置并发量📝 设置并发量要注意的事情🎈 了解任务类型🎈 考虑系统资…...

qt QCheckBox详解
QCheckBox 是 Qt 框架中的一个控件,用于创建复选框,允许用户进行选择和取消选择。它通常用于表单、设置界面和任何需要用户选择的场景。 QCheckBox继承自QAbstractButton类,因此继承了按钮的特性。它表示一个复选框,用户可以通过…...

PAT甲级-1041 Be Unique
题目 题目大意 从一组数字中选出第一个唯一出现的数,输出该数。如果没有,则输出None。 思路 哈希的思想,将数值作为索引,对应该数值出现的次数,然后遍历数组即可。 注意第一个数字是指数字的个数,不是数…...

【jvm】如何设置堆内存大小
目录 1. 使用命令行参数设置2. idea中设置3. 注意事项 1. 使用命令行参数设置 1.在Java命令后添加-Xms和-Xmx参数。2.-Xms参数用于设置JVM的初始堆内存大小,等价于-XX:InitialHeapSize。3.-Xmx参数用于设置JVM的最大堆内存大小,等价于-XX:MaxHeapSize。…...

kernel源码分析 do_msgsnd read_msg
笔者分析的源码是v 5.11.22 链接:msg.c - ipc/msg.c - Linux source code v5.11.22 - Bootlin do_msgsnd static long do_msgsnd(int msqid, long mtype, void __user *mtext,size_t msgsz, int msgflg) {struct msg_queue *msq;struct msg_msg *msg;int err;str…...

掌握 CTE 技巧,实现连续日期和月份的 SQL 报表统计
在 SQL 查询中,报表统计往往涉及到特定时间段内的数据汇总,如每日、每月的销售数据等。然而,面对缺少数据的日期或月份,传统 SQL 查询可能会直接跳过这些日期,使得输出的报表在视觉上并不连续。本文将展示如何利用 CTE…...

【表格解决问题】EXCEL行数过多,WPS如何按逐行分别打印多个纸张中
1 问题描述 如图:我的表格行数太多了。打印在一张纸上有点不太好看 2 解决方式 Step01:先选中你需要打印的部分,找到【页面】->【打印区域】->【设置打印区域】 Step02:先选中一行,找到【插入分页符】 Step0…...

Maven讲解从基础到高级配置与实践
一、基础认知 1.1 Maven 的主要作用 Maven 主要是用来管理 Java 项目构建流程的工具,包括以下几个方面: 依赖管理:通过 POM.xml 文件管理项目的外部依赖库,不同版本的依赖包可以通过 Maven 中央仓库自动下载,减少了…...

Vue3组件式父子传值
下面是使用 <script setup> 语法的 Vue 3 组件之间传值的示例。 示例 1:使用 Props 和 Emits 父组件 <template><div><h1>父组件</h1><ChildComponent :message="parentMessage" @reply="handleReply" /><p>…...

网页自动化测试和爬虫:Selenium库入门与进阶
网页自动化测试和爬虫:Selenium库入门与进阶 在现代Web开发和数据分析中,自动化测试和数据采集成为了开发流程中的重要部分。Python 的 Selenium 库是一种强大的工具,不仅用于网页自动化测试,也在网页爬虫中得到了广泛的应用。本…...

Cells 单元
Goto Data Grid 数据网格 Cells 单元 Content Alignment 内容对齐 显示数值的数据网格单元格会将其内容向右对齐。显示其他类型数据的单元格将其内容向左排列。若要更改单元格内容对齐方式,请处理 ColumnView.RowCellDefaultAlignment 事件。 Selection Modes 选…...
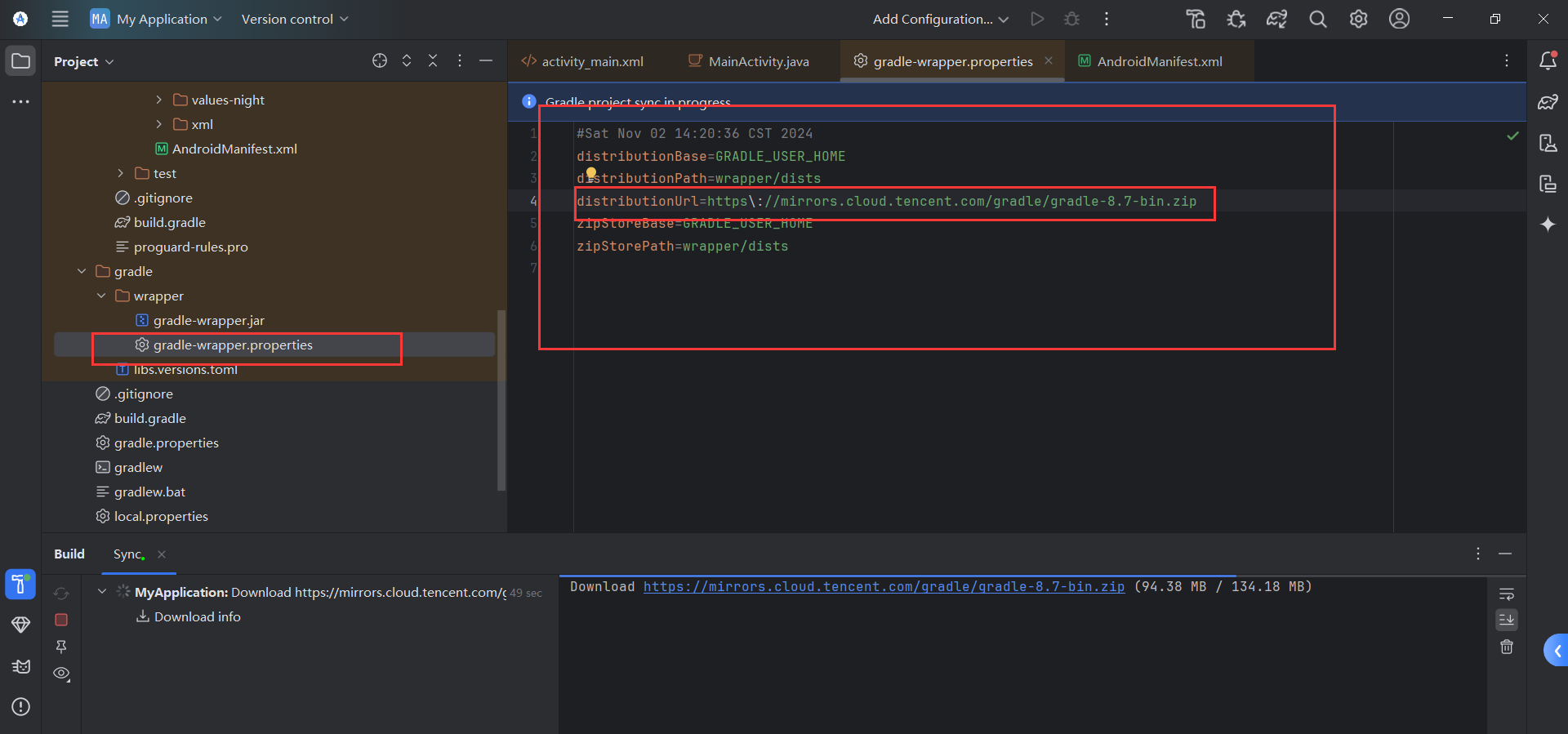
2024/11/2 安卓创建首页界面
Gradle 8.7 bin是指Gradle 8.7版本的二进制包,通常以.zip或.tar.gz格式提供。这个二进制包包含了运行Gradle所需的所有文件,用户可以直接下载并解压使用,无需从源代码编译。 首先了解最常用的布局 线性布局(从上到下&#x…...

SpringSession源码分析
默认对常规Session的理解和使用,如何使用Set-Cookie。 Maven库 常见的spring-session-data-redis依赖spring-session-core <dependency><groupId>org.springframework.session</groupId><artifactId>spring-session-core</artifactId&…...
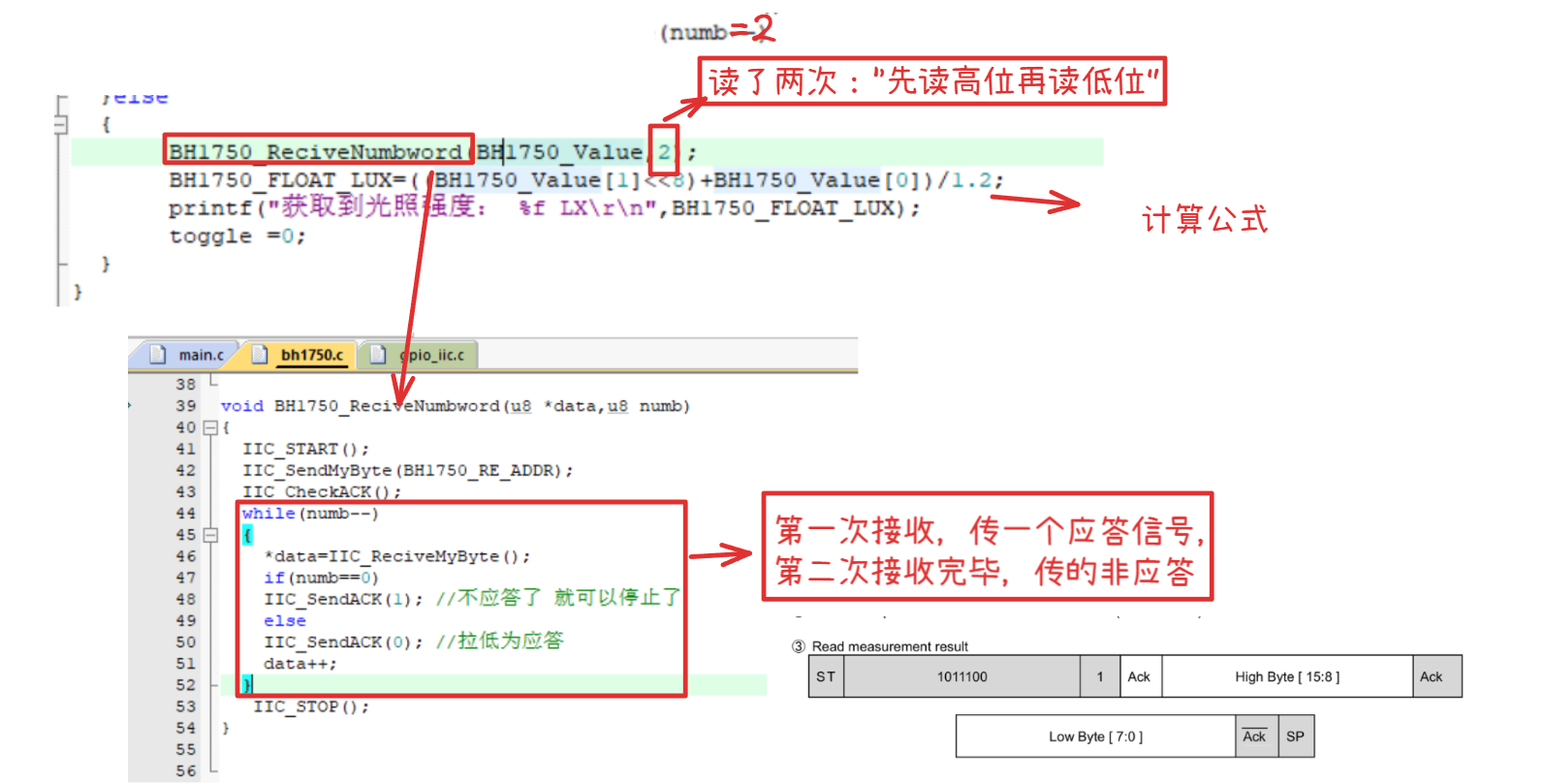
IIC
IIC 目录 IIC BH1750型号的光照传感器 IIC通信协议 iic物理层 IIC软件层协议 -- 那么一主多从,怎么选中与指定的从机通信呢? 从机设备地址 -- 从手册中查看 IIC 写操作 IIC 读操作 硬件IIC和模拟 IIC 使用 模拟 IIC 使用 !&…...

LLM Observability: Azure OpenAI (一)
作者:来自 Elastic Vinay Chandrasekhar•Andres Rodriguez 我们很高兴地宣布 Azure OpenAI 集成现已全面上市,它提供了对 Azure OpenAI 服务性能和使用的全面可观察性!另请参阅本博客的第 2 部分 虽然我们已经提供了对 LLM 环境的可视性一段…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...
