【高中数学】数列
等差数列前 n n n 项和性质
公式一: S n = n ( a 1 + a n ) 2 S_n=\frac{n(a_1+a_n)}{2} Sn=2n(a1+an)
公式二: S n = n a 1 + n ( n − 1 ) 2 d S_n=na_1+\frac{n(n-1)}{2}d Sn=na1+2n(n−1)d
性质1:等差数列中依次 k k k 项之和 S k , S 2 k − S k , S 3 k − S 2 k , . . . S_k,S_{2k}-S_k,S_{3k}-S_{2k},... Sk,S2k−Sk,S3k−S2k,... 组成的数列是公差为 k 2 d k^2d k2d 的等差数列
性质2:若等差数列的项数为 2 n − 1 2n-1 2n−1,则 S 2 n − 1 = ( 2 n − 1 ) a n S_{2n-1}=(2n-1)a_n S2n−1=(2n−1)an
性质3: { a n } \{a_n\} {an} 为等差数列 ⇒ { S n n } \Rightarrow \{\frac{S_n}{n}\} ⇒{nSn} 为等差数列
性质4:若 { a n } , { b n } \{a_n\},\{b_n\} {an},{bn} 都为等差数列, S n , T n S_n,T_n Sn,Tn 分别为他们的前 n n n 项和,则 a n b n = S 2 n − 1 T 2 n − 1 \frac{a_n}{b_n}=\frac{S_{2n-1}}{T_{2n-1}} bnan=T2n−1S2n−1
方程思想在等差数列求和中运用很重要, a 1 , d , n , a n , S n a_1,d,n,a_n,S_n a1,d,n,an,Sn 五个元素可以知三求二
事实上, S n n = A ⋅ n + B ⇔ { S n n } \frac{S_n}{n}=A·n+B\Leftrightarrow \big\{\frac{S_n}{n}\big\} nSn=A⋅n+B⇔{nSn} 为等差数列,且有 S m m , S 2 m 2 m , S 3 m 3 m \frac{S_m}{m},\frac{S_{2m}}{2m},\frac{S_{3m}}{3m} mSm,2mS2m,3mS3m 成等差数列
等比数列前 n n n 项和性质
性质1: S m + n = S n + q n S m S_{m+n}=S_n+q^nS_m Sm+n=Sn+qnSm
性质2:若 S k , S 2 k − S k , S 3 k − S 2 k S_k,S_{2k}-S_k,S_{3k}-S_{2k} Sk,S2k−Sk,S3k−S2k 均不为 0 0 0,则 S k , S 2 k − S k , S 3 k − S 2 k S_k,S_{2k}-S_k,S_{3k}-S_{2k} Sk,S2k−Sk,S3k−S2k 是公比为 q k q^k qk 的等比数列
性质3:若 { a n } \{a_n\} {an} 共有 2 n 2n 2n 项,则 S 偶 S 奇 = q \frac{S_偶}{S_奇}=q S奇S偶=q,若 { a n } \{a_n\} {an} 共有 2 n + 1 2n+1 2n+1 项,则 S 奇 − a 1 S 偶 = q \frac{S_奇-a_1}{S_偶}=q S偶S奇−a1=q
数列中必须重视分类讨论思想
涉及已知 S n S_n Sn 求 a n a_n an 时对 n = 1 n=1 n=1 以及 n ≥ 2 n\ge 2 n≥2 的讨论,求等比数列前 n n n 项和时对 q = 1 q=1 q=1 与 q ≠ 1 q≠1 q=1 的讨论
由数列递推公式求通项公式的常用方法
类型一:累加法 a n + 1 − a n = f ( n ) a_{n+1}-a_n=f(n) an+1−an=f(n)
即利用 a n = a 1 + ( a 2 − a 1 ) + ( a 3 − a 2 ) + . . . + ( a n − a n − 1 ) a_n=a_1+(a_2-a_1)+(a_3-a_2)+...+(a_n-a_{n-1}) an=a1+(a2−a1)+(a3−a2)+...+(an−an−1) 求解
例1:已知 { a n } \{a_n\} {an} 中, a 1 = 1 2 , a n + 1 = a n + 1 4 n 2 − 1 a_1=\frac{1}{2},a_{n+1}=a_n+\frac{1}{4n^2-1} a1=21,an+1=an+4n2−11 求 a n a_n an 通项公式
类型二:累乘法 a n + 1 = a n ⋅ f ( n ) a_{n+1}=a_n·f(n) an+1=an⋅f(n)
即利用 a n = a 1 ⋅ a 2 a 1 ⋅ a 3 a 2 ⋅ ⋅ ⋅ ⋅ ⋅ a n a n − 1 a_n=a_1·\frac{a_2}{a_1}·\frac{a_3}{a_2}·····\frac{a_n}{a_{n-1}} an=a1⋅a1a2⋅a2a3⋅⋅⋅⋅⋅an−1an 求解
例2:已知 { a n } \{a_n\} {an} 中, a 1 = 1 , a n = n ( a n + 1 − a n ) a_1=1,a_{n}=n(a_{n+1}-a_n) a1=1,an=n(an+1−an) 求 a n a_n an
类型三:待定系数法 a n + 1 = c a n + d a_{n+1}=ca_n+d an+1=can+d
1)若 c = 1 c=1 c=1 则为等差数列,略
2)若 d = 0 d=0 d=0 则为等比数列,略
3)若 c ≠ 1 , d ≠ 0 c≠1,d≠0 c=1,d=0,则 { a n } \{a_n\} {an} 为线性递推数列,可以通过待定系数法构造辅助数列
方法演示:设 a n + 1 + λ = c ( a n + λ ) a_{n+1}+\lambda =c(a_n+\lambda) an+1+λ=c(an+λ),得 a n + 1 = c a n + ( c − 1 ) λ a_{n+1} =ca_n+(c-1)\lambda an+1=can+(c−1)λ
与 a n + 1 = c a n + d a_{n+1}=ca_n+d an+1=can+d 比较系数得 ( c − 1 ) λ = d (c-1)\lambda=d (c−1)λ=d,即 λ = d c − 1 \lambda=\frac{d}{c-1} λ=c−1d,所以有 a n + 1 + d c − 1 = c ( a n + d c − 1 ) a_{n+1}+\frac{d}{c-1} =c(a_n+\frac{d}{c-1}) an+1+c−1d=c(an+c−1d)
定义新数列 b n = a n + d c − 1 b_n=a_n+\frac{d}{c-1} bn=an+c−1d,则 b n b_n bn 是公比为 c c c 的等比数列,可以求出通项公式,最后反解出 a n a_n an 通项
例3:已知数列 { a n } \{a_n\} {an} 中, a n = 1 , a n + 1 = 3 a n + 2 a_n=1,a_{n+1}=3a_n+2 an=1,an+1=3an+2,求 { a n } \{a_n\} {an} 通项公式
类型四:取对数法 a n + 1 = p a n r , p > 0 , a n > 0 a_{n+1}=pa_n^r,p>0,a_n>0 an+1=panr,p>0,an>0
例4:设正向数列 { a n } \{a_n\} {an} 满足 a 1 = 1 , a n = 2 a n − 1 2 a_1=1,a_n=2a_{n-1}^2 a1=1,an=2an−12 求通项公式
类型五: a n + 1 = p a n + q n a_{n+1}=pa_n+q^n an+1=pan+qn
法1)原递推公式两边同除 q n + 1 q^{n+1} qn+1 得 a n + 1 q n + 1 = p q ⋅ a n q n + 1 q \frac{a_{n+1}}{q_{n+1}}=\frac{p}{q}·\frac{a_n}{q_n}+\frac{1}{q} qn+1an+1=qp⋅qnan+q1,引入辅助数列 b n = a n q n b_n=\frac{a_n}{q_n} bn=qnan 转化成待定系数法型数列
法2)原递推公式两边同除 p n + 1 p^{n+1} pn+1 得 a n + 1 p n + 1 = a n p n + 1 p ( q p ) n \frac{a_{n+1}}{p_{n+1}}=\frac{a_n}{p_n}+\frac{1}{p}\big(\frac{q}{p}\big)^n pn+1an+1=pnan+p1(pq)n,引入辅助数列 b n = a n p n b_n=\frac{a_n}{p_n} bn=pnan 利用累加法求解
例5:已知数列 a 1 = 5 6 , a n + 1 = 1 3 a n + ( 1 2 ) n + 1 a_1=\frac{5}{6},a_{n+1}=\frac{1}{3}a_n+\big(\frac{1}{2}\big)^{n+1} a1=65,an+1=31an+(21)n+1,求通项公式【用两种方法都做一遍】
类型六:倒数变换法 a n + 1 = a n k a n + b a_{n+1}=\frac{a_n}{ka_n+b} an+1=kan+ban
例6:已知函数 f ( x ) = x x + 1 f(x)=\frac{x}{x+1} f(x)=x+1x ,设数列满足 a n + 1 = f ( a n ) , a 1 = 1 2 a_{n+1}=f(a_n),a_1=\frac{1}{2} an+1=f(an),a1=21 求数列通项公式
数列求和的常用方法
法一:公式法
1)直接用等差、等比数列的求和公式
2)掌握一些常见的数列的前 n n n 项和公式
1 2 + 2 2 + . . . + n 2 = n ( n + 1 ) ( 2 n + 1 ) 6 1^2+2^2+...+n^2=\frac{n(n+1)(2n+1)}{6} 12+22+...+n2=6n(n+1)(2n+1)
例7:数列 { a n } \{a_n\} {an} 是等比数列,若 a 2 = 2 , a 5 = 1 4 a_2=2,a_5=\frac{1}{4} a2=2,a5=41 则 a 1 a 2 + a 2 a 3 + . . . + a n a n + 1 = a_1a_2+a_2a_3+...+a_na_{n+1}= a1a2+a2a3+...+anan+1= _________________________________________________
法二:倒序相加法
如果一个数列 { a n } \{a_n\} {an} 中,与首、末两项 “等距离” 的两项的和相等,那么求这个数列的前 n n n 项和可用倒序相加法,等差数列前 n n n 项和就是这么推导出来的
例8:已知函数 f ( x ) = ( x + 1 ) − 1 f(x)=(x+1)^{-1} f(x)=(x+1)−1,数列 { a n } \{a_n\} {an} 是正项等比数列,且 a 1011 = 1 a_{1011}=1 a1011=1 则 f ( a 1 ) + f ( a 2 ) + . . . + f ( a 2020 ) + f ( a 2021 ) = f(a_1)+f(a_2)+...+f(a_{2020})+f(a_{2021})= f(a1)+f(a2)+...+f(a2020)+f(a2021)=___________________________________________________________
法三:错位相减法
错位相减法求和适用于 { a n ⋅ b n } \{a_n·b_n\} {an⋅bn} 型数列,其中两个数列分别是等差数列和等比数列
例9:已知在等差数列 a n a_n an 中, a 3 = 4 , a 7 = 8 a_3=4,a_7=8 a3=4,a7=8
(1)求 a n a_n an 通项公式
(2)令 b n = a n 2 n − 1 b_n=\frac{a_n}{2^{n-1}} bn=2n−1an,求 b n b_n bn 的前 n n n 项和 T n T_n Tn
法四:裂项相消法
常见的拆项公式有:
1)若 a n a_n an 等差,则 1 a n a n + 1 = 1 d ( 1 a n − 1 a n + 1 ) , 1 a n a n + 2 = 1 2 d ( 1 a n − 1 a n + 2 ) \frac{1}{a_na_{n+1}}=\frac{1}{d}(\frac{1}{a_n}-\frac{1}{a_{n+1}}),\frac{1}{a_na_{n+2}}=\frac{1}{2d}(\frac{1}{a_n}-\frac{1}{a_{n+2}}) anan+11=d1(an1−an+11),anan+21=2d1(an1−an+21)
2) 1 n ( n + 1 ) = 1 n − 1 n + 1 \frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1} n(n+1)1=n1−n+11
3) 1 n ( n + k ) = 1 k ( 1 n − 1 n + k ) \frac{1}{n(n+k)}=\frac{1}{k}(\frac{1}{n}-\frac{1}{n+k}) n(n+k)1=k1(n1−n+k1)
4) 1 ( 2 n − 1 ) ( 2 n + 1 ) = 1 2 ( 1 2 n − 1 − 1 2 n + 1 ) \frac{1}{(2n-1)(2n+1)}=\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1}) (2n−1)(2n+1)1=21(2n−11−2n+11)
5) 1 n ( n + 1 ) ( n + 2 ) = 1 2 [ 1 n ( n + 1 ) − 1 ( n + 1 ) ( n + 2 ) ] \frac{1}{n(n+1)(n+2)}=\frac{1}{2}\Big[\frac{1}{n(n+1)}-\frac{1}{(n+1)(n+2)}\Big] n(n+1)(n+2)1=21[n(n+1)1−(n+1)(n+2)1]
6) 1 n + n + 1 = n + 1 − n \frac{1}{\sqrt n+\sqrt {n+1}}=\sqrt{n+1}-\sqrt n n+n+11=n+1−n
7) 1 n + n + k = 1 k n + k − n \frac{1}{\sqrt n+\sqrt {n+k}}=\frac{1}{k}\sqrt{n+k}-\sqrt n n+n+k1=k1n+k−n
8) 2 n ( 2 n − 1 ) ( 2 n + 1 − 1 ) = 1 2 n − 1 − 1 2 n + 1 − 1 \frac{2^n}{(2^n-1)(2^{n+1}-1)}=\frac{1}{2^n-1}-\frac{1}{2^{n+1}-1} (2n−1)(2n+1−1)2n=2n−11−2n+1−11
9) n + 2 n ( n + 1 ) ⋅ 2 n = 1 2 n − 1 ⋅ n − 1 2 n ⋅ ( n + 1 ) \frac{n+2}{n(n+1)·2^n}=\frac{1}{2^{n-1}·n}-\frac{1}{2^n·(n+1)} n(n+1)⋅2nn+2=2n−1⋅n1−2n⋅(n+1)1
例10:已知数列 a n a_n an 的前 n n n 项和 S n S_n Sn, a 1 = 1 a_1=1 a1=1,对任意的 n ∈ N ∗ n\in N^* n∈N∗ 都有 a n > 0 a_n>0 an>0,且 a n + 1 2 = 2 S n + a n + 1 a_{n+1}^2=2S_n+a_{n+1} an+12=2Sn+an+1
(1)求通项公式
(2)设数列 { 1 a n a n + 2 } \{\frac{1}{a_na_{n+2}}\} {anan+21} 的前 n n n 项和为 T n T_n Tn,求 T n T_n Tn
法五:分组求和法
1)若 a n = b n ± c n a_n=b_n±c_n an=bn±cn 且 b n , c n b_n,c_n bn,cn 为等差或等比数列,可采用分组求和法求 a n a_n an 前 n n n 项和
2)通项公式为 $a_n=\begin{cases} b_n,n为奇数\c_n,n为偶数\end{cases} $ 且 b n , c n b_n,c_n bn,cn 为等差或等比数列,可采用分组求和法求 a n a_n an 前 n n n 项和
例11: a n a_n an 前 n n n 项和为 S n S_n Sn, a 1 = 1 , a n + 1 = 2 a n + 1 a_1=1,a_{n+1}=2a_n+1 a1=1,an+1=2an+1,求证 { a n + 1 } \{a_n+1\} {an+1} 是等比数列且求 S n S_n Sn
法六:并项求和法
1)形如 a n = ( − 1 ) n f ( n ) a_n=(-1)^nf(n) an=(−1)nf(n)
2)周期数列或者具有周期性规律的数列
例12:设各项均为正数的数列 a n a_n an 的前 n n n 项和为 S n S_n Sn,满足 a 1 = 1 , a n 2 = S n + S n − 1 a_1=1,a_n^2=S_n+S_{n-1} a1=1,an2=Sn+Sn−1
(1)证明:数列 { a n } \{a_n\} {an} 为等差数列
(2)若 b n = ( − 1 ) n ( 2 a n ) 2 b_n=(-1)^n(2a_n)^2 bn=(−1)n(2an)2 求数列 b n b_n bn 的前 n n n 项和 T n T_n Tn
用放缩法处理数列和不等问题
先求和再放缩(先裂项求和,再放缩)
例13:正数数列 { a n } \{a_n\} {an} 的前 n n n 项和为 S n , 2 S n = a n + 1 S_n,2\sqrt {S_n}=a_n+1 Sn,2Sn=an+1
(1)求数列通项公式
(2)设 b n = 1 a n a n + 1 b_n=\frac{1}{a_na_{n+1}} bn=anan+11, b n b_n bn 的前 n n n 项和为 B n B_n Bn,求证 B n < 1 2 B_n<\frac{1}{2} Bn<21
例14:设数列 { a n } \{a_n\} {an} 的前 n n n 项和 S n = 4 3 a n − 1 3 2 n + 1 + 2 3 S_n=\frac{4}{3}a_n-\frac{1}{3}2^{n+1}+\frac{2}{3} Sn=34an−312n+1+32
(1)求 a 1 a_1 a1 和通项 a n a_n an
(2)设 T n = 2 n S n T_n=\frac{2^n}{S_n} Tn=Sn2n,证明 ∑ i = 1 n T i < 3 2 \sum_{i=1}^n T_i<\frac{3}{2} ∑i=1nTi<23
先放缩再求和
放缩成等比数列,再求和
例15:等比数列 { a n } \{a_n\} {an} 中, a 1 = − 1 2 a_1=-\frac{1}{2} a1=−21,前 n n n 项和为 S n S_n Sn,且 S 7 , S 9 , S 8 S_7,S_9,S_8 S7,S9,S8 成等差数列
设 b n = a n 2 1 − a n b_n=\frac{a_n^2}{1-a_n} bn=1−anan2,数列 { b n } \{b_n\} {bn} 的前 n n n 项和为 T n T_n Tn ,求证 T n < 1 3 T_n<\frac 13 Tn<31
例16:已知数列满足 a 1 = 1 , a n + 1 = 2 a n + 1 a_1=1,a_{n+1}=2a_n+1 a1=1,an+1=2an+1
(1)求通项公式
(2)若数列 b n b_n bn 满足 4 b 1 − 1 4 b 2 − 1 . . . . 4 b n − 1 = ( a n + 1 ) b n 4^{b_1-1}4^{b_2-1}....4^{b_n-1}=(a_n+1)^{b_n} 4b1−14b2−1....4bn−1=(an+1)bn 求证 { b n } \{b_n\} {bn} 是等差数列
(3)证明 n 2 − 1 3 < a 1 a 2 + a 2 a 3 + . . . + a n a n + 1 < n 2 \frac{n}{2}-\frac{1}{3}<\frac{a_1}{a_2}+\frac{a_2}{a_3}+...+\frac{a_n}{a_{n+1}}<\frac n2 2n−31<a2a1+a3a2+...+an+1an<2n
放缩为差比数列,再求和
例17:已知数列 { a n } \{a_n\} {an} 满足 a 1 = 1 , a n + 1 = ( 1 + n 2 n ) a n a_1=1,a_{n+1}=(1+\frac{n}{2^n})a_n a1=1,an+1=(1+2nn)an 求证 a n + 1 > a n ≥ 3 − n + 1 2 n − 1 a_{n+1}>a_n\ge 3-\frac{n+1}{2^{n-1}} an+1>an≥3−2n−1n+1
放缩为等差数列,再求和
例18:已知各项均为正数的数列 { a n } \{a_n\} {an} 前 n n n 项和为 S n S_n Sn,且 a n 2 + a n = 2 S n a_n^2+a_n=2S_n an2+an=2Sn
(1)求证 S n < a n 2 + a n + 1 2 4 S_n<\frac{a_n^2+a_{n+1}^2}{4} Sn<4an2+an+12
(2)求证 S n 2 < S 1 + S 2 + . . . + S n < S n + 1 − 1 2 \frac{S_n}{\sqrt 2}<\sqrt {S_1}+\sqrt{S_2}+...+\sqrt{S_n}<\frac{S_{n+1}-1}{\sqrt 2} 2Sn<S1+S2+...+Sn<2Sn+1−1
函数放缩(构造函数,通过单调性放缩)
相关文章:

【高中数学】数列
等差数列前 n n n 项和性质 公式一: S n n ( a 1 a n ) 2 S_n\frac{n(a_1a_n)}{2} Sn2n(a1an) 公式二: S n n a 1 n ( n − 1 ) 2 d S_nna_1\frac{n(n-1)}{2}d Snna12n(n−1)d 性质1:等差数列中依次 k k k 项之和 S …...

数字媒体技术基础:AMF(ACES 元数据文件 )
在现代电影和电视制作中,色彩管理变得越来越重要。ACES(Academy Color Encoding System,美国电影艺术与科学学院颜色编码系统)是一个广泛采用的色彩管理和交换系统,旨在解决不同设备、软件和工作流程之间的色彩不一致问…...

Apache Dubbo (RPC框架)
本文参考官方文档:Apache Dubbo 1. Dubbo 简介与核心功能 Apache Dubbo 是一个高性能、轻量级的开源Java RPC框架,用于快速开发高性能的服务。它提供了服务的注册、发现、调用、监控等核心功能,以及负载均衡、流量控制、服务降级等高级功能。…...
LeetCode 3226. 使两个整数相等的位更改次数
. - 力扣(LeetCode) 题目 给你两个正整数 n 和 k。你可以选择 n 的 二进制表示 中任意一个值为 1 的位,并将其改为 0。 返回使得 n 等于 k 所需要的更改次数。如果无法实现,返回 -1。 示例 1: 输入: n …...

面试经典 150 题:189、383
189. 轮转数组 【参考代码】 class Solution { public:void rotate(vector<int>& nums, int k) {int size nums.size();if(1 size){return;}vector<int> temp(size);//k k % size;for(int i0; i<size; i){temp[(i k) % size] nums[i];}nums temp; }…...

Python模拟真人动态生成鼠标滑动路径
一.简介 鼠标轨迹算法是一种模拟人类鼠标操作的程序,它能够模拟出自然而真实的鼠标移动路径。 鼠标轨迹算法的底层实现采用C/C语言,原因在于C/C提供了高性能的执行能力和直接访问操作系统底层资源的能力。 鼠标轨迹算法具有以下优势: 模拟…...
如何压缩pdf文件的大小?5分钟压缩pdf的方法推荐
如何压缩pdf文件的大小?在现代办公和学习中,PDF文件因其稳定性和广泛的兼容性被广泛使用。然而,随着文件内容的增多,制作好的PDF文件常常变得过大,给使用带来了诸多不便。无论是电子邮件附件的发送,还是在线…...

【SQL】[2BP01] ERROR: cannot drop table course because other objects depend on it
问题描述 在尝试执行以下SQL语句时,发生错误。 DROP TABLE Course RESTRICT;执行以上语句后,系统返回了一个错误提示: [2BP01] ERROR: cannot drop table course because other objects depend on it 详细:constraint sc_cno_…...

gbase8s之spring框架用druid中间件报语法错误
spring框架 调用druid中间件 时报这个错: MetaDataAccessException: Could not get Connection for extracting meta-data; nested exception is org.springframework.jdbc.CannotGetJdbcConnectionException: Failed to obtain JDBC Connection; nested exception …...
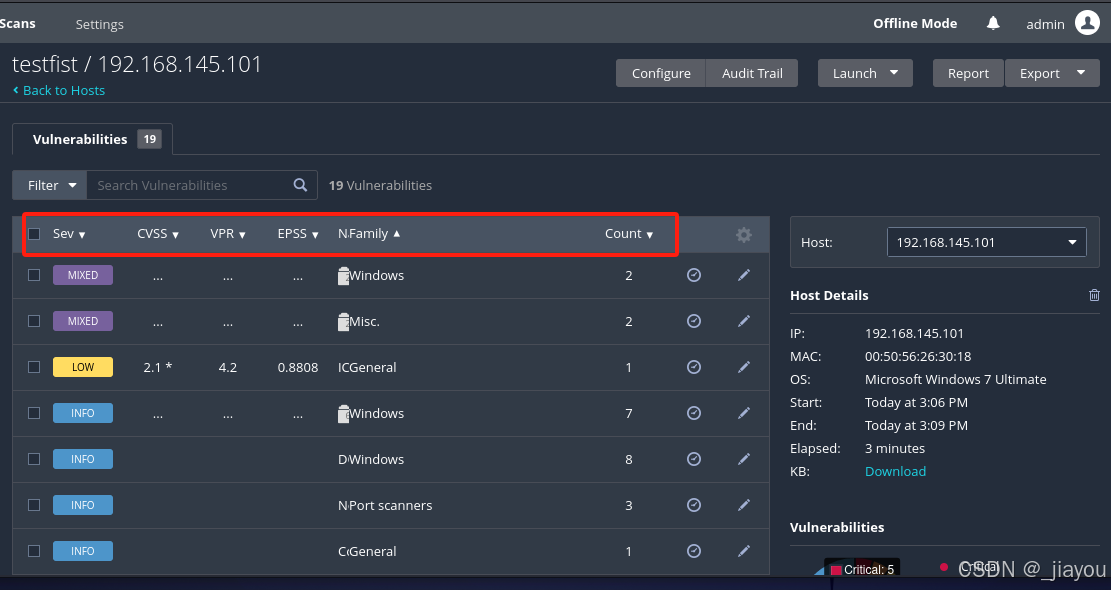
【网络安全】|nessus使用
1、扫描结果分析: Sev:漏洞的严重性级别 CVSS:量化漏洞严重性的标准,通过计算得出一个分数,分数越高表示漏洞越严重。 VPR:基于风险的评分系统,帮助组织优先处理风险最高的漏洞。 EPSS…...

CSRA2的LINUX操作系统24年11月2日上午上课笔记
几个查找命令: .whereis:查看文件的路径,查看可执行文件的路径,一级相应文档路径。 .which:查看系统可执行的文件的路径,以及命令的别名等信息 .local:他会将linux中的所有文件的路径信息保存到数据库中,在数据库中查…...
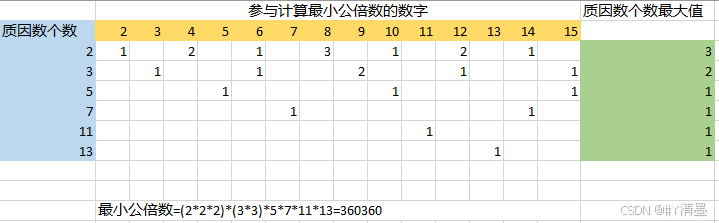
通过分解质因数求若干个数的最小公倍数
求最小公倍数的常规方法回顾 暴力枚举法 long long work(long long a,long long b) {for(long long imax(a,b);;i)if(i%a0&&i%b0)return i; }大数翻倍法 long long work(long long a,long long b) {if(a<b) swap(a,b);for(long long ia;;ia) // i 是 a 的倍数&#…...
数据库三范式(1NF、2NF、3NF)
1NF(第一范式) 定义:确保每一列都是原子值,即是不可分割的基础数据项。 所谓第一范式(1NF)是指在关系模型中,对于添加列的一个规范要求,所有的列都 应该是原子性的,即数…...

C语言_数据结构_顺序表
1. 本章重点 顺序表初始化顺序表尾插顺序表尾删顺序表头插顺序表头删顺序表查找顺序表在pos位置插入x顺序表删除pos位置的值顺序表销毁顺序表打印 2. 顺序表的概念及结构 顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构,一般情况下采用数组存储…...
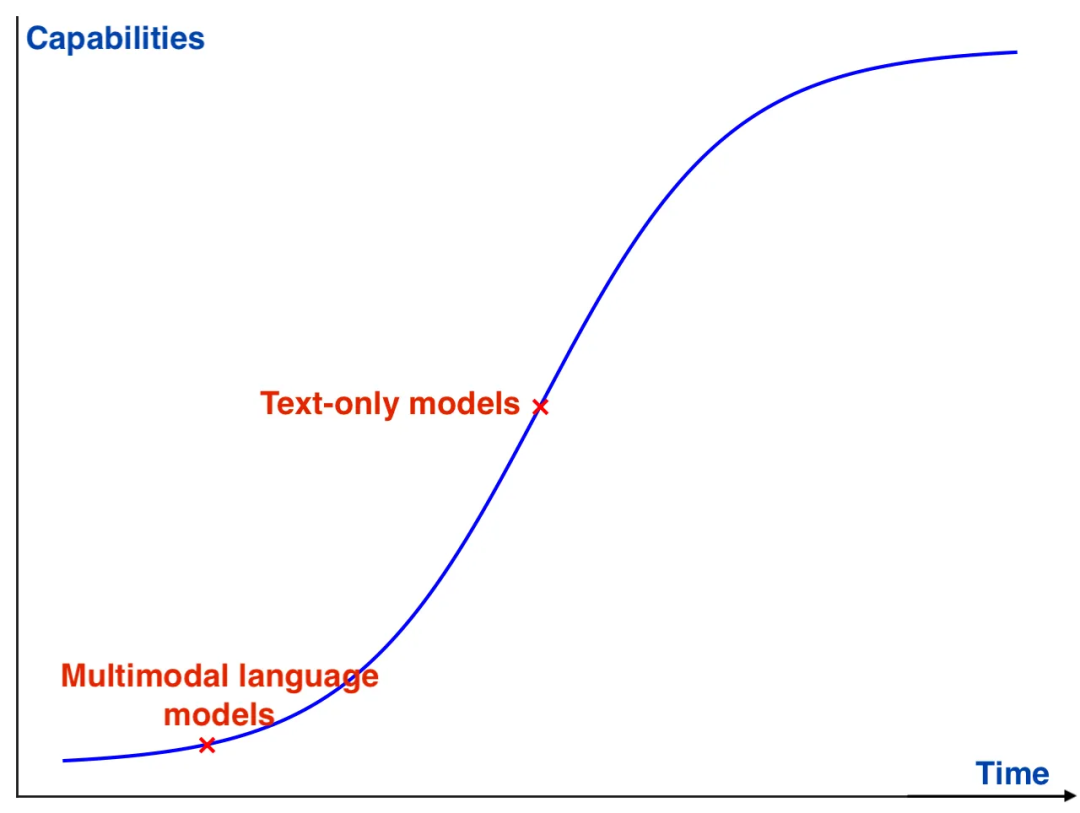
Llama 3.2 Vision Molmo:多模态开源生态系统基础
编者按: 视觉功能的融入对模型能力和推理方式的影响如何?当我们需要一个既能看懂图像、又能生成文本的 AI 助手时,是否只能依赖于 GPT-4V 这样的闭源解决方案? 我们今天为大家分享的这篇文章,作者的核心观点是…...

【数据结构与算法】第6课—数据结构之栈
文章目录 1. 栈2. 栈的初始化和栈的销毁3. 入栈和出栈(压栈)4. 取栈顶元素并打印5. 栈的练习题5.1 有效的括号 1. 栈 栈:也是一种线性表,其数据结构与动态顺序表的数据结构类似栈分为栈顶和栈底,在栈中,插入…...

开源全站第一个Nextron(NextJS+electron)项目--NextTalk:一款集成chatgpt的实时聊天工具
NextTalk 简介 该项目是一个基于Nextron(NextJSElectron)的桌面端实时聊天工具。 但由于使用了NextJS中的ssr及api route功能,该程序只能在开发环境运行。 关于生产版本:我将其网页端部分分离,并用Pake将其打包成桌面端,生产体…...

多样化的编程模型:并发与并行策略
因为经常看着某些框架设计的编程模型很晕,所以自己梳理总结了一下编程模型的分类,总共六个大类,基本所有常见框架设计的编程模型都是基于这六个大类来实现的,如果有错误的地方,请见谅并不吝赐教,感谢&#…...

npm入门教程2:npm历史
一、起源与诞生 时间背景:npm的诞生与Node.js的兴起紧密相关。Node.js是一个基于Chrome V8引擎的JavaScript运行环境,它允许JavaScript代码在服务器端运行。随着Node.js的流行,开发者们对于包管理和依赖解决的需求日益增长。诞生:…...
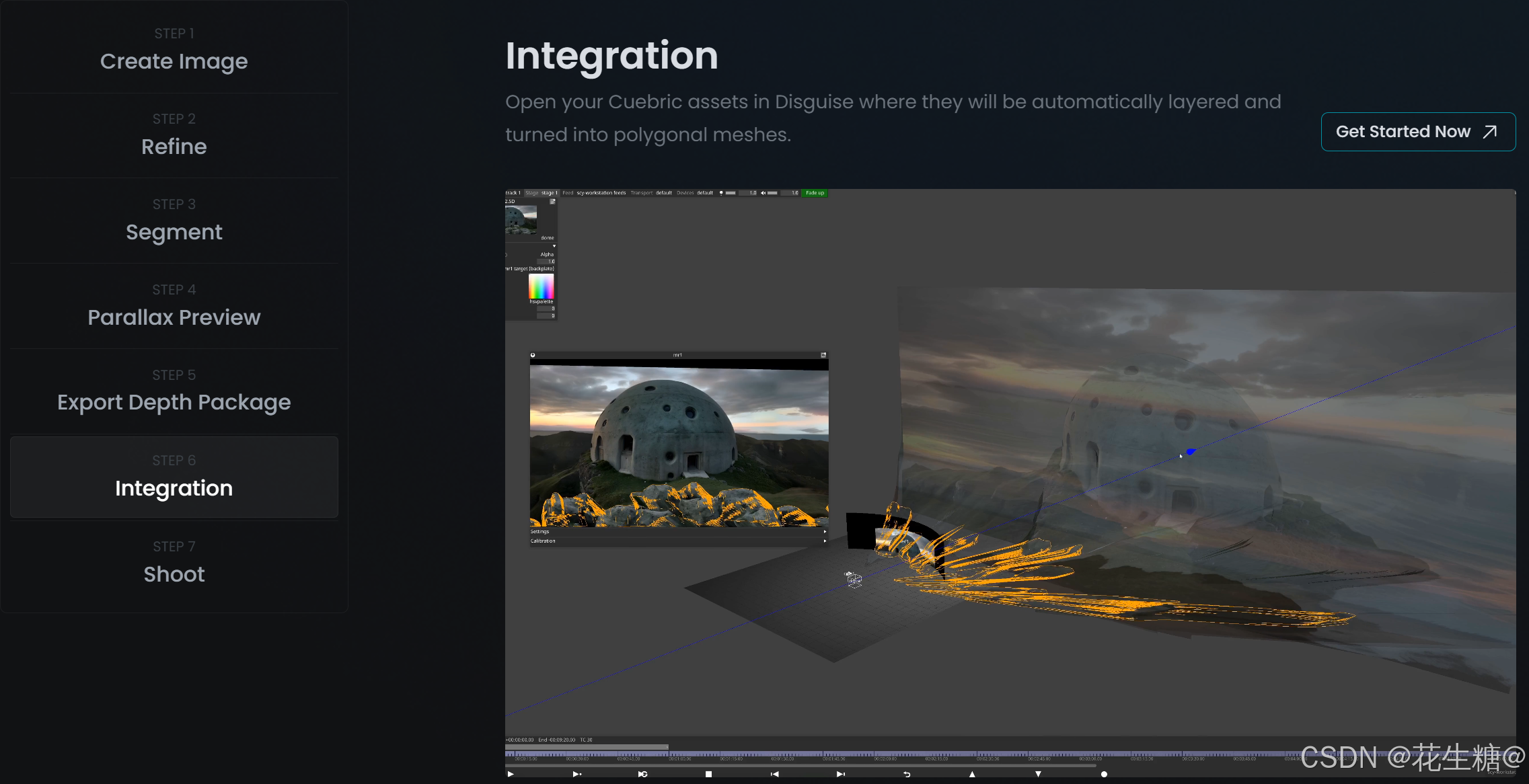
Cuebric:用AI重新定义3D创作的未来
一、简介 Cuebric 是一家成立于2022年夏天的好莱坞创新公司,致力于为电影、电视、游戏和时尚等行业提供先进的AI多模态SaaS平台。自2024年1月正式推出以来,Cuebric 已经在市场上获得了广泛的认可和积极的反馈。目前,该平台正处于1.0版本的beta测试阶段,已募集约50万美元的…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...
