通过分解质因数求若干个数的最小公倍数
求最小公倍数的常规方法回顾
暴力枚举法
long long work(long long a,long long b)
{for(long long i=max(a,b);;i++)if(i%a==0&&i%b==0)return i;
}
大数翻倍法
long long work(long long a,long long b)
{if(a<b) swap(a,b);for(long long i=a;;i+=a) // i 是 a 的倍数,每次增加一倍,i 必然是 a 的倍数,我们只要保证 i 也是 b 的倍数,那么 i 就一定是 a,b 的最小公倍数if(i%b==0)return i;
}
公式法
long long work(long long a,long long b)
{long long c = __gcd(a,b); // 先求 a,b 的最大公约数return a*b/c; //按照公式算出最小公倍数
}
分解质因数求若干个数的最小公倍数
有n个数a[i](i从1到n),求它们的最小公倍数可以采用下面方法:
-
求出 max(a[i]),算出 小于等于 max(a[i]) 的所有质数 bjbj
-
对每一个a[i]进行质因数分解,进而得到 c[i] c[j]其含义为对a[i]分解质因数,能分解出c[i] c[j] 个质因数b[j]。
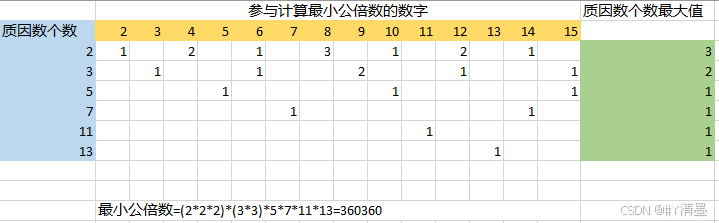
下面,我们举一个例子,假设我们要求 2 到 15 的最小公倍数。
-
2,4,6,8,10,12,14 都能分解出质因数 2 ,最多能分解出 3 个(8 分解出 3 个 2),所以,最少公倍数一定包含 3 个质因数 2 (不可能小于 3 个,否则就不可能是 8 的倍数;也不可能多于 3 个,否则就不是最小的倍数)
-
3,6,9,12,15 都能分解出质因数 3,最多能分解出 2 个 3(9 分解出 2 个 3),所以,最少公倍数一定包含 2 个质因数 3
-
5,10,15 都能分解出质因数 5,均只能分解出 1 个 5,所以,最少公倍数一定包含 1 个质因数 5
.....
通过分解质因数的方法求最小公倍数的应用场景
有一些题目并不需要真正输出最小公倍数的具体数值是什么。只需要根据这个分解情况进行下一步计算,分解法在这个时候特别有意义。
公式法中出现除的运算。意味着,中间答案可能会很大,容易溢出。另外,因为有除法的出现,就导致了同余定理不能使用。用分解法来求质因数,最终结果就是对很多很多个质因数乘起来,乘法和加法都是可以运用同余定理的。
相关文章:

通过分解质因数求若干个数的最小公倍数
求最小公倍数的常规方法回顾 暴力枚举法 long long work(long long a,long long b) {for(long long imax(a,b);;i)if(i%a0&&i%b0)return i; }大数翻倍法 long long work(long long a,long long b) {if(a<b) swap(a,b);for(long long ia;;ia) // i 是 a 的倍数&#…...
数据库三范式(1NF、2NF、3NF)
1NF(第一范式) 定义:确保每一列都是原子值,即是不可分割的基础数据项。 所谓第一范式(1NF)是指在关系模型中,对于添加列的一个规范要求,所有的列都 应该是原子性的,即数…...

C语言_数据结构_顺序表
1. 本章重点 顺序表初始化顺序表尾插顺序表尾删顺序表头插顺序表头删顺序表查找顺序表在pos位置插入x顺序表删除pos位置的值顺序表销毁顺序表打印 2. 顺序表的概念及结构 顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构,一般情况下采用数组存储…...
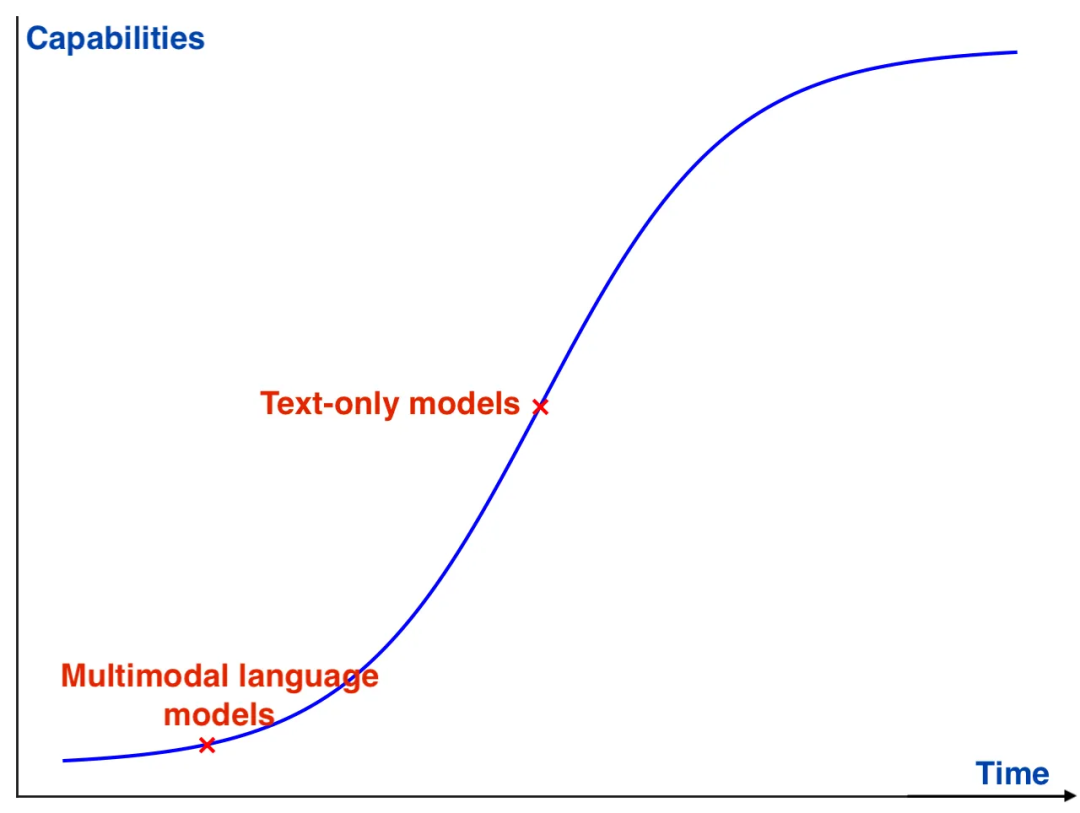
Llama 3.2 Vision Molmo:多模态开源生态系统基础
编者按: 视觉功能的融入对模型能力和推理方式的影响如何?当我们需要一个既能看懂图像、又能生成文本的 AI 助手时,是否只能依赖于 GPT-4V 这样的闭源解决方案? 我们今天为大家分享的这篇文章,作者的核心观点是…...

【数据结构与算法】第6课—数据结构之栈
文章目录 1. 栈2. 栈的初始化和栈的销毁3. 入栈和出栈(压栈)4. 取栈顶元素并打印5. 栈的练习题5.1 有效的括号 1. 栈 栈:也是一种线性表,其数据结构与动态顺序表的数据结构类似栈分为栈顶和栈底,在栈中,插入…...

开源全站第一个Nextron(NextJS+electron)项目--NextTalk:一款集成chatgpt的实时聊天工具
NextTalk 简介 该项目是一个基于Nextron(NextJSElectron)的桌面端实时聊天工具。 但由于使用了NextJS中的ssr及api route功能,该程序只能在开发环境运行。 关于生产版本:我将其网页端部分分离,并用Pake将其打包成桌面端,生产体…...

多样化的编程模型:并发与并行策略
因为经常看着某些框架设计的编程模型很晕,所以自己梳理总结了一下编程模型的分类,总共六个大类,基本所有常见框架设计的编程模型都是基于这六个大类来实现的,如果有错误的地方,请见谅并不吝赐教,感谢&#…...

npm入门教程2:npm历史
一、起源与诞生 时间背景:npm的诞生与Node.js的兴起紧密相关。Node.js是一个基于Chrome V8引擎的JavaScript运行环境,它允许JavaScript代码在服务器端运行。随着Node.js的流行,开发者们对于包管理和依赖解决的需求日益增长。诞生:…...
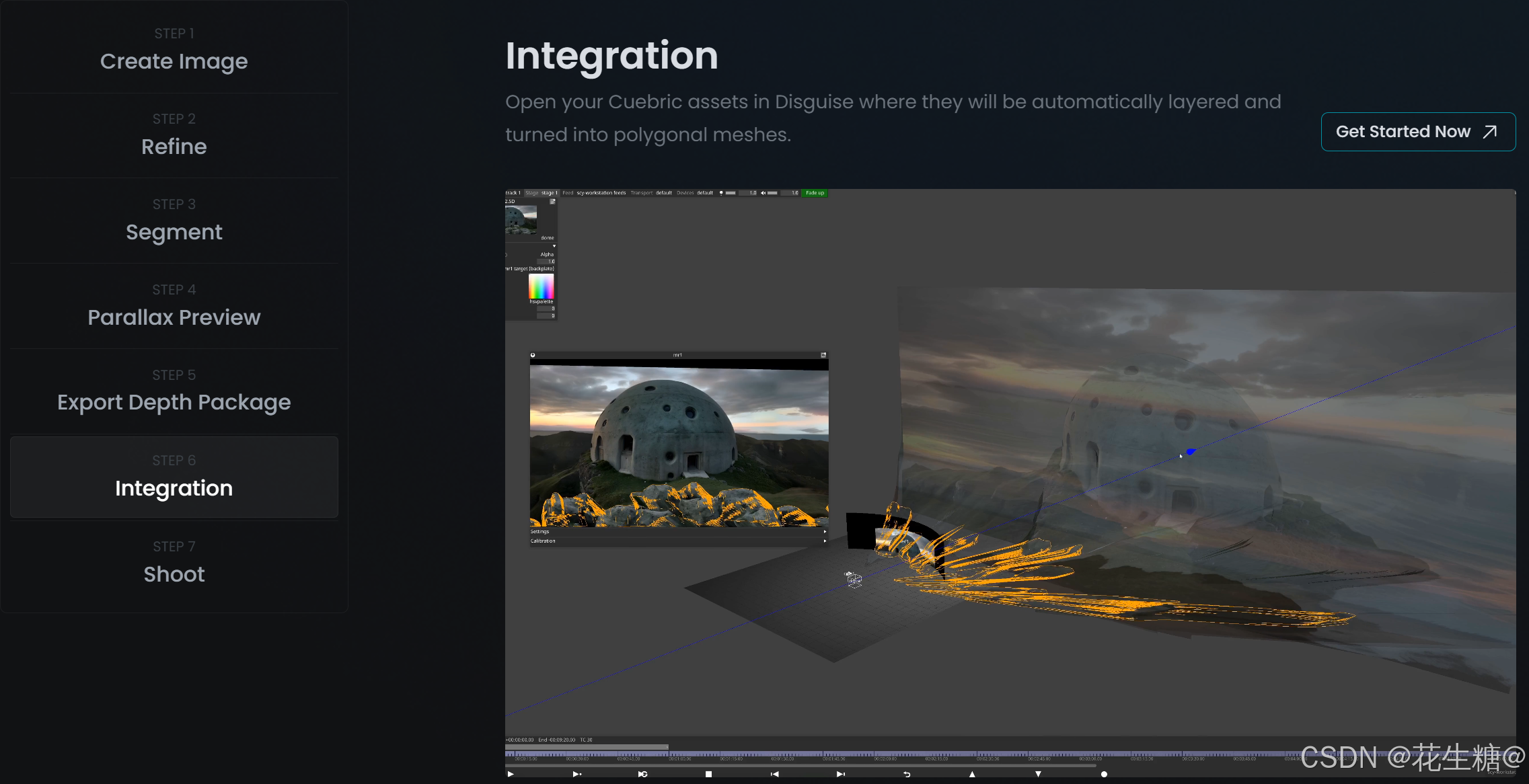
Cuebric:用AI重新定义3D创作的未来
一、简介 Cuebric 是一家成立于2022年夏天的好莱坞创新公司,致力于为电影、电视、游戏和时尚等行业提供先进的AI多模态SaaS平台。自2024年1月正式推出以来,Cuebric 已经在市场上获得了广泛的认可和积极的反馈。目前,该平台正处于1.0版本的beta测试阶段,已募集约50万美元的…...
)
前端react常见面试题目(basic)
1. 如果 React 组件的属性没有传值,它的默认值是什么? 如果一个 React 组件的属性(props)没有传值,那么它的默认值会是 undefined。你可以通过组件内部的逻辑来设置默认值,比如使用逻辑运算符或者 ES6 的默认参数。 …...

机器人技术基础(4章逆运动解算和雅克比矩阵)
逆运动解算: 雅克比矩阵: 将动力学分析转向运动的物体 下图中的 n o y 反映了机器人的姿态矩阵, 最后一列 p 反应了机器人在空间中的位置:...
OpenGL入门002——顶点着色器和片段着色器
文章目录 一些概念坐标转换阶段顶点着色器片段着色器VBOVAO 实战简介main.cppCMakeLists.txt最终效果 一些概念 坐标转换阶段 概述: 模型空间、世界空间、视图空间和裁剪空间是对象在3D场景中经历的不同坐标变换阶段。每个空间对应渲染管道的一个步骤,…...

[数组排序] LCR 164. 破解闯关密码
文章目录 1. 题目链接2. 题目大意3. 示例4. 解题思路5. 参考代码 1. 题目链接 LCR 164. 破解闯关密码 - 力扣(LeetCode) 2. 题目大意 描述:给定一个非负整数数组 nums。 要求:将数组中的数字拼接起来排成一个数,打印…...
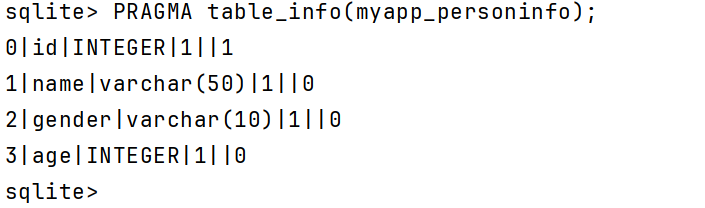
05 Django 框架模型介绍(一)
文章目录 1、Django 模型简介2、Django 中创建并使用模型(1)新加一个名为 myapp 的应用(2)定义模型类(2)激活模型类(3)创建数据库迁移文件(4)应用迁移文件 3、…...
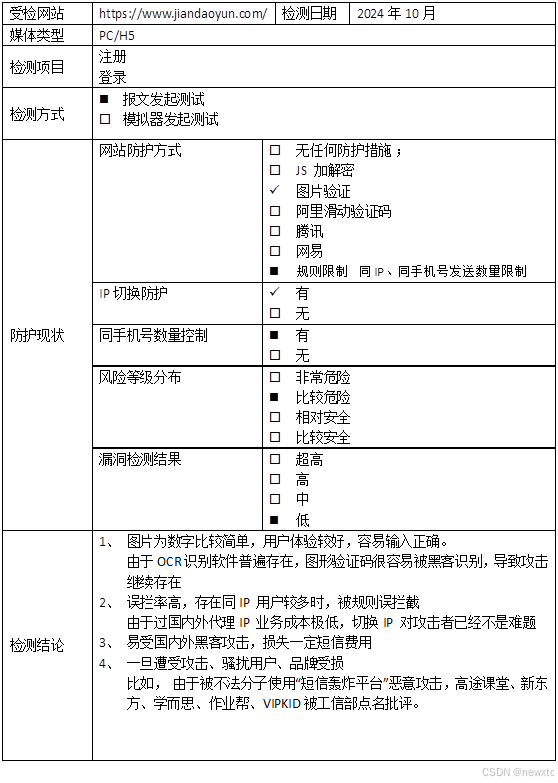
【简道云 -注册/登录安全分析报告】
前言 由于网站注册入口容易被黑客攻击,存在如下安全问题: 暴力破解密码,造成用户信息泄露短信盗刷的安全问题,影响业务及导致用户投诉带来经济损失,尤其是后付费客户,风险巨大,造成亏损无底洞…...

【C++题解】1970. 判断是什么字符
欢迎关注本专栏《C从零基础到信奥赛入门级(CSP-J)》 问题:1970. 判断是什么字符 类型:字符串、字符型 题目描述: 从键盘读入一个字符,有可能是大写字母、小写字母、数字中的一种,请编程判断&…...

Python自动化操作Word文档详解
在日常办公和数据处理中,我们经常需要处理Word文档。手动操作Word文档可能会非常繁琐和耗时,而使用Python可以实现自动化操作,提高工作效率。本文将详细介绍如何使用Python自动化操作Word文档,包括读取、写入、修改和格式化等操作…...
-中位值滤波法)
常用滤波算法(二)-中位值滤波法
文章目录 一、中位值滤波法简介二、C语言实现中位值滤波法三、程序说明信号初始化:滤波窗口大小:内存分配:中位值滤波函数:中位值计算函数:内存释放: 四、总结 中位值滤波法,作为一种非线性滤波…...

HCIP--以太网交换安全(总实验)
实验背景 假如你是公司的网络管理员,为了提高公司网络安全性,你决定在接入交换机部署一些安全技术:端口隔、端口安全、DHCP snooping、IPSG。 实验拓扑图 实验的要求: 1.在R1、R2连接在GE0/0/1和GE0/0/2接口下,均划…...

C语言 | Leetcode C语言题解之第519题随机翻转矩阵
题目: 题解: typedef struct {unsigned long long val;UT_hash_handle hh; } Hash;typedef struct {Hash *hash;int n_rows;int n_cols; } Solution, SL;Solution* solutionCreate(int n_rows, int n_cols) {SL *obj malloc(sizeof(SL));obj->hash …...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
