LeetCode 3226. 使两个整数相等的位更改次数
. - 力扣(LeetCode)
题目
给你两个正整数 n 和 k。你可以选择 n 的 二进制表示 中任意一个值为 1 的位,并将其改为 0。
返回使得 n 等于 k 所需要的更改次数。如果无法实现,返回 -1。
- 示例 1:
- 输入: n = 13, k = 4
- 输出: 2
- 解释:最初,
n和k的二进制表示分别为n = (1101)2和k = (0100)2,我们可以改变n的第一位和第四位。结果整数为n = (0100)2 = k。
- 示例 2:
- 输入: n = 21, k = 21
- 输出: 0
- 解释:
n和k已经相等,因此不需要更改。
- 示例 3:
- 输入: n = 14, k = 13
- 输出: -1
- 解释:无法使
n等于k。
解题方案
1. 逐位遍历
依次取n和k最后一位,进行比较
- 如果last_n == last_k, 则不需要修改,继续遍历
- 如果lask_n != last_k:
- 如果last_n == 1, last_k == 0, 则需要改变操作,操作数+1
- 如果last_n == 0, last_k == 1, 则无法通过指定操作使n变成k, 直接返回-1
class Solution:def minChanges(self, n: int, k: int) -> int:if n < k:return -1if n == k:return 0mod = 0while k > 0 or n > 0:last_n = n & 1 # 取n的最后一位last_k = k & 1 # 取k的最后一位n = n >> 1k = k >> 1if last_n == last_k:print(last_n, last_k, n, k, mod)continueelif last_k == 1:return - 1else:mod += 1 print(last_n, last_k, n, k, mod)return mod分析复杂度
-
时间复杂度是n和k位数的最大值:
-
空间复杂度是
2. 位操作
如果把n和k的二进制为1的位分别看做一个集合,那么k应该是n的一个子集。
1. 按位或操作,如果操作结果等于k,则n可以通过修改某些位置上1为0得到k;反之则不能,直接返回-1.
2. 已知n可以通过修改某些位置上1为0得到k,接下来进行异或操作(n和k不同的位为1,即需要修改的位为1),统计操作结果中1的位数即可
class Solution:def minChanges(self, n: int, k: int) -> int:return (n ^ k).bit_count() if (n & k) == k else -1分析复杂度
- 时间复杂度 O(1)
- 空间复杂度 O(1)
相关文章:
LeetCode 3226. 使两个整数相等的位更改次数
. - 力扣(LeetCode) 题目 给你两个正整数 n 和 k。你可以选择 n 的 二进制表示 中任意一个值为 1 的位,并将其改为 0。 返回使得 n 等于 k 所需要的更改次数。如果无法实现,返回 -1。 示例 1: 输入: n …...

面试经典 150 题:189、383
189. 轮转数组 【参考代码】 class Solution { public:void rotate(vector<int>& nums, int k) {int size nums.size();if(1 size){return;}vector<int> temp(size);//k k % size;for(int i0; i<size; i){temp[(i k) % size] nums[i];}nums temp; }…...

Python模拟真人动态生成鼠标滑动路径
一.简介 鼠标轨迹算法是一种模拟人类鼠标操作的程序,它能够模拟出自然而真实的鼠标移动路径。 鼠标轨迹算法的底层实现采用C/C语言,原因在于C/C提供了高性能的执行能力和直接访问操作系统底层资源的能力。 鼠标轨迹算法具有以下优势: 模拟…...
如何压缩pdf文件的大小?5分钟压缩pdf的方法推荐
如何压缩pdf文件的大小?在现代办公和学习中,PDF文件因其稳定性和广泛的兼容性被广泛使用。然而,随着文件内容的增多,制作好的PDF文件常常变得过大,给使用带来了诸多不便。无论是电子邮件附件的发送,还是在线…...

【SQL】[2BP01] ERROR: cannot drop table course because other objects depend on it
问题描述 在尝试执行以下SQL语句时,发生错误。 DROP TABLE Course RESTRICT;执行以上语句后,系统返回了一个错误提示: [2BP01] ERROR: cannot drop table course because other objects depend on it 详细:constraint sc_cno_…...

gbase8s之spring框架用druid中间件报语法错误
spring框架 调用druid中间件 时报这个错: MetaDataAccessException: Could not get Connection for extracting meta-data; nested exception is org.springframework.jdbc.CannotGetJdbcConnectionException: Failed to obtain JDBC Connection; nested exception …...
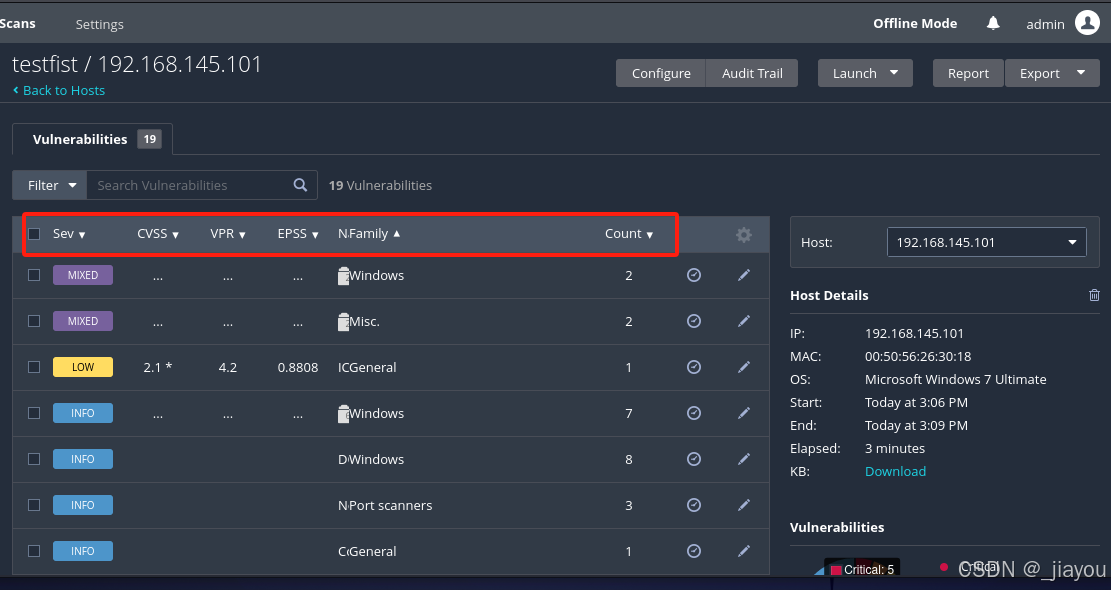
【网络安全】|nessus使用
1、扫描结果分析: Sev:漏洞的严重性级别 CVSS:量化漏洞严重性的标准,通过计算得出一个分数,分数越高表示漏洞越严重。 VPR:基于风险的评分系统,帮助组织优先处理风险最高的漏洞。 EPSS…...

CSRA2的LINUX操作系统24年11月2日上午上课笔记
几个查找命令: .whereis:查看文件的路径,查看可执行文件的路径,一级相应文档路径。 .which:查看系统可执行的文件的路径,以及命令的别名等信息 .local:他会将linux中的所有文件的路径信息保存到数据库中,在数据库中查…...
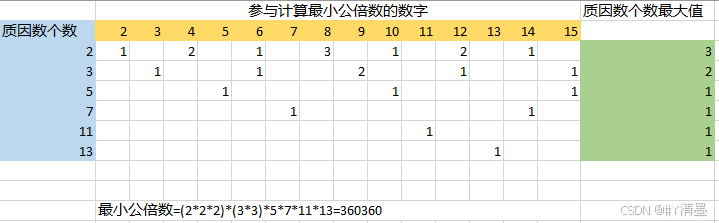
通过分解质因数求若干个数的最小公倍数
求最小公倍数的常规方法回顾 暴力枚举法 long long work(long long a,long long b) {for(long long imax(a,b);;i)if(i%a0&&i%b0)return i; }大数翻倍法 long long work(long long a,long long b) {if(a<b) swap(a,b);for(long long ia;;ia) // i 是 a 的倍数&#…...
数据库三范式(1NF、2NF、3NF)
1NF(第一范式) 定义:确保每一列都是原子值,即是不可分割的基础数据项。 所谓第一范式(1NF)是指在关系模型中,对于添加列的一个规范要求,所有的列都 应该是原子性的,即数…...

C语言_数据结构_顺序表
1. 本章重点 顺序表初始化顺序表尾插顺序表尾删顺序表头插顺序表头删顺序表查找顺序表在pos位置插入x顺序表删除pos位置的值顺序表销毁顺序表打印 2. 顺序表的概念及结构 顺序表是用一段物理地址连续的存储单元依次存储数据元素的线性结构,一般情况下采用数组存储…...
Llama 3.2 Vision Molmo:多模态开源生态系统基础
编者按: 视觉功能的融入对模型能力和推理方式的影响如何?当我们需要一个既能看懂图像、又能生成文本的 AI 助手时,是否只能依赖于 GPT-4V 这样的闭源解决方案? 我们今天为大家分享的这篇文章,作者的核心观点是…...

【数据结构与算法】第6课—数据结构之栈
文章目录 1. 栈2. 栈的初始化和栈的销毁3. 入栈和出栈(压栈)4. 取栈顶元素并打印5. 栈的练习题5.1 有效的括号 1. 栈 栈:也是一种线性表,其数据结构与动态顺序表的数据结构类似栈分为栈顶和栈底,在栈中,插入…...

开源全站第一个Nextron(NextJS+electron)项目--NextTalk:一款集成chatgpt的实时聊天工具
NextTalk 简介 该项目是一个基于Nextron(NextJSElectron)的桌面端实时聊天工具。 但由于使用了NextJS中的ssr及api route功能,该程序只能在开发环境运行。 关于生产版本:我将其网页端部分分离,并用Pake将其打包成桌面端,生产体…...

多样化的编程模型:并发与并行策略
因为经常看着某些框架设计的编程模型很晕,所以自己梳理总结了一下编程模型的分类,总共六个大类,基本所有常见框架设计的编程模型都是基于这六个大类来实现的,如果有错误的地方,请见谅并不吝赐教,感谢&#…...

npm入门教程2:npm历史
一、起源与诞生 时间背景:npm的诞生与Node.js的兴起紧密相关。Node.js是一个基于Chrome V8引擎的JavaScript运行环境,它允许JavaScript代码在服务器端运行。随着Node.js的流行,开发者们对于包管理和依赖解决的需求日益增长。诞生:…...
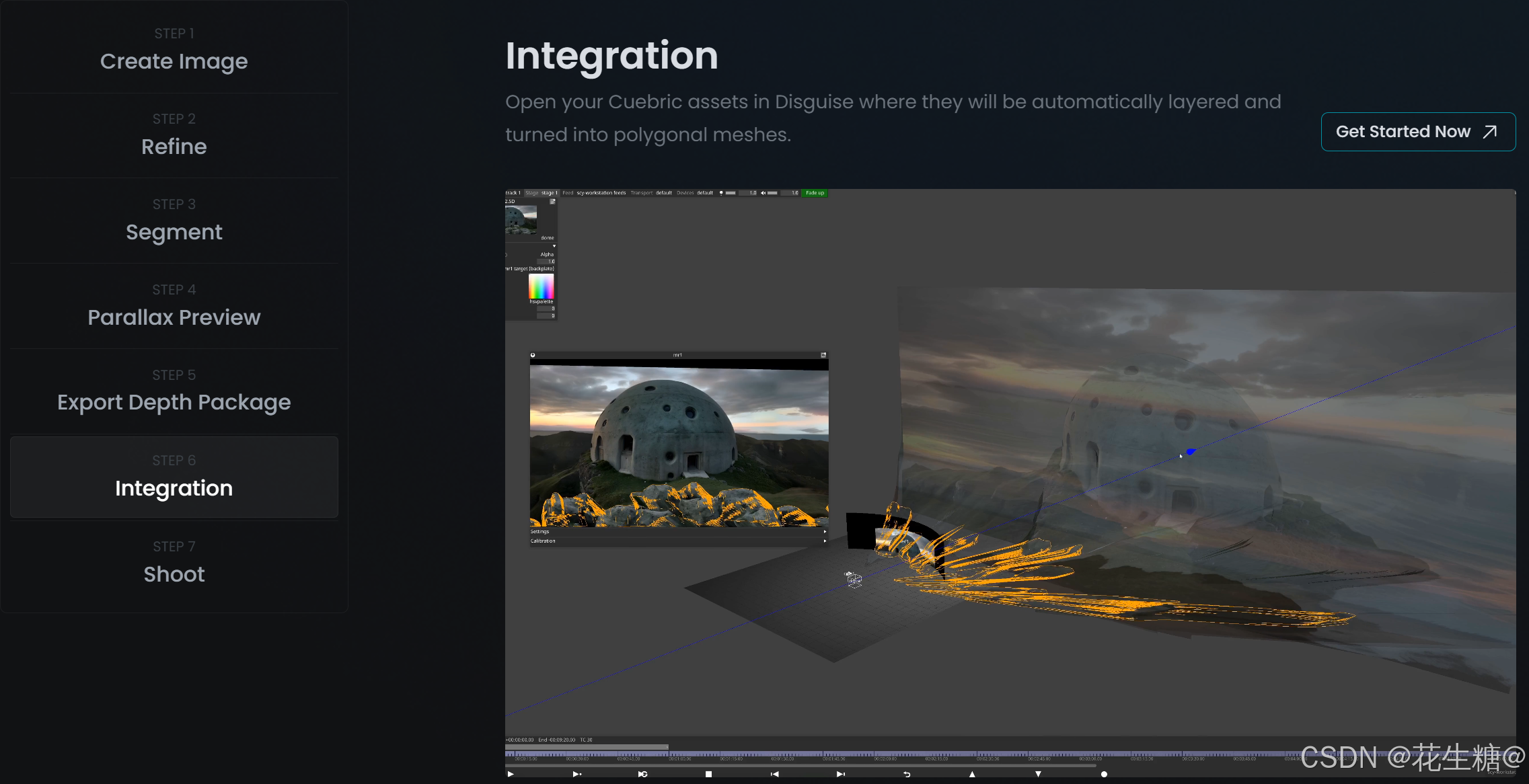
Cuebric:用AI重新定义3D创作的未来
一、简介 Cuebric 是一家成立于2022年夏天的好莱坞创新公司,致力于为电影、电视、游戏和时尚等行业提供先进的AI多模态SaaS平台。自2024年1月正式推出以来,Cuebric 已经在市场上获得了广泛的认可和积极的反馈。目前,该平台正处于1.0版本的beta测试阶段,已募集约50万美元的…...
)
前端react常见面试题目(basic)
1. 如果 React 组件的属性没有传值,它的默认值是什么? 如果一个 React 组件的属性(props)没有传值,那么它的默认值会是 undefined。你可以通过组件内部的逻辑来设置默认值,比如使用逻辑运算符或者 ES6 的默认参数。 …...

机器人技术基础(4章逆运动解算和雅克比矩阵)
逆运动解算: 雅克比矩阵: 将动力学分析转向运动的物体 下图中的 n o y 反映了机器人的姿态矩阵, 最后一列 p 反应了机器人在空间中的位置:...
OpenGL入门002——顶点着色器和片段着色器
文章目录 一些概念坐标转换阶段顶点着色器片段着色器VBOVAO 实战简介main.cppCMakeLists.txt最终效果 一些概念 坐标转换阶段 概述: 模型空间、世界空间、视图空间和裁剪空间是对象在3D场景中经历的不同坐标变换阶段。每个空间对应渲染管道的一个步骤,…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...
