动态规划——两个数组的dp问题
目录
一、最长公共子序列
二、不同的子序列
三、通配符匹配
四、正则表达式匹配
五、两个字符串的最小ASCII删除和
六、最长重复子数组
七、交错字符串
一、最长公共子序列
最长公共子序列

第一步:确定状态表示
dp[i][j]:表示字符串 s1 的 [0,i] 区间以及字符串 s2 的[0,j] 区间内所有子序列中,最长公共子序列的长度。
第二步:推出状态转移方程

第三步:初始化dp表
关于字符串的 dp 问题,我们需要考虑空串的情况,比如 s1 选一个空串,s2 选一个空串,其实也属于是一个公共子序列,不过公共子序列长度为0。
我们可以在原始 dp 表上多加一行一列,第0行表示第一个字符串为空,第0列表示第二个字符串为空。

让dp表多加了一行和一列后,我们需要注意dp表的下标和字符串下标的对应关系。
解题代码:
class Solution
{
public:int longestCommonSubsequence(string s1, string s2) {int m = s1.size(), n = s2.size();vector<vector<int>> dp(m+1, vector<int>(n+1));for(int i = 1; i <= m; i++){for(int j = 1; j <= n; j++){if(s1[i-1] == s2[j-1])dp[i][j] = dp[i-1][j-1] + 1;elsedp[i][j] = max(dp[i-1][j], max(dp[i][j-1], dp[i-1][j-1]));}}return dp[m][n];}
}; 
二、不同的子序列
不同的子序列

第一步:确定状态表示
dp[i][j]:表示s字符串 [0,i]区间内所有子序列中,有多少个t字符串 [0,j] 区间内的子串。
第二步:推出状态转移方程

第三步:初始化dp表。
我们需要考虑空串的情况,比如 s1 选一个空串,s2 选一个空串,其实也属于是一个公共子序列。
第一行表示 s 字符串为空串,s 如果是空串,t 只有是空串,才能在 s 中找到 t。第一列表示 t 字符串为空串,t 如果是空串,s 不管是什么字符串,它里面都有一个空串。因此第一列应该全都是1。

解题代码:
class Solution
{
public:int numDistinct(string s, string t){int m = s.size(), n = t.size();vector<vector<double>> dp(m+1, vector<double>(n+1));for(int i = 0; i <= m; i++)dp[i][0] = 1;for(int i = 1; i <= m; i++){for(int j = 1; j <= n; j++){dp[i][j] += dp[i-1][j];if(s[i-1] == t[j-1])dp[i][j] += dp[i-1][j-1];}}return dp[m][n];}
}; 
三、通配符匹配
通配符匹配

第一步: 确定状态表示
dp[i][j]:表示p[0,i] 区间内的子串能否匹配 s[0,j] 区间内的子串。
第二步:推出状态转移方程

第三步:初始化dp表
如果s是空字符串,p字符串前面出现 ’ * ‘ 可以匹配空串,但是 ’ * ‘ 之后如果出现其他字符了,后面不管有多少个’ * '都不能匹配了。

dp[i][j]表示p[0,i] 区间内的子串能否匹配 s[0,j] 区间内的子串。题目要求是整个字符串,因此返回dp[m][n],m是s的长度,n是p的长度。
解题代码:
class Solution
{
public:bool isMatch(string s, string p) {int m = p.size(), n = s.size();vector<vector<bool>> dp(m+1, vector<bool>(n+1, false));dp[0][0] = true;for(int i = 1; i <= m; i++){if(p[i-1] == '*')dp[i][0] = true;elsebreak;}for(int i = 1; i <= m; i++){for(int j = 1; j <= n; j++){if(p[i-1] == '?')dp[i][j] = dp[i-1][j-1];else if(p[i-1] == '*')dp[i][j] = dp[i][j-1] || dp[i-1][j];else{if(p[i-1] == s[j-1] && dp[i-1][j-1])dp[i][j] = true;}}}return dp[m][n];}
}; 
四、正则表达式匹配
正则表达式匹配

第一步:确定状态表示
dp[i][j]:表示 p[0,i] 区间内的子串能否匹配 s[0,j] 区间内的字符串。
第二步:推出状态转移方程

第三步:初始化dp表
dp表上面多加一行表示p是空串,左边多加一列表示s是空串。接下来看看里面值应该填什么。
对于第一行,如果p是空串,s也是空串,肯定能匹配,所以第一行第一个空格还是true。
后续如果 p 是空串,s不是空串,肯定匹配不上,所以第一行后续都是false。

解题代码:
class Solution
{
public:bool isMatch(string s, string p) {int m = p.size(), n = s.size();vector<vector<bool>> dp(m+1, vector<bool>(n+1));dp[0][0] = true;s = ' ' + s;p = ' ' + p;for(int i = 2; i <= m; i++){if(p[i] != '*' && p[i-1] != '*')break;if(p[i] == '*' && p[i-1] != '*')dp[i][0] = true;}for(int i = 1; i <= m; i++){for(int j = 1; j <= n; j++){if(p[i] >= 'a' && p[i] <= 'z'){if(p[i] == s[j] && dp[i-1][j-1] == true)dp[i][j] = true;}else if(p[i] == '.')dp[i][j] = dp[i-1][j-1];else{if(p[i-1] == '.')dp[i][j] = dp[i-2][j] || dp[i][j-1];elsedp[i][j] = dp[i-2][j] || (s[j] == p[i-1] && dp[i][j-1]);}}}return dp[m][n];}
}; 
五、两个字符串的最小ASCII删除和
两个字符串的最小ASCII删除和

预处理:本道题是让我们找使两个字符串相等,所需删除字符的ASCII值最小。而最开始的两个字符串的ASCII值总和是不变的,那么我们只需要找到两个字符串相同后,其ASCII值最大,那么删除的字符的ASCII值一定就是最小的。
所以说,该问题就转化成了:求两个字符串的所有公共子序列里面,ASCII值的最大和。
第一步:确定状态表示
dp[i][j]:表示字符串 s1 的 [0,i] 区间以及字符串 s2 的 [0,j] 区间内的所有公共子序列中, ASCII值最大和。
第二步:推出状态转移方程
对于s1[0,i]区间和s2[0,j]区间的公共子序列有四种情况,即:
有s1[i],有s2[j]
有s1[i],没有s2[j]
没有s1[i],有s2[j]
没有s1[i],没有s2[j]
情况四可以包含在情况二中。

第三步:初始化dp表

第四步:确定返回值
状态表示求的是两个字符串的区间里面公共子序列的ASCII值最大和。
而题目要求使两个字符串相等所需删除字符的ASCII值的最小和 。所以可以这样做:
1、找到两个字符串中公共子序列的Ascll 最大和,dp[m][n]。
2、统计两个字符串中ASCII值总和,sum。
3、sum - dp[m][n] * 2。
解题代码:
class Solution
{
public:int minimumDeleteSum(string s1, string s2) {int m = s1.size(), n = s2.size();vector<vector<int>> dp(m+1, vector<int>(n+1));for(int i = 1; i <= m; i++){for(int j = 1; j <= n; j++){if(s1[i-1] == s2[j-1])dp[i][j] = dp[i-1][j-1] + s1[i-1];dp[i][j] = max(dp[i][j], max(dp[i][j-1], dp[i-1][j]));}}int sum = 0;for(auto x : s1)sum += x;for(auto x : s2)sum += x;return sum - 2 * dp[m][n];}
}; 
六、最长重复子数组
最长重复子数组

第一步:确定状态表示
dp[i][j]:表示数组 nums1 中以 i 位置元素为结尾的所有的子数组以及数组 nums2 中以 j 位置元素为结尾的所有子数组中,最长公共子数组的长度。
第二步:推出状态转移方程

第三步:初始化dp表

填写顺序:根据状态转移方程。从上往下填写每一行。 最后的返回值是 dp 表里面的最大值。
解题代码:
class Solution
{
public:int findLength(vector<int>& nums1, vector<int>& nums2) {int m = nums1.size(), n = nums2.size();vector<vector<int>> dp(m+1, vector<int>(n+1));int ret = 0;for(int i = 1; i <= m; i++){for(int j = 1; j <= n; j++){if(nums1[i-1] == nums2[j-1])dp[i][j] = dp[i-1][j-1] + 1;ret = max(ret, dp[i][j]);}}return ret;}
};
七、交错字符串
交错字符串

预处理:为了下标对应,我们给每个字符串的前面都加上一个空格字符。
第一步:确定状态表示
dp[i][j]:表示s1[1,i]区间内的字符串和s2[1,j]区间内的字符串能不能拼成s3[1,i+j]区间内的字符串。
第二步:推出状态转移方程

第三步:初始化dp表

解题代码:
class Solution
{
public:bool isInterleave(string s1, string s2, string s3) {int m = s1.size(), n = s2.size();if(m+n != s3.size())return false;s1 = " " + s1;s2 = " " + s2;s3 = " " + s3;vector<vector<bool>> dp(m+1, vector<bool>(n+1));dp[0][0] = true;for(int i = 1; i <= n; i++){if(s2[i] == s3[i])dp[0][i] = true;elsebreak;}for(int i = 1; i <= m; i++){if(s1[i] == s3[i])dp[i][0] = true;elsebreak;}for(int i = 1; i <= m; i++){for(int j = 1; j <= n; j++){if(s1[i] == s3[i+j] && dp[i-1][j])dp[i][j] = true;else if(s2[j] == s3[i+j] && dp[i][j-1])dp[i][j] = true;}}return dp[m][n];}
}; 
相关文章:

动态规划——两个数组的dp问题
目录 一、最长公共子序列 二、不同的子序列 三、通配符匹配 四、正则表达式匹配 五、两个字符串的最小ASCII删除和 六、最长重复子数组 七、交错字符串 一、最长公共子序列 最长公共子序列 第一步:确定状态表示 dp[i][j]:表示字符串 s1 的 [0&am…...

视频QoE测量学习笔记(二)
目录 自适应比特率(ABH或ABS) HAS:HTTP adaptive streaming 自适应本质: HAS正在解决传统流协议中主要关注的几个方面: DASH标准化原因 HAS发展 编码: 影响HAS系统的四个主要问题: 一个健全的HAS方…...

RSA算法详解:原理与应用
RSA算法详解:原理与应用 RSA算法是现代密码学的基石之一,广泛应用于安全通信、数据加密和身份验证等领域。本文将详细介绍RSA算法的原理、实现步骤以及实际应用。 一、RSA算法概述 RSA(Rivest-Shamir-Adleman)算法由Ron Rivest…...

YOLOv6-4.0部分代码阅读笔记-effidehead_fuseab.py
effidehead_fuseab.py yolov6\models\heads\effidehead_fuseab.py 目录 effidehead_fuseab.py 1.所需的库和模块 2.class Detect(nn.Module): 3.def build_effidehead_layer(channels_list, num_anchors, num_classes, reg_max16, num_layers3): 1.所需的库和模块 impo…...
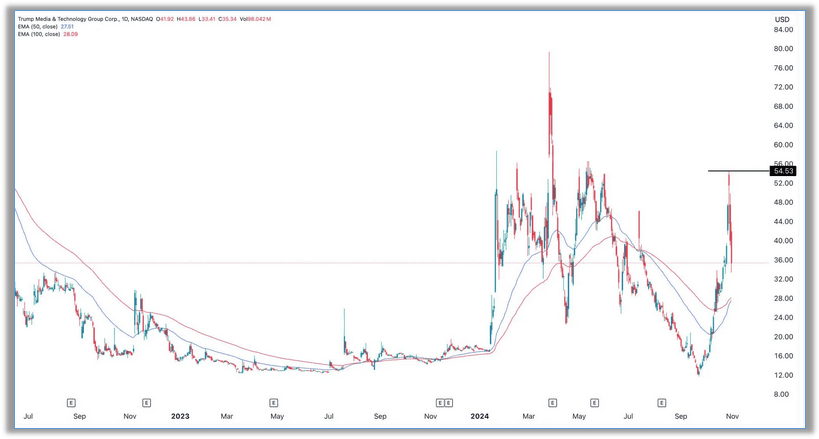
特朗普概念股DJT股票分析:为美国大选“黑天鹅事件”做好准备
猛兽财经核心观点: (1)特朗普媒体科技集团的股价近期已经从年初至今的高点下跌了35%以上。 (2)该公司将面临一个重大的黑天鹅事件。 (3)这一结果将对特朗普媒体科技集团产生重大影响。 随着投资…...

【MySQL】 运维篇—故障排除与性能调优:常见故障的排查与解决
数据库系统在运行过程中可能会遇到各种故障,如性能下降、连接失败、数据损坏等。及时有效地排查和解决这些故障,对于保证系统的稳定性和数据的完整性至关重要。 常见故障及排查方法 1. 数据库连接失败 故障描述:应用程序无法连接到数据库&…...

Android R S T U版本如何在下拉栏菜单增加基本截图功能
本文主要是MTK增加下拉栏开关菜单,功能实现为基本的截图功能,metrics_constants.proto修改 QuickSetting 新增快捷设置图标,以便对应getMetricsCategory获取;一个布局文件,一个配置加载合入实现,一个新增想要实现截图的类。 /frameworks/base/proto/src/metrics_constan…...

C#二叉树原理及二叉搜索树代码实现
一、概念 二叉树(Binary Tree)是一种树形数据结构,其中每个节点最多有两个子节点,分别称为左子节点和右子节点。二叉树的每个节点包含三个部分:一个值、一个指向左子节点的引用和一个指向右子节点的引用。 二、二叉树…...

.eslintrc.js 的解释
如果您的项目中没有 .eslintrc.js 文件,您可以按以下步骤创建并配置 ESLint: 1. 创建 ESLint 配置文件 在您的项目根目录下创建一个新的文件,命名为 .eslintrc.js。 2. 配置 ESLint 规则 在 .eslintrc.js 文件中添加以下内容,…...

确保企业架构与业务的一致性与合规性:数字化转型中的关键要素与战略实施
在现代企业的数字化转型过程中,确保企业架构(Enterprise Architecture, EA)与企业业务的紧密一致性与合规性至关重要。无论是在战略层面还是运营层面,EA都为企业的未来发展提供了清晰的蓝图,确保企业在应对复杂的业务环…...

goframe开发一个企业网站 前端界面 拆分界面7
将页面拆出几个公用部分 在resource/template/front创建meta.html header.html footer.html meta.html <head><meta charset"utf-8"><meta content"widthdevice-width, initial-scale1.0" name"viewport"><title>{{.…...

Postman断言与依赖接口测试详解!
在接口测试中,断言是不可或缺的一环。它不仅能够自动判断业务逻辑的正确性,还能确保接口的实际功能实现符合预期。Postman作为一款强大的接口测试工具,不仅支持发送HTTP请求和接收响应,还提供了丰富的断言功能,帮助测试…...

github打不开网络问题
当打开github出现超时或者网络不能访问的情况时,我们进行如下方法解决: 1,ping gitbub.com查看域名分析的DNS IP C:\Users\86156>ping github.com 正在 Ping github.com [20.205.243.166] 具有 32 字节的数据: 来自 20.205.243.166 的回复…...

智能教育工具:基于SpringBoot的在线试题库
1 绪论 1.1 研究背景 现在大家正处于互联网加的时代,这个时代它就是一个信息内容无比丰富,信息处理与管理变得越加高效的网络化的时代,这个时代让大家的生活不仅变得更加地便利化,也让时间变得更加地宝贵化,因为每天的…...

typescript 如何跳过ts类型检查?
文章目录 前言any类型条件判断进行使用断言加注释跳过ts检查 前言 typescript 的使用,虽然让代码更加规范,利于维护,但也给开发带来很多麻烦。为了跳过很多ts的类型检查,大家也是费尽心思,下面就介绍一些常用的方式&a…...

详解ReentrantLock--三种加锁方式
目录 介绍AQS: 直观方式解释加锁的流程: Node是什么:它里面有什么属性呢 图解队列的排队过程: 源码分析三种加锁流程: 我们先讲解一下非公平锁的加锁流程: Lock()方式加锁: 在源码里对于Lock()的解…...

SQL 基础语法(一)
文章目录 1. SQL 分类2. 数据库操作3. 数据表操作4. 增删改操作5. 查询操作6. 用户管理7. 权限控制 1. SQL 分类 2. 数据库操作 #创建数据库 create database if not exists test;#查询所有数据库 show databases;#查询当前数据库 select database();#删除数据库 drop databas…...

Python酷库之旅-第三方库Pandas(190)
目录 一、用法精讲 881、pandas.Index.is_方法 881-1、语法 881-2、参数 881-3、功能 881-4、返回值 881-5、说明 881-6、用法 881-6-1、数据准备 881-6-2、代码示例 881-6-3、结果输出 882、pandas.Index.min方法 882-1、语法 882-2、参数 882-3、功能 882-4、…...

Spring学习笔记_19——@PostConstruct @PreDestroy
PostConstruct && PreDestroy 1. 介绍 PostConstruct注解与PreDestroy注解都是JSR250规范中提供的注解。 PostConstruct注解标注的方法可以在创建Bean后在为属性赋值后,初始化Bean之前执行。 PreDestroy注解标注的方法可以在Bean销毁之前执行。 2. 依赖…...

《云计算网络技术与应用》实训8-1:OpenvSwitch简单配置练习
1.按《云计算网络技术与应用》实训5-1进行环境配置,安装好OVS 2.开启OVS虚拟交换机 3.创建一个网桥br0 4.查看网桥列表 5.把ens34网卡连接到网桥br0上 6. 查看网桥br0所有端口 7.列出网卡ens34连接的所有网桥列表 8.查看OVS网络状态 9.将网桥br0上连接的网卡ens34删…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...
