70B的模型需要多少张A10的卡可以部署成功,如果使用vLLM
部署一个 70B 的模型(如 defog/sqlcoder-70b-alpha)通常需要考虑多个因素,包括模型的内存需求和你的 GPU 配置。
1. 模型内存需求
大约计算,一个 70B 参数的模型在使用 FP16 精度时大约需要 280 GB 的 GPU 内存。对于 A10 GPU,其每张卡的显存大约为 24 GB。
2. 计算所需的 GPU 数量
为了计算所需的 A10 GPU 数量,可以使用以下公式:
[
\text{所需的 GPU 数量} = \frac{\text{模型内存需求 (GB)}}{\text{每张 GPU 的显存 (GB)}}
]
应用到我们的情况:
[
\text{所需的 GPU 数量} = \frac{280 \text{ GB}}{24 \text{ GB}} \approx 11.67
]
因此,你大约需要 12 张 A10 GPU 来成功部署这个模型。
3. vLLM 的支持
如果使用 vLLM,模型加载和并行处理可以通过多个 GPU 来优化,但每个 GPU 仍然需要足够的内存来承载模型的某些部分。因此,使用分布式训练或推理的方法也可能会有帮助。
4. 其他考虑
- 模型切分:使用模型并行来将模型切分到不同的 GPU 上。
- 混合精度:确保使用 FP16 或其他混合精度计算来节省内存。
- 负载均衡:合理配置负载均衡策略,以确保多个 GPU 的负载均匀。
总结,部署一个 70B 的模型至少需要 12 张 A10 GPU,并且需要合理配置和优化以确保有效利用资源。
相关文章:

70B的模型需要多少张A10的卡可以部署成功,如果使用vLLM
部署一个 70B 的模型(如 defog/sqlcoder-70b-alpha)通常需要考虑多个因素,包括模型的内存需求和你的 GPU 配置。 1. 模型内存需求 大约计算,一个 70B 参数的模型在使用 FP16 精度时大约需要 280 GB 的 GPU 内存。对于 A10 GPU&a…...

clickhouse配置用户角色与权限
首先找到user.xml文件,默认在/etc/clickhouse-server路径下 一、配置角色 找到标签定义 <aaaa><readonly>1</readonly><allow_dll>0</allow_dll> </aaaa>其中aaaa为角色名称,readonly为只读权限(0–代表…...

面试题整理 4
总结整理了某公司面试中值得记录的笔试和问到的问题和答案。 目录 PHP传值和传引用区别?什么情况下用传值?什么情况下用传引用? 传值 传引用 区别 选择传值还是传引用时 简述PHP的垃圾回收机制 二维数组排序 什么是CSRF攻击ÿ…...

React基础大全
文章目录 一、React基本介绍1.虚拟DOM优化1.1 原生JS渲染页面1.2 React渲染页面 2.需要提前掌握的JS知识 二、入门1.React基本使用2.创建DOM的两种方式2.1 使用js创建(一般不用)2.2 使用jsx创建 3.React JSX3.1 JSX常见语法规则3.2 for循环渲染数据 4.模…...

51c大模型~合集10
我自己的原文哦~ https://blog.51cto.com/whaosoft/11547799 #Llama 3.1 美国太平洋时间 7 月 23 日,Meta 公司发布了其最新的 AI 模型 Llama 3.1,这是一个里程碑时刻。Llama 3.1 的发布让我们看到了开源 LLM 有与闭源 LLM 一较高下的能力。 Meta 表…...

【已解决】element-plus配置主题色后,sass兼容问题。set-color-mix-level() is...in Dart Sass 3
项目:vue3vite "scripts": {"dev": "vite","build": "vite build","preview": "vite preview"},"dependencies": {"element-plus/icons-vue": "^2.3.1",&quo…...

JavaWeb——Web入门(4/9)-HTTP协议:请求协议(请求行、请求头、请求体、演示 )
目录 请求协议概述 请求行 请求头 请求体 演示 GET POST 请求协议概述 介绍完了 HTTP 协议的概念以及特点之后,接下来介绍 HTTP 当中的请求协议。 请求协议指的就是请求数据的格式。 HTTP 请求协议在整个 Web 通信中起着至关重要的作用。当用户在浏览器…...

软考:数据库考点总结
结构冲突 在数据库领域,冲突主要指的是在并发操作中,多个事务试图同时访问或修改相同的数据资源,导致数据一致性、完整性和隔离性受到威胁。以下是数据库中常见的几种冲突类型: 读写冲突(Read-Write Conflict…...

Flash的语音ic型号有哪些?
深圳唯创知音电子有限公司在语音技术领域具有深厚的积累,其Flash语音IC产品凭借高性能和广泛的应用领域,在市场上占据了一席之地。以下是对该公司Flash语音IC产品的详细介绍: 一、产品概述 Flash语音IC是一种采用Flash存储技术的语音芯片&…...

10天进阶webpack---(1)为什么要有webpack
首先就是我们的代码是运行在浏览器上的,但是我们开发大多都是利用node进行开发的,在浏览器中并没有node提供的那些环境。这就早成了运行和开发上的不同步问题。 -----引言 浏览器模块化的问题: 效率问题:精细的模块划分带来了更…...
HTML CSS
目录 1. 什么是HTML 2. 什么是CSS ? 3. 基础标签 & 样式 3.1 新浪新闻-标题实现 3.1.1 标题排版 3.1.1.1 分析 3.1.1.2 标签 3.1.1.3 实现 3.1.2 标题样式 3.1.2.1 CSS引入方式 3.1.2.2 颜色表示 3.1.2.3 标题字体颜色 3.1.2.4 CSS选择器 3.1.2.5 发布时间字…...
第03章 MySQL的简单使用命令
一、MySQL的登录 1.1 服务的启动与停止 MySQL安装完毕之后,需要启动服务器进程,不然客户端无法连接数据库。 在前面的配置过程中,已经将MySQL安装为Windows服务,并且勾选当Windows启动、停止时,MySQL也 自动启动、停止…...

【C++动态规划】2435. 矩阵中和能被 K 整除的路径|1951
本文涉及知识点 C动态规划 LeetCode2435. 矩阵中和能被 K 整除的路径 给你一个下标从 0 开始的 m x n 整数矩阵 grid 和一个整数 k 。你从起点 (0, 0) 出发,每一步只能往 下 或者往 右 ,你想要到达终点 (m - 1, n - 1) 。 请你返回路径和能被 k 整除的…...
三、Kafka集群
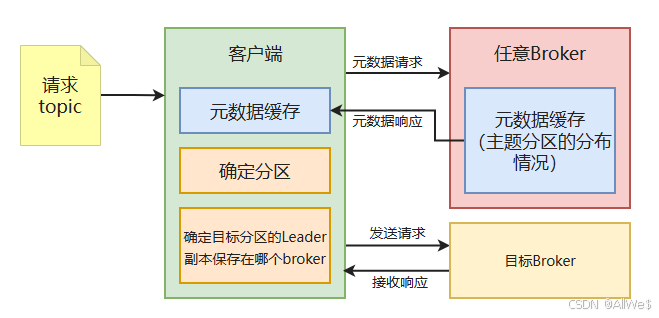
一、Kafka集群的概念 1、目的 高并发、高可用、动态扩展。 主备数据架构、双活节点、灾备数据中心。 如果是服务的地理范围过大也可以使不同的集群节点服务不同的区域,降低网络延迟。 2、Kafka集群的基本概念 1)复制(镜像) kaf…...

[数据结构]堆
堆,本质是一颗完全二叉树。属于非线性结构。 代码实现可参考树的代码。 函数介绍: //此堆是小堆,大堆操作部分与小堆相反 void InitHeap(Heap* cat) {assert(cat);cat->arr NULL;cat->capacity cat->size 0; } void DestroyHeap(Heap* cat) {assert(…...
UDP-鼠李糖合成酶基因的克隆与鉴定-文献精读76
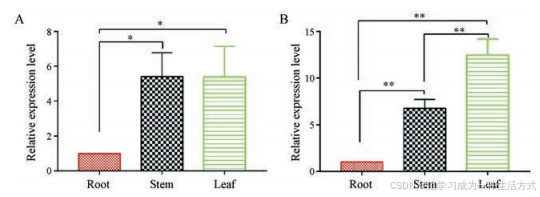
何首乌中UDP-鼠李糖合成酶基因FmRHM1/2的克隆与鉴定 摘要 UDP-鼠李糖是一种由UDP-鼠李糖合酶(RHM)催化合成的鼠李糖供体,而鼠李糖是鼠李糖苷化合物的重要组成部分,植物中只有少数基因编码的酶参与UDP-鼠李糖生物合成。本研究基于…...
Ajax)
【H2O2|全栈】JS进阶知识(四)Ajax
目录 前言 开篇语 准备工作 基本概念 原生JS使用AJAX 创建AJAX对象 设置请求方式和地址 设置请求头 发送请求 get方式发送 post方式发送 获取响应数据 AJAX状态码和HTTP状态消息 错误捕获 原生JS封装AJAX方法 $ 调用AJAX方法 结束语 前言 开篇语 本系列博客…...
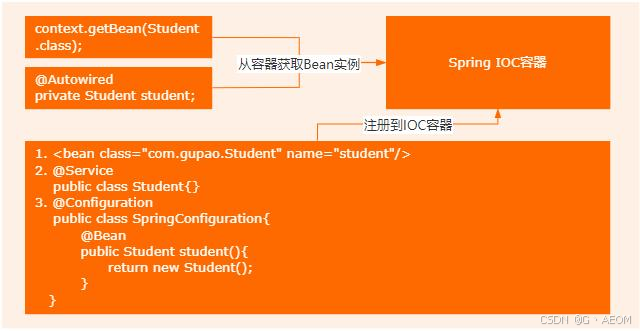
Spring IOC的工作流程
Spring IOC的工作流程 好的,这个问题我会从几个方面来回答。 IOC是什么 Bean的声明方式 IOC的工作流程 IOC的全称是 Inversion Of Control,也就是控制反转,它的核心思想是把对象的管理权限交给容器。(展示图 1) &…...
从新手到专家:7款电脑平面设计软件评测
平面设计在时尚、广告等多个领域扮演着重要角色,而创作出独特且富有创意的设计作品则需要依赖优秀的电脑平面设计软件。市场上的电脑平面设计软件众多,每款软件都有其独到之处。本文将为你推荐几款值得关注的电脑平面设计软件,并分析它们的特…...
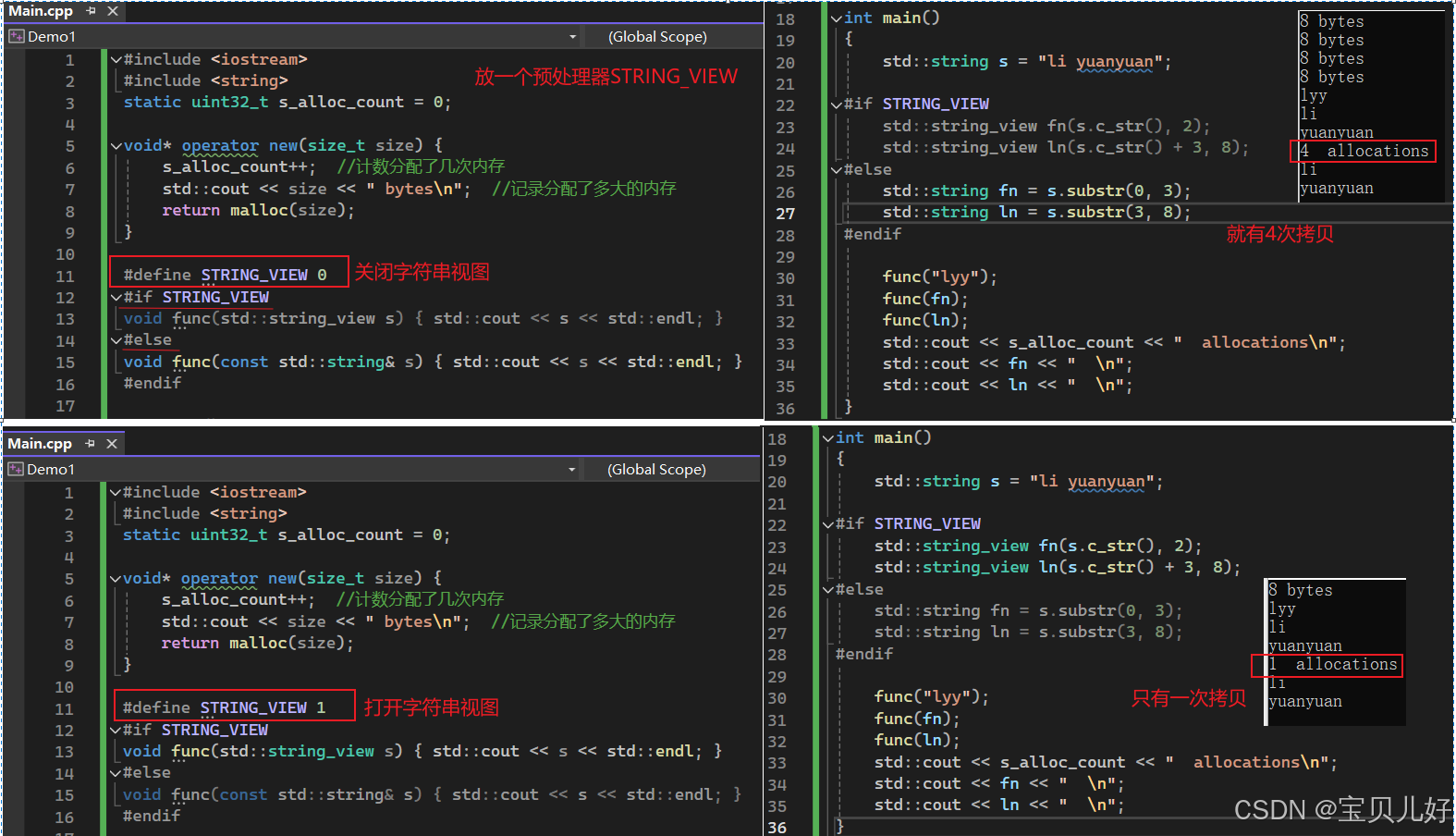
【C++】如何让C++字符串更快、C++的小字符串优化
二十三、如何让C字符串更快、C的小字符串优化 1、如何让C字符串更快? 如果程序中有很多字符串操作,比如格式化文本(日志记录),那是非常糟糕的,因为字符串操作是很慢的。字符串string和它相关的很多函数很可能会自动分配内存&…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...
