【C++动态规划】2435. 矩阵中和能被 K 整除的路径|1951
本文涉及知识点
C++动态规划
LeetCode2435. 矩阵中和能被 K 整除的路径
给你一个下标从 0 开始的 m x n 整数矩阵 grid 和一个整数 k 。你从起点 (0, 0) 出发,每一步只能往 下 或者往 右 ,你想要到达终点 (m - 1, n - 1) 。
请你返回路径和能被 k 整除的路径数目,由于答案可能很大,返回答案对 109 + 7 取余 的结果。
示例 1:

输入:grid = [[5,2,4],[3,0,5],[0,7,2]], k = 3
输出:2
解释:有两条路径满足路径上元素的和能被 k 整除。
第一条路径为上图中用红色标注的路径,和为 5 + 2 + 4 + 5 + 2 = 18 ,能被 3 整除。
第二条路径为上图中用蓝色标注的路径,和为 5 + 3 + 0 + 5 + 2 = 15 ,能被 3 整除。
示例 2:

输入:grid = [[0,0]], k = 5
输出:1
解释:红色标注的路径和为 0 + 0 = 0 ,能被 5 整除。
示例 3:

输入:grid = [[7,3,4,9],[2,3,6,2],[2,3,7,0]], k = 1
输出:10
解释:每个数字都能被 1 整除,所以每一条路径的和都能被 k 整除。
提示:
m == grid.length
n == grid[i].length
1 <= m, n <= 5 * 104
1 <= m * n <= 5 * 104
0 <= grid[i][j] <= 100
1 <= k <= 50
动态规划
动态规划的状态表示
dp[r][c][k] 记录从起点到达(r,c) 路径和%K == k的方案数。空间复杂度:O(mnk)
动态规划的转移方程
枚举前置状态(r,c,k)
(r1,c1)是(r+1,c)或(r,c+1)
dp[r1][c1][(k+grid[r1][c1])%K] += dp[r][c][k]
单个状态转移的时间复杂度是:O(1),** 总复杂度**:O(mnk)
动态规划的填表顺序
先行后列,行号和列号都从小到大。
由于只能下移,不能上移,所以行号小的一定是前置节点。由于只能右移,不能左移,所以行号相同,列号小的是前置节点。
动态规划的初始值
全部为0。
动态规划的返回值
dp.back().back()[0]
代码
核心代码
template<int MOD = 1000000007>
class C1097Int
{
public:C1097Int(long long llData = 0) :m_iData(llData% MOD){}C1097Int operator+(const C1097Int& o)const{return C1097Int(((long long)m_iData + o.m_iData) % MOD);}C1097Int& operator+=(const C1097Int& o){m_iData = ((long long)m_iData + o.m_iData) % MOD;return *this;}C1097Int& operator-=(const C1097Int& o){m_iData = (m_iData + MOD - o.m_iData) % MOD;return *this;}C1097Int operator-(const C1097Int& o){return C1097Int((m_iData + MOD - o.m_iData) % MOD);}C1097Int operator*(const C1097Int& o)const{return((long long)m_iData * o.m_iData) % MOD;}C1097Int& operator*=(const C1097Int& o){m_iData = ((long long)m_iData * o.m_iData) % MOD;return *this;}C1097Int operator/(const C1097Int& o)const{return *this * o.PowNegative1();}C1097Int& operator/=(const C1097Int& o){*this /= o.PowNegative1();return *this;}bool operator==(const C1097Int& o)const{return m_iData == o.m_iData;}bool operator<(const C1097Int& o)const{return m_iData < o.m_iData;}C1097Int pow(long long n)const{C1097Int iRet = 1, iCur = *this;while (n){if (n & 1){iRet *= iCur;}iCur *= iCur;n >>= 1;}return iRet;}C1097Int PowNegative1()const{return pow(MOD - 2);}int ToInt()const{return m_iData;}
private:int m_iData = 0;;
};class Solution {public:int numberOfPaths(vector<vector<int>>& grid, int K) {const int R = grid.size();const int C = grid[0].size();vector<vector<vector<C1097Int<>>>> dp(R, vector<vector<C1097Int<>>>(C, vector<C1097Int<>>(K)));dp[0][0][grid[0][0] % K] = 1;for (int r = 0; r < R; r++) {for (int c = 0; c < C; c++) {for (int k = 0; k < K; k++) {if (r + 1 < R) {dp[r + 1][c][(k + grid[r + 1][c]) % K] += dp[r][c][k];}if (c + 1 < C) {dp[r][c + 1][(k + grid[r][c + 1]) % K] += dp[r][c][k];}}}}return dp.back().back()[0].ToInt();}};
单元测试
vector<vector<int>> grid;int k;TEST_METHOD(TestMethod11){grid = { {5,2,4},{3,0,5},{0,7,2} }, k = 3;auto res = Solution().numberOfPaths(grid, k);AssertEx(2, res);}TEST_METHOD(TestMethod12){grid = { {0,0} }, k = 5;auto res = Solution().numberOfPaths(grid, k);AssertEx(1, res);}TEST_METHOD(TestMethod13){grid = { {7,3,4,9},{2,3,6,2},{2,3,7,0} }, k = 1;auto res = Solution().numberOfPaths(grid, k);AssertEx(10, res);}

扩展阅读
| 我想对大家说的话 |
|---|
| 工作中遇到的问题,可以按类别查阅鄙人的算法文章,请点击《算法与数据汇总》。 |
| 学习算法:按章节学习《喜缺全书算法册》,大量的题目和测试用例,打包下载。重视操作 |
| 有效学习:明确的目标 及时的反馈 拉伸区(难度合适) 专注 |
| 闻缺陷则喜(喜缺)是一个美好的愿望,早发现问题,早修改问题,给老板节约钱。 |
| 子墨子言之:事无终始,无务多业。也就是我们常说的专业的人做专业的事。 |
| 如果程序是一条龙,那算法就是他的是睛 |
| 失败+反思=成功 成功+反思=成功 |
视频课程
先学简单的课程,请移步CSDN学院,听白银讲师(也就是鄙人)的讲解。
https://edu.csdn.net/course/detail/38771
如何你想快速形成战斗了,为老板分忧,请学习C#入职培训、C++入职培训等课程
https://edu.csdn.net/lecturer/6176
测试环境
操作系统:win7 开发环境: VS2019 C++17
或者 操作系统:win10 开发环境: VS2022 C++17
如无特殊说明,本算法用**C++**实现。

相关文章:

【C++动态规划】2435. 矩阵中和能被 K 整除的路径|1951
本文涉及知识点 C动态规划 LeetCode2435. 矩阵中和能被 K 整除的路径 给你一个下标从 0 开始的 m x n 整数矩阵 grid 和一个整数 k 。你从起点 (0, 0) 出发,每一步只能往 下 或者往 右 ,你想要到达终点 (m - 1, n - 1) 。 请你返回路径和能被 k 整除的…...
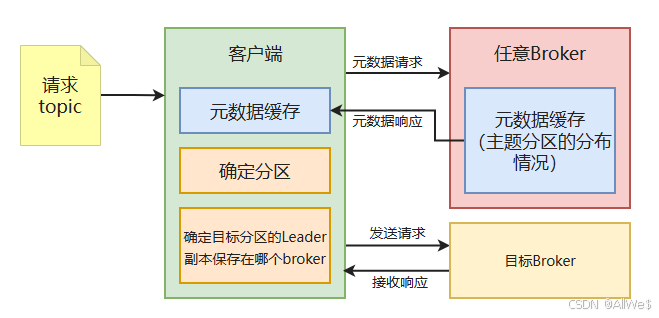
三、Kafka集群
一、Kafka集群的概念 1、目的 高并发、高可用、动态扩展。 主备数据架构、双活节点、灾备数据中心。 如果是服务的地理范围过大也可以使不同的集群节点服务不同的区域,降低网络延迟。 2、Kafka集群的基本概念 1)复制(镜像) kaf…...

[数据结构]堆
堆,本质是一颗完全二叉树。属于非线性结构。 代码实现可参考树的代码。 函数介绍: //此堆是小堆,大堆操作部分与小堆相反 void InitHeap(Heap* cat) {assert(cat);cat->arr NULL;cat->capacity cat->size 0; } void DestroyHeap(Heap* cat) {assert(…...
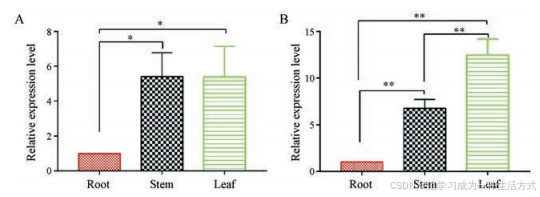
UDP-鼠李糖合成酶基因的克隆与鉴定-文献精读76
何首乌中UDP-鼠李糖合成酶基因FmRHM1/2的克隆与鉴定 摘要 UDP-鼠李糖是一种由UDP-鼠李糖合酶(RHM)催化合成的鼠李糖供体,而鼠李糖是鼠李糖苷化合物的重要组成部分,植物中只有少数基因编码的酶参与UDP-鼠李糖生物合成。本研究基于…...
Ajax)
【H2O2|全栈】JS进阶知识(四)Ajax
目录 前言 开篇语 准备工作 基本概念 原生JS使用AJAX 创建AJAX对象 设置请求方式和地址 设置请求头 发送请求 get方式发送 post方式发送 获取响应数据 AJAX状态码和HTTP状态消息 错误捕获 原生JS封装AJAX方法 $ 调用AJAX方法 结束语 前言 开篇语 本系列博客…...
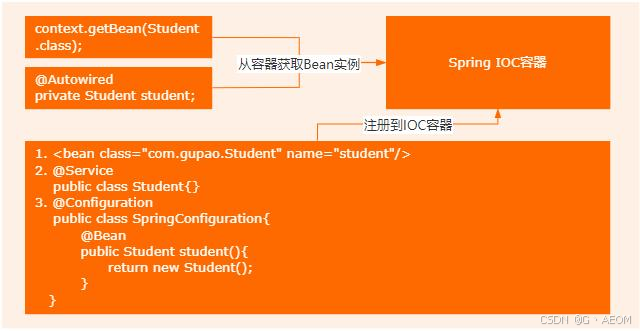
Spring IOC的工作流程
Spring IOC的工作流程 好的,这个问题我会从几个方面来回答。 IOC是什么 Bean的声明方式 IOC的工作流程 IOC的全称是 Inversion Of Control,也就是控制反转,它的核心思想是把对象的管理权限交给容器。(展示图 1) &…...
从新手到专家:7款电脑平面设计软件评测
平面设计在时尚、广告等多个领域扮演着重要角色,而创作出独特且富有创意的设计作品则需要依赖优秀的电脑平面设计软件。市场上的电脑平面设计软件众多,每款软件都有其独到之处。本文将为你推荐几款值得关注的电脑平面设计软件,并分析它们的特…...
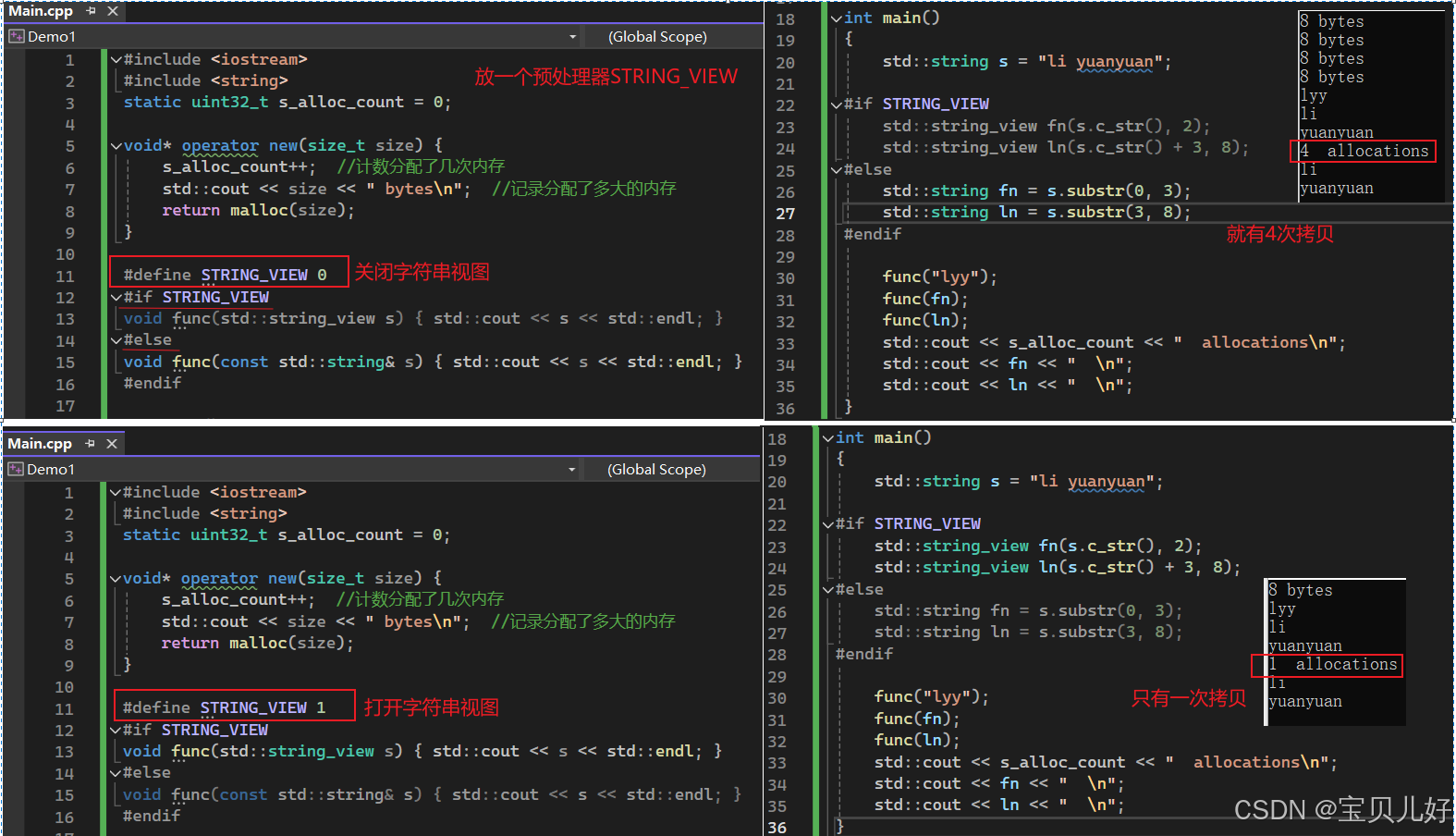
【C++】如何让C++字符串更快、C++的小字符串优化
二十三、如何让C字符串更快、C的小字符串优化 1、如何让C字符串更快? 如果程序中有很多字符串操作,比如格式化文本(日志记录),那是非常糟糕的,因为字符串操作是很慢的。字符串string和它相关的很多函数很可能会自动分配内存&…...

C++《list》
在本篇当中我们将学习STL中的list,在此list就是我们之前在数据结构学习过的链表,在本篇中我们要来了解list当中的成员函数该如何使用,由于list各个函数的接口和之前学习过的vector类型,因此在学习list的使用就较为轻松。在lis篇章…...

strongswan中METHOD定义
strongswan中使用METHOD来定义函数(方法),如下get_first函数定义。 METHOD(linked_list_t, get_first, status_t,private_linked_list_t *this, void **item) {if (this->count 0)return NOT_FOUND;*item this->first->value;ret…...
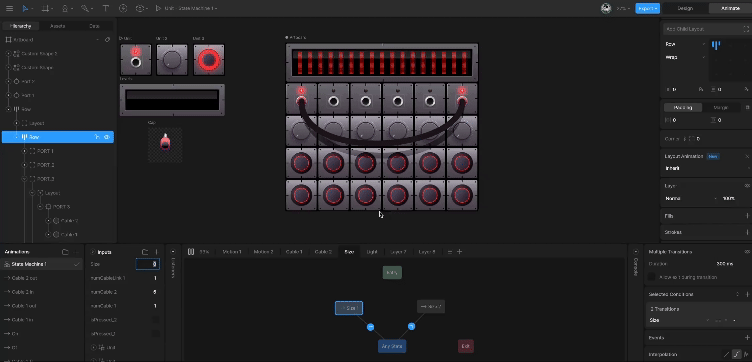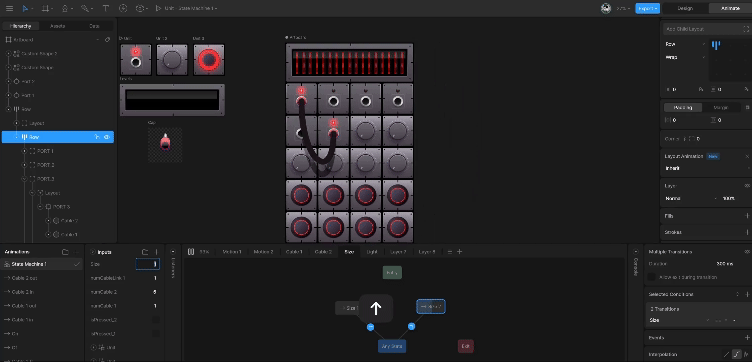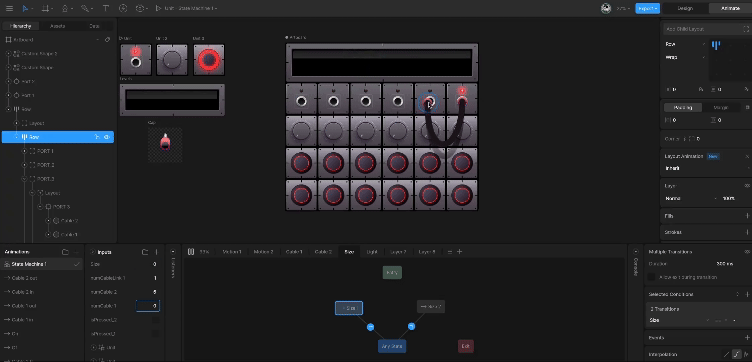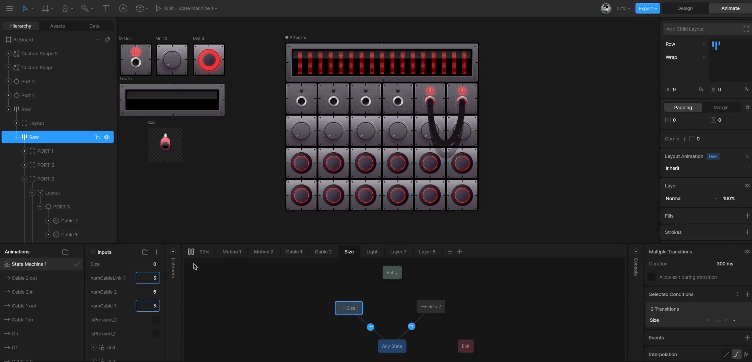
Rive 动画框架竟然支持响应式布局,全平台动画框架开启全新 UI 交互能力
没用过 Rive 的可能对于 Rive 还不熟悉,其实之前已经介绍过 Rive 好几次,例如《Rive 2 动画库「完全商业化」》 和《给掘金 Logo 快速添加动画效果》 等文章都介绍过 Rive ,之所以会接触 Rive 到, 也是因为多年前想在 Flutter 平台…...

MQ的详细大全知识点
MQ(Message Queue)是一种在分布式系统中广泛应用的消息中间件,它基于“先进先出”的数据结构原理,用于在不同系统之间传递消息。MQ通过提供接口给各个系统调用,实现了发送者和接收者之间的解耦,使得系统之间…...
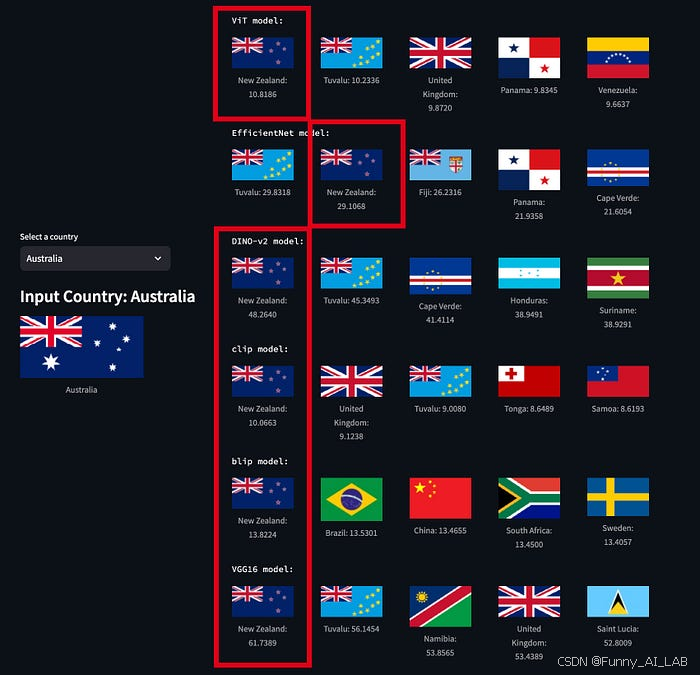
AI图像相似性搜索对比:VIT, CLIP, DINO-v2, BLIP-2
图像相似性搜索的核心在于一个简单的想法:图像可以表示为高维空间中的向量。当两个图像相似时,它们的向量应该在这个空间中占据相似的位置。我们可以通过测量角度(或余弦相似度)来确定这些向量的相似程度。如果角度小,…...
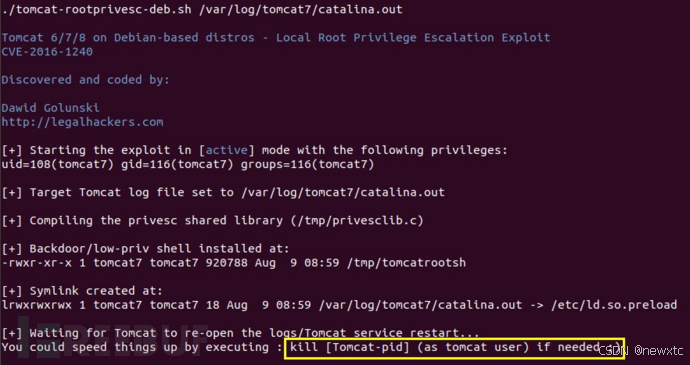
【tomcat系列漏洞利用】
Tomcat 服务器是一个开源的轻量级Web应用服务器,在中小型系统和并发量小的场合下被普遍使用。主要组件:服务器Server,服务Service,连接器Connector、容器Container。连接器Connector和容器Container是Tomcat的核心。一个Container…...
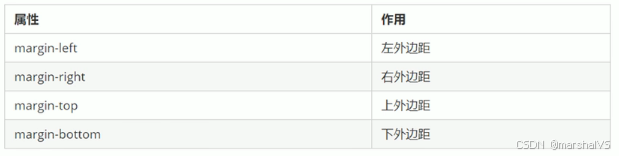
前端学习-盒子模型(十八)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 目录 前言 盒子模型组成 边框 语法 边框简写 代码示例 表格的细线边框 语法 内边距 内边距复合写法 外边距 外边距典型应用 外边距合并 清除内外边距 总结 前…...
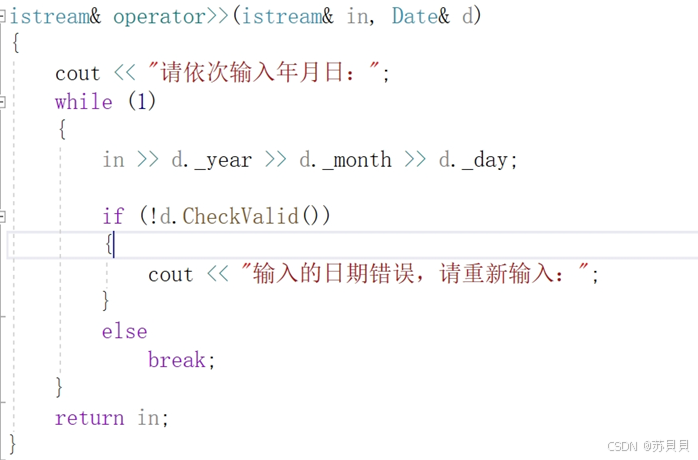
【C++】类和对象(十二):实现日期类
大家好,我是苏貝,本篇博客带大家了解C的实现日期类,如果你觉得我写的还不错的话,可以给我一个赞👍吗,感谢❤️ 目录 1 /!/>/</>/<运算符重载2 /-//-运算符重载(A) 先写,再通过写(B…...
文章解读与仿真程序复现思路——电网技术EI\CSCD\北大核心《提升系统频率支撑能力的“车-氢”柔性可控负荷协同构网控制》
本专栏栏目提供文章与程序复现思路,具体已有的论文与论文源程序可翻阅本博主免费的专栏栏目《论文与完整程序》 论文与完整源程序_电网论文源程序的博客-CSDN博客https://blog.csdn.net/liang674027206/category_12531414.html 电网论文源程序-CSDN博客电网论文源…...

异或的性质
交换两个变量的值,不使用第三个变量。 即a3,b5,交换之后a5,b3; 有两种解法, 一种用算术算法, 一种用^(异或) a a b; b a - b; a a - b; or a a^b;// 只能对int,char… b a^b; a a^b; or a ^ b ^ a; 异或交换两个变量值的方法是利用了异或运算的特性。下面是…...

新一代Webshell管理器
工具介绍 游魂是一个开源的Webshell管理器,提供更为方便的界面和更为简单易用的功能,可配合或代替其他webshell管理器,帮助用户在各类渗透场景中控制目标机器。游魂不仅支持常见的一句话webshell以及常见Webshell管理器的功能,还…...

「iOS」——知乎日报一二周总结
知乎日报仿写 前言效果Manager封装网络请求线程冲突问题下拉刷新添加网络请求的图片通过时间戳和日期格式化获取时间 总结 前言 前两周内容的仿写,主要完成了首页的仿写,进度稍慢。 效果 Manager封装网络请求 知乎日报的仿写需要频繁的申请网络请求&am…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...
