P11118 [ROI 2024 Day 2] 无人机比赛 题解
Description
有 n n n 架无人机参与比赛,第 i i i 架无人机飞过一个单位距离需 t i t_i ti 秒。
赛道为一条直线,上面有 m m m 个存档点,第 i i i 个存档点距起点 s i s_i si 个单位长度,保证 s i + 1 > s i s_{i+1}>s_i si+1>si。
一共有 n n n 场比赛,第 k k k 场比赛有前 k k k 架无人机参加,比赛按如下方式进行。
定义一个阶段为当前还未完赛的所有无人机从其存档点开始飞行,直到有一架无人机到达了下一个存档点,我们称这架无人机为此阶段的赢家。若有多架无人机同时到达,则编号最小的为赢家。
该阶段结束后,所有非赢家的无人机将被传送回此阶段开始时其所在的存档点,而赢家则更新其存档点。若赢家此时到达了第 m m m 个存档点,那么它将完赛,后面的阶段都不参加。
当所有无人机都完赛时,那么这场比赛就结束了。
你需要对于这 n n n 场比赛中的每一场,分别求出比赛中所有无人机的传送次数之和。
Solution
依题意得一个阶段中只有赢家改变存档点,对非赢家造成传送,而非赢家之间的相对位置都不改变,不会互相造成传送。
于是总传送次数可以拆成两两之间所造成的贡献之和,并且这只与它们两有多少个阶段输赢不同有关,即对于 i , j i,j i,j,两机互相造成的贡献为 i , j i,j i,j 中第一架无人机完赛时,已经经过了多少个阶段。
对于一架无人机 i i i,我们定义 w j = ( s j − s j − 1 ) × t i w_j=(s_j-s_{j-1})\times t_i wj=(sj−sj−1)×ti。
那么对于 i , j i,j i,j 算贡献,可以通过归并 i , j i,j i,j 的两个 w w w 序列来求出。然而 w w w 并不有序,但我们可以通过 UR #26 石子合并 中的结论,即对于同一序列的 w w w,若 w i + 1 ≤ w i w_{i+1}\le w_i wi+1≤wi 那么 w i + 1 w_{i+1} wi+1 会在 w i w_i wi 弹出后紧接地弹出,在归并后的数组中相邻。
而同一组中的 w w w 大小关系与 t t t 无关,与 s s s 的差分数组有关,所以可以对 s s s 的差分数组进行操作,将会紧邻弹出的数合在一起,设其总共有 k k k 个这样的段。每个段计 a i , b i a_i,b_i ai,bi,表示这一段段头的值以及这一段的长度。
因为 a i a_i ai 是严格递增的,那么由于 a 1 + a 2 + ⋯ + a k = s m ≤ 1.5 × 1 0 5 a_1+a_2+\cdots+a_k=s_m\le1.5\times10^5 a1+a2+⋯+ak=sm≤1.5×105,所以 k k k 的大小是 O ( V ) O(\sqrt{V}) O(V) 的, V V V 是 1.5 × 1 0 5 1.5\times10^5 1.5×105 级别的。
回到对 i , j ( i < j ) i,j(i<j) i,j(i<j) 算贡献,发现比较好算了:
-
t i ≤ t j t_i\le t_j ti≤tj,那么 i i i 先完赛,先加上 m m m 的贡献,即 i i i 对 j j j 造成的贡献。 j j j 对 i i i 造成的贡献就是看在 i i i 完赛时, j j j 到了第几个存档点,也就是找到最大的 x x x 使得 a k × t i > a x × t j a_k\times t_i>a_x\times t_j ak×ti>ax×tj,然后加上 b 1 + b 2 + ⋯ + b x b_1+b_2+\cdots+b_x b1+b2+⋯+bx 的贡献。
-
t i > t j t_i>t_j ti>tj,那么 j j j 先完赛,同样先加上 m m m 的贡献。然后找到最大的 x x x 使得 a x × t i ≤ a k × t j a_x\times t_i\le a_k\times t_j ax×ti≤ak×tj,同样加上 b 1 + ⋯ b x b_1+\cdots b_x b1+⋯bx 的贡献,注意是 小于等于,因为 i < j i<j i<j,所以当两人用时相等时赢家是 i i i。
找 x x x 用二分,那么至此我们用 O ( n 2 log V ) O(n^2\log\sqrt{V}) O(n2logV) 的复杂度解决了问题,比暴力分多 10 10 10 分,可喜可贺。
那么怎么继续优化呢?
考虑上扫描线,我们从小到大扫 i i i,对于每一个可能的 x x x,先二分找到 j j j 的限制(两种情况),再对这两段区间加上 b x b_x bx,注意我们已经把贡献分成了 m m m 和 b 1 + ⋯ + b x b_1+\cdots+b_x b1+⋯+bx。
计算答案就是扫到 j j j 时,取出其在线段树内的值,然后加上 j × ( j − 1 ) 2 × m \dfrac{j\times(j-1)}{2}\times m 2j×(j−1)×m 的贡献。
注意线段树上维护的是 离散后的 t t t 的值,二分也是找离散后的值,同时要 先算贡献再查值,不然若 t i = t j t_i=t_j ti=tj 时会重复算贡献。
现在时间复杂度变为了 O ( n V ( log n + log n ) ) O(n\sqrt{V}(\log n+\log n)) O(nV(logn+logn)),前面的 log \log log 是二分,后面的 log \log log 是区间修改,单点查询的线段树。但这个复杂度跑不过去,需要进一步优化。
注意到区间修改有 O ( n V ) O(n\sqrt{V}) O(nV) 级别,而询问只有 O ( n ) O(n) O(n) 级别,那么可以用区间修改 O ( 1 ) O(1) O(1),单点查询 O ( n ) O(\sqrt{n}) O(n) 的分块来平衡复杂度,具体的,维护每个点和每个块的差分数组,修改时修改两个点和两个块的值,查询即查询差分数组的前缀和。
但二分的 O ( log n ) O(\log n) O(logn) 还没去掉,观察到当 x x x 相同时, i i i 递增时,其对应 j j j 的限制也递增, i , j i,j i,j 是离散后 t t t 数组的下标。那么可以预处理出 t a g i , x tag_{i,x} tagi,x,表示二分出来的限制,用双指针维护做到时间 O ( n V ) O(n\sqrt{V}) O(nV),空间 O ( n V ) O(n\sqrt{V}) O(nV)。注意两种限制的双指针有所不同,细节较多。
这个题就用时间 O ( n ( V + n ) ) O(n(\sqrt{V}+\sqrt{n})) O(n(V+n)),空间 O ( n V ) O(n\sqrt{V}) O(nV) 的复杂度做完了,吗?
实际上 k k k 的极限并不是 1.5 × 1 0 5 \sqrt{1.5\times10^5} 1.5×105,而是 550 550 550 。所以开两个 t a g tag tag 会爆空间,不过只要先处理一种,算贡献,再处理另外一种,算贡献就可以了。
时间上有略微卡常,只需在求 t a g tag tag 时使访问较为连续即可,先枚 i i i,再枚 x x x。
还有一些细节具体见代码。
Code
#include<bits/stdc++.h>
using namespace std;
#define ll long long
int n,m,k,cnt,len;
int t[150010],s[150010],tt[150010],id[150010];
int tag[150010][560];
int st[150010],hd;
int a[560],b[560];
ll fin1[150010],fin2[560],ans[150010];
void init(){cin>>n>>m;for(int i=1;i<=n;i++){cin>>t[i],tt[i]=t[i];}sort(tt+1,tt+1+n);cnt=unique(tt+1,tt+1+n)-tt-1;len=sqrt(cnt)+1;for(int i=1;i<=n;i++){t[i]=lower_bound(tt+1,tt+1+cnt,t[i])-tt;}for(int i=1;i<=cnt+1;i++){id[i]=(i-1)/len+1;}for(int i=1;i<=m;i++){cin>>s[i];}for(int i=m;i;i--){while(hd&&s[st[hd]]-s[st[hd]-1]<=s[i]-s[i-1]) hd--;st[++hd]=i;}st[0]=m+1;for(int i=hd;i;i--){a[++k]=s[st[i]]-s[st[i]-1];b[k]=st[i-1]-st[i];}
}
void update(int l,int r,ll v){ //O(1)更新fin1[l]+=v,fin1[r+1]-=v;fin2[id[l]]+=v,fin2[id[r+1]]-=v;
}
ll query(int x){ //O(sqrt(n)) 查询ll sum=0;for(int i=1;i<id[x];i++){sum+=fin2[i];}for(int i=(id[x]-1)*len+1;i<=x;i++){sum+=fin1[i];}return sum;
}
void pres1(){ //ti<=tjfor(int j=1;j<=cnt;j++){for(int i=1;i<=k;i++){int fl=tag[j-1][i];while(1){tag[j][i]=fl;if(fl+1>cnt||(ll)tt[j]*a[k]<=(ll)tt[fl+1]*a[i]) break;fl++;}}}
}
void pres2(){ //ti>tj,两个双指针细节多,一定要理解充分for(int j=1;j<=cnt;j++){for(int i=1;i<=k;i++){int fl=tag[j-1][i];while(1){if((ll)tt[j]*a[i]<=(ll)a[k]*tt[fl]){tag[j][i]=fl;break;}fl++;}}}
}
void solve(){pres1();for(int i=1;i<=n;i++){ans[i]=query(t[i]);for(int j=1;j<=k;j++){if(tag[t[i]][j]>=t[i]){update(t[i],tag[t[i]][j],b[j]);}}}pres2();for(int i=1;i<=cnt;i++) fin1[i]=0; //记得清空分块for(int i=1;i<=id[cnt+1];i++) fin2[i]=0;for(int i=1;i<=n;i++){ans[i]+=ans[i-1]+query(t[i]);cout<<ans[i]+(ll)i*(i-1)/2*m<<'\n';for(int j=1;j<=k;j++){if(tag[t[i]][j]<t[i]){update(tag[t[i]][j],t[i]-1,b[j]);}}}
}
int main(){ios::sync_with_stdio(0);cin.tie(nullptr);init();solve();return 0;
}
相关文章:

P11118 [ROI 2024 Day 2] 无人机比赛 题解
Description 有 n n n 架无人机参与比赛,第 i i i 架无人机飞过一个单位距离需 t i t_i ti 秒。 赛道为一条直线,上面有 m m m 个存档点,第 i i i 个存档点距起点 s i s_i si 个单位长度,保证 s i 1 > s i s_{i1…...

时序数据库是什么:概念、特点与分类简析
时序数据与时序数据库的“保姆级”科普! 作为将数据价值转化为产能能效的“核心大脑”,数据库的发展依然处于加速期,面向不同数据类型的数据库类型也在不断增加。 在众多细分领域数据库类型中,伴随制造业数字化转型的行业趋势和多…...

大数据上岗.入职.就业面试题
1.海量日志数据,提取出某日访问阿里次数最多的那个IP 首先是这一天,并且是访问百度的日志中的IP取出来,逐个写入到一个大文件中。注意到ip是32位的,最多有个2^32个ip。同样可以采用映射的方法,比如模1000,把整个大文件映射为1000个小文件,在找出每个小文件中出现频率…...
2016年7月和8月NASA的气候成像(ATom)-1飞行活动期间测量的黑碳(BC)质量混合比(单位为ng BC / kg空气)
目录 简介 摘要 代码 引用 网址推荐 知识星球 机器学习 简介 ATom: Black Carbon Mass Mixing Ratios from ATom-1 Flights 该数据集提供了在2016年7月和8月NASA的气候成像(ATom)-1飞行活动期间测量的黑碳(BC)质量混合比&…...

python opencv3
三、图像预处理2 1、图像滤波 为图像滤波通过滤波器得到另一个图像。也就是加深图像之间的间隙,增强视觉效果;也可以模糊化间隙,造成图像的噪点被抹平。 2、卷积核 在深度学习中,卷积核越大,看到的信息越多࿰…...

git原理与上传
言: git是一个软件,gitee/github是一个网站,这里有什么联系吗?我们身为一个程序员不可能不知道github,但是毕竟这是外国的网站,我们不翻墙的情况下,是无法访问的(或者就是太慢了,或…...
)
LeetCode:633. 平方数之和(Java)
633. 平方数之和 题目描述: 给定一个非负整数 c ,你要判断是否存在两个整数 a 和 b,使得 a2 b2 c 。 示例 1: 输入:c 5 输出:true 解释:1 * 1 2 * 2 5示例 2: 输入…...

linux查看端口状态的命令合集
linux查看端口状态的命令合集 直接使用 netstat 命令 如果你不需要超级用户权限,可以直接运行 netstat 命令: netstat -tuln 使用 ss 命令 ss 是一个更现代的工具,通常不需要超级用户权限就能查看端口信息。你可以尝试使用 ss 命令ÿ…...

幼儿园篮球游戏
题目描述: 幼儿园里有一个放倒的圆桶,它是一个 线性结构,允许在桶的右边将篮球放入,可以在桶的左边和右边将篮球取出。每个篮球有单独的编号,老师可以连续放入一个或多个篮球,小朋友可以在桶左边或右边将篮…...

Android编译环境构建(二)(可用于物理机、虚拟机、容器化Jenkins环境)
文章目录 需求环境要求文件下载Gradle Version:7.5cmdline-tools至此普通物理环境的Android编译环境已部署完毕 部署maven(可选)Jenkins配置Android构建环境 说明: 物理环境:物理机、虚拟机等 容器化环境:docker等 需求 Gradle Version:7.5 …...

Web服务器(实验)
目录 nginx实验1(快速建站)实验2(更换默认网页目录)实验3(内网穿透花生壳)实验4(综合nginx)实验5(基于不同IP的虚拟主机网站)实验6(基于不同端口号…...

【湖南-常德】《市级信息化建设项目初步设计方案编制规范和支出预算编制标准(试行)》-省市费用标准解读系列05
《市级信息化建设项目初步设计方案编制规范和支出预算编制标准(试行)》(常行审 〔2023〕7号)标准是湖南省常德市行政审批服务局、常德市财政局2023年12月29日发布的费用标准(了解更多可直接关注我们咨询)。…...
微信小程序 https://pcapi-xiaotuxian-front-devtest.itheima.net 不在以下 request 合法域名
微信小程序在调用接口的时候出现以上报错,接口没有问题,是因为小程序自动校验了合法域名 打开本地设置: 勾选不校验合法域名,即可 效果如下:...

vue什么时候渲染旧的VDOM,什么时候渲染新的VDOM
在 Vue 中,决定渲染旧的 VDOM 还是新的 VDOM 的关键在于组件的数据变化和 Vue 的响应式系统。一些常见的情况可以帮助理解这个过程: 1. 渲染新 VDOM 的情况 数据变化:当组件的响应式数据(如 data、props 或计算属性)发…...
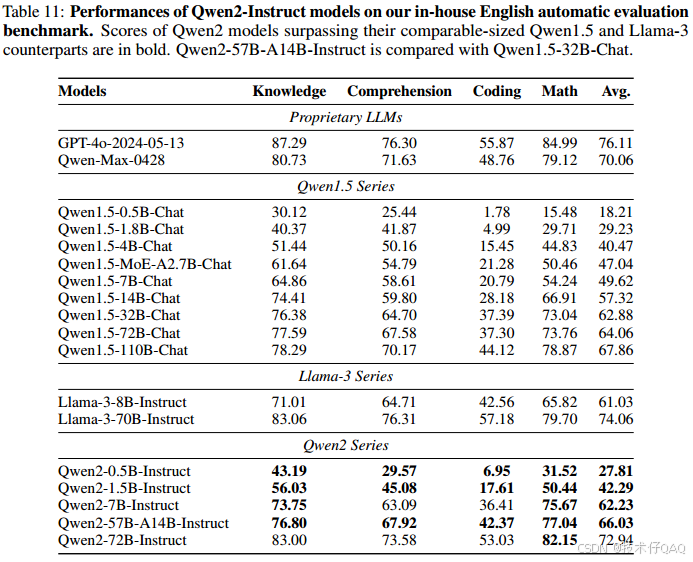
【Qwen2技术报告分析】从模型架构 数据构建和模型评估出发
目录 前言 一、Tokenizer 二、模型结构 dense模型 MoE模型 模型参数设置 三、Pre-Training Pre-Training DATA LONG-CONTEXT TRAINING 四、Post-Training Post-Training DATA 人工数据注释(collaborative data annotation) 自动数据合成&a…...
(鼠标悬停该条数据的时候展示全部内容))
Naive UI 选择器 Select 的:render-option怎么使用(Vue3 + TS)(鼠标悬停该条数据的时候展示全部内容)
项目场景: 在渲染select选择器后,当文字过长的时候,多出来的部分会显示成省略号,这使我们不能很清晰的看到该条数据的完整信息,就需要加一个鼠标悬停展示完整内容。 解决方案: vue代码: <n…...
使用Mac如何才能提高OCR与翻译的效率
OCR与截图大家都不陌生,或许有的朋友对于这两项功能用到的不多,但是如果经常会用到的话,那你就该看看了 iOCR,快捷键唤出翻译窗口,不论是截图翻译、划词翻译、输入翻译、剪切板翻译,统统快捷键完成&#x…...

QML----复制指定下标的ListModel数据
我现在有一个写好的listmodel,我需要从里边抽取35个数据作为展示 头文件 #ifndef GETONEPAGESIZEMEMBERLISTMODEL_H #define GETONEPAGESIZEMEMBERLISTMODEL_H#include <QObject> #include <QAbstractListModel> #include <QDebug> #include "mylistm…...
)
CSS Text(文本)
CSS Text(文本) CSS Text 是一种用于控制网页中文本显示样式的技术。通过使用 CSS Text 属性,开发者可以轻松地调整文本的字体、大小、颜色、对齐方式等,从而实现更加美观和个性化的网页设计。本文将详细介绍 CSS Text 的各种属性及其应用方法。 一、字体属性 1. font-fam…...
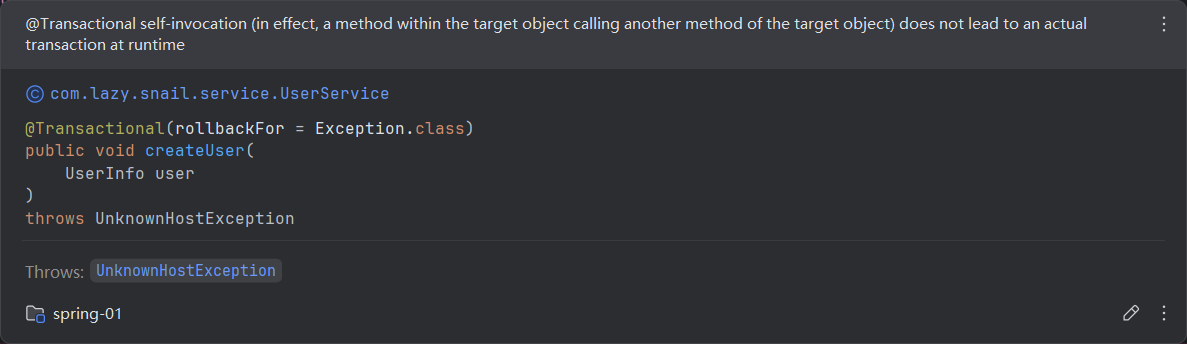
聊一聊Spring中的@Transactional注解【下】【注解失效场景】
前言 尽管 Transactional 注解在 Spring 中提供了方便的事务管理功能,我们在使用过程中却常常面临其失效的问题。事务失效可能导致意想不到的数据状态和错误,影响应用的稳定性和可靠性。本文将探讨一些常见的 Transactional 失效场景,包括异常…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

Vue 模板语句的数据来源
🧩 Vue 模板语句的数据来源:全方位解析 Vue 模板(<template> 部分)中的表达式、指令绑定(如 v-bind, v-on)和插值({{ }})都在一个特定的作用域内求值。这个作用域由当前 组件…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...

Java并发编程实战 Day 11:并发设计模式
【Java并发编程实战 Day 11】并发设计模式 开篇 这是"Java并发编程实战"系列的第11天,今天我们聚焦于并发设计模式。并发设计模式是解决多线程环境下常见问题的经典解决方案,它们不仅提供了优雅的设计思路,还能显著提升系统的性能…...
