算法笔记:Day-09(初始动态规划)
509. 斐波那契数
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1
F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
示例 1:
输入:n = 2
输出:1
解释:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:
输入:n = 3
输出:2
解释:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:
输入:n = 4
输出:3
解释:F(4) = F(3) + F(2) = 2 + 1 = 3
提示:
0 <= n <= 30
class Solution {public int fib(int n) {if(n<=1){return n;}int a=0,b=1,ans=0;for(int i=2;i<=n;i++){ans=a+b;a=b;b=ans;}return ans;}
}
70. 爬楼梯
-
假设你正在爬楼梯。需要
n阶你才能到达楼顶。每次你可以爬
1或2个台阶。你有多少种不同的方法可以爬到楼顶呢?示例 1:
输入:n = 2 输出:2 解释:有两种方法可以爬到楼顶。 1. 1 阶 + 1 阶 2. 2 阶示例 2:
输入:n = 3 输出:3 解释:有三种方法可以爬到楼顶。 1. 1 阶 + 1 阶 + 1 阶 2. 1 阶 + 2 阶 3. 2 阶 + 1 阶提示:
1 <= n <= 45
class Solution {public int climbStairs(int n) {int a=1,b=2;if(n==1)return a;if(n==2)return b;int ans=0;for(int i=3;i<=n;i++){ans=a+b;a=b;b=ans;}return ans;}
}
就是在一些最优子结构的基础上跳跃。
n==3时 有三种爬法 因为一次可以爬一阶或者两阶,所以在dp[1]的基础上跳两阶加上dp[2]跳一阶,就是两个最优子结构相加。
- 1 阶 + 2 阶
- 1 阶 + 1 阶 + 1 阶
- 2 阶 + 1 阶
55. 跳跃游戏
给你一个非负整数数组 nums ,你最初位于数组的 第一个下标 。数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标,如果可以,返回 true ;否则,返回 false 。
示例 1:
输入:nums = [2,3,1,1,4]
输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
输入:nums = [3,2,1,0,4]
输出:false
解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
提示:
1 <= nums.length <= 1040 <= nums[i] <= 105
class Solution {public boolean canJump(int[] nums) {int maxStep=0,len=nums.length;for(int i=0;i<len;i++){if(i>maxStep){return false;}maxStep=Math.max(maxStep,i+nums[i]);if(maxStep>=len-1){return true;}}return false;}
}
遍历数组更新最远距离,如果i超过了最远距离,说明跳不到 i 索引,即跳不到终点。
45. 跳跃游戏 II
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
0 <= j <= nums[i]i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
示例 1:
输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
示例 2:
输入: nums = [2,3,0,1,4]
输出: 2
class Solution {public int jump(int[] nums) {int len=nums.length;int maxStep=0;int end=0;int ans=0;for(int i=0;i<len-1;i++){maxStep=Math.max(maxStep,i+nums[i]);if(i==end){ans++;end=maxStep;}}return ans;}
}
338. 比特位计数
给你一个整数 n ,对于 0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案。
示例 1:
输入:n = 2
输出:[0,1,1]
解释:
0 --> 0
1 --> 1
2 --> 10
示例 2:
输入:n = 5
输出:[0,1,1,2,1,2]
解释:
0 --> 0
1 --> 1
2 --> 10
3 --> 11
4 --> 100
5 --> 101
class Solution {public int[] countBits(int n) {int[] ans=new int[n+1];int temp=0;for(int i=0;i<=n;i++){ans[i]=countOnes(i);}return ans;}public int countOnes(int x){int count=0;while(x!=0){x &= (x-1);count++;}return count;}
}
三种计算二进制中1的个数
- 利用位运算
public static int countOnes(int n) {int count = 0;while (n != 0) {count += n & 1; // 检查最低位是否为 1n >>>= 1; // 无符号右移 1 位}return count;}
- 利用内置方法
public class CountOnes {public static void main(String[] args) {int number = 29; // 例如:29 的二进制是 11101int count = Integer.bitCount(number);System.out.println("1 的个数: " + count);} }
- 利用Brian Kernighan 算法
public static int countOnes(int n) {int count = 0;while (n != 0) {n &= (n - 1); // 将最低位的 1 清零count++;}return count;}大佬的解法也不错
198. 打家劫舍
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
示例 1:
输入:[1,2,3,1]
输出:4
解释:偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入:[2,7,9,3,1]
输出:12
解释:偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。偷窃到的最高金额 = 2 + 9 + 1 = 12 。
解法一:
class Solution {public int rob(int[] nums) {int len=nums.length;int[] dp=new int[len];if(len==0)return 0;if(len==1)return nums[0];dp[0]=nums[0];dp[1]=Math.max(nums[0],nums[1]);for(int i=2;i<len;i++){dp[i]=Math.max(dp[i-1],dp[i-2]+nums[i]);}return dp[len-1];}
}
解法二:
class Solution {public int rob(int[] nums) {if (nums == null || nums.length == 0) {return 0;}int length = nums.length;int first=0,second=0;for (int i = 0; i < length; i++) {int temp = second;second = Math.max(first + nums[i], second);first = temp;}return second;}
}
解法二:因为每个最优子结构只与连两个房子有关。不需要考虑溢出问题,而且可以从0开始遍历,且空间复杂度为O(1)。
这个解法对于打家劫舍2有很大的优势。
213. 打家劫舍 II
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
示例 1:
输入:nums = [2,3,2]
输出:3
解释:你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。
示例 2:
输入:nums = [1,2,3,1]
输出:4
解释:你可以先偷窃 1 号房屋(金额 = 1),然后偷窃 3 号房屋(金额 = 3)。偷窃到的最高金额 = 1 + 3 = 4 。
示例 3:
输入:nums = [1,2,3]
输出:3
class Solution {public int rob(int[] nums) {if(nums.length == 0) return 0;if(nums.length == 1) return nums[0];return Math.max(myRob(Arrays.copyOfRange(nums, 0, nums.length - 1)), myRob(Arrays.copyOfRange(nums, 1, nums.length)));}private int myRob(int[] nums) {int pre = 0, cur = 0, tmp;for(int num : nums) {tmp = cur;cur = Math.max(pre + num, cur);pre = tmp;}return cur;}
}
这个解法简单优雅,不用考虑溢出问题。
class Solution {public int rob(int[] nums) {int len=nums.length;if(len==0)return 0;if(len==1)return nums[0];return Math.max(myRob(Arrays.copyOfRange(nums,0,len-1)),myRob(Arrays.copyOfRange(nums,1,len)));}public int myRob(int[] nums){int len=nums.length;int[] dp=new int[len];if(len==0)return 0;if(len==1)return nums[0];dp[0]=nums[0];dp[1]=Math.max(nums[0],nums[1]);for(int i=2;i<len;i++){dp[i]=Math.max(dp[i-1],dp[i-2]+nums[i]);}return dp[len-1];}
}
两个方法考虑溢出,因为如果
len==2的话myRob会出现溢出问题,烦死人了,如果时OI赛制我已经死了。
相关文章:

算法笔记:Day-09(初始动态规划)
509. 斐波那契数 斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) 0,F(1) 1 F(n) F(n - 1) F(n - 2),其中 …...

“探索未来医疗:生成式人工智能在医疗领域的革命性应用“
生成式人工智能(GenAI)在医疗领域的应用具有巨大的潜力和变革性,以下是一些关键的应用领域: 医学影像分析: GenAI模型通过深度学习技术,能够自动识别医学影像中的病变区域,提高诊断的准确性和速…...

数字IC后端实现Innovus 时钟树综合(Clock Tree Synthesis)典型案例
对于如下所示电路,要求以下几路做到等长,clock skew控制在50ps以内,clock tree insertion delay做到800ps! from FF/Q to FF1_1/D through the FF1 CK from FF/Q to FF2_1/D through the FF2 CK from FF/Q to FF3_1/D through the FF3 CK fr…...

Matlab应用制作入门
要在 MATLAB 中创建一个简单的应用程序,你可以使用 App Designer,这是一个用于构建交互式应用的工具。以下是一个简单的步骤,帮助你创建一个基本的 MATLAB 应用程序: 1. 打开 App Designer 在 MATLAB 命令窗口中输入 appdesigne…...

什么是声明式编程什么是函数式编程,打比方说明
在前端开发中,声明式编程和函数式编程是两种不同的编程范式,各自有其特定的理念和用法。下面详细介绍这两种编程范式,并通过比喻进行说明。 声明式编程 定义: 声明式编程是一种编程风格,强调“你想要什么”而不是“怎…...

SpringBoot+Shiro权限管理
Shiro是一个强大的Java安全框架,提供了身份验证、授权、加密、会话管理以及与Web集成等多种安全功能。以下是对Shiro权限管理的详细总结: 一、Shiro权限管理的基本概念 权限管理,一般指根据系统设置的安全规则或者安全策略,用户…...

前端面试题22 | 什么是跨域问题?怎么解决?
哈喽小伙伴们大家好!新的一周开始啦~距离2024年结束也仅有两个月了,不知道大家年初给自己制定的目标实现了多少?不管怎样,接下来的两个月都请继续加油哦!我们坚持下来了,我们就是最棒的! 今天,继续来给大家分享一道面试题 在开发中,我们经常会遇到跨域的问题,尤其是开发前后…...

HarmonyOS Next星河版笔记--界面开发(3)
属性 1.1.设计资源-svg图标 需求:界面中展示图标→可以使用的svg图标(任意放大缩小不失真、可以改变颜色) 使用方式: ①设计师提供:基于项目的图标,拷贝到项目目录使用 Image($r(app.media.ic_dianpu)) .width(40) fillColor…...

科研绘图系列:R语言组合连线图和箱线图(linechart+boxplot)
文章目录 介绍加载R包数据数据预处理画图1画图2系统信息介绍 连线图(Line Chart)是一种常用的数据可视化图表,它通过将一系列数据点用直线段连接起来来展示数据随时间或有序类别变化的趋势。以下是连线图可以表示的一些内容: 时间序列数据:展示数据随时间变化的趋势,例如…...

对象的接口与设计模式在其中的作用
对象的接口 对象的接口定义了对象的行为和如何与外界进行交互。以下是对象接口的详细解释: 成员函数(Member Functions) 定义:成员函数是定义在类中的函数,用于实现类的行为。成员函数可以通过对象来调用࿰…...

如何自学机器学习?
自学机器学习可以按照以下步骤进行: 一、基础知识准备 数学基础: 高等数学:学习微积分(包括导数、微分、积分等)、极限、级数等基本概念。这些知识是后续学习算法和优化方法的基础。 线性代数:掌握矩阵…...

python中应该使用while 1吗?按位运算符可以代替逻辑运算符使用吗?
while 1 很多初学者都很喜欢使用while 1,原因可能是,1只需要输入一个字符,更加“省事”,可以“偷懒”,并且,1看起来更加简洁明了。 实际上,在python中,while 1与while True是等价的…...
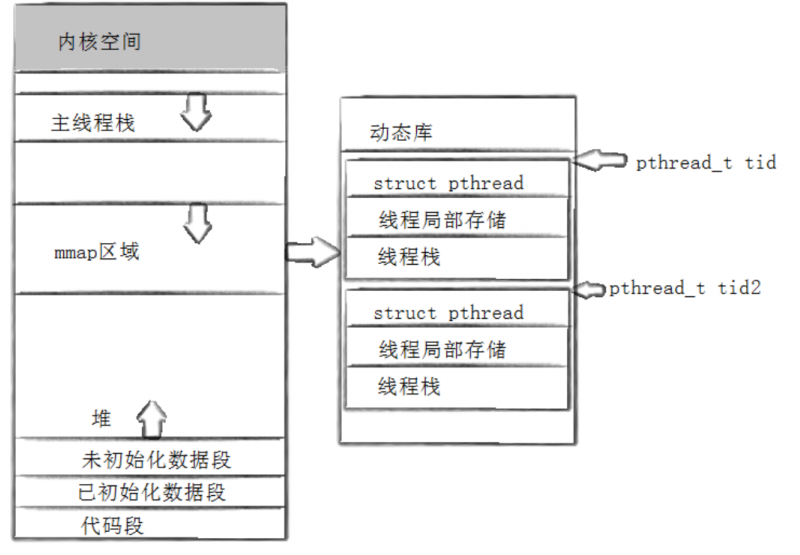
线程ID和线程库
在linux中,线程的运行可以用lwp来标识,只是操作系统的标识方法,lwp表示轻量级进程,在Linux中,进程和线程都可以用lwp来标识,而对于用户来说,也有对应的线程ID, 线程库 在linux中&a…...
使用AWS Lambda构建无服务器应用程序
💓 博客主页:瑕疵的CSDN主页 📝 Gitee主页:瑕疵的gitee主页 ⏩ 文章专栏:《热点资讯》 使用AWS Lambda构建无服务器应用程序 AWS Lambda 简介 创建 AWS 账户 创建 Lambda 函数 配置触发器 编写和测试代码 示例代码&am…...

响应式网页设计案例
文章目录 概念核心理念响应式设计的优点实现方法代码案例解释 概念 响应式设计核心理念是一个网站能够根据访问者的设备特性自动调整布局、内容和功能,以提供最佳的用户体验。它依赖于CSS媒体查询、灵活的网格布局和可伸缩的图像,确保网页内容在不同设备…...

麦麦Docker笔记(一)
本文记录如何零基础使用Docker Desktop。 使用操作系统为 macos 15.0.1 相关地址 docker官网 docker hub的镜像地址 下载docker desktop 前往官网下载,我用的macbook,下载的是apple 吸力根版本的,然后拖到application里完成安装ÿ…...

【设计模式系列】总览
努力填完如下表格ing... 设计模式简述详细链接单例模式(Singleton)工厂方法模式(Factory Method)简单工厂模式(Simple Factory Pattern)简单工厂模式是一个静态的工厂类,它提供一个根据参数决定…...

P11118 [ROI 2024 Day 2] 无人机比赛 题解
Description 有 n n n 架无人机参与比赛,第 i i i 架无人机飞过一个单位距离需 t i t_i ti 秒。 赛道为一条直线,上面有 m m m 个存档点,第 i i i 个存档点距起点 s i s_i si 个单位长度,保证 s i 1 > s i s_{i1…...

时序数据库是什么:概念、特点与分类简析
时序数据与时序数据库的“保姆级”科普! 作为将数据价值转化为产能能效的“核心大脑”,数据库的发展依然处于加速期,面向不同数据类型的数据库类型也在不断增加。 在众多细分领域数据库类型中,伴随制造业数字化转型的行业趋势和多…...

大数据上岗.入职.就业面试题
1.海量日志数据,提取出某日访问阿里次数最多的那个IP 首先是这一天,并且是访问百度的日志中的IP取出来,逐个写入到一个大文件中。注意到ip是32位的,最多有个2^32个ip。同样可以采用映射的方法,比如模1000,把整个大文件映射为1000个小文件,在找出每个小文件中出现频率…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

PH热榜 | 2025-06-08
1. Thiings 标语:一套超过1900个免费AI生成的3D图标集合 介绍:Thiings是一个不断扩展的免费AI生成3D图标库,目前已有超过1900个图标。你可以按照主题浏览,生成自己的图标,或者下载整个图标集。所有图标都可以在个人或…...

