为什么说高级工程师研究的不仅是器件的稳态,模拟器件的开关过程
高级工程师研究器件的开关过程而不仅仅是稳态,主要有以下几个原因:
1. 动态性能优化:开关过程中的特性,如上升时间、下降时间、过冲、振铃等,直接影响系统的性能。了解和优化这些动态特性对于提高系统的速度、精度和稳定性至关重要。
为什么说高级工程师研究的不仅是器件的稳态,模拟器件的开关过程
2. 电磁兼容性(EMC)考虑:在开关瞬间,电流和电压的快速变化会产生电磁干扰。研究开关过程有助于设计合适的滤波和屏蔽措施,以满足 EMC 标准,减少对其他设备的干扰,并提高自身系统的抗干扰能力。
3. 功耗管理:开关过程中的能量损耗通常比稳态时更为复杂和显著。精确分析开关过程可以更好地评估和控制功耗,对于节能和提高系统效率具有重要意义,特别是在电池供电或对功耗要求严格的应用中。
4. 可靠性和寿命预测:频繁的开关操作可能导致器件的热应力、电应力集中,从而影响其可靠性和使用寿命。深入研究开关过程有助于评估和预测器件的可靠性,采取相应的保护和散热措施,延长设备的使用寿命。
5. 系统级影响:在复杂的电路和系统中,一个器件的开关过程可能会对其他部分产生连锁反应。了解这些影响对于整体系统的设计和优化是必不可少的,以避免潜在的故障和性能下降。
6. 新技术和高频应用:随着技术的发展,特别是在高频和高速电路中,开关过程的特性对系统性能的影响更为突出。高级工程师需要紧跟这些趋势,深入研究开关过程以应对新的设计挑战。
综上所述,研究器件的开关过程能让高级工程师更全面、深入地理解和解决实际工程中的问题,从而设计出更优秀、可靠和高性能的系统。
相关文章:

为什么说高级工程师研究的不仅是器件的稳态,模拟器件的开关过程
高级工程师研究器件的开关过程而不仅仅是稳态,主要有以下几个原因: 1. 动态性能优化:开关过程中的特性,如上升时间、下降时间、过冲、振铃等,直接影响系统的性能。了解和优化这些动态特性对于提高系统的速度、精度和稳…...

Matlab实现白鲸优化算法(BWO)求解路径规划问题
目录 1.内容介绍 2.部分代码 3.实验结果 4.内容获取 1内容介绍 白鲸优化算法(BWO)是一种受自然界白鲸捕食行为启发的新型优化算法,它通过模拟白鲸的群体捕猎策略和社会互动来探索问题的最优解。BWO因其强大的全局搜索能力和高效的局部搜索能…...

SQLserver索引的优化和使用
在SQL Server中,索引的优化和有效使用是提高查询性能的关键。以下是一些详细的步骤和最佳实践,帮助你优化和使用索引。 1. 理解索引类型 聚集索引(Clustered Index) 定义:表中数据的物理排序顺序与索引的逻辑顺序相…...

Linux 安装nacos
1.下载版本 https://github.com/alibaba/nacos/tags 2.解压压缩包,启动 (1)将压缩包放到/usr/local目录下,解压 tar -xvf nacos-server-2.0.0-BETA.tar.gz(2)删除压缩包 rm -f nacos-server-2.0.0-BETA.tar.gz(3) 找到nacos的mysql的数据库脚本,在数…...

水仙花判断
一个三位整数,如果满足条件:个位数的立方十位数立方百位数立方这个数,那么称之为“水仙花数” 编程判断一个三位整数是不是水仙花数。 输入格式: 输入一个三位整数 输出格式: 是则输出YES,不是输出 NO (注意是大写字母…...

在VS中安装chatGPT
2、在VSCode中打开插件窗口 3、输入ChatGPT 4、这里有个ChatGPT中文版,就它了 5、安装 6、这时候侧边栏多了一个chatGPT分页图标,点击它 7、打个招呼 8、好像不行 9、看一下细节描述 10、根据要求按下按下快捷键 Ctrl Shift P 11、切换成国内模式 12、…...

算法笔记:Day-09(初始动态规划)
509. 斐波那契数 斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) 0,F(1) 1 F(n) F(n - 1) F(n - 2),其中 …...

“探索未来医疗:生成式人工智能在医疗领域的革命性应用“
生成式人工智能(GenAI)在医疗领域的应用具有巨大的潜力和变革性,以下是一些关键的应用领域: 医学影像分析: GenAI模型通过深度学习技术,能够自动识别医学影像中的病变区域,提高诊断的准确性和速…...

数字IC后端实现Innovus 时钟树综合(Clock Tree Synthesis)典型案例
对于如下所示电路,要求以下几路做到等长,clock skew控制在50ps以内,clock tree insertion delay做到800ps! from FF/Q to FF1_1/D through the FF1 CK from FF/Q to FF2_1/D through the FF2 CK from FF/Q to FF3_1/D through the FF3 CK fr…...

Matlab应用制作入门
要在 MATLAB 中创建一个简单的应用程序,你可以使用 App Designer,这是一个用于构建交互式应用的工具。以下是一个简单的步骤,帮助你创建一个基本的 MATLAB 应用程序: 1. 打开 App Designer 在 MATLAB 命令窗口中输入 appdesigne…...

什么是声明式编程什么是函数式编程,打比方说明
在前端开发中,声明式编程和函数式编程是两种不同的编程范式,各自有其特定的理念和用法。下面详细介绍这两种编程范式,并通过比喻进行说明。 声明式编程 定义: 声明式编程是一种编程风格,强调“你想要什么”而不是“怎…...

SpringBoot+Shiro权限管理
Shiro是一个强大的Java安全框架,提供了身份验证、授权、加密、会话管理以及与Web集成等多种安全功能。以下是对Shiro权限管理的详细总结: 一、Shiro权限管理的基本概念 权限管理,一般指根据系统设置的安全规则或者安全策略,用户…...

前端面试题22 | 什么是跨域问题?怎么解决?
哈喽小伙伴们大家好!新的一周开始啦~距离2024年结束也仅有两个月了,不知道大家年初给自己制定的目标实现了多少?不管怎样,接下来的两个月都请继续加油哦!我们坚持下来了,我们就是最棒的! 今天,继续来给大家分享一道面试题 在开发中,我们经常会遇到跨域的问题,尤其是开发前后…...

HarmonyOS Next星河版笔记--界面开发(3)
属性 1.1.设计资源-svg图标 需求:界面中展示图标→可以使用的svg图标(任意放大缩小不失真、可以改变颜色) 使用方式: ①设计师提供:基于项目的图标,拷贝到项目目录使用 Image($r(app.media.ic_dianpu)) .width(40) fillColor…...

科研绘图系列:R语言组合连线图和箱线图(linechart+boxplot)
文章目录 介绍加载R包数据数据预处理画图1画图2系统信息介绍 连线图(Line Chart)是一种常用的数据可视化图表,它通过将一系列数据点用直线段连接起来来展示数据随时间或有序类别变化的趋势。以下是连线图可以表示的一些内容: 时间序列数据:展示数据随时间变化的趋势,例如…...

对象的接口与设计模式在其中的作用
对象的接口 对象的接口定义了对象的行为和如何与外界进行交互。以下是对象接口的详细解释: 成员函数(Member Functions) 定义:成员函数是定义在类中的函数,用于实现类的行为。成员函数可以通过对象来调用࿰…...

如何自学机器学习?
自学机器学习可以按照以下步骤进行: 一、基础知识准备 数学基础: 高等数学:学习微积分(包括导数、微分、积分等)、极限、级数等基本概念。这些知识是后续学习算法和优化方法的基础。 线性代数:掌握矩阵…...

python中应该使用while 1吗?按位运算符可以代替逻辑运算符使用吗?
while 1 很多初学者都很喜欢使用while 1,原因可能是,1只需要输入一个字符,更加“省事”,可以“偷懒”,并且,1看起来更加简洁明了。 实际上,在python中,while 1与while True是等价的…...
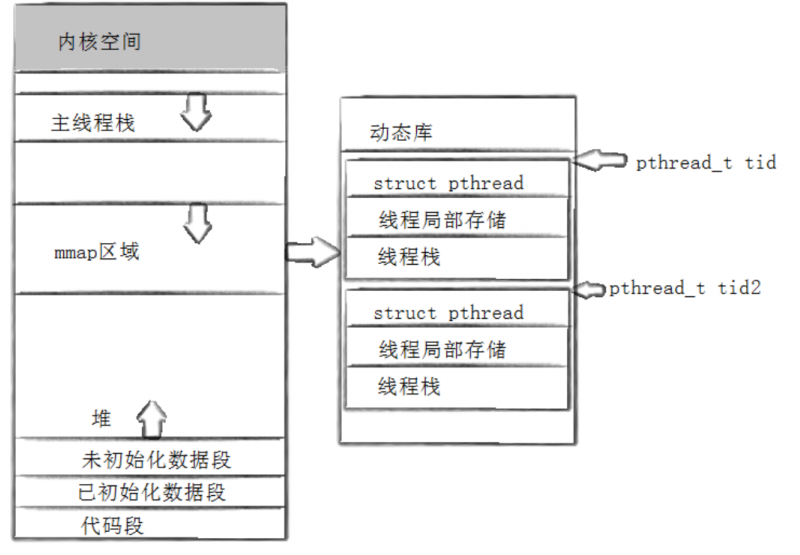
线程ID和线程库
在linux中,线程的运行可以用lwp来标识,只是操作系统的标识方法,lwp表示轻量级进程,在Linux中,进程和线程都可以用lwp来标识,而对于用户来说,也有对应的线程ID, 线程库 在linux中&a…...
使用AWS Lambda构建无服务器应用程序
💓 博客主页:瑕疵的CSDN主页 📝 Gitee主页:瑕疵的gitee主页 ⏩ 文章专栏:《热点资讯》 使用AWS Lambda构建无服务器应用程序 AWS Lambda 简介 创建 AWS 账户 创建 Lambda 函数 配置触发器 编写和测试代码 示例代码&am…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...
