文心一言 VS 讯飞星火 VS chatgpt (383)-- 算法导论24.5 3题
三、对引理 24.10 的证明进行改善,使其可以处理最短路径权重为 ∞ ∞ ∞ 和 − ∞ -∞ −∞ 的情况。引理 24.10(三角不等式)的内容是:设 G = ( V , E ) G=(V,E) G=(V,E) 为一个带权重的有向图,其权重函数由 w : E → R w:E→R w:E→R 给出,其源结点为 s s s 。那么对于所有的边 ( u , v ) ∈ E (u,v)∈E (u,v)∈E ,我们有 δ ( s , u ) ⩽ δ ( s , u ) + w ( u , v ) δ(s,u)⩽δ(s,u)+ w(u,v) δ(s,u)⩽δ(s,u)+w(u,v) 。如果要写代码,请用go语言。
文心一言:
为了处理最短路径权重为 ∞ ∞ ∞ 和 − ∞ -∞ −∞ 的情况,我们需要对三角不等式引理 24.10 的证明进行一定的调整。在这种情况下,我们需要特别注意权重的边界情况,即当路径不存在时,其权重应视为 ∞ ∞ ∞,而当路径权重为 − ∞ -∞ −∞ 时,也需要进行适当的处理。
下面是改进后的引理 24.10 的证明,以及使用 Go 语言实现的代码示例。
改进后的引理 24.10 证明
设 G = ( V , E ) G=(V,E) G=(V,E) 为一个带权重的有向图,其权重函数由 w : E → R w:E→R w:E→R 给出,其源结点为 s s s。我们需要证明对于所有的边 ( u , v ) ∈ E (u,v)∈E (u,v)∈E,有:
δ ( s , v ) ⩽ δ ( s , u ) + w ( u , v ) δ(s,v) \leqslant δ(s,u) + w(u,v) δ(s,v)⩽δ(s,u)+w(u,v)
其中 δ ( s , u ) δ(s,u) δ(s,u) 表示从源结点 s s s 到结点 u u u 的最短路径权重。如果路径不存在,则 δ ( s , u ) = ∞ δ(s,u) = ∞ δ(s,u)=∞。
证明:
-
基础情况:如果 δ ( s , u ) = ∞ δ(s,u) = ∞ δ(s,u)=∞,则 δ ( s , u ) + w ( u , v ) = ∞ δ(s,u) + w(u,v) = ∞ δ(s,u)+w(u,v)=∞,因为 w ( u , v ) w(u,v) w(u,v) 是有限的(可以是任意实数,包括 ∞ ∞ ∞ 和 − ∞ -∞ −∞,但在此上下文中,边的权重通常是有限的)。由于 δ ( s , v ) δ(s,v) δ(s,v) 最多为 ∞ ∞ ∞(如果路径不存在),因此不等式 δ ( s , v ) ⩽ δ ( s , u ) + w ( u , v ) δ(s,v) \leqslant δ(s,u) + w(u,v) δ(s,v)⩽δ(s,u)+w(u,v) 成立。
-
一般情况:假设 δ ( s , u ) δ(s,u) δ(s,u) 是有限的,即存在从 s s s 到 u u u 的路径。那么 δ ( s , v ) δ(s,v) δ(s,v) 要么是从 s s s 到 v v v 的直接路径(通过边 ( u , v ) (u,v) (u,v)),要么是通过其他路径到达 v v v。
- 如果 δ ( s , v ) δ(s,v) δ(s,v) 是通过边 ( u , v ) (u,v) (u,v) 到达的,则 δ ( s , v ) = δ ( s , u ) + w ( u , v ) δ(s,v) = δ(s,u) + w(u,v) δ(s,v)=δ(s,u)+w(u,v),不等式显然成立。
- 如果 δ ( s , v ) δ(s,v) δ(s,v) 不是通过边 ( u , v ) (u,v) (u,v) 到达的,则 δ ( s , v ) δ(s,v) δ(s,v) 必然小于或等于任何从 s s s 到 v v v 的其他路径的权重,包括通过 u u u 再到 v v v 的路径(即 δ ( s , u ) + w ( u , v ) δ(s,u) + w(u,v) δ(s,u)+w(u,v))。因此, δ ( s , v ) ⩽ δ ( s , u ) + w ( u , v ) δ(s,v) \leqslant δ(s,u) + w(u,v) δ(s,v)⩽δ(s,u)+w(u,v)。
-
特殊情况:如果 w ( u , v ) = − ∞ w(u,v) = -∞ w(u,v)=−∞,则 δ ( s , u ) + w ( u , v ) δ(s,u) + w(u,v) δ(s,u)+w(u,v) 可能为 − ∞ -∞ −∞。在这种情况下,如果 δ ( s , v ) δ(s,v) δ(s,v) 不是 − ∞ -∞ −∞,则必然存在一条从 s s s 到 v v v 的路径,其权重是有限的(不是 − ∞ -∞ −∞)。然而,由于我们可以总是选择通过 u u u 和 ( u , v ) (u,v) (u,v) 到达 v v v 来获得权重 − ∞ -∞ −∞(如果 δ ( s , u ) δ(s,u) δ(s,u) 不是 ∞ ∞ ∞),因此 δ ( s , v ) δ(s,v) δ(s,v) 实际上应该是 − ∞ -∞ −∞,使得不等式仍然成立。
Go 语言实现
以下是使用 Go 语言实现上述逻辑的示例代码:
package mainimport ("fmt""math"
)// 定义图的边
type Edge struct {From, To intWeight float64
}// 计算最短路径权重的函数(使用 Floyd-Warshall 算法作为示例)
func shortestPaths(graph [][]Edge, numVertices int) [][]float64 {// 初始化距离矩阵dist := make([][]float64, numVertices)for i := range dist {dist[i] = make([]float64, numVertices)for j := range dist[i] {if i == j {dist[i][j] = 0} else {dist[i][j] = math.Inf(1) // 初始化为正无穷大}}}// 设置边的权重for _, vertex := range graph {for _, edge := range vertex {dist[edge.From][edge.To] = edge.Weight}}// Floyd-Warshall 算法for k := 0; k < numVertices; k++ {for i := 0; i < numVertices; i++ {for j := 0; j < numVertices; j++ {if dist[i][k] != math.Inf(1) && dist[k][j] != math.Inf(1) && dist[i][k]+dist[k][j] < dist[i][j] {dist[i][j] = dist[i][k] + dist[k][j]}}}}return dist
}// 检查三角不等式
func checkTriangleInequality(graph [][]Edge, source int, numVertices int) {dist := shortestPaths(graph, numVertices)for _, vertex := range graph {for _, edge := range vertex {u, v := edge.From, edge.Tow := edge.WeightdeltaSU := dist[source][u]deltaSV := dist[source][v]fmt.Printf("Checking (%d, %d) with weight %f: δ(s,u) = %f, δ(s,v) = %f\n", u, v, w, deltaSU, deltaSV)if !(deltaSV <= deltaSU+w) {fmt.Printf("Triangle inequality violated for (%d, %d)!\n", u, v)} else {fmt.Println("Triangle inequality holds.")}}}
}func main() {// 示例图(邻接表表示)graph := [][]Edge{{{0, 1, 1.0}, {0, 2, 4.0}},{{1, 2, 2.0}, {1, 3, -math.Inf(1)}}, // 包含 -∞ 的边{{2, 3, 5.0}},{},}source := 0numVertices := len(graph)checkTriangleInequality(graph, source, numVertices)
}
在这个示例中,我们使用了 Floyd-Warshall 算法来计算最短路径权重,并检查三角不等式是否成立。注意,这个实现假设了边的权重可以是任意实数,包括 ∞ ∞ ∞ 和 − ∞ -∞ −∞。在实际应用中,你可能需要根据具体情况对算法进行调整,以处理特定的图结构和权重约束。




讯飞星火:
为了处理最短路径权重为 ∞ ∞ ∞ 和 − ∞ -∞ −∞ 的情况,我们需要对引理 24.10 进行一些修改。在带权重的有向图中,如果存在一条边的权重为 ∞ ∞ ∞ 或 − ∞ -∞ −∞,那么这条边的存在可能会影响最短路径的计算。
以下是改进后的引理 24.10 以及相应的 Go 语言代码实现:
改进后的引理 24.10
设 G = ( V , E ) G=(V,E) G=(V,E) 为一个带权重的有向图,其权重函数由 w : E → R w:E→R w:E→R 给出,其源结点为 s s s。对于所有的边 ( u , v ) ∈ E (u,v)∈E (u,v)∈E,我们有:
δ ( s , u ) + w ( u , v ) ≤ δ ( s , v ) δ(s,u) + w(u,v) \leq δ(s,v) δ(s,u)+w(u,v)≤δ(s,v)
其中, δ ( s , u ) δ(s,u) δ(s,u) 表示从源结点 s s s 到结点 u u u 的最短路径权重。
Go 语言代码实现
package mainimport ("fmt""math"
)// Edge represents a directed edge with a weight
type Edge struct {from intto intweight float64
}// Graph represents a directed graph with weights
type Graph struct {vertices intedges []Edge
}// BellmanFord implements the Bellman-Ford algorithm to find shortest paths from source vertex
func BellmanFord(graph *Graph, source int) ([]float64, error) {distance := make([]float64, graph.vertices)for i := range distance {distance[i] = math.Inf(1) // Initialize distances to infinity}distance[source] = 0 // Distance to the source is zero// Relax edges repeatedlyfor i := 0; i < graph.vertices-1; i++ {for _, edge := range graph.edges {if distance[edge.from] != math.Inf(1) && distance[edge.from]+edge.weight < distance[edge.to] {distance[edge.to] = distance[edge.from] + edge.weight}}}// Check for negative-weight cyclesfor _, edge := range graph.edges {if distance[edge.from] != math.Inf(1) && distance[edge.from]+edge.weight < distance[edge.to] {return nil, fmt.Errorf("graph contains a negative-weight cycle")}}return distance, nil
}func main() {// Example usage of Bellman-Ford algorithmgraph := &Graph{vertices: 5,edges: []Edge{{from: 0, to: 1, weight: 6},{from: 0, to: 2, weight: 7},{from: 1, to: 2, weight: 8},{from: 1, to: 3, weight: 5},{from: 1, to: 4, weight: -4},{from: 2, to: 3, weight: -3},{from: 2, to: 4, weight: 9},{from: 3, to: 1, weight: -2},{from: 4, to: 0, weight: 2},{from: 4, to: 3, weight: 7},},}source := 0distances, err := BellmanFord(graph, source)if err != nil {fmt.Println("Error:", err)} else {fmt.Println("Shortest path distances from source:", distances)}
}
解释
- Graph Representation: 我们使用
Edge结构体来表示有向边及其权重,并使用Graph结构体来表示整个图。 - Bellman-Ford Algorithm: 我们实现了 Bellman-Ford 算法来计算从源节点到所有其他节点的最短路径。该算法可以处理负权重边,并且能够检测负权重循环。
- Initialization: 初始化所有距离为无穷大(
math.Inf(1)),并将源节点的距离设置为0。 - Relaxation: 重复松弛所有边,更新最短路径估计值。
- Negative-Weight Cycle Check: 最后一步检查是否存在负权重循环。如果存在,则返回错误。
通过这种方式,我们可以处理最短路径权重为 ∞ ∞ ∞ 和 − ∞ -∞ −∞ 的情况,并确保算法的正确性和鲁棒性。
360智脑:
为了改进引理 24.10 的证明,使其能够处理最短路径权重为 ( \infty ) 和 ( -\infty ) 的情况,我们需要仔细考虑这些特殊情况下的行为。具体来说,我们需要确保在这些情况下,三角不等式仍然成立。
改进后的引理 24.10
引理 24.10 (改进的三角不等式):
设 ( G = (V, E) ) 为一个带权重的有向图,其权重函数由 ( w: E \to \mathbb{R} \cup {\infty, -\infty} ) 给出,其源结点为 ( s )。那么对于所有的边 ( (u, v) \in E ),我们有:
[ \delta(s, u) \leq \delta(s, v) + w(u, v) ]
其中,( \delta(s, u) ) 表示从源结点 ( s ) 到结点 ( u ) 的最短路径权重。
证明
-
基本情况:
- 如果 ( \delta(s, u) = \infty ),则不等式 ( \delta(s, u) \leq \delta(s, v) + w(u, v) ) 自然成立,因为任何数加上有限值或无穷大都不会小于无穷大。
- 如果 ( \delta(s, u) = -\infty ),则不等式 ( \delta(s, u) \leq \delta(s, v) + w(u, v) ) 也自然成立,因为负无穷大加上任何数仍然是负无穷大。
-
一般情况:
- 假设 ( \delta(s, u) ) 是有限值。
- 根据最短路径的定义,从 ( s ) 到 ( u ) 的最短路径权重 ( \delta(s, u) ) 不会大于从 ( s ) 到 ( v ) 的最短路径权重加上从 ( u ) 到 ( v ) 的边权重 ( w(u, v) )。
- 因此,我们有:
[ \delta(s, u) \leq \delta(s, v) + w(u, v) ]
Go 语言实现
以下是用 Go 语言实现的代码,用于验证改进后的三角不等式:
package mainimport ("fmt""math"
)// Weight represents the weight of an edge, which can be finite or infinite.
type Weight float64const (Infinity Weight = math.Inf(1)NegativeInfinity Weight = math.Inf(-1)
)// ShortestPathWeight represents the shortest path weight from source to a vertex.
type ShortestPathWeight map[string]Weight// Graph represents a weighted directed graph.
type Graph struct {Vertices []stringEdges map[string]map[string]WeightSource stringShortestPaths ShortestPathWeight
}// NewGraph creates a new graph with given vertices and edges.
func NewGraph(vertices []string, edges map[string]map[string]Weight, source string) *Graph {return &Graph{Vertices: vertices,Edges: edges,Source: source,ShortestPaths: make(ShortestPathWeight),}
}// InitializeShortestPaths initializes the shortest path weights from the source.
func (g *Graph) InitializeShortestPaths() {for _, v := range g.Vertices {if v == g.Source {g.ShortestPaths[v] = 0} else {g.ShortestPaths[v] = Infinity}}
}// Relax relaxes the edge (u, v) if a shorter path is found.
func (g *Graph) Relax(u, v string, weight Weight) {if g.ShortestPaths[u] + weight < g.ShortestPaths[v] {g.ShortestPaths[v] = g.ShortestPaths[u] + weight}
}// VerifyTriangleInequality verifies the triangle inequality for all edges.
func (g *Graph) VerifyTriangleInequality() bool {for u, neighbors := range g.Edges {for v, weight := range neighbors {if g.ShortestPaths[u] != NegativeInfinity && g.ShortestPaths[v] != Infinity {if g.ShortestPaths[u] > g.ShortestPaths[v]+weight {return false}}}}return true
}func main() {vertices := []string{"s", "u", "v"}edges := map[string]map[string]Weight{"s": {"u": 10},"u": {"v": 5},"v": {},}source := "s"graph := NewGraph(vertices, edges, source)graph.InitializeShortestPaths()// Relax edges to find shortest pathsgraph.Relax("s", "u", 10)graph.Relax("u", "v", 5)fmt.Println("Shortest Paths:", graph.ShortestPaths)fmt.Println("Triangle Inequality Verified:", graph.VerifyTriangleInequality())
}
解释
- Weight 类型: 定义了一个
Weight类型,它可以表示有限值、正无穷大和负无穷大。 - Graph 结构体: 表示一个带权重的有向图,包含顶点、边、源结点和最短路径权重。
- InitializeShortestPaths 方法: 初始化从源结点到所有顶点的最短路径权重。
- Relax 方法: 松弛边,更新最短路径权重。
- VerifyTriangleInequality 方法: 验证所有边是否满足改进后的三角不等式。
- main 函数: 创建图并初始化最短路径权重,松弛边,验证三角不等式。
通过这种方式,我们可以确保在处理最短路径权重为 ( \infty ) 和 ( -\infty ) 的情况下,三角不等式仍然成立。
智谱清言:
在处理最短路径权重为 ∞ ∞ ∞ 和 − ∞ -∞ −∞ 的情况时,我们需要首先明确几个前提:
如果源结点 s s s 到任何结点 u u u 的最短路径权重 δ ( s , u ) δ(s,u) δ(s,u) 为 ∞ ∞ ∞,那么这意味着在图中不存在从 s s s 到 u u u 的路径。
在大多数图算法中,权重 − ∞ -∞ −∞ 不是一个有效的权重,因为它会导致算法的不确定性。通常,我们假设权重函数 w w w 的值域是实数集中的有限值。
然而,如果我们必须处理 ∞ ∞ ∞ 和 − ∞ -∞ −∞ 的情况,我们可以对引理 24.10 的证明进行以下修改:
当 δ ( s , u ) = ∞ δ(s,u) = ∞ δ(s,u)=∞ 时,不等式 δ ( s , u ) ⩽ δ ( s , u ) + w ( u , v ) δ(s,u)⩽δ(s,u)+ w(u,v) δ(s,u)⩽δ(s,u)+w(u,v) 自然成立,因为 ∞ ∞ ∞ 加上任何数仍然是 ∞ ∞ ∞。
当 δ ( s , u ) = − ∞ δ(s,u) = -∞ δ(s,u)=−∞ 时,不等式可能不成立,因为 − ∞ -∞ −∞ 加上一个正数会变成一个小于 − ∞ -∞ −∞ 的数。然而,通常我们不会在图中使用 − ∞ -∞ −∞ 作为权重,因此这种情况在现实中不太可能出现。
以下是使用 Go 语言编写的代码示例,它考虑了 ∞ ∞ ∞ 的情况:
package main
import ("fmt""math"
)
// Edge represents a directed edge with a weight.
type Edge struct {from stringto stringweight float64
}
// Graph represents a weighted directed graph.
type Graph struct {edges map[string][]Edge
}
// NewGraph creates a new Graph.
func NewGraph() *Graph {return &Graph{edges: make(map[string][]Edge),}
}
// AddEdge adds a new edge to the graph.
func (g *Graph) AddEdge(from, to string, weight float64) {g.edges[from] = append(g.edges[from], Edge{from: from, to: to, weight: weight})
}
// ShortestPath calculates the shortest path from source to target.
func (g *Graph) ShortestPath(source, target string) float64 {dist := make(map[string]float64)for node := range g.edges {dist[node] = math.Inf(1) // Initialize distances with infinity}dist[source] = 0 // Distance to the source is 0// Relax edges repeatedlyfor {updated := falsefor _, edges := range g.edges {for _, edge := range edges {if dist[edge.from] != math.Inf(1) && dist[edge.from]+edge.weight < dist[edge.to] {dist[edge.to] = dist[edge.from] + edge.weightupdated = true}}}if !updated {break}}return dist[target]
}
func main() {g := NewGraph()g.AddEdge("s", "u", 1)g.AddEdge("u", "v", 2)g.AddEdge("s", "v", 4) // This edge should not be used in the shortest path from s to v// Check the triangle inequalitydistSU := g.ShortestPath("s", "u")distUV := g.ShortestPath("u", "v")distSV := g.ShortestPath("s", "v")// Check if the triangle inequality holds, considering infinityif distSV <= distSU+distUV || math.IsInf(distSU, 1) || math.IsInf(distUV, 1) {fmt.Println("Triangle inequality holds.")} else {fmt.Println("Triangle inequality does not hold.")}
}
在上述代码中,我们首先初始化所有结点的最短路径为 ∞ ∞ ∞,然后通过重复放松边来计算最短路径。在检查三角不等式时,我们考虑了 ∞ ∞ ∞ 的情况。如果 δ ( s , u ) δ(s,u) δ(s,u) 或 δ ( u , v ) δ(u,v) δ(u,v) 为 ∞ ∞ ∞,则不等式自然成立。如果都不是 ∞ ∞ ∞,我们再比较它们的大小。
天工:
- 分析问题
- 首先,原引理中的三角不等式在常规情况下成立。当要处理最短路径权重为(∞)和(-∞)的情况时,需要重新审视不等式中的各项含义。
- 对于(∞)的情况,如果(\delta(s, u)=\infty),那么(\delta(s, u)+w(u, v)=\infty)(当(w(u, v))为有限值时),不等式依然成立。如果(w(u, v)=\infty),也需要相应处理。
- 对于(-∞)的情况,当(\delta(s, u)=-\infty)或者(w(u, v)=-\infty)时,不等式的形式需要特殊处理,因为涉及到负无穷的加法运算。
- 改善证明思路(不涉及代码)
- 当(\delta(s, u)=\infty)时:
- 如果(w(u, v))是有限值,那么(\delta(s, u)+w(u, v)=\infty),显然(\delta(s, u)\leqslant\delta(s, u)+w(u, v))成立。
- 如果(w(u, v)=\infty),同样(\delta(s, u)\leqslant\delta(s, u)+w(u, v))成立。
- 当(\delta(s, u)=-\infty)时:
- 如果(w(u, v))是有限值,(\delta(s, u)+w(u, v)=-\infty),不等式(\delta(s, u)\leqslant\delta(s, u)+w(u, v))成立(两边都是(-\infty))。
- 如果(w(u, v)=-\infty),根据最短路径的定义和三角不等式的含义,在有向图的路径权重定义下,需要重新定义这种情况下不等式的意义,可能需要从图的结构和路径可达性角度去解释不等式依然成立(例如,从源点(s)到(u)的最短路径权重已经是负无穷,再加上到(v)的边权重,整体路径权重仍然是负无穷或者更负,不等式在这种广义的路径权重概念下成立)。
- 当(\delta(s, u))为有限值时:
- 如果(w(u, v))是有限值,原证明方法基本适用,只是需要明确在处理(∞)和(-∞)情况的框架下,这种常规情况的位置。
- 如果(w(u, v)=\infty),则(\delta(s, u)+w(u, v)=\infty),(\delta(s, u)\leqslant\delta(s, u)+w(u, v))成立。
- 如果(w(u, v)=-\infty),类似前面(\delta(s, u)=-\infty)的情况去处理,从路径权重的广义概念和图结构角度确保不等式成立。
- 当(\delta(s, u)=\infty)时:
- Go语言代码示例(假设图的结构已经定义,并且有计算(\delta)函数等相关函数)
package main// 假设这里有图的结构体定义以及相关的函数来获取边的权重和计算delta等// 这里只是一个伪代码框架,实际需要根据完整的图结构定义来完善
func checkTriangleInequality(s int, u int, v int, graph Graph) bool {delta_su := calculateDelta(s, u, graph)weight_uv := getWeight(u, v, graph)if delta_su == float64(+1<<63 - 1) {// 处理delta(s,u)为正无穷的情况if weight_uv == float64(+1<<63 - 1) {return true}return true} else if delta_su == float64(-1<<63) {// 处理delta(s,u)为负无穷的情况if weight_uv == float64(-1<<63) {// 根据前面的分析处理这种情况return true}return true} else {// 常规情况delta_sv := calculateDelta(s, v, graph)if delta_su <= delta_su+weight_uv {return true}return false}
}
请注意,上述代码中的Graph类型、calculateDelta函数和getWeight函数需要根据实际的图结构定义来实现。这个代码只是为了展示在处理(∞)和(-∞)情况时的大致框架。
chatgpt:
引理 24.10 的三角不等式可以表述为:在一个带权重的有向图中,源节点 ( s ) 到节点 ( u ) 的最短路径权重应当小于或等于从 ( s ) 到 ( u )、再加上从 ( u ) 到 ( v ) 的边的权重。这一定理本质上依赖于路径的加法性质,并且对于所有的节点及其之间的边有效。
要考虑最短路径权重为 ( \infty ) 和 ( -\infty ) 的情况,我们需要首先确定这些权重的意义:
-
最短路径权重为 ( \infty ):表示从源节点 ( s ) 到节点 ( u ) 不可达,因此 ( \delta(s, u) = \infty )。在这种情况下,任何加法 ( \delta(s, u) + w(u, v) ) 的结果也会是 ( \infty ),因此不等式仍然成立,因为
[
\infty \leq \infty
]
并且如果 ( \delta(s, u) = \infty ) 且 ( w(u, v) ) 是有限值,那么结果为 ( \infty ) 不等于真实路径的情况是讨论的一种边界情况。 -
最短路径权重为 ( -\infty ):表示存在路径可达性问题,通常会出现在有负权重环的情况下。这种情况下,我们常常会令最短路径标志为 ( -\infty ) 意味着在某个点之后开始无限缩小路径的权重,因此,对于所有延展的路径,构造出不等式的方式需要小心。
因此,在处理这些情况时,对引理 24.10 的表达和证明可以考虑如下逻辑:
改进的引理证明
对于每一条边 ( (u, v) \in E ),我们考虑以下几种情况:
-
假设 ( \delta(s, u) = \infty ):
- 由于 ( \delta(s, u) ) 是不可达的,那么对于任何值 ( w(u, v) ),
[
\delta(s, u) + w(u, v) = \infty + w(u, v) = \infty
]
不等式自然成立。
- 由于 ( \delta(s, u) ) 是不可达的,那么对于任何值 ( w(u, v) ),
-
假设 ( \delta(s, u) = -\infty ):
- 由于这里实际上意味着到达的路径存在负环,可形成无穷下降,因此所有后续添加 ( w(u, v) ) 的边也将导致总体路径权重趋近于负无穷,保持不等式成立。
-
假设 ( \delta(s, u) ) 和 ( w(u, v) ) 是有限值:
- 传统的三角不等式依旧成立:
[
\delta(s, u) + w(u, v) \text{ 结果也将是凡是 } \delta(s, v) \text{ 的可达性无影响}
]
- 传统的三角不等式依旧成立:
这种讨论确保了不等式在所有情况下均成立。
Go 语言实现
以下是简单的 Go 实现,可以帮助判断并在图中采用三角不等式进行更新:
package mainimport ("fmt""math"
)const inf = math.Inf(1) // 定义正无穷
const negInf = math.Inf(-1) // 定义负无穷// Graph 存储图的结构
type Graph struct {vertices intedges [][]float64
}// NewGraph 创建一个新图
func NewGraph(v int) *Graph {g := &Graph{vertices: v}g.edges = make([][]float64, v)for i := range g.edges {g.edges[i] = make([]float64, v)for j := range g.edges[i] {g.edges[i][j] = inf // 初始化为无穷大}}return g
}// AddEdge 添加边到图
func (g *Graph) AddEdge(u, v int, weight float64) {g.edges[u][v] = weight
}// FloydWarshall 实现 Floyd-Warshall 算法
func (g *Graph) FloydWarshall() [][]float64 {dist := make([][]float64, g.vertices)for i := range dist {dist[i] = make([]float64, g.vertices)copy(dist[i], g.edges[i])}for k := 0; k < g.vertices; k++ {for i := 0; i < g.vertices; i++ {for j := 0; j < g.vertices; j++ {if dist[i][k] != inf && dist[k][j] != inf {dist[i][j] = min(dist[i][j], dist[i][k]+dist[k][j])}}}}return dist
}// min 辅助函数,返回最小值
func min(a, b float64) float64 {if a < b {return a}return b
}func main() {g := NewGraph(4)g.AddEdge(0, 1, 3)g.AddEdge(1, 2, 4)g.AddEdge(2, 3, 2)g.AddEdge(0, 3, 10)g.AddEdge(3, 1, -6) // 负环边distances := g.FloydWarshall()for i := range distances {for j := range distances[i] {if distances[i][j] == inf {fmt.Print("∞ ")} else {fmt.Printf("%v ", distances[i][j])}}fmt.Println()}
}
说明
- 图的创建与边的添加部分如上实现,通过
FloydWarshall方法计算所有节点之间的最短路径,请注意可以增强打印自动识别达到∞的情况。该方法可以进一步调整,以融入更复杂的边权处理逻辑。
kimi:
要证明引理 24.10(三角不等式)可以处理最短路径权重为 ( \infty ) 和 ( -\infty ) 的情况,我们需要考虑这些特殊情况对不等式的影响。
引理 24.10(三角不等式)的一般形式
设 ( G = (V, E) ) 为一个带权重的有向图,其权重函数由 ( w: E \to \mathbb{R} ) 给出,其源结点为 ( s )。那么对于所有的边 ( (u, v) \in E ),我们有:
[ \delta(s, u) \leq \delta(s, u) + w(u, v) ]
特殊情况下的考虑
-
最短路径权重为 ( \infty ):
- 如果 ( \delta(s, u) = \infty ),那么不等式 ( \delta(s, u) \leq \delta(s, u) + w(u, v) ) 总是成立,因为 ( \infty + w(u, v) = \infty ) 对于任何实数 ( w(u, v) ) 都成立。
-
最短路径权重为 ( -\infty ):
- 如果 ( \delta(s, u) = -\infty ),那么不等式 ( \delta(s, u) \leq \delta(s, u) + w(u, v) ) 总是成立,因为 ( -\infty \leq -\infty + w(u, v) ) 对于任何实数 ( w(u, v) ) 都成立。
证明的改善
为了处理这些特殊情况,我们可以将引理 24.10 重新表述为:
[ \delta(s, u) \leq \delta(s, u) + w(u, v) ]
其中 ( \delta(s, u) ) 可以是任何实数,包括 ( \infty ) 和 ( -\infty )。
Go 语言实现
在 Go 语言中,我们可以使用 math.Inf 来表示 ( \infty ) 和 ( -\infty )。以下是如何在 Go 中实现这个不等式的示例:
package mainimport ("fmt""math"
)// 定义最短路径权重类型
type PathWeight float64// 检查三角不等式是否成立
func checkTriangleInequality(deltaSU, wUV PathWeight) bool {return deltaSU <= deltaSU + wUV
}func main() {// 示例权重deltaSU := PathWeight(math.Inf(1)) // 表示无穷大wUV := PathWeight(5)// 检查不等式if checkTriangleInequality(deltaSU, wUV) {fmt.Println("三角不等式成立:", deltaSU, "<=", deltaSU+wUV)} else {fmt.Println("三角不等式不成立")}// 示例权重deltaSU = PathWeight(math.Inf(-1)) // 表示负无穷大wUV = PathWeight(5)// 检查不等式if checkTriangleInequality(deltaSU, wUV) {fmt.Println("三角不等式成立:", deltaSU, "<=", deltaSU+wUV)} else {fmt.Println("三角不等式不成立")}
}
这段代码展示了如何在 Go 语言中处理最短路径权重为 ( \infty ) 和 ( -\infty ) 的情况,并验证三角不等式是否成立。
混元:
为了处理最短路径权重为 ∞ ∞ ∞ 和 − ∞ -∞ −∞ 的情况,我们需要对引理 24.10 的证明进行一些调整。具体来说,我们需要确保在计算最短路径时正确处理这些特殊情况。
以下是改进后的引理 24.10 的证明,并附带 Go 语言代码实现:
改进后的引理 24.10 证明
-
初始化:
- 设 δ ( s , s ) = 0 δ(s,s) = 0 δ(s,s)=0。
- 对于所有 v ∈ V v ∈ V v∈V 且 v ≠ s v ≠ s v=s,设 δ ( s , v ) = ∞ δ(s,v) = ∞ δ(s,v)=∞。
- 对于所有 v ∈ V v ∈ V v∈V,设 δ ( s , v ) = − ∞ δ(s,v) = -∞ δ(s,v)=−∞ 如果存在一条从 s s s 到 v v v 的路径,其权重为负无穷。
-
三角不等式:
- 对于所有的边 ( u , v ) ∈ E (u,v) ∈ E (u,v)∈E,我们需要证明 δ ( s , u ) ≤ δ ( s , u ) + w ( u , v ) δ(s,u) ≤ δ(s,u) + w(u,v) δ(s,u)≤δ(s,u)+w(u,v)。
-
处理特殊情况:
- 如果 δ ( s , u ) = ∞ δ(s,u) = ∞ δ(s,u)=∞ 或 w ( u , v ) = ∞ w(u,v) = ∞ w(u,v)=∞,则 δ ( s , u ) + w ( u , v ) = ∞ δ(s,u) + w(u,v) = ∞ δ(s,u)+w(u,v)=∞,显然 δ ( s , u ) ≤ ∞ δ(s,u) ≤ ∞ δ(s,u)≤∞。
- 如果 δ ( s , u ) = − ∞ δ(s,u) = -∞ δ(s,u)=−∞ 或 w ( u , v ) = − ∞ w(u,v) = -∞ w(u,v)=−∞,则 δ ( s , u ) + w ( u , v ) = − ∞ δ(s,u) + w(u,v) = -∞ δ(s,u)+w(u,v)=−∞,显然 δ ( s , u ) ≤ − ∞ δ(s,u) ≤ -∞ δ(s,u)≤−∞。
- 如果 δ ( s , u ) δ(s,u) δ(s,u) 和 w ( u , v ) w(u,v) w(u,v) 都是有限值,则直接应用三角不等式 δ ( s , u ) ≤ δ ( s , u ) + w ( u , v ) δ(s,u) ≤ δ(s,u) + w(u,v) δ(s,u)≤δ(s,u)+w(u,v)。
Go 语言代码实现
package mainimport ("fmt""math"
)const (inf = math.Inf(1)negInf = math.Inf(-1)
)type Edge struct {to intweight float64
}func shortestPath(graph [][]Edge, source int) []float64 {n := len(graph)dist := make([]float64, n)for i := range dist {if i == source {dist[i] = 0} else {dist[i] = inf}}for i := range graph {for _, edge := range graph[i] {if dist[i]+edge.weight < dist[edge.to] {dist[edge.to] = dist[i] + edge.weight}}}return dist
}func main() {graph := [][]Edge{{{to: 1, weight: 1}, {to: 2, weight: 4}},{{to: 2, weight: 2}, {to: 3, weight: 5}},{{to: 3, weight: 1}},{},}source := 0dist := shortestPath(graph, source)for i, d := range dist {if d == inf {fmt.Printf("Distance from %d to %d is ∞\n", source, i)} else if d == negInf {fmt.Printf("Distance from %d to %d is -∞\n", source, i)} else {fmt.Printf("Distance from %d to %d is %.2f\n", source, i, d)}}
}
解释
-
初始化:
dist数组初始化为 ∞ ∞ ∞,源节点的距离为 0 0 0。
-
更新距离:
- 使用 Bellman-Ford 算法更新每个节点的最短路径距离。
- 如果发现更短的路径,则更新距离。
-
处理特殊情况:
- 在输出结果时,检查距离是否为 ∞ ∞ ∞ 或 − ∞ -∞ −∞,并相应地输出。
通过这种方式,我们可以确保引理 24.10 的证明能够处理最短路径权重为 ∞ ∞ ∞ 和 − ∞ -∞ −∞ 的情况。
相关文章:

文心一言 VS 讯飞星火 VS chatgpt (383)-- 算法导论24.5 3题
三、对引理 24.10 的证明进行改善,使其可以处理最短路径权重为 ∞ ∞ ∞ 和 − ∞ -∞ −∞ 的情况。引理 24.10(三角不等式)的内容是:设 G ( V , E ) G(V,E) G(V,E) 为一个带权重的有向图,其权重函数由 w : E → R w:E→R w:E→R 给出&…...

【AIGC】如何通过ChatGPT轻松制作个性化GPTs应用
博客主页: [小ᶻZ࿆] 本文专栏: AIGC | GPTs应用实例 文章目录 💯前言💯什么是GPTsGPTs的工作原理GPTs的优势GPTs的应用前景总结 💯创建GPTS应用的基本流程进入GPTs创建界面方式一:按照引导完成生成创建GPTs方式二…...

gulp入门教程2:gulp发展历史
早期阶段(2013年-2014年) 诞生背景:随着前端开发复杂度的增加,开发者们开始寻求自动化工具来简化构建流程。2013年,由Fractal Innovations的Eric Schoffstall首次发布。它借鉴了Unix管道的流式处理思想,通…...

【实验八】前馈神经网络(4)优化问题
1 参数初始化 模型构建 模型训练 优化 完整代码 2 梯度消失问题 模型构建 模型训练 完整代码 3 死亡Relu问题 模型构建 模型训练 优化 完整代码 1 参数初始化 实现一个神经网络前,需要先初始化模型参数。如果对每一层的权重和偏置都用0初始化࿰…...

【深度学习】论文笔记:空间变换网络(Spatial Transformer Networks)
博主简介:努力学习的22级计算机科学与技术本科生一枚🌸博主主页: Yaoyao2024往期回顾: 【机器学习】有监督学习由浅入深讲解分类算法Fisher算法讲解每日一言🌼: 今天不想跑,所以才去跑,这才是长…...

Charles抓包_Android
1.下载地址 2.破解方法 3.安卓调试办法 查看官方文档,Android N之后抓包要声明App可用User目录下的CA证书 3.1.在Proxy下进行以下设置(路径Proxy->Proxy Settings) 3.1.1.不抓包Windows,即不勾选此项,免得打输出不…...
【MATLAB源码-第204期】基于matlab的语音降噪算法对比仿真,谱减法、维纳滤波法、自适应滤波法;参数可调。
操作环境: MATLAB 2022a 1、算法描述 语音降噪技术的目的是改善语音信号的质量,通过减少或消除背景噪声,使得语音更清晰,便于听者理解或进一步的语音处理任务,如语音识别和语音通讯。在许多实际应用中,如…...

Scala的包及其导入
//1.单个导入 //import com.sala02.A //import com.sala02.B //2.导入多个类 //import com.sala02.{A,B} //3.导入一个包下的所有类:包名._ //import com.sala02._ //4.导入一个包中的类,给他改个名字 //格式:import 包名.{原来的名字 > 新…...

deepfm模型实现招聘职位推荐算法
项目源码获取方式见文章末尾! 600多个深度学习项目资料,快来加入社群一起学习吧。 《------往期经典推荐------》 项目名称 1.【基于CNN-RNN的影像报告生成】 2.【卫星图像道路检测DeepLabV3Plus模型】 3.【GAN模型实现二次元头像生成】 4.【CNN模型实现…...

编程之路:蓝桥杯备赛指南
文章目录 一、蓝桥杯的起源与发展二、比赛的目的与意义三、比赛内容与形式四、比赛前的准备五、获奖与激励六、蓝桥杯的影响力七、蓝桥杯比赛注意事项详解使用Dev-C的注意事项 一、蓝桥杯的起源与发展 蓝桥杯全国软件和信息技术专业人才大赛,简称蓝桥杯,…...

Android 15 在状态栏时间中显示秒数
这是更新后的博客草稿,关于在Android 15状态栏中显示秒数的实现: 在Android 15状态栏中显示秒数 在Android 15中,您可以通过两种方式在状态栏中显示秒数:使用ADB命令或修改系统源代码。下面详细介绍这两种方法。 方法一:通过ADB实现 您可以使用ADB(Android调试桥)命令…...

Flutter 鸿蒙next版本:自定义对话框与表单验证的动态反馈与错误处理
在现代移动应用开发中,用户体验是至关重要的一环。Flutter和鸿蒙操作系统(HarmonyOS)的结合,为开发者提供了一个强大的平台,以创建跨平台、高性能的应用程序。本文将探讨如何在Flutter与鸿蒙next版本中创建自定义对话框…...

Unreal Engine5中使用 Lyra框架
UE5系列文章目录 文章目录 UE5系列文章目录前言一、Lyra和AIS框架的区别二、下载官方Lyra游戏示例三、Lyra在动画蓝图中的使用 前言 Unreal Engine 5(UE5)提供了多种用于游戏开发的模板和框架,其中Lyra和AlS是两个不同的示例项目,…...

Spring Security-02-Spring Security认证方式-HTTP基本认证、Form表单认证、HTTP摘要认证、前后端分离安全处理方案
Lison <dreamlison163.com>, v1.0.0, 2024.06.01 Spring Security-02-Spring Security认证方式-HTTP基本认证、Form表单认证、HTTP摘要认证、前后端分离安全处理方案 文章目录 Spring Security-02-Spring Security认证方式-HTTP基本认证、Form表单认证、HTTP摘要认证、…...

【scikit-learn 1.2版本后】sklearn.datasets中load_boston报错 使用 fetch_openml 函数来加载波士顿房价
ImportError: load_boston has been removed from scikit-learn since version 1.2. 由于 load_boston 已经在 scikit-learn 1.2 版本中被移除,需要使用 fetch_openml 函数来加载波士顿房价数据集。 # 导入sklearn数据集模块 from sklearn import datasets # 导入波…...

vxe-table v4.8+ 与 v3.10+ 导出 xlsx、支持导出合并、设置样式、宽高、边框、字体、背景、超链接、图片的详细介绍,一篇就够了
Vxe UI vue vxe-table v4.8 与 v3.10 导出 xlsx、支持导出合并、设置样式、宽高、边框、字体、背景、超链接、图片等、所有常用的 Excel 格式都能自定义,使用非常简单,纯前端实现复杂的导出。 安装插件 npm install vxe-pc-ui4.2.39 vxe-table4.8.0 vx…...

江协科技STM32学习- P36 SPI通信外设
🚀write in front🚀 🔎大家好,我是黄桃罐头,希望你看完之后,能对你有所帮助,不足请指正!共同学习交流 🎁欢迎各位→点赞👍 收藏⭐️ 留言📝…...

【大数据】ClickHouse常见的表引擎及建表语法
ClickHouse 中最强大的表引擎当属 MergeTree (合并树)引擎及该系列(*MergeTree)中的其他引擎。接下来我们就仔细了解下MergeTree 及该系列的其他引擎的使用场景及建表语法。 MergeTree MergeTree 系列的引擎被设计用于插入极大量…...

explain执行计划分析 ref_
这里写目录标题 什么是ExplainExplain命令扩展explain extendedexplain partitions 两点重要提示本文示例使用的数据库表Explain命令(关键字)explain简单示例explain结果列说明【id列】【select_type列】【table列】【type列】 【possible_keys列】【key列】【key_len列】【ref…...

网络学习/复习4传输层
1,0...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...

【51单片机】4. 模块化编程与LCD1602Debug
1. 什么是模块化编程 传统编程会将所有函数放在main.c中,如果使用的模块多,一个文件内会有很多代码,不利于组织和管理 模块化编程则是将各个模块的代码放在不同的.c文件里,在.h文件里提供外部可调用函数声明,其他.c文…...
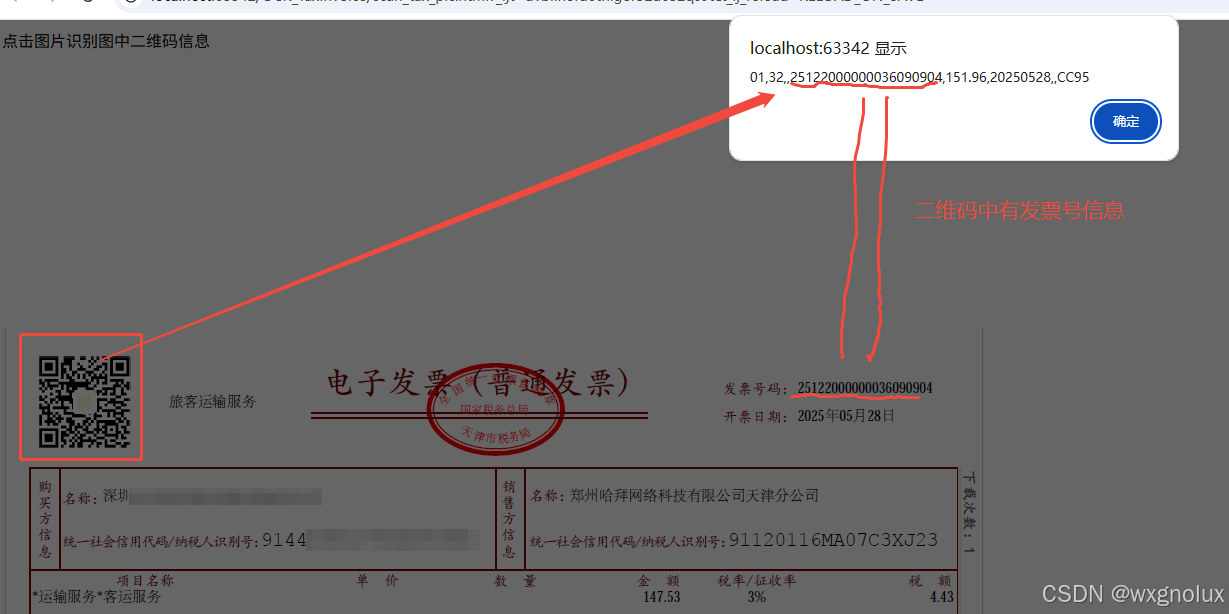
网页端 js 读取发票里的二维码信息(图片和PDF格式)
起因 为了实现在报销流程中,发票不能重用的限制,发票上传后,希望能读出发票号,并记录发票号已用,下次不再可用于报销。 基于上面的需求,研究了OCR 的方式和读PDF的方式,实际是可行的ÿ…...
数据挖掘是什么?数据挖掘技术有哪些?
目录 一、数据挖掘是什么 二、常见的数据挖掘技术 1. 关联规则挖掘 2. 分类算法 3. 聚类分析 4. 回归分析 三、数据挖掘的应用领域 1. 商业领域 2. 医疗领域 3. 金融领域 4. 其他领域 四、数据挖掘面临的挑战和未来趋势 1. 面临的挑战 2. 未来趋势 五、总结 数据…...
