vue3动态监听div高度案例
案例场景

场景描述:现在左边的线条长度需要根据右边盒子的高度进行动态变化
实践代码案例
HTML部分
<div v-for="(device, index) in devices" :key="index"><!-- 动态设置 .left-bar 的高度 --><div class="left-bar" :style="{ height: `${contentHeights[index] || 30}px` }"></div><div :ref="(el) => { contentRefs[index] = el as HTMLElement }"><span>设备编号:{{ device.code }}</span><span>异常信息:{{ device.info }}</span></div>
</div>
JS部分
import { reactive, toRefs, ref, onMounted, watch, nextTick } from 'vue';interface Device {code: string;status: string;info: string;
}const state = reactive({devices:[{code: 'JS23053001',status: '异常',info: '提升激光仪通讯故障 提升激光仪通讯故障 备用(从站数据故障) 备用(从站数据故障)'},{code: 'JS23053002',status: '异常',info: '货物左超 过载保护 断绳保护 超速保护 行走超限 升降超限'},{ code: 'JS23053003', status: '正常', info: '正常' },{ code: 'JS23053003', status: '正常', info: '正常' },{code: 'JS23053003',status: '异常',info: '行走变频器通讯故障 行走变频器通讯故障 货叉1变频器通讯故障'}],
});const { devices } = toRefs(state);// 用于存储每个 content 元素的引用
const contentRefs = ref<(HTMLElement | null)[]>([]);// 存储每个设备的 .content 元素的高度
const contentHeights = ref<number[]>([]);// 更新每个设备的 content 高度
const updateContentHeight = () => {
contentHeights.value = contentRefs.value.map(contentRef => {// 获取每个 content 元素的高度return contentRef ? contentRef.clientHeight : 0;});
};// 监听设备列表变化,重新更新高度
watch(() => state.devices, () => {nextTick(() => updateContentHeight()); // 确保 DOM 渲染完成后获取高度
}, { immediate: true });
Style部分(left-bar)
.device-item .left-bar {width: 2px; // 宽度margin-right: 0.2rem; // 距离
}
注意:
- 使用 nextTick 确保 DOM 渲染完成后再更新 contentHeights。这能保证获取到准确的高度信息
- 给 .left-bar 设置一个默认高度(例如 30px)来确保它始终可见,即使计算出来的高度是 0 时。你可以调试默认高度,并逐步确保 contentHeights 数组能够正常更新
- contentRefs 是一个数组,用来存储每个 .content 的引用。由于 v-for 渲染的组件是异步的,可能 contentRefs 没有及时更新,导致没有正确获取到每个 .content 的高度
相关文章:

vue3动态监听div高度案例
案例场景 场景描述:现在左边的线条长度需要根据右边盒子的高度进行动态变化 实践代码案例 HTML部分 <div v-for"(device, index) in devices" :key"index"><!-- 动态设置 .left-bar 的高度 --><div class"left-bar"…...

数据转换 | Matlab基于SP符号递归图(Symbolic recurrence plots)一维数据转二维图像方法
目录 基本介绍程序设计参考资料获取方式 基本介绍 Matlab基于SP符号递归图(Symbolic recurrence plots)一维数据转二维图像方法 符号递归图(Symbolic recurrence plots)是一种一维时间序列转图像的技术,可用于平稳和非平稳数据集;对噪声具有…...

分类算法——逻辑回归 详解
逻辑回归(Logistic Regression)是一种广泛使用的分类算法,特别适用于二分类问题。尽管名字中有“回归”二字,逻辑回归实际上是一种分类方法。下面将从底层原理、数学模型、优化方法以及源代码层面详细解析逻辑回归。 1. 基本原理 …...

只允许指定ip远程连接ssh
我们都会使用securtcrt或者xshell等软件进行远程登录,这样虽然会给我们带来很多便捷,但是同样会存在一定的风险。有很多人专门通过重复的扫描试图破解我们的linux服务器,从而获取免费的“肉鸡”。因此我们可以通过设置hosts.allow和hosts.den…...

Rust 力扣 - 2841. 几乎唯一子数组的最大和
文章目录 题目描述题解思路题解代码题目链接 题目描述 题解思路 我们遍历长度为k的窗口,用一个哈希表记录窗口内的所有元素(用来对窗口内元素去重),我们取哈希表中元素数量大于等于m的窗口总和的最大值 题解代码 use std::coll…...

TwinCL: A Twin Graph Contrastive Learning Model for Collaborative Filtering
TwinCL: A Twin Graph Contrastive Learning Model for Collaborative Filtering 摘要 在推荐和协同过滤领域,图对比学习(Graph Contrasive Learning,GCL)已经成为一种有影响的方法。然而,对比学习有效性的原因还没有…...
如何区分实例化网格中的每个实例
1)如何区分实例化网格中的每个实例 2)项目在模拟器上切换程序后有概率画面冻结 3)Unity工程导入团结引擎,GUID会变化,导致引用关系丢失 4)Mask在Android平台下渲染异常 这是第407篇UWA技术知识分享的推送&a…...

理解 WordPress | 第一篇:与内容管理系统的关系
初步了解 WordPress 在互联网世界里,WordPress 是一个家喻户晓的名字。它是一个开源的内容管理系统(Content Management System,简称 CMS),帮助用户轻松创建和管理网站。WordPress 诞生于 2003 年,最初是一…...

Python游戏脚本之实现飞机大战(附源码)
一.游戏设定 游戏界面如下图所示: 游戏的基本设定: 敌方共有大中小3款飞机,分为高中低三种速度; 子弹的射程并非全屏,而大概是屏幕长度的80%; 消灭小飞机需要1发子弹,中飞机需要8发,大飞机需要20发子弹; 每消灭一架小飞机得1000分,中飞机6000分,大飞…...

使用Spring Boot搭建简单的web服务
1 引言 1.1 Spring Boot简介 Spring Boot是由Pivotal团队提供的一套开源框架,旨在简化Spring应用的创建及部署。 一、核心设计思想 Spring Boot的核心设计思想是“约定优于配置”(Convention Over Configuration,简称COC)。这…...

【IF-MMIN】利用模态不变性特征进行缺失模态的鲁棒多模态情感识别
代码地址:github地址传送 文章是基于MMIN的改进 -> MMIN传送 abstract 多模态情感识别利用跨模态的互补信息来获得性能。然而,我们不能保证所有模式的数据总是存在于实践中。在跨模态数据缺失预测研究中,异质性模态之间的固有差异即模态…...

RGB图像,排列方式NHWC适合CPU计算,NCHW适合GPU计算
之前写过笔记OpenCV读取图像时按照BGR的顺序HWC排列,PyTorch按照RGB的顺序CHW排列,HWC格式排列,那么内存位置计算公式是? 在比较NHWC(channels_last)和NCHW(channels_first)这两种图像数据通道格式的效率时…...

布朗运动
内容来源 数理金融初步(原书第3版)Sheldon M. Ross著 冉启康译 机械工业出版社 布朗运动 定义 如果随机变量集合 X ( t ) X(t) X(t) 满足以下条件 X ( 0 ) X(0) X(0) 是一个给定的常数 对所有正数 y y y 和 t t t,随机变量 X ( y t …...

WPF+MVVM案例实战(二十二)- 制作一个侧边弹窗栏(CD类)
文章目录 1、案例效果1、侧边栏分类2、CD类侧边弹窗实现1、样式代码实现2、功能代码实现3 运行效果4、源代码获取1、案例效果 1、侧边栏分类 A类 :左侧弹出侧边栏B类 :右侧弹出侧边栏C类 :顶部弹出侧边栏D类 :底部弹出侧边栏2、CD类侧边弹窗实现 1、样式代码实现 在原有的…...
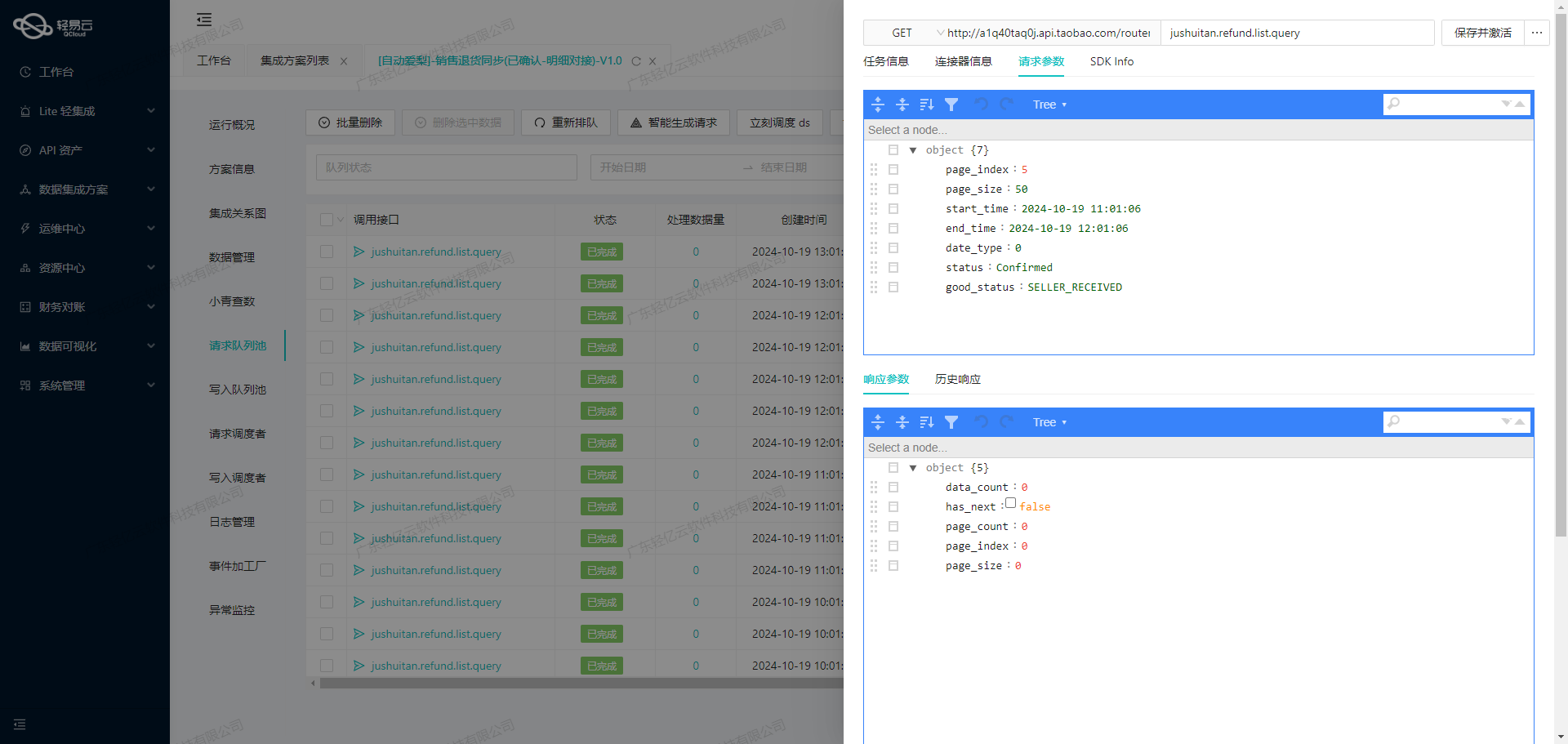
集成旺店通旗舰版售后单至MySQL数据库
旺店通旗舰版-售后单集成到MySQL的技术实现 在数据驱动的业务环境中,如何高效、准确地将旺店通旗舰奇门的数据集成到MySQL数据库,是许多企业面临的重要挑战。本文将分享一个具体的系统对接案例:旺店通旗舰版-售后单-->BI泰海-售后订单表(…...

【Linux】从零开始使用多路转接IO --- epoll
当你偶尔发现语言变得无力时, 不妨安静下来, 让沉默替你发声。 --- 里则林 --- 从零开始认识多路转接 1 epoll的作用和定位2 epoll 的接口3 epoll工作原理4 实现epollserverV1 1 epoll的作用和定位 之前提过的多路转接方案select和poll 都有致命缺点…...

爬虫学习4
from threading import Thread#创建任务 def func(name):for i in range(100):print(name,i)if __name__ __main__:#创建线程t1 Thread(targetfunc,args("1"))t2 Thread(targetfunc, args("2"))t1.start()t2.start()print("我是诛仙剑")from …...
CTF之web题集详情随手笔记
《Web安全》http://mp.weixin.qq.com/s?__bizMzkwNjY1Mzc0Nw&mid2247484238&idx1&snca66551c31e37b8d726f151265fc9211&chksmc0e47a12f793f3049fefde6e9ebe9ec4e2c7626b8594511bd314783719c216bd9929962a71e6&scene21#wechat_redirect 1 WEB 1 靶场目…...

TDengine 集群能力:超越 InfluxDB 的水平扩展与开源优势
随着物联网、车联网等领域的快速发展,企业所面临的数据采集量呈爆炸式增长,这对 IT 基础设施和数据库提出了严峻挑战。传统单机版数据库逐渐无法应对高并发的数据写入和复杂的查询需求。因此,底层数据库必须具备水平扩展能力,以确…...

MATCH_DIRECT_BOOT_AWARE和MATCH_DIRECT_BOOT_UNAWARE
PackageManager.MATCH_DIRECT_BOOT_AWARE和PackageManager.MATCH_DIRECT_BOOT_UNAWARE 在Android系统中,PackageManager类提供了一些标志位,用于控制查询系统中的应用和组件时的行为。其中,MATCH_DIRECT_BOOT_AWARE和MATCH_DIRECT_BOOT_UNAWA…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...

土建施工员考试:建筑施工技术重点知识有哪些?
《管理实务》是土建施工员考试中侧重实操应用与管理能力的科目,核心考查施工组织、质量安全、进度成本等现场管理要点。以下是结合考试大纲与高频考点整理的重点内容,附学习方向和应试技巧: 一、施工组织与进度管理 核心目标: 规…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...
