【贝叶斯公式】贝叶斯公式、贝叶斯定理、贝叶斯因子,似然比
一、是什么?
贝叶斯公式的本质在于它提供了一种在已有知识的基础上更新和调整我们对事件的信念的方式。具体来说,贝叶斯公式描述了后验概率(即在观察到某些证据后更新的概率)与先验概率(即在没有观察证据之前的概率)以及似然性(即在给定某种假设条件下观察到证据的概率)之间的关系。
贝叶斯公式可以表示为:

其中:
P(A∣B) 是后验概率,即在事件 B 发生后,事件 A 发生的概率。
P(A) 是先验概率,即在观察到事件 B 之前,事件 A 发生的概率。
P(B∣A) 是似然概率,即在事件 A 发生的条件下,事件 B 发生的概率;本质是新获得的信息对事件的支持度。
P(B) 是边际概率,即事件 B 发生的总概率。
本质:
贝叶斯公式的核心在于知识的更新。它允许我们基于新获得的信息(证据)对我们的信念进行调整,反映出在观察到证据后对不确定性的减少。先验概率反映了我们在观察数据之前的信念,而后验概率则是结合了数据后更新的信念。这种转变体现了如何利用已有的信息进行推理。
二、例子
例子来源:3BlueBrown的视频
【官方双语】贝叶斯定理,使概率论直觉化_哔哩哔哩_bilibili![]() https://www.bilibili.com/video/BV1R7411a76r/?spm_id_from=333.1391.0.0&vd_source=ecbdfcacb078d0e3626e61248866cdc7
https://www.bilibili.com/video/BV1R7411a76r/?spm_id_from=333.1391.0.0&vd_source=ecbdfcacb078d0e3626e61248866cdc7
Steve是一个温顺而又井井有条的人,那么他会是一个图书馆管理员还是一位农民呢?
通过性格,图书馆管理员符合条件的有,而他是农民的概率是
。(似然概率)
他是图书馆管理员的可能性就一定大吗?
在现实世界中图书馆管理员和农民的数量比为1:20,所以现实中的图书馆管理员是,农民是
,(先验概率)
那么他是图书馆管理员的概率为:
本质
如果没有性格的信息,以我们的基础知识,我们认为他是图书馆管理员的概率为
加上性格信息
随后我们原先的认知改变为
即认知由更新为
也可以由图形来理解:
如下图,先验概率为,即现实世界中图书馆管理员与农民的数量比为1:20


图书管理员中性格符合的有,农民中性格符合的有

所要求的
三、从比率角度理解贝叶斯公式
理论来源:
【官方双语】医检阳性≠得了病?重新理解贝叶斯定理_哔哩哔哩_bilibili![]() https://www.bilibili.com/video/BV1Ei4y1F72M/?spm_id_from=333.1391.0.0&vd_source=ecbdfcacb078d0e3626e61248866cdc7
https://www.bilibili.com/video/BV1Ei4y1F72M/?spm_id_from=333.1391.0.0&vd_source=ecbdfcacb078d0e3626e61248866cdc7
3.1贝叶斯因子
(1)贝叶斯因子
在《二》中的例子中,贝叶斯因子为
(2)在《二》中的例子中写成比率的形式,先验为1:20,后验为4:20,显然比率扩大了4倍,贝叶斯因子为4,所以
后验比率=先验比率×贝叶斯因子
理解:在通过上面这个比率公式来理解贝叶斯公式时,更加符合直觉,还有一个好处是,即时改变了先验,也能很快地计算后验,因为这里地贝叶斯因子只与新获得的信息有关,而与先验无关,先验改变时,贝叶斯因子不改变。
3.2贝叶斯因子与似然比
(1)贝叶斯因子与似然比
似然比,即似然概率的比值。它的本质在于它衡量了新获得的信息对两种假设的相对支持度,它不同于概率(即单一假设下事件发生的可能性),而是关注两个假设下数据出现的可能性对比。
本文中的贝叶斯因子即为似然比,在上述例子中新获得的信息是“性格温顺且井井有条”,其对“是图书馆管理员”的支持度为:,对“是农民”的支持度为:
。似然比为
,

(2)似然比定义:

(3)似然比定义解读

(4)似然比在诊断测试中的应用

相关文章:

【贝叶斯公式】贝叶斯公式、贝叶斯定理、贝叶斯因子,似然比
一、是什么? 贝叶斯公式的本质在于它提供了一种在已有知识的基础上更新和调整我们对事件的信念的方式。具体来说,贝叶斯公式描述了后验概率(即在观察到某些证据后更新的概率)与先验概率(即在没有观察证据之前的概率&a…...

[libos源码学习 1] Liboc协程生产者消费者举例
文章目录 1. CoRoutineEnv_t结构体用于管理协程环境 3 Liboc协程生产者消费者例子4 Liboc协程生产者消费者, 为什么队列不需要上锁?5. 两个协程访问资源不需要加队列吗5. 参考 1. CoRoutineEnv_t结构体用于管理协程环境 struct stCoRoutineEnv_t { stCo…...

Python OpenCV 图像改变
更改图像数据 通过 改像素点 或者 切片的区域 import cv2 import numpy as np img cv2.imread("image.jpg") print(img[3,5]) # 显示某位置(行3列5)的像素值( 如 [53 34 29] 它是有三通道 B G R 组成) img[3,5] (0,0,255) # 更改该位置的像素…...

k8s按需创建 PV和创建与使用 PVC
在 Kubernetes 中,PersistentVolume(PV)和 PersistentVolumeClaim(PVC)用于管理存储资源。PV 是集群中的存储资源,而 PVC 是 Pod 请求 PV 的方式。按需创建 PV 通常使用 StorageClass 实现动态存储分配&…...
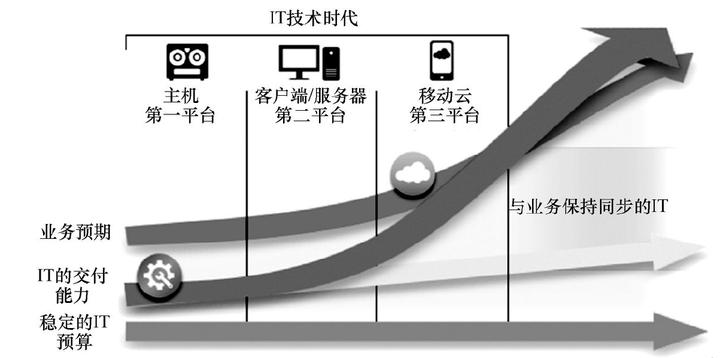
揭秘云计算 | 2、业务需求推动IT发展
揭秘云计算 | 1、云从哪里来?-CSDN博客https://blog.csdn.net/Ultipa/article/details/143430941?spm1001.2014.3001.5502 书接上文: 过去几十年间IT行业从大型主机过渡到客户端/服务器,再过渡到现如今的万物互联,IT可把控的资…...

【系统面试篇】进程与线程类(2)(笔记)——进程调度、中断、异常、用户态、核心态
目录 一、相关面试题 1. 进程的调度算法有哪些? 调度原则 (1)先来先服务调度算法 (2)最短作业优先调度算法 (3)高响应比优先调度算法 (4)时间片轮转调度算法 &am…...

基于MySQL的企业专利数据高效查询与统计实现
背景 在进行产业链/产业评估工作时,我们需要对企业的专利进行评估,其中一个重要指标是统计企业每一年的专利数量。本文基于MySQL数据库,通过公司名称查询该公司每年的专利数,实现了高效的专利数据统计。 流程 项目流程概述如下&…...

热成像手机VS传统热成像仪:AORO A23为何更胜一筹?
热成像技术作为一种非接触式测温方法,广泛应用于石油化工巡检、电力巡检、应急救援、医疗、安防等“危、急、特”场景。提及热成像设备,人们往往会首先想到价格高昂、操作复杂且便携性有限的热成像仪。但是,随着技术的不断进步,市…...

Spring IoC——依赖注入
1. 依赖注入的介绍 DI,也就是依赖注入,在容器中建立的 bean (对象)与 bean 之间是有依赖关系的,如果直接把对象存在 IoC 容器中,那么就都是一个独立的对象,通过建立他们的依赖关系,…...

Linux 中,flock 对文件加锁
在Linux中,flock是一个用于对文件加锁的实用程序,它可以帮助协调多个进程对同一个文件的访问,避免出现数据不一致或冲突等问题。以下是对flock的详细介绍: 基本原理 flock通过在文件上设置锁来控制多个进程对该文件的并发访问。…...
CentOS下载ISO镜像的方法
步骤 1:访问CentOS官方网站 首先,打开浏览器,输入CentOS的官方网站地址:Download 在网站上找到ISO镜像的下载链接,通常位于“Downloads”或类似的页面上。 选择所需的CentOS版本和架构(如x86_64…...

Node.js 入门指南:从零开始构建全栈应用
🌈个人主页:前端青山 🔥系列专栏:node.js篇 🔖人终将被年少不可得之物困其一生 依旧青山,本期给大家带来node.js篇专栏内容:node.js-入门指南:从零开始构建全栈应用 前言 大家好,我是青山。作…...

MYSQL 真实高并发下的死锁
https://pan.baidu.com/s/1nM3VQdbkNZhnK-wWboEYxA?pwdvwu6 下面是风控更新语句 ------------------------ LATEST DETECTED DEADLOCK ------------------------ 2023-08-04 01:00:10 140188779017984 *** (1) TRANSACTION: TRANSACTION 895271870, ACTIVE 0 sec starting …...

Zookeeper 简介 | 特点 | 数据存储
1、简介 zk就是一个分布式文件系统,不过存储数据的量极小。 1. zookeeper是一个为分布式应用程序提供的一个分布式开源协调服务框架。是Google的Chubby的一个开源实现,是Hadoop和Hbase的重要组件。主要用于解决分布式集群中应用系统的一致性问题。 2. 提…...

设计模式之结构型模式---装饰器模式
目录 1.概述2.类图3.应用场景及优缺点3.1 应用场景3.2 优缺点3.2.1 优点3.2.2 缺点 4.实现4.1 案例类图4.2 代码实现4.2.1 定义抽象构建角色4.2.2 定义具体构建角色4.2.3 定义抽象装饰器角色4.2.4 定义具体装饰角色4.2.5 装饰器模式的使用 1.概述 装饰器模式是指在不改变现有对…...

Android Pair
Pair在Android中是一种轻量级的工具类,并不是严格意义上的数据结构。 数据结构是一组有组织的方式来存储和管理数据的方式,如数组、链表、栈、队列、树、图等,它们有自己的特性和操作规则。而Pair更像是一个简单的封装,用于在需要…...

华为荣耀曲面屏手机下面空白部分设置颜色的方法
荣耀部分机型下面有一块空白区域,如下图红框部分 设置这部分的颜色需要在themes.xml里面设置navigationBarColor属性 <item name"android:navigationBarColor">android:color/white</item>...

《C#语法一篇通》,有20万字,需8MB字节,宜48小时阅读,没准会继续完善
本文摘录了C#语法的主要内容,接近20万字。 所有鸡汤的味道都等于马尿! 如果你相信任何所谓的鸡汤文章,智商堪忧。 计算机语言没有”好不好“之说,骗子才会告诉你哪个语言好,学好任何一本基础语言(C&#…...

嵌入式硬件工程师的职业发展规划
嵌入式硬件工程师可以按照以下阶段进行职业发展规划: 1. **初级阶段(1-3 年) ** - **技术学习与积累**: **电路基础强化**: 深入学习模拟电路和数字电路知识,能够熟练分析和设计基本的电路,…...

QT for android 问题总结(QT 5.15.2)
1.配置好的sdk,显示设置失败 Android SDK Command-line Tools run. Android Platform-Tools installed. Command-line Tools (latest) 版本过高导致报错 ,下载一个低版本的latest ,替换掉之前latest中的文件。即可,latest 路径如…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...
