非线性数据结构之图

一、有向图（Directed Graph）

1. 定义

有向图是一个由顶点（节点）和有方向的边（弧）组成的图。在有向图中，每条边都有一个起点和一个终点，表示从一个顶点到另一个顶点的关系。

2. 特点

• 边有方向：每条边都有一个方向，通常用箭头表示。例如，边 A→B 表示从顶点 A 到顶点 B。
• 可能存在孤立点：有向图中的某些顶点可能没有入边或出边。
• 可有多个入度和出度：顶点的入度是指指向该顶点的边数，出度是指从该顶点出发的边数。

3. 优缺点

• 优点：

  • 能够准确表示有向关系，如网页链接、任务调度等。
  • 适合表示不对称的关系。

• 缺点：

  • 复杂性较高，特别是在涉及遍历和路径寻找时。
  • 算法实现相对复杂，如最短路径算法。

4. 应用场景

• 网络路由：表示计算机网络中的连接。
• 任务调度：表示任务之间的依赖关系。
• 图形界面：表示用户界面元素之间的交互。

5. 示例

有向图可以用邻接表或邻接矩阵表示。以下是一个有向图的示例：

示例代码（Java 实现）

import java.util.*;class DirectedGraph {private Map<String, List<String>> adjacencyList;public DirectedGraph() {adjacencyList = new HashMap<>();}public void addVertex(String vertex) {adjacencyList.putIfAbsent(vertex, new ArrayList<>());}public void addEdge(String from, String to) {adjacencyList.putIfAbsent(from, new ArrayList<>());adjacencyList.putIfAbsent(to, new ArrayList<>());adjacencyList.get(from).add(to);}public List<String> getNeighbors(String vertex) {return adjacencyList.get(vertex);}
}

二、无向图（Undirected Graph）

1. 定义

无向图是一个由顶点和无方向的边组成的图。在无向图中，边连接两个顶点，但没有方向。

2. 特点

• 边无方向：边表示的是两个顶点之间的关系，通常用线段表示。例如，边 A−B 表示顶点 A 和顶点 B 是相连的。
• 每条边相互对称：如果存在边 A−B，则同时存在边 B−A。
• 所有顶点具有相同的边关系。

3. 优缺点

• 优点：

  • 适合表示对称关系，如社交网络、朋友关系。
  • 较简单的算法实现。

• 缺点：

  • 对于某些应用，缺乏表达方向性的能力。
  • 在某些情况下，图的结构可能会显得过于简单。

4. 应用场景

• 社交网络：表示用户之间的朋友关系。
• 电路设计：表示电路中元件之间的连接。
• 城市交通：表示城市道路网络。

5. 示例

无向图可以用邻接表或邻接矩阵表示。以下是一个无向图的示例：

示例代码（Java 实现）

import java.util.*;class UndirectedGraph {private Map<String, List<String>> adjacencyList;public UndirectedGraph() {adjacencyList = new HashMap<>();}public void addVertex(String vertex) {adjacencyList.putIfAbsent(vertex, new ArrayList<>());}public void addEdge(String vertex1, String vertex2) {adjacencyList.putIfAbsent(vertex1, new ArrayList<>());adjacencyList.putIfAbsent(vertex2, new ArrayList<>());adjacencyList.get(vertex1).add(vertex2);adjacencyList.get(vertex2).add(vertex1); // 无向边}public List<String> getNeighbors(String vertex) {return adjacencyList.get(vertex);}
}

三、加权图（Weighted Graph）

1. 定义

加权图是一个图，其中每条边都分配有一个权重（或成本）。权重可以表示距离、时间、费用等多种含义。

2. 特点

• 每条边有权重：边的权重通常是一个数值，表示从一个顶点到另一个顶点的代价。
• 支持最短路径计算：适合用于计算从一个顶点到另一个顶点的最短路径。
• 可以是有向或无向图：加权图可以是有向的或无向的。

3. 优缺点

• 优点：

  • 能够表示复杂的关系，如交通网络、物流等。
  • 可以使用多种算法（如 Dijkstra、Bellman-Ford）进行路径优化。

• 缺点：

  • 处理复杂性较高，尤其是在大量边和顶点的情况下。
  • 可能导致计算错误，尤其在负权重情况下（如 Bellman-Ford 算法）。

4. 应用场景

• 地图导航：用于计算从起点到终点的最短路径。
• 网络流量：分析和优化网络数据传输。
• 电路分析：计算电路中元件之间的电流和电压。

5. 示例

加权图的表示通常使用邻接表或邻接矩阵。以下是一个加权图的示例：

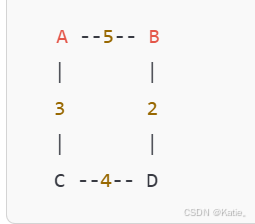
示例代码（Java 实现）

import java.util.*;class WeightedGraph {private Map<String, List<Edge>> adjacencyList;class Edge {String destination;int weight;Edge(String destination, int weight) {this.destination = destination;this.weight = weight;}}public WeightedGraph() {adjacencyList = new HashMap<>();}public void addVertex(String vertex) {adjacencyList.putIfAbsent(vertex, new ArrayList<>());}public void addEdge(String from, String to, int weight) {adjacencyList.putIfAbsent(from, new ArrayList<>());adjacencyList.putIfAbsent(to, new ArrayList<>());adjacencyList.get(from).add(new Edge(to, weight));adjacencyList.get(to).add(new Edge(from, weight)); // 如果是无向图}public List<Edge> getNeighbors(String vertex) {return adjacencyList.get(vertex);}
}

总结比较

图类型	边的方向性	权重	适用场景
有向图	有方向	无	任务调度、网络路由
无向图	无方向	无	社交网络、城市交通
加权图	有向/无向	有	地图导航、网络流量、电路分析

通过这些详细的介绍，可以更清晰地理解不同图类型的特点和应用场景，为具体问题的解决选择合适的数据结构提供帮助。