pytorch学习:矩阵分解:奇异值分解(SVD分解)
前言
矩阵分解(Matrix Decomposition)是将一个矩阵分解成多个矩阵的乘积的过程,这种分解方法在计算、机器学习和线性代数中有广泛应用。不同的分解方式可以简化计算、揭示矩阵的内在结构或提高算法的效率。
奇异值分解
奇异值分解(Singular Value Decomposition, SVD)是矩阵分解的一种重要形式,它将一个任意的矩阵分解为三个矩阵的乘积,从而揭示出原矩阵的内在结构。
对于任意一个m×n 的矩阵A,它的奇异值分解可以表示为:
其中:
U 是一个 m×m 的正交矩阵,称为左奇异向量矩阵。
V 是一个 n×n 的正交矩阵,称为右奇异向量矩阵。
Σ 是一个 m×n 的对角矩阵,其中对角线上的元素是矩阵 A 的奇异值,其余元素为零。奇异值是非负实数,按降序排列,即 σ 1≥σ 2 ≥⋯≥σ r≥0,其中σ r 是方阵的秩的根号值。
注:正交矩阵(Orthogonal Matrix)是指一种特殊的方阵,一个 n×n 的矩阵 Q 被称为正交矩阵,如果它满足Q TQ=QQ T =I其中Q T是 Q 的转置矩阵,I 是n×n 的单位矩阵。
求解步骤:
1.求矩阵。
2.求矩阵的特征值和特征向量(正交化)。
3.求奇异值(特征值开方)和正交矩阵。
4.求正交矩阵U。
实例
1.方阵的分解


代码实现:
import torcha = torch.Tensor([[3,1],[1,3]])
u,s,v = torch.svd(a)
print(a)
print(u)
print(s)
print(v)
print(torch.svd(a))运行结果:
tensor([[3., 1.],[1., 3.]])
tensor([[-0.7071, -0.7071],[-0.7071, 0.7071]])
tensor([4., 2.])
tensor([[-0.7071, -0.7071],[-0.7071, 0.7071]])
torch.return_types.svd(
U=tensor([[-0.7071, -0.7071],[-0.7071, 0.7071]]),
S=tensor([4., 2.]),
V=tensor([[-0.7071, -0.7071],[-0.7071, 0.7071]]))2.矩形阵的分解


代码实现:
import torcha = torch.Tensor([[4,0],[3,0],[0,5]])
u,s,v = torch.svd(a)
print(a)
print(u)
print(s)
print(v)
print(torch.svd(a))
运行结果:
tensor([[4., 0.],[3., 0.],[0., 5.]])
tensor([[-0.8000, 0.0000],[-0.6000, 0.0000],[ 0.0000, -1.0000]])
tensor([5., 5.])
tensor([[-1., -0.],[-0., -1.]])
torch.return_types.svd(
U=tensor([[-0.8000, 0.0000],[-0.6000, 0.0000],[ 0.0000, -1.0000]]),
S=tensor([5., 5.]),
V=tensor([[-1., -0.],[-0., -1.]]))相关文章:

pytorch学习:矩阵分解:奇异值分解(SVD分解)
前言 矩阵分解(Matrix Decomposition)是将一个矩阵分解成多个矩阵的乘积的过程,这种分解方法在计算、机器学习和线性代数中有广泛应用。不同的分解方式可以简化计算、揭示矩阵的内在结构或提高算法的效率。 奇异值分解 奇异值分解…...

接口测试用例设计的关键步骤与技巧解析!
简介 接口测试在需求分析完成之后,即可设计对应的接口测试用例,然后根据用例进行接口测试。接口测试用例的设计也需要用到黑盒测试用例设计方法,和测试流程与理论章节的功能测试用例设计的方法类似,设计过程中还需要增加与接口特…...

CSS画icon图标系列(一)
目录 前言: 一、向右箭头 1.原理: 2.代码实现 3.结果展示: 二、钟表 1.原理: 2.代码展示: 3.最终效果: 三、小手机 1.原理: 2.代码展示: 3.最后效果: 四、结…...

【数据结构-合法括号字符串】【华为笔试题】力扣1190. 反转每对括号间的子串
给出一个字符串 s(仅含有小写英文字母和括号)。 请你按照从括号内到外的顺序,逐层反转每对匹配括号中的字符串,并返回最终的结果。 注意,您的结果中 不应 包含任何括号。 示例 1: 输入:s “…...

qt QFileInfo详解
1、概述 QFileInfo是Qt框架中用于获取文件信息的工具类。它提供了与操作系统无关的文件属性,如文件的名称、位置(路径)、访问权限、类型(是否为目录或符号链接)等。此外,QFileInfo还可以获取文件的大小、创…...

金华迪加 现场大屏互动系统 mobile.do.php 任意文件上传漏洞复现
0x01 产品简介 金华迪加现场大屏互动系统是一种集成了先进技术和创意设计的互动展示解决方案,旨在通过大屏幕和多种交互方式,为观众提供沉浸式的互动体验。该系统广泛应用于各类活动、展览、会议等场合,能够显著提升现场氛围和参与者的体验感。 0x02 漏洞概述 金华迪加 现…...

探寻5G工业网关市场,5G工业网关品牌解析
随着5G技术的浪潮席卷全球,工业领域正经历着一场前所未有的变革。5G工业网关,作为连接工业设备与云端的桥梁,以其高速、低延迟的数据传输能力和强大的边缘计算能力,成为推动工业数字化转型的关键力量。那么,在众多5G工…...

RK3568开发板静态IP地址配置
1. 连接SSH MYD-LR3568 开发板设置了静态 eth0:1 192.168.0.10 和 eth1:1 192.168.1.10,在没有串口时调试开发板,可以用工具 SSH 登陆到开发板。 首先需要用一根网线直连电脑和开发板,或者通过路由器连接到开发板,将电脑 IP 手动设…...

element-plus table tableRowClassName 无效
官网上给的是 .el-table .warning-row {--el-table-tr-bg-color: var(--el-color-warning-light-9); } .el-table .success-row {--el-table-tr-bg-color: var(--el-color-success-light-9); } 但是 如果 加上了 scoped 这样样式是无效的 在 vue3 中用样式穿透 即可生…...

商务英语学习柯桥学外语到泓畅-老外说“go easy on me”是什么意思?
在口语中“go easy on sb ”这个短语是很常见的 01 go easy on me 怎么理解? 在口语中,“go easy on me”是一个非常常见的表达,通常表示请求对方在某方面对自己宽容一些,不要对自己太过苛刻或严厉。 短语(goÿ…...

【Python爬虫基础】基于 Python 的反爬虫机制详解与代码实现
基于 Python 的反爬虫机制详解与代码实现 在如今的信息时代,数据的重要性不言而喻。许多企业网站都包含着宝贵的数据,这些数据可能会被网络爬虫恶意抓取,这种行为不仅影响服务器的正常运行,还可能泄露商业机密。为了应对这种情况,网站开发人员需要了解并应用有效的反爬虫…...

HTB:PermX[WriteUP]
目录 连接至HTB服务器并启动靶机 1.How many TCP ports are listening on PermX? 使用nmap对靶机TCP端口进行开放扫描 2.What is the default domain name used by the web server on the box? 使用curl访问靶机80端口 3.On what subdomain of permx.htb is there an o…...

uniapp 整合 OpenLayers - 使用modify修改要素
import { Modify } from "ol/interaction"; 修改点、线、面的位置和形状核心代码: // 修改要素核心代码modifyFeature() {this.modify new Modify({source: this.lineStringLayer.getSource(),});this.map.addInteraction(this.modify);}, 完整代码&am…...

JMeter快速造数之数据导入导出
导入数据 输入表格格式如下 创建CSV Data Set Config 在Body Data中调用 { "username": "${email}", "password": "123456", "client_id": "00bb9dbfc67439a5d42e0e19f448c7de310df4c7fcde6feb5bd95c6fac5a5afc"…...

框架学习01-Spring
一、Spring框架概述 Spring是一个开源的轻量级Java开发框架,它的主要目的是为了简化企业级应用程序的开发。它提供了一系列的功能,包括控制反转(IOC)、注入(DI)、面向切面编程(AOP)…...

Java | Leetcode Java题解之第539题最小时间差
题目: 题解: class Solution {public int findMinDifference(List<String> timePoints) {int n timePoints.size();if (n > 1440) {return 0;}Collections.sort(timePoints);int ans Integer.MAX_VALUE;int t0Minutes getMinutes(timePoint…...

126页PPT麦肯锡战略实施与成本优化:质效提升与精益采购实践
麦肯锡企业PMO的各个阶段是一个结构化和系统化的过程,旨在确保项目的高效执行和成功交付。以下是麦肯锡企业PMO各个阶段的详细描述: 一、项目启动与规划阶段 此阶段的主要目标是明确项目目标、业务需求,以及制定项目章程和项目管理计划。 …...
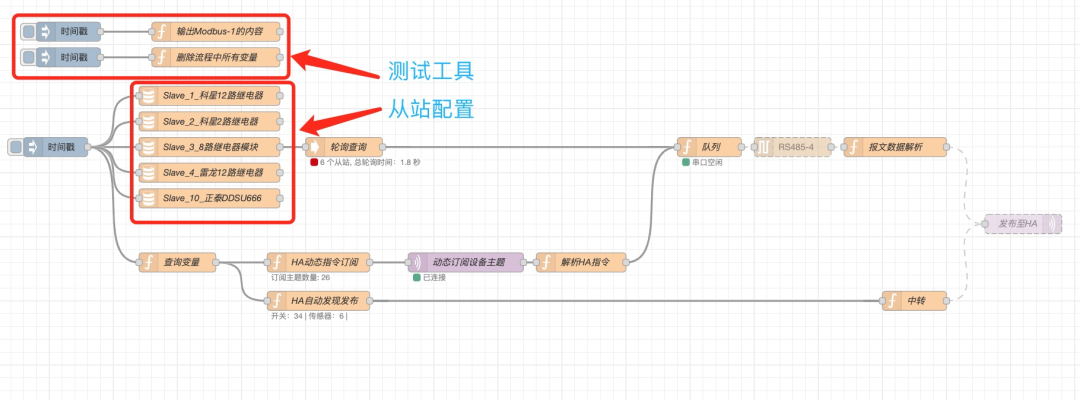
Modbus解析流程全面升级:体验全新核心与终极优化!
01 前言 本文章原文发表于我的微信公众号,请大家关注阅读,涉及的源代码等都在公众号,请搜索公众号: 智能家居NodeRed和HomeAssistant 即可关注。 02 全面改进的解析流程 前面发布过的Modbus解析流程在经过多个设备测试后发现存…...

【MWorks】Ubuntu 系统搭建
升级 Ubuntu系统 sudo apt-get update sudo apt-get upgrade安装流程 sudo chmod x 路径/文件.run安装 sudo 路径/文件.run安装过程中两个选项都填 y 打开安装对应的文件夹 运行 syslab.sh 文件,运行结束后,就可以在左上角开始搜索到syslab了。...

安装Element-Plus与v-model在vue3组件中的使用
安装Element-Plus 1.安装Element-Plus # 选择一个你喜欢的包管理器# NPM npm install element-plus --save# Yarn yarn add element-plus# pnpm pnpm install element-plus 2.main.ts中导入 import { createApp } from vue import { createPinia } from piniaimport App fr…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...
