当前位置： 首页 > news >正文

2024第三次随堂测验参考答案

news 2026/2/9 20:08:16

7-1 求一组数组中的平均数

输入10个整数，输出这10个整数的的平均数，要求输出的平均数保留2位小数

输入样例：

1 2 3 4 5 6 7 8 9 10

输出样例：

5.50

参考答案：

#include <stdio.h>
int main(){int sum = 0;for (int i = 1; i <= 10; i++) {int num;scanf("%d", &num);sum += num;}double ans = sum/10.0;printf("%.2f",ans);return 0;
}

7-2 翻转数组

输入一组数（少于50个元素），要求对该数组元素进行倒序输出。

输入格式:

第一行输入一个数n表示数组中元素个数，然后一行输入n个整数，数与数间用空格隔开。

输出格式:

将该组数倒序输出，数与数间用一个空格隔开，第一个数前无空格，最后一个数后无空格。

输入样例:

12
36 74 20 96 21 48 99 68 84 81 34 53

输出样例:

53 34 81 84 68 99 48 21 96 20 74 36

参考答案：

#include <stdio.h>
int main(){int n;scanf("%d", &n);int num[60];for (int i = 0; i < n; i++) {scanf("%d", &num[i]);}for (int i = n-1; i >= 0; i--) {if (i != n-1) printf(" ");printf("%d", num[i]);}return 0;
}

7-3 求数组中偶数之和

从键盘输入n个整数存入一维数组中，计算数组元素中所有偶数之和并输出。

输入格式:

第一行，输入整数个数n；
第二行，n 个整数，数据之间用空格隔开。

输出格式:

输出和，最后换行。

输入样例:

8
10 19 18 16 17 15 14 13

输出样例:

58

参考答案：

#include <stdio.h>
int main(){int n;scanf("%d", &n);int sum = 0;for (int i = 0; i < n; i ++) {int num;scanf("%d", &num);if (num%2 == 0) sum += num;}printf("%d", sum);return 0;
}

7-4 计算天数

本题要求编写程序计算某年某月某日是该年中的第几天。

输入格式:

输入在一行中按照格式“yyyy/mm/dd”（即“年/月/日”）给出日期。注意：闰年的判别条件是该年年份能被4整除但不能被100整除、或者能被400整除。闰年的2月有29天。

输出格式:

在一行输出日期是该年中的第几天。

输入样例1:

2009/03/02

输出样例1:

61

输入样例2:

2000/03/02

输出样例2:

62

参考答案：

#include<stdio.h>
int common_year[] = {0,31,28,31,30,31,30,31,31,30,31,30,31};
int leap_year[] = {0,31,29,31,30,31,30,31,31,30,31,30,31};
int main(){int year,month,day;scanf("%d/%d/%d",&year,&month,&day);int ans = 0;if (year%400 == 0 || (year%4 == 0 && year%100 != 0)) {for (int i = 0; i < month; i++) {ans += leap_year[i];}ans += day;}else {for (int i = 0; i < month; i++) {ans += common_year[i];}ans += day;}printf("%d",ans);return 0;
}

7-5 输出该月天数

从键盘输入一个年份year和月份month，输出该月有多少天(考虑闰年)。
提示：如果年份能被400整除，则它是闰年；如果能被4整除，而不能被100整除，则也是闰年，否则不是闰年。

输入格式:

输入任意符合范围（1月~12月）的月份和（1900年~9999年）年份，且两个值之间空格分隔。

输入样例:

2000 2

输出样例:

year = 2000 month = 2 days=29

输入样例:

2014 8

输出样例:

year = 2014 month = 8 days=31

参考答案：

#include<stdio.h>
int common_year[] = {0,31,28,31,30,31,30,31,31,30,31,30,31};
int leap_year[] = {0,31,29,31,30,31,30,31,31,30,31,30,31};
int main(){int year, month;scanf("%d %d", &year, &month);if ((year%400 == 0) || (year%4 == 0 && year%100 != 0)) {printf("year = %d month = %d days=%d", year, month, leap_year[month]);    }else {printf("year = %d month = %d days=%d", year, month, common_year[month]);    }return 0;
}

7-6 春夏秋冬

气象意义上，通常以阳历3～5月为春季(spring)，6～8月为夏季(summer)，9～11月为秋季(autumn)，12月～来年2月为冬季(winter)。请根据输入公历的年份以及月份，输出对应的季节。

输入格式:

输入的数据格式是固定的YYYYMM的形式，即：年份占4个数位，月份占2个数位，且没有不合理的输入，如2017!@#$%13^&*之类的形式。

输出格式:

输出月份对应的季节（用英文单词表示，全部用小写字母）。

输入样例1:

201901

输出样例1:

winter

输入样例2:

201807

输出样例2:

summer

参考答案：

#include<stdio.h>
int main(){int num;scanf("%d", &num);int month = num%100;if (month >= 3 && month <= 5) printf("spring");if (month >= 6 && month <= 8) printf("summer");if (month >= 9 && month <= 11) printf("autumn");if ((month >= 1 && month <= 2) || month == 12) printf("winter");return 0;
}

7-7 求N分之一序列前N项和

本题要求编写程序，计算序列 1 + 1/2 + 1/3 + ... 的前N项之和。

输入格式:

输入在一行中给出一个正整数N。

输出格式:

在一行中按照“sum = S”的格式输出部分和的值S，精确到小数点后6位。题目保证计算结果不超过双精度范围。

输入样例:

6

输出样例:

sum = 2.450000

参考答案：

#include<stdio.h>
int main(){int n;scanf("%d", &n);double sum = 0;for (int i = 1; i <= n; i ++) {sum += 1.0/i;}printf("sum = %.6f", sum);return 0;
}

7-8 求简单交错序列前N项和

本题要求编写程序,计算序列 1 - 1/4 + 1/7 - 1/10 + ... 的前N项之和。

输入格式:

输入在一行中给出一个正整数N。

输出格式:

在一行中按照“sum = S”的格式输出部分和的值S，精确到小数点后三位。题目保证计算结果不超过双精度范围。

输入样例:

10

输出样例:

sum = 0.819

参考答案：

#include<stdio.h>
int main(){int n;scanf("%d", &n);int flag = 1;double ans = 0;for (int i = 1; i <= n; i++) {ans += flag*1.0/(3*i-2);flag = -flag;}printf("sum = %.3f", ans);return 0;
}

7-9 求交错序列前N项和

本题要求编写程序，计算交错序列 1-2/3+3/5-4/7+5/9-6/11+... 的前N项之和。

输入格式:

输入在一行中给出一个正整数N。

输出格式:

在一行中输出部分和的值，结果保留三位小数。

输入样例:

5

输出样例:

0.917

参考答案：

#include<stdio.h>
int main(){int n;scanf("%d", &n);int flag = 1;double ans = 0;for (int i = 1; i <= n; i++) {ans += flag*1.0*i/(2*i-1);flag = -flag;}printf("%.3f", ans);return 0;
}

7-10 求阶乘序列前N项和

本题要求编写程序，计算序列 1!+2!+3!+⋯ 的前N项之和。

输入格式:

输入在一行中给出一个不超过12的正整数N。

输出格式:

在一行中输出整数结果。

输入样例:

5

输出样例:

153

参考答案：

#include<stdio.h>int factorial(int x) {int y = 1;for (int i = 1; i <= x; i++) {y *= i;}return y;
}int main(){int n;scanf("%d", &n);int ans = 0;for (int i = 1; i <= n; i++) {ans += factorial(i);}printf("%d", ans);return 0;
}

7-11 求分数序列前N项和

本题要求编写程序，计算序列 2/1+3/2+5/3+8/5+... 的前N项之和。注意该序列从第2项起，每一项的分子是前一项分子与分母的和，分母是前一项的分子。

输入格式:

输入在一行中给出一个正整数N。

输出格式:

在一行中输出部分和的值，精确到小数点后两位。题目保证计算结果不超过双精度范围。

输入样例:

20

输出样例:

32.66

参考答案：

#include<stdio.h>
int main(){int n;scanf("%d", &n);double ans = 0;double fenzi = 2;double fenmu = 1;for (int i = 1; i <= n; i++) {ans += fenzi/fenmu;double new_fenzi = fenzi + fenmu;double new_fenmu = fenzi;fenzi = new_fenzi;fenmu = new_fenmu;}printf("%.2f", ans);return 0;
}

7-12 素数对猜想

让我们定义dn​为：dn​=pn+1​−pn​，其中pi​是第i个素数。显然有d1​=1，且对于n>1有dn​是偶数。“素数对猜想”认为“存在无穷多对相邻且差为2的素数”。

现给定任意正整数N(<105)，请计算不超过N的满足猜想的素数对的个数。

输入格式:

输入在一行给出正整数N。

输出格式:

在一行中输出不超过N的满足猜想的素数对的个数。

输入样例:

20

输出样例:

4

参考答案：

#include<stdio.h>
#include <stdbool.h>
bool isPrime(int x) {bool flag = true;if (x == 1) flag = false;if (x == 2) flag = true;if (x > 2) {for (int i = 2; i <= sqrt(x); i++) {if (x%i == 0) {flag = false;break;}}}return flag;
}int main(){int n;scanf("%d",&n);int prime[9999];int index = 0;int ans = 0;for (int i = 1; i <= n; i++) {if (isPrime(i) == true) {prime[index] = i;index++;}}for (int i = 1; i < index; i++) {if (prime[i] - prime[i-1] == 2) {ans++;}}printf("%d",ans);
}

7-13 求n以内最大的k个素数以及它们的和

本题要求计算并输出不超过n的最大的k个素数以及它们的和。

输入格式:

输入在一行中给出n(10≤n≤10000)和k(1≤k≤10)的值。

输出格式:

在一行中按下列格式输出:

素数1+素数2+…+素数k=总和值

其中素数按递减顺序输出。若n以内不够k个素数，则按实际个数输出。

输入样例1:

1000 10

输出样例1:

997+991+983+977+971+967+953+947+941+937=9664

输入样例2:

12 6

输出样例2:

11+7+5+3+2=28

参考答案：

#include<stdio.h>
int isPrime(int x) {int flag = 1;if (x == 1) flag = 0;if (x == 2) flag = 1;if (x > 2) {for (int i = 2; i <= sqrt(x); i++) {if (x%i == 0) {flag = 0;break;}}}return flag;
}
int main(){int n, k;scanf("%d %d",&n, &k);int sum = 0;int flag = 1;while(n > 0 && k > 0) {if (isPrime(n) == 1) {if (flag == 0) printf("+");printf("%d",n);sum += n;flag = 0;k--;}n--;}printf("=%d",sum);
}

7-14 哥德巴赫猜想

哥德巴赫猜想大家都很熟悉，今日常见的猜想陈述为欧拉的版本，即任一大于2的偶数都可写成两个素数之和，亦称为“强哥德巴赫猜想”或“关于偶数的哥德巴赫猜想”。由于一个偶数可能有多组不同的素数对,所以要求输出两个彼此最接近的素数。

输入格式:

输入有多行，每一行有一个偶整数n(5<n≤10000)

输出格式:

对于每个偶数,输出两个彼此最接近的素数,其和等于该偶数(较小的素数放在较大的素数前).

输入样例:

20
30
40

输出样例:

7 13
13 17
17 23

参考答案：

#include<stdio.h>
int isPrime(int x) {int flag = 1;if (x == 1) flag = 0;if (x == 2) flag = 1;if (x > 2) {for (int i = 2; i <= sqrt(x); i++) {if (x%i == 0) {flag = 0;break;}}}return flag;
}
int main(){int n, a, b;while(scanf("%d", &n) != EOF){for(int i = n/2; i >= 1; i --){a = i;b = n-i;if(isPrime(i) == 1 && isPrime(n-i) == 1){break;}}printf("%d %d\n", a, b);}return 0;
}

7-15 数组元素循环右移问题

一个数组A中存有N（>0）个整数，在不允许使用另外数组的前提下，将每个整数循环向右移M（≥0）个位置，即将A中的数据由（A0​A1​⋯AN−1​）变换为（AN−M​⋯AN−1​A0​A1​⋯AN−M−1​）（最后M个数循环移至最前面的M个位置）。如果需要考虑程序移动数据的次数尽量少，要如何设计移动的方法？

输入格式:

每个输入包含一个测试用例，第1行输入N（1≤N≤100）和M（≥0）；第2行输入N个整数，之间用空格分隔。

输出格式:

在一行中输出循环右移M位以后的整数序列，之间用空格分隔，序列结尾不能有多余空格。

输入样例:

6 2
1 2 3 4 5 6

输出样例:

5 6 1 2 3 4

参考答案：

#include<stdio.h>
int main(){int n, m;scanf("%d %d", &n, &m);int num[110];for (int i = 0; i < n; i++) scanf("%d", &num[i]);for (int i = 0; i < m; i++) {int temp = num[n-1];for (int j = n-1; j > 0; j--) {num[j] = num[j-1];}num[0] = temp;}for (int i = 0; i < n; i++) {if (i != 0) printf(" ");printf("%d", num[i]);}return 0;
}

7-16 猴子选大王

一群猴子要选新猴王。新猴王的选择方法是：让N只候选猴子围成一圈，从某位置起顺序编号为1~N号。从第1号开始报数，每轮从1报到3，凡报到3的猴子即退出圈子，接着又从紧邻的下一只猴子开始同样的报数。如此不断循环，最后剩下的一只猴子就选为猴王。请问是原来第几号猴子当选猴王？

输入格式：

输入在一行中给一个正整数N（≤1000）。

输出格式：

在一行中输出当选猴王的编号。

输入样例：

11

输出样例：

7

参考答案：

#include<stdio.h>
int flag[1010] = {0};
int main(){int n;scanf("%d", &n);int cnt = 0;int total = n;while(total > 1) {for (int i = 1; i <= n; i++) {if (flag[i] == 1) continue;if (flag[i] == 0) cnt++;if (cnt == 3) {flag[i] = 1;cnt = 0;total--;}}}for (int i = 1; i <= n; i++) {if (flag[i] == 0) {printf("%d", i);break;}}return 0;
}

7-17 数组循环左移

本题要求实现一个对数组进行循环左移的简单函数：一个数组a中存有n（>0）个整数，在不允许使用另外数组的前提下，将每个整数循环向左移m（≥0）个位置，即将a中的数据由（a0​a1​⋯an−1​）变换为（am​⋯an−1​a0​a1​⋯am−1​）（最前面的m个数循环移至最后面的m个位置）。如果还需要考虑程序移动数据的次数尽量少，要如何设计移动的方法？

输入格式:

输入第1行给出正整数n（≤100）和整数m（≥0）；第2行给出n个整数，其间以空格分隔。

输出格式:

在一行中输出循环左移m位以后的整数序列，之间用空格分隔，序列结尾不能有多余空格。

输入样例：

8 3
1 2 3 4 5 6 7 8

输出样例：

4 5 6 7 8 1 2 3

参考答案：

#include<stdio.h>
int main(){int n, m;scanf("%d %d", &n, &m);int num[1010];for (int i = 0; i < n; i++) scanf("%d", &num[i]);for (int i = 0; i < m; i++) {int temp = num[0];for (int j = 0; j < n-1; j++) {num[j] = num[j+1];}num[n-1] = temp;}for (int i = 0; i < n; i++) {if (i != 0) printf(" ");printf("%d", num[i]);}return 0;
}

7-18 利用数组计算斐波那契数列

本题要求编写程序，利用数组计算菲波那契（Fibonacci）数列的前N项，每行输出5个，题目保证计算结果在长整型范围内。Fibonacci数列就是满足任一项数字是前两项的和（最开始两项均定义为1）的数列，例如：：1，1，2，3，5，8，13，...。

输入格式:

输入在一行中给出一个整数N（1≤N≤46）。

输出格式:

输出前N个Fibonacci数，每个数占11位，每行输出5个。如果最后一行输出的个数不到5个，也需要换行。

如果输入的N不在有效范围内，则输出"Invalid."。

输入样例1:

7

输出样例1:

          1          1          2          3          58         13

输入样例2:

0

输出样例2:

Invalid.

参考答案：

#include<stdio.h>
int main(){int n;scanf("%d", &n);int num[50];num[1] = 1;num[2] = 1;if (n < 1 || n > 46) {printf("Invalid.");return 0;}if (n >= 3) {for (int i = 3; i <= n; i++) {num[i] = num[i-1] + num[i-2];}}for (int i = 1; i <= n; i++) {printf("%11d", num[i]);if (i%5 == 0 || i == n) printf("\n");}return 0;
}

相关文章：

2024第三次随堂测验参考答案

7-1 求一组数组中的平均数 输入10个整数&#xff0c;输出这10个整数的的平均数&#xff0c;要求输出的平均数保留2位小数 输入样例&#xff1a; 1 2 3 4 5 6 7 8 9 10 输出样例&#xff1a; 5.50 参考答案&#xff1a; #include <stdio.h> int main(){int sum 0;…...

编程日记 2024/11/6 16:07:27

期权交易策略 v0.1

一.概述 1.参考 <期权波动率与定价> 2.期权价格 标的现价100元,到期日价格可能情况如下。 价格 80 90 100 110 120 概率 20% 20% 20% 20% 20% 持有标的时,期望收益为0.如果持有100的看涨期权&#xff0c;忽略期权费&#xff0c;期望收益为(100-100)*0.2…...

编程日记 2024/11/6 16:06:26

pytorch学习：矩阵分解：奇异值分解（SVD分解）

前言 矩阵分解&#xff08;Matrix Decomposition&#xff09;是将一个矩阵分解成多个矩阵的乘积的过程&#xff0c;这种分解方法在计算、机器学习和线性代数中有广泛应用。不同的分解方式可以简化计算、揭示矩阵的内在结构或提高算法的效率。 奇异值分解 奇异值分解&#xf…...

编程日记 2024/11/6 16:02:21

接口测试用例设计的关键步骤与技巧解析！

简介 接口测试在需求分析完成之后&#xff0c;即可设计对应的接口测试用例&#xff0c;然后根据用例进行接口测试。接口测试用例的设计也需要用到黑盒测试用例设计方法&#xff0c;和测试流程与理论章节的功能测试用例设计的方法类似&#xff0c;设计过程中还需要增加与接口特…...

编程日记 2024/11/6 16:01:20

CSS画icon图标系列（一）

目录 前言&#xff1a; 一、向右箭头 1.原理&#xff1a; 2.代码实现 3.结果展示&#xff1a; 二、钟表 1.原理&#xff1a; 2.代码展示&#xff1a; 3.最终效果&#xff1a; 三、小手机 1.原理&#xff1a; 2.代码展示&#xff1a; 3.最后效果&#xff1a; 四、结…...

编程日记 2024/11/6 15:57:14

【数据结构-合法括号字符串】【华为笔试题】力扣1190. 反转每对括号间的子串

给出一个字符串 s&#xff08;仅含有小写英文字母和括号&#xff09;。 请你按照从括号内到外的顺序&#xff0c;逐层反转每对匹配括号中的字符串&#xff0c;并返回最终的结果。 注意&#xff0c;您的结果中 不应 包含任何括号。 示例 1&#xff1a; 输入&#xff1a;s “…...

编程日记 2024/11/6 15:55:12

qt QFileInfo详解

1、概述 QFileInfo是Qt框架中用于获取文件信息的工具类。它提供了与操作系统无关的文件属性&#xff0c;如文件的名称、位置&#xff08;路径&#xff09;、访问权限、类型&#xff08;是否为目录或符号链接&#xff09;等。此外&#xff0c;QFileInfo还可以获取文件的大小、创…...

编程日记 2024/11/6 15:53:09

金华迪加 现场大屏互动系统 mobile.do.php 任意文件上传漏洞复现

0x01 产品简介 金华迪加现场大屏互动系统是一种集成了先进技术和创意设计的互动展示解决方案，旨在通过大屏幕和多种交互方式，为观众提供沉浸式的互动体验。该系统广泛应用于各类活动、展览、会议等场合，能够显著提升现场氛围和参与者的体验感。 0x02 漏洞概述 金华迪加 现…...

编程日记 2024/11/6 15:51:07

探寻5G工业网关市场，5G工业网关品牌解析

随着5G技术的浪潮席卷全球&#xff0c;工业领域正经历着一场前所未有的变革。5G工业网关&#xff0c;作为连接工业设备与云端的桥梁&#xff0c;以其高速、低延迟的数据传输能力和强大的边缘计算能力&#xff0c;成为推动工业数字化转型的关键力量。那么&#xff0c;在众多5G工…...

编程日记 2024/11/6 15:50:06

RK3568开发板静态IP地址配置

1. 连接SSH MYD-LR3568 开发板设置了静态 eth0:1 192.168.0.10 和 eth1:1 192.168.1.10&#xff0c;在没有串口时调试开发板&#xff0c;可以用工具 SSH 登陆到开发板。 首先需要用一根网线直连电脑和开发板&#xff0c;或者通过路由器连接到开发板&#xff0c;将电脑 IP 手动设…...

编程日记 2024/11/6 15:49:05

element-plus table tableRowClassName 无效

官网上给的是 .el-table .warning-row {--el-table-tr-bg-color: var(--el-color-warning-light-9); } .el-table .success-row {--el-table-tr-bg-color: var(--el-color-success-light-9); } 但是 如果 加上了 scoped 这样样式是无效的 在 vue3 中用样式穿透 即可生…...

编程日记 2024/11/6 15:48:03

商务英语学习柯桥学外语到泓畅-老外说“go easy on me”是什么意思？

在口语中“go easy on sb ”这个短语是很常见的 01 go easy on me 怎么理解&#xff1f; 在口语中&#xff0c;“go easy on me”是一个非常常见的表达&#xff0c;通常表示请求对方在某方面对自己宽容一些&#xff0c;不要对自己太过苛刻或严厉。 短语&#xff08;go&#xff…...

编程日记 2024/11/6 15:47:01

【Python爬虫基础】基于 Python 的反爬虫机制详解与代码实现

基于 Python 的反爬虫机制详解与代码实现 在如今的信息时代，数据的重要性不言而喻。许多企业网站都包含着宝贵的数据，这些数据可能会被网络爬虫恶意抓取，这种行为不仅影响服务器的正常运行，还可能泄露商业机密。为了应对这种情况，网站开发人员需要了解并应用有效的反爬虫…...

编程日记 2024/11/6 15:45:59

HTB：PermX[WriteUP]

目录 连接至HTB服务器并启动靶机 1.How many TCP ports are listening on PermX? 使用nmap对靶机TCP端口进行开放扫描 2.What is the default domain name used by the web server on the box? 使用curl访问靶机80端口 3.On what subdomain of permx.htb is there an o…...

编程日记 2024/11/6 15:43:57

uniapp 整合 OpenLayers - 使用modify修改要素

import { Modify } from "ol/interaction"; 修改点、线、面的位置和形状核心代码&#xff1a; // 修改要素核心代码modifyFeature() {this.modify new Modify({source: this.lineStringLayer.getSource(),});this.map.addInteraction(this.modify);}, 完整代码&am…...

编程日记 2024/11/6 15:41:55

JMeter快速造数之数据导入导出

导入数据 输入表格格式如下 创建CSV Data Set Config 在Body Data中调用 { "username": "${email}", "password": "123456", "client_id": "00bb9dbfc67439a5d42e0e19f448c7de310df4c7fcde6feb5bd95c6fac5a5afc"…...

编程日记 2024/11/6 15:38:51

框架学习01-Spring

一、Spring框架概述 Spring是一个开源的轻量级Java开发框架&#xff0c;它的主要目的是为了简化企业级应用程序的开发。它提供了一系列的功能&#xff0c;包括控制反转&#xff08;IOC&#xff09;、注入&#xff08;DI&#xff09;、面向切面编程&#xff08;AOP&#xff09;…...

编程日记 2024/11/6 15:37:50

Java | Leetcode Java题解之第539题最小时间差

题目&#xff1a; 题解&#xff1a; class Solution {public int findMinDifference(List<String> timePoints) {int n timePoints.size();if (n > 1440) {return 0;}Collections.sort(timePoints);int ans Integer.MAX_VALUE;int t0Minutes getMinutes(timePoint…...

编程日记 2024/11/6 15:34:44

126页PPT麦肯锡战略实施与成本优化：质效提升与精益采购实践

麦肯锡企业PMO的各个阶段是一个结构化和系统化的过程&#xff0c;旨在确保项目的高效执行和成功交付。以下是麦肯锡企业PMO各个阶段的详细描述&#xff1a; 一、项目启动与规划阶段 此阶段的主要目标是明确项目目标、业务需求&#xff0c;以及制定项目章程和项目管理计划。 …...

编程日记 2024/11/6 15:33:43

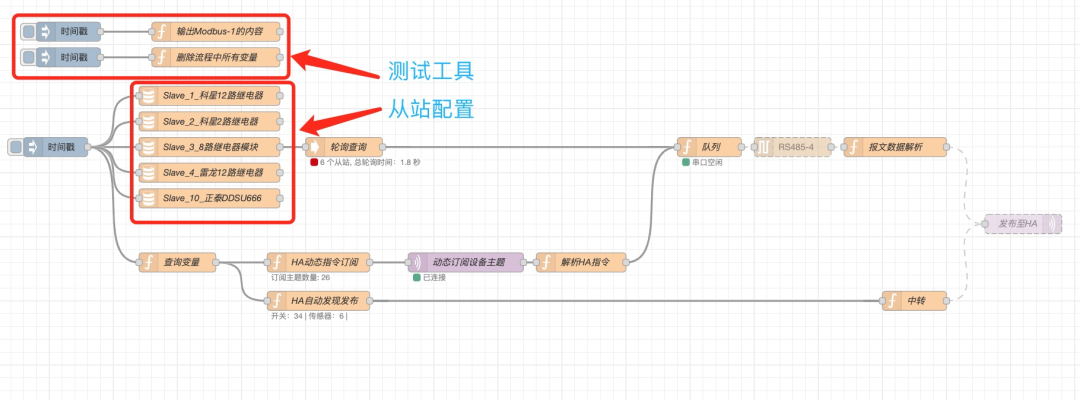
Modbus解析流程全面升级：体验全新核心与终极优化！

01 前言 本文章原文发表于我的微信公众号&#xff0c;请大家关注阅读&#xff0c;涉及的源代码等都在公众号&#xff0c;请搜索公众号&#xff1a; 智能家居NodeRed和HomeAssistant 即可关注。 02 全面改进的解析流程 前面发布过的Modbus解析流程在经过多个设备测试后发现存…...

编程日记 2024/11/6 15:31:41

脑机新手指南（八）：OpenBCI_GUI：从环境搭建到数据可视化（下）

一、数据处理与分析实战 &#xff08;一&#xff09;实时滤波与参数调整 基础滤波操作 60Hz 工频滤波&#xff1a;勾选界面右侧 “60Hz” 复选框&#xff0c;可有效抑制电网干扰&#xff08;适用于北美地区&#xff0c;欧洲用户可调整为 50Hz&#xff09;。 平滑处理&…...

编程新知 2025/11/19 22:56:53

【Oracle APEX开发小技巧12】

有如下需求&#xff1a; 有一个问题反馈页面&#xff0c;要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据&#xff0c;方便管理员及时处理反馈。 我的方法&#xff1a;直接将逻辑写在SQL中&#xff0c;这样可以直接在页面展示 完整代码&#xff1a; SELECTSF.FE…...

编程新知 2026/2/7 17:35:15

三维GIS开发cesium智慧地铁教程（5）Cesium相机控制

一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点&#xff1a; 路径验证&#xff1a;确保相对路径.…...

编程新知 2025/12/1 19:23:04

如何在看板中体现优先级变化

在看板中有效体现优先级变化的关键措施包括&#xff1a;采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中&#xff0c;设置任务排序规则尤其重要&#xff0c;因为它让看板视觉上直观地体…...

编程新知 2026/1/23 12:42:28

五年级数学知识边界总结思考-下册

目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解&#xff1a;由来、作用与意义**一、知识点核心内容****二、知识点的由来&#xff1a;从生活实践到数学抽象****三、知识的作用&#xff1a;解决实际问题的工具****四、学习的意义&#xff1a;培养核心素养…...

编程新知 2025/10/7 4:57:55

Python爬虫（一）：爬虫伪装

一、网站防爬机制概述 在当今互联网环境中&#xff0c;具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类&#xff1a; 身份验证机制&#xff1a;直接将未经授权的爬虫阻挡在外反爬技术体系&#xff1a;通过各种技术手段增加爬虫获取数据的难度…...

编程新知 2026/1/30 20:42:46

鱼香ros docker配置镜像报错：https://registry-1.docker.io/v2/

使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题&#xff1a;docker pull 失败 网络不同&#xff0c;需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

编程新知 2025/12/31 6:28:08

大数据学习（132）-HIve数据分析

​​​​&#x1f34b;&#x1f34b;大数据学习&#x1f34b;&#x1f34b; &#x1f525;系列专栏&#xff1a; &#x1f451;哲学语录: 用力所能及&#xff0c;改变世界。 &#x1f496;如果觉得博主的文章还不错的话&#xff0c;请点赞&#x1f44d;收藏⭐️留言&#x1f4…...

编程新知 2025/10/7 8:52:21

智能分布式爬虫的数据处理流水线优化：基于深度强化学习的数据质量控制

在数字化浪潮席卷全球的今天&#xff0c;数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具&#xff0c;在大规模数据获取中发挥着关键作用。然而&#xff0c;传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时&#xff0c;常出现数据质…...

编程新知 2026/2/6 1:04:23

均衡后的SNRSINR

本文主要摘自参考文献中的前两篇&#xff0c;相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程&#xff0c;其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt​ 根发送天线&#xff0c; n r n_r nr​ 根接收天线的 MIMO 系…...

编程新知 2026/1/30 4:47:24