代码随想录算法训练营第三十八天|Day38 动态规划
322. 零钱兑换
视频讲解:https://www.bilibili.com/video/BV14K411R7yv
https://programmercarl.com/0322.%E9%9B%B6%E9%92%B1%E5%85%91%E6%8D%A2.html
思路
#define min(a, b) ((a) > (b) ? (b) : (a))
int coinChange(int* coins, int coinsSize, int amount) {int* dp = (int*)malloc(sizeof(int) * (amount + 1));for (int j = 0; j < amount + 1; j++) {dp[j] = INT_MAX;}dp[0] = 0;for(int i = 0; i <= amount; i++){for(int j = 0; j < coinsSize; j++){if(i - coins[j] >= 0 && dp[i - coins[j]] != INT_MAX){dp[i] = min(dp[i], dp[i - coins[j]] + 1);}}}if(dp[amount] == INT_MAX){return -1;}return dp[amount];
}学习反思
动态规划解决硬币找零问题的实现。函数coinChange接受三个参数:coins表示可用的硬币面额,coinsSize表示硬币种类数量,amount表示要找零的金额。首先,代码定义了一个大小为(amount + 1)的数组dp,用来保存每个金额所需的最少硬币数。然后将dp数组的所有元素初始化为INT_MAX,表示暂时无法找零。接下来,将dp[0]初始化为0,表示找零金额为0时不需要任何硬币。然后,通过两层嵌套循环遍历所有金额,以及所有硬币面额,计算每个金额所需的最少硬币数。如果当前金额减去某个硬币面额大于等于0,并且之前的金额所需的最少硬币数不等于INT_MAX(表示该金额无法找零),则更新当前金额所需的最少硬币数。这个更新的过程通过min宏来实现,它选择较小的值作为新的最少硬币数。最后,判断最后一个金额所需的最少硬币数是否等于INT_MAX,如果是,则表示无法找零,返回-1;否则,返回最后一个金额所需的最少硬币数。
279.完全平方数
视频讲解:https://www.bilibili.com/video/BV12P411T7Br
https://programmercarl.com/0279.%E5%AE%8C%E5%85%A8%E5%B9%B3%E6%96%B9%E6%95%B0.html
思路
#define min(a, b) ((a) > (b) ? (b) : (a))
int numSquares(int n) {int* dp = (int*)malloc(sizeof(int) * (n + 1));for (int j = 0; j < n + 1; j++) {dp[j] = INT_MAX;}dp[0] = 0;for (int i = 0; i <= n; ++i) {for (int j = 1; j * j <= i; ++j) {dp[i] = min(dp[i - j * j] + 1, dp[i]);}}return dp[n];
}学习反思
动态规划解决完全平方数问题的实现。函数numSquares接受一个参数n,表示要判断的数。首先,代码定义了一个大小为(n + 1)的数组dp,用来保存每个数最少需要的完全平方数的个数。然后将dp数组的所有元素初始化为INT_MAX,表示暂时无法求解。接下来,将dp[0]初始化为0,表示数字0不需要任何完全平方数。然后,通过两层嵌套循环遍历所有数字,以及所有完全平方数。如果一个完全平方数的平方小于等于当前数字i,则更新当前数字需要的最少完全平方数个数。更新的过程通过min宏来实现,它选择较小的值作为新的最少完全平方数个数。最后,返回数组dp的最后一个元素,它保存了n所需的最少完全平方数个数。
139.单词拆分
视频讲解:https://www.bilibili.com/video/BV1pd4y147Rh
https://programmercarl.com/0139.%E5%8D%95%E8%AF%8D%E6%8B%86%E5%88%86.html
思路
bool wordBreak(char* s, char** wordDict, int wordDictSize) {int len = strlen(s); bool dp[len + 1];memset(dp, false, sizeof (dp));dp[0] = true;for (int i = 1; i < len + 1; ++i) {for(int j = 0; j < wordDictSize; j++){int wordLen = strlen(wordDict[j]);int k = i - wordLen;if(k < 0){continue;}dp[i] = (dp[k] && !strncmp(s + k, wordDict[j], wordLen)) || dp[i];}}return dp[len];
}学习反思
动态规划解决单词拆分问题的实现。函数wordBreak接受三个参数,分别是字符串s、字符串数组wordDict和wordDict的大小wordDictSize。首先,代码定义了一个长度为len + 1的bool型数组dp,用来保存 s 的前 i 个字符能否被拆分成字典中的单词。然后将dp数组的所有元素初始化为false,表示暂时无法拆分。接下来,将dp[0]初始化为true,表示空字符串可被拆分。然后,通过两层嵌套循环遍历每个字符以及字典中的单词。对于每个字符 i,再内层循环遍历字典中的单词。如果当前字符 i 减去单词长度 wordLen 大于等于 0,并且字典中的单词与 s 中的子串相等,则更新 dp[i] 为 true。这里使用了strncmp函数来比较字符串的子串是否与字典中的单词相等。最后,返回 dp[len],它表示整个字符串 s 能否被拆分。
背包问题总结篇!
在进行背包问题的时候,我们都是按照如下五部来逐步分析,相信大家也体会到,把这五部都搞透了,算是对动规来理解深入了。
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
其实这五部里哪一步都很关键,但确定递推公式和确定遍历顺序都具有规律性和代表性,所以下面从这两点来对背包问题做一做总结。背包递推公式
问能否能装满背包(或者最多装多少):dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]); ,对应题目如下:
- 动态规划:416.分割等和子集(opens new window)
- 动态规划:1049.最后一块石头的重量 II(opens new window)
问装满背包有几种方法:dp[j] += dp[j - nums[i]] ,对应题目如下:
- 动态规划:494.目标和(opens new window)
- 动态规划:518. 零钱兑换 II(opens new window)
- 动态规划:377.组合总和Ⅳ(opens new window)
- 动态规划:70. 爬楼梯进阶版(完全背包)(opens new window)
问背包装满最大价值:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); ,对应题目如下:
- 动态规划:474.一和零(opens new window)
问装满背包所有物品的最小个数:dp[j] = min(dp[j - coins[i]] + 1, dp[j]); ,对应题目如下:
- 动态规划:322.零钱兑换(opens new window)
- 动态规划:279.完全平方数(opens new window)
遍历顺序
01背包
在动态规划:关于01背包问题,你该了解这些! (opens new window)中我们讲解二维dp数组01背包先遍历物品还是先遍历背包都是可以的,且第二层for循环是从小到大遍历。
和动态规划:关于01背包问题,你该了解这些!(滚动数组) (opens new window)中,我们讲解一维dp数组01背包只能先遍历物品再遍历背包容量,且第二层for循环是从大到小遍历。
一维dp数组的背包在遍历顺序上和二维dp数组实现的01背包其实是有很大差异的,大家需要注意!
完全背包
说完01背包,再看看完全背包。
在动态规划:关于完全背包,你该了解这些! (opens new window)中,讲解了纯完全背包的一维dp数组实现,先遍历物品还是先遍历背包都是可以的,且第二层for循环是从小到大遍历。
但是仅仅是纯完全背包的遍历顺序是这样的,题目稍有变化,两个for循环的先后顺序就不一样了。
如果求组合数就是外层for循环遍历物品,内层for遍历背包。
如果求排列数就是外层for遍历背包,内层for循环遍历物品。
相关题目如下:
- 求组合数:动态规划:518.零钱兑换II(opens new window)
- 求排列数:动态规划:377. 组合总和 Ⅳ (opens new window)、动态规划:70. 爬楼梯进阶版(完全背包)(opens new window)
如果求最小数,那么两层for循环的先后顺序就无所谓了,相关题目如下:
- 求最小数:动态规划:322. 零钱兑换 (opens new window)、动态规划:279.完全平方数(opens new window)
对于背包问题,其实递推公式算是容易的,难是难在遍历顺序上,如果把遍历顺序搞透,才算是真正理解了。
总结
这篇背包问题总结篇是对背包问题的高度概括,讲最关键的两部:递推公式和遍历顺序,结合力扣上的题目全都抽象出来了。
而且每一个点,都进行了对应的力扣题目。
加油!!!!
相关文章:

代码随想录算法训练营第三十八天|Day38 动态规划
322. 零钱兑换 视频讲解:https://www.bilibili.com/video/BV14K411R7yv https://programmercarl.com/0322.%E9%9B%B6%E9%92%B1%E5%85%91%E6%8D%A2.html 思路 #define min(a, b) ((a) > (b) ? (b) : (a)) int coinChange(int* coins, int coinsSize, int amount…...
)
使用C++和libcurl库实现HTTP请求(GET、POST、文件上传)
在现代软件开发中,与外部API服务进行通信已成为常见需求。本文将展示如何使用C和libcurl库实现基本的HTTP请求,包括GET请求、POST请求(带JSON数据)以及包含文件上传的POST请求。 准备工作 首先,需要确保已安装libcur…...

makefile例子
$指代当前目标,就是Make命令当前构建的那个目标。比如,make foo的 $ 就指代foo。 $< 指代第一个前置条件。比如,规则为 t: p1 p2,那么$< 就指代p1。 $? 指代比目标更新的所有前置条件,之间以空格分隔。比如&a…...

用环形数组实现队列(多种高级方法,由浅入深)
同普通数组实现的队列相比,普通数组的头结点和尾节点都是固定的,在进行移除的时候如果移除了一个节点,后面所有节点都需要进行移除操作,需要的时间复杂度更高 在环形数组中,确定了头尾指针的环形数组很好地解决了这一…...

springboot框架使用RabbitMQ举例代码
以前分享过一个理论有兴趣的小伙伴可以看下 https://blog.csdn.net/Drug_/article/details/138164180 不多说 还是直接上代码 第一步:引入依赖 可以不指定版本 <!-- amqp --><dependency><groupId>org.springframework.boot</groupId…...

Java实现一个延时队列
文章目录 前言正文一、基本概念1.1 延时队列的特点1.2 常见的实现方式 二、Java原生的内存型延时队列2.1 定义延时元素DelayedElement2.2 定义延时队列管理器DelayedQueueManager2.3 消费元素2.4 调试2.5 调试结果2.6 精髓之 DelayQueue.poll() 三、基于Redisson的延时队列3.1 …...

为什么说vue是双向数据流
Vue.js 被称为 双向数据绑定(two-way data binding),是因为它支持数据在 视图(View) 和 模型(Model) 之间双向流动。这意味着,当 数据变化 时,视图会自动更新;…...

创造属于你的 Claude Prompt 和个性化 SVG 卡片|对李继刚老师提示词的浅浅解析与总结
❤️ 如果你也关注大模型与 AI 的发展现状,且对大模型应用开发非常感兴趣,我会快速跟你分享最新的感兴趣的 AI 应用和热点信息,也会不定期分享自己的想法和开源实例,欢迎关注我哦! 🥦 微信公众号ÿ…...

redis与本地缓存
本地缓存是将数据存储在应用程序所在的本地内存中的缓存方式。既然,已经有了 Redis 可以实现分布式缓存了,为什么还需要本地缓存呢?接下来,我们一起来看。 为什么需要本地缓存? 尽管已经有 Redis 缓存了,但…...

git撤销commit和add
撤销commit git reset --soft HEAD^撤销add git reset .查看状态 git status...
【361】基于springboot的招生宣传管理系统
摘 要 使用旧方法对招生宣传管理系统的信息进行系统化管理已经不再让人们信赖了,把现在的网络信息技术运用在招生宣传管理系统的管理上面可以解决许多信息管理上面的难题,比如处理数据时间很长,数据存在错误不能及时纠正等问题。这次开发的招…...

【一些关于Python的信息和帮助】
Python是一种广泛使用的高级编程语言,它的设计哲学强调代码的可读性和简洁的语法(尤其是使用空格缩进划分代码块,而不是使用大括号或关键字)。Python支持多种编程范式,包括面向对象、命令式、函数式和过程式编程。 以…...

creo toolkit二次开发学习之程序集(ProAsmcomp)和装配体组件路径对象(ProAsmcomppath)
程序集ProAsmcomp可以理解为装配体组件对象。 对象ProAssembly是ProSolid的一个实例,并共享相同的声明。因此,ProAssembly对象可以作为适用于装配体的任何ProSolid和ProMdl函数的输入。特别是,因为你可以使用函数ProSolidFeatVisit()来遍历特…...

深入浅出 Spring Boot 与 Shiro:构建安全认证与权限管理框架
一、Shiro框架概念 (一)Shiro框架概念 1.概念: Shiro是apache旗下一个开源安全框架,它对软件系统中的安全认证相关功能进行了封装,实现了用户身份认证,权限授权、加密、会话管理等功能,组成一…...

外包干了三年,精神严重内耗...
前段时间我同事(做测试的一个妹子)跟我讲,感觉早上起来十分的疲惫,不想上班,问我们这是什么样的现象,其实有时候我也有这种感觉,虽然我卷,但我也是肉体凡胎啊!不是机器人…...

ruoyi-vue集成tianai-captcha验证码
后端代码 官方使用demo文档:http://doc.captcha.tianai.cloud/#%E4%BD%BF%E7%94%A8demo 我的完整代码:https://gitee.com/Min-Duck/RuoYi-Vue.git 主pom.xml 加入依赖 <!-- 滑块验证码 --><dependency><groupId>cloud.tianai.captc…...

Django安装
在终端创建django项目 1.查看自己的python版本 输入对应自己本机python的版本,列如我的是3.11.8 先再全局安装django依赖包 2.在控制窗口输入安装命令: pip3.11 install django 看到Successflully 说明我们就安装成功了 python的Scripts文件用于存…...

Ubuntu 20.04 安装 QGC v4.3 开发环境
Ubuntu 20.04 安装 QGC开发环境 1. 准备安装 Qt 5.15.2安装依赖获取源码 2. 编译参考 前言 QGC ( QGroundControl) 是一个开源地面站,基于QT开发的,有跨平台的功能。可以在Windows,Android,MacOS或Linux上运行。它可以将PX4固件加…...
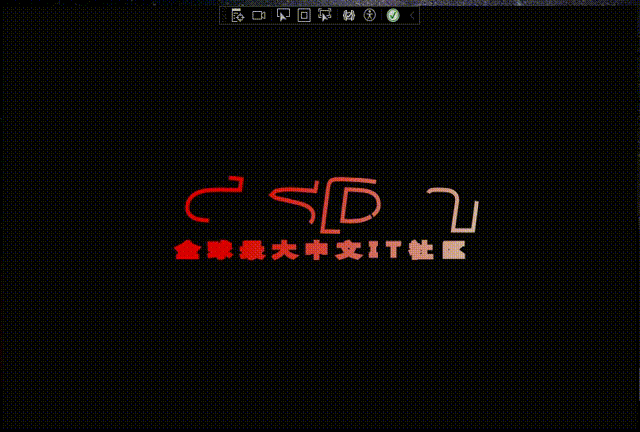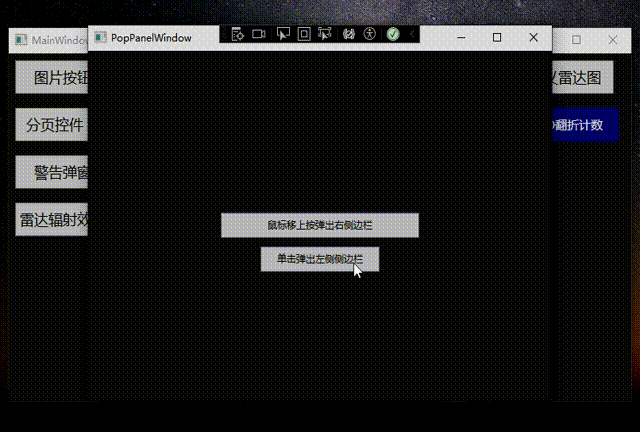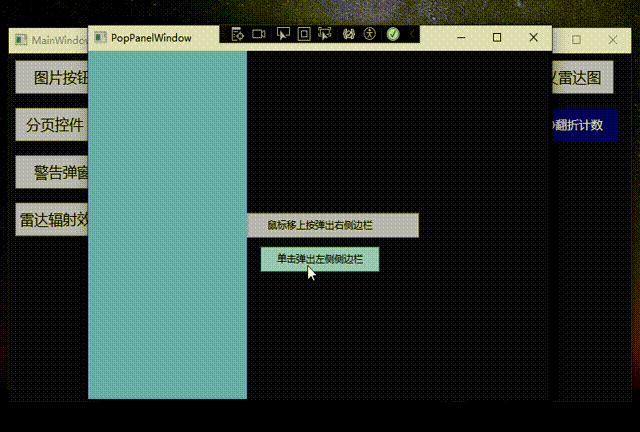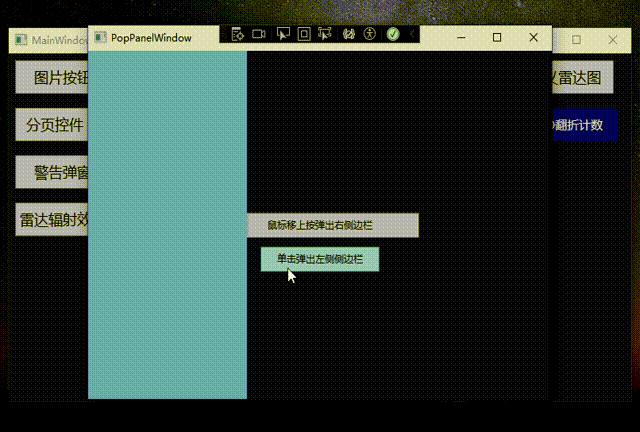
WPF+MVVM案例实战(二十一)- 制作一个侧边弹窗栏(AB类)
文章目录 1、案例效果1、侧边栏分类2、AB类侧边弹窗实现1.文件创建2、样式代码与功能代码实现3、功能代码实现 3 运行效果4、源代码获取 1、案例效果 1、侧边栏分类 A类 :左侧弹出侧边栏B类 :右侧弹出侧边栏C类 :顶部弹出侧边栏D类 …...

linux中怎样登录mysql数据库
在Linux中登录MySQL数据库,可以使用以下命令: mysql -u username -p 其中,username是你的MySQL用户名。运行该命令后,系统会提示你输入密码。 如果MySQL服务器不在本地主机或者你需要指定不同的端口,可以使用以下命…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...
