【自学笔记】神经网络(1)
文章目录
- 介绍
- 模型结构
- 层(Layer)
- 神经元
- 前向传播
- 反向传播
- Q1: 为什么要用向量
- Q2: 不用激活函数会发生什么
介绍
我们已经学习了简单的分类任务和回归任务,也认识了逻辑回归和正则化等技巧,已经可以搭建一个简单的神经网络模型了。
神经网络模仿人类神经元,进行运算、激活、传递等一系列行为,最终得到结果。这些将在之后详细讲述
模型结构
层(Layer)
一个完整的神经网络由许多层(layer)组成,除了输入层和输出层,中间的层被统称为隐藏层(Hidden Layers),具体根据功能不同有不同的名字。
神经元
一个层由许多神经元组成,一层中神经元的数量称为这一层的宽度。
比如,样本特征有“桌子的长 a a a”和“桌子的宽 b b b”,标签为"桌子的面积 s s s",则我们可以画出这样的图(举个例子):

每一个神经元要做的最基本的事情,就是获取上一个神经元的输入,经过计算,给出一个信号给下一个神经元。
前向传播
前向传播就是接收输入后,经过一系列神经元的计算,再输出的整个过程。最简单的,我们设每个神经元使用最简单的线性回归模型:
输入向量 x ( i ) x^{(i)} x(i)
f j ( i ) ( x ( i ) ) = w j ( i ) ⋅ x ( i ) + b j ( i ) f^{(i)}_{j}(x^{(i)}) = w^{(i)}_{j} \cdot x^{(i)} + b^{(i)}_{j} fj(i)(x(i))=wj(i)⋅x(i)+bj(i)
这里 w j ( i ) w^{(i)}_{j} wj(i)和 b j ( i ) b^{(i)}_{j} bj(i)都是神经元上附带的参数, i i i是层的编号, j j j是神经元的编号
通常计算出 f f f后,得到的结果会再经过一个激活函数 g g g,来实现非线性的拟合,我们以 S i g m o i d Sigmoid Sigmoid函数为例:
g ( z ) = 1 1 + e − z g(z) = \frac{1}{1+e^{-z}} g(z)=1+e−z1
回顾一下 S i g m o i d Sigmoid Sigmoid函数的性质:
g ′ ( z ) = g ( z ) ∗ [ 1 − g ( z ) ] g'(z) = g(z) * [1-g(z)] g′(z)=g(z)∗[1−g(z)]
然后这一层得到的结果作为输入进入下一层:
x ( i + 1 ) = [ g ( f 1 ( i ) ( x ( i ) ) ) g ( f 2 ( i ) ( x ( i ) ) ) . . . g ( f k i ( i ) ( x ( i ) ) ) ] x^{(i+1)}=\begin{bmatrix}g(f^{(i)}_{1}(x^{(i)}))\\g(f^{(i)}_{2}(x^{(i)}))\\...\\g(f^{(i)}_{k_{i}}(x^{(i)}))\end{bmatrix} x(i+1)= g(f1(i)(x(i)))g(f2(i)(x(i)))...g(fki(i)(x(i)))
除了Sigmoid函数,Relu函数也经常被使用:
g ( z ) = { z i f z ≥ 0 , 0 i f z < 0 = m a x ( 0 , z ) g(z)=\begin{cases}z \ \ if \ z \ge 0, \\0 \ \ if \ z < 0 \end{cases} = max(0, z) g(z)={z if z≥0,0 if z<0=max(0,z)

由于它的导数非常简单,可以加速收敛;更重要的是它可以避免梯度消失问题,这个之后再讲。
在最后的输出层时,我们通常使用另一个激活函数 S o f t m a x Softmax Softmax
S o f t m a x : x = [ x 1 , x 2 , . . . , x k ] → y = [ y 1 , y 2 , . . . , y k ] Softmax: x = [x_{1}, x_{2}, ..., x_{k}] \to y = [y_{1}, y_{2}, ..., y_{k}] Softmax:x=[x1,x2,...,xk]→y=[y1,y2,...,yk]
s u c h t h a t y i = x i ∑ j = 1 k x j such \ that \ y_{i}=\frac{x_{i}}{\sum_{j=1}^{k}x_{j}} such that yi=∑j=1kxjxi
即按比例将结果转化为概率的形式,且总和为 1 1 1
因此得到的 y i y_{i} yi有时也会写为 P ( y = i ∣ x ) P(y=i | x) P(y=i∣x)
反向传播
在训练模型过程中,我们会将样本集丢进初始化的模型中,得到预测值,通过预测值与标签(真实值)的差异来调整模型;在神经网络中也是如此。我们这里采用梯度下降的方式,且假定损失函数为均方误差,前向传播的过程如下:
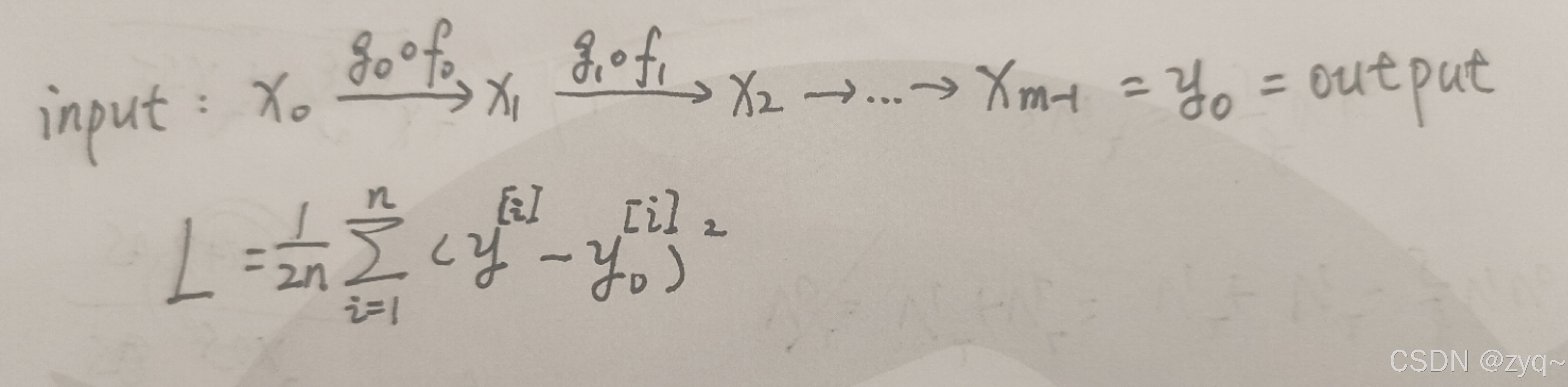
于是,根据梯度下降,有:
w j ( i ) = w j ( i ) − α δ L δ w j ( i ) w^{(i)}_{j} = w^{(i)}_{j} - \alpha \frac{\delta L}{\delta w^{(i)}_{j}} wj(i)=wj(i)−αδwj(i)δL
b j ( i ) = w j ( i ) − α δ L δ b j ( i ) b^{(i)}_{j} = w^{(i)}_{j} - \alpha \frac{\delta L}{\delta b^{(i)}_{j}} bj(i)=wj(i)−αδbj(i)δL
其中 α \alpha α为学习率, δ \delta δ是偏导,回顾一下每个神经元的运算:
z j ( i ) = f j ( i ) ( x ( i ) ) = w j ( i ) ⋅ x ( i ) + b j ( i ) z^{(i)}_{j} = f^{(i)}_{j}(x^{(i)}) = w^{(i)}_{j} \cdot x^{(i)} + b^{(i)}_{j} zj(i)=fj(i)(x(i))=wj(i)⋅x(i)+bj(i)
x j ( i + 1 ) = g ( z j ( i ) ) x^{(i+1)}_{j} = g(z^{(i)}_{j}) xj(i+1)=g(zj(i)),其中假设每个神经元用的都是g为 s i g m o i d sigmoid sigmoid函数,不作区分
应用链式法则:
δ L δ w j ( i ) = δ L δ x j ( i + 1 ) ∗ δ x j ( i + 1 ) δ z j ( i ) ∗ δ z j ( i ) δ w j ( i ) \frac{\delta L}{\delta w^{(i)}_{j}}=\frac{\delta L}{\delta x^{(i+1)}_{j}}*\frac{\delta x^{(i+1)}_{j}}{\delta z^{(i)}_{j}}*\frac{\delta z^{(i)}_{j}}{\delta w^{(i)}_{j}} δwj(i)δL=δxj(i+1)δL∗δzj(i)δxj(i+1)∗δwj(i)δzj(i)
= δ L δ x j ( i + 1 ) ∗ x j ( i + 1 ) ∗ ( 1 − x j ( i + 1 ) ) ∗ x j ( i ) \ \ \ \ \ \ \ \ \ =\frac{\delta L}{\delta x^{(i+1)}_{j}}*x^{(i+1)}_{j}*(1-x^{(i+1)}_{j})*x^{(i)}_{j} =δxj(i+1)δL∗xj(i+1)∗(1−xj(i+1))∗xj(i)
δ L δ b j ( i ) = δ L δ x j ( i + 1 ) ∗ δ x j ( i + 1 ) δ z j ( i ) ∗ δ z j ( i ) δ b j ( i ) \frac{\delta L}{\delta b^{(i)}_{j}}=\frac{\delta L}{\delta x^{(i+1)}_{j}}*\frac{\delta x^{(i+1)}_{j}}{\delta z^{(i)}_{j}}*\frac{\delta z^{(i)}_{j}}{\delta b^{(i)}_{j}} δbj(i)δL=δxj(i+1)δL∗δzj(i)δxj(i+1)∗δbj(i)δzj(i)
= δ L δ x j ( i + 1 ) ∗ x j ( i + 1 ) ∗ ( 1 − x j ( i + 1 ) ) \ \ \ \ \ \ \ \ \ =\frac{\delta L}{\delta x^{(i+1)}_{j}}*x^{(i+1)}_{j}*(1-x^{(i+1)}_{j}) =δxj(i+1)δL∗xj(i+1)∗(1−xj(i+1))
计算 δ L δ x j ( i ) \frac{\delta L}{\delta x^{(i)}_{j}} δxj(i)δL:
δ L δ x j ( i ) = δ L δ x j ( i + 1 ) ∗ δ x j ( i + 1 ) δ x j ( i ) \frac{\delta L}{\delta x^{(i)}_{j}} = \frac{\delta L}{\delta x^{(i+1)}_{j}} * \frac{\delta x^{(i+1)}_{j}}{\delta x^{(i)}_{j}} δxj(i)δL=δxj(i+1)δL∗δxj(i)δxj(i+1)
= δ L δ x j ( i + 1 ) ∗ x j ( i + 1 ) ∗ ( 1 − x j ( i + 1 ) ) ∗ w j ( i ) \ \ \ \ \ \ \ \ = \frac{\delta L}{\delta x^{(i+1)}_{j}} *x^{(i+1)}_{j}*(1-x^{(i+1)}_{j}) * w_{j}^{(i)} =δxj(i+1)δL∗xj(i+1)∗(1−xj(i+1))∗wj(i)
最后一层,这里 y y y是标签, y ′ y^{'} y′是预测值:
δ L δ x j ( m − 1 ) = δ L δ y j ′ = 1 n ∗ ( y j ′ − y j ) \frac{\delta L}{\delta x^{(m-1)}_{j}}=\frac{\delta L}{\delta y^{'}_{j}}=\frac{1}{n}*(y^{'}_{j}-y_{j}) δxj(m−1)δL=δyj′δL=n1∗(yj′−yj)
使用归纳(反向递推),即可得到 δ L δ x j ( i ) \frac{\delta L}{\delta x^{(i)}_{j}} δxj(i)δL
Q1: 为什么要用向量
因为电脑在处理向量或矩阵时能进行批量运算,在计算数量级很大时能显著节约训练时间。
Q2: 不用激活函数会发生什么
如果不用激活函数,意味着每一个节点都是进行线性变化,而线性变化的复合依然是线性变化,故再多的神经元也无法拟合出更好的结果。
相关文章:
【自学笔记】神经网络(1)
文章目录 介绍模型结构层(Layer)神经元 前向传播反向传播Q1: 为什么要用向量Q2: 不用激活函数会发生什么 介绍 我们已经学习了简单的分类任务和回归任务,也认识了逻辑回归和正则化等技巧,已经可以搭建一个简单的神经网络模型了。 …...

c#————扩展方法
关键点: 定义扩展方法的类和方法必须是静态的: 扩展方法必须在一个静态类中定义。扩展方法本身也必须是静态的。第一个参数使用 this 关键字: 扩展方法的第一个参数指定要扩展的类型,并且在这个参数前加上 this 关键字。这个参数…...
资料汇总)
前向-后向卡尔曼滤波器(Forward-Backward Kalman Filter)资料汇总
《卡尔曼滤波引出的RTS平滑》参考位置2《卡尔曼滤波系列——(六)卡尔曼平滑》《关于卡尔曼滤波和卡尔曼平滑关系的理解》——有m语言例程《Forward Backwards Kalman Filter》——Matlab软件《卡尔曼滤波与隐马尔可夫模型》...
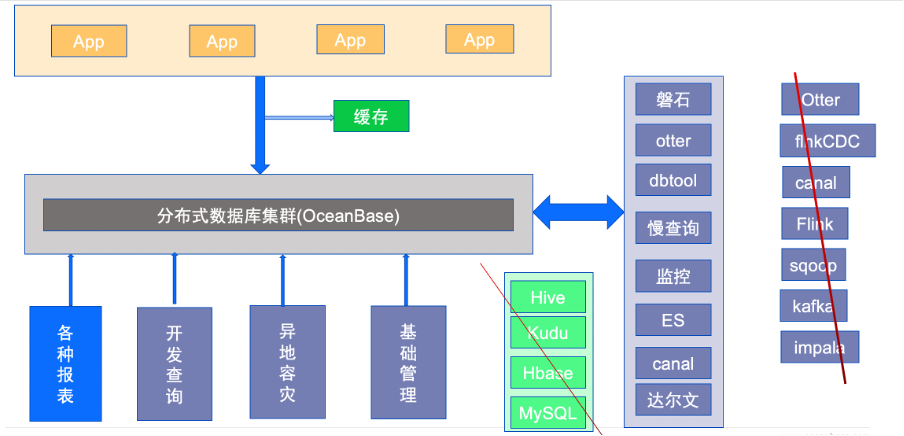
云集电商:如何通过 OceanBase 实现降本 87.5%|OceanBase案例
云集电商,一家聚焦于社交电商的电商公司,专注于‘精选’理念,致力于为会员提供超高性价比的全品类精选商品,以“批发价”让亿万消费者买到质量可靠的商品。面对近年来外部环境的变化,公司对成本控制提出了更高要求&…...

详解Rust标准库:BTreeMap
std::collections::BTreeMap定义 B树也称B-树,注意不是减号,是一棵多路平衡查找树;理论上,二叉搜索树 (BST) 是最佳的选择排序映射,但是每次查找时层数越多I/O次数越多,B 树使每个节…...

.NET WPF CommunityToolkit.Mvvm框架
文章目录 .NET WPF CommunityToolkit.Mvvm框架1 源生成器1.1 ObservablePropertyAttribute & RelayCommandAttribute1.2 INotifyPropertyChangedAttribute 2 可观测对象2.1 ObservableValidator2.2 ObservableRecipient .NET WPF CommunityToolkit.Mvvm框架 1 源生成器 1…...
微信小程序使用阿里巴巴矢量图标库正确姿势
1、打开官网:https://www.iconfont.cn/,把整理好的图标下载解压。 2、由于微信小程序不支持直接在wxss中引入.ttf/.woff/.woff2(在开发工具生效,手机不生效)。我们需要对下载的文件进一步处理。 eot:IE系列…...

【K8S问题系列 |1 】Kubernetes 中 NodePort 类型的 Service 无法访问【已解决】
在 Kubernetes 中,NodePort 类型的 Service 允许用户通过每个节点的 IP 地址和指定的端口访问应用程序。如果 NodePort 类型的 Service 无法通过节点的 IP 地址和指定端口进行访问,可能会导致用户无法访问应用。本文将详细分析该问题的常见原因及其解决方…...

Java基础Day-Thirteen
Java字符串 String类 创建String对象的方法 方法一:创建一个字符串对象imooc,名为s1 String s1"imooc"; 方法二:创建一个空字符串对象,名为s2 String s2new String(); 方法三:创建一个字符串对象imooc&a…...
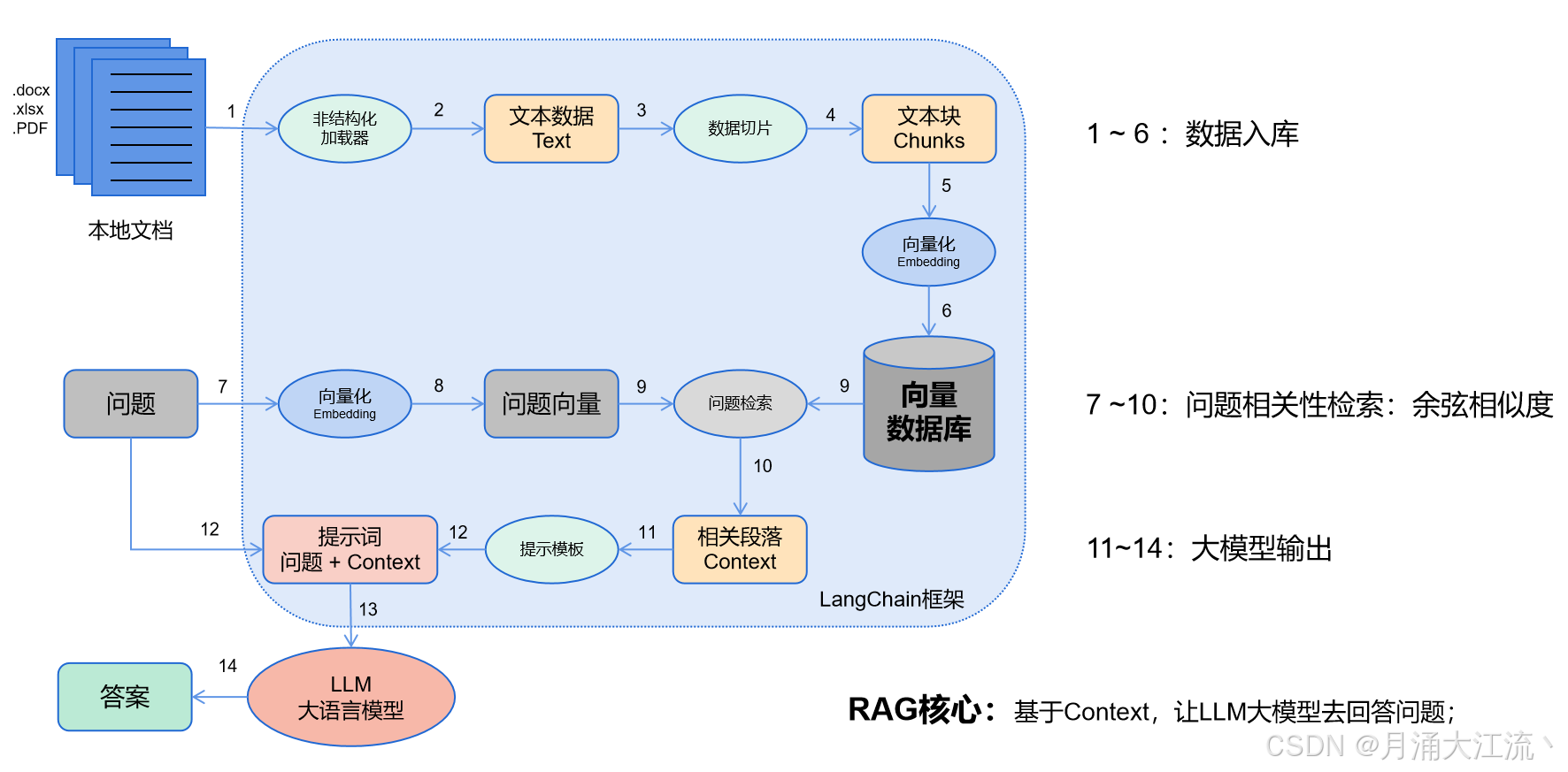
LangChain实际应用
1、LangChain与RAG检索增强生成技术 LangChain是个开源框架,可以将大语言模型与本地数据源相结合,该框架目前以Python或JavaScript包的形式提供; 大语言模型:可以是GPT-4或HuggingFace的模型;本地数据源:…...

【数据结构】哈希/散列表
目录 一、哈希表的概念二、哈希冲突2.1 冲突概念2.2 冲突避免2.2.1 方式一哈希函数设计2.2.2 方式二负载因子调节 2.3 冲突解决2.3.1 闭散列2.3.2 开散列(哈希桶) 2.4 性能分析 三、实现简单hash桶3.1 内部类与成员变量3.2 插入3.3 获取value值3.4 总代码…...
flutter 项目初建碰到的控制台报错无法启动问题
在第一次运行flutter时,会碰见一直卡在Runing Gradle task assembleDebug的问题。其实出现这个问题的原因有两个。 一:如果你flutter -doctor 检测都很ok,而且环境配置都很正确,那么大概率就是需要多等一会,少则几十分…...

Java字符串深度解析:String的实现、常量池与性能优化
引言 在Java编程中,字符串操作是最常见的任务之一。String 类在 Java 中有着独特的实现和特性,理解其背后的原理对于编写高效、安全的代码至关重要。本文将深入探讨 String 的实现机制、字符串常量池、不可变性的优点,以及 String、StringBu…...

leetcode 2043.简易银行系统
1.题目要求: 示例: 输入: ["Bank", "withdraw", "transfer", "deposit", "transfer", "withdraw"] [[[10, 100, 20, 50, 30]], [3, 10], [5, 1, 20], [5, 20], [3, 4, 15], [10, 50]] 输出ÿ…...
框架的文物管理系统)
基于SSM(Spring + Spring MVC + MyBatis)框架的文物管理系统
基于SSM(Spring Spring MVC MyBatis)框架的文物管理系统是一个综合性的Web应用程序,用于管理和保护文物资源。下面我将提供一个详细的案例程序概述,包括主要的功能模块和技术栈介绍。 项目概述 功能需求 用户管理:…...

yakit中的规则详细解释
官方文档 序列前置知识之高级配置 | Yak Program Language 本文章多以编写yaml模版的视角来解释 规则一览 匹配器 在编写yaml中会使用到这里两个东西 点击添加会在返回包的右下角出现匹配器 上面有三个过滤器模式,官方解释 丢弃:丢弃模式会在符合匹配…...

[c语言]strcmp函数的使用和模拟实现
1.strcmp函数的使用 int strcmp ( const char * str1, const char * str2 ); 如果 str1 小于 str2,返回一个负值。如果 str1 等于 str2,返回 0。如果 str1 大于 str2,返回一个正值。 实例: #include <stdio.h> #include &…...

如何把子组件的v-model修改数据,进行接收然后定义数据格式,子传父的实现
在 Vue 中,实现子组件通过 v-model 向父组件传递数据并接收后进行格式化,可以按照以下步骤来封装和实现: 步骤 1: 子组件实现 v-model 子组件需要定义一个 props 来接收 v-model 的值,并通过 emit 方法发出更新事件。 <!-- …...

linux dpkg 查看 安装 卸载 .deb
1、安装 sudo dpkg -i google-chrome-stable.deb # 如果您在安装过程中或安装和启动程序后遇到任何依赖项错误, # 您可以使用以下apt 命令使用-f标志解析和安装依赖项,该标志告诉程序修复损坏的依赖项。 # -y 表示自动回答“yes”,在安装…...

【算法】递归+深搜:105.从前序与中序遍历序列构造二叉树
目录 1、题目链接 2、题目介绍 3、解法 函数头-----找出重复子问题 函数体---解决子问题 4、代码 1、题目链接 105.从前序与中序遍历序列构造二叉树. - 力扣(LeetCode) 2、题目介绍 3、解法 前序遍历性质: 节点按照 [ 根节点 …...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

SpringAI实战:ChatModel智能对话全解
一、引言:Spring AI 与 Chat Model 的核心价值 🚀 在 Java 生态中集成大模型能力,Spring AI 提供了高效的解决方案 🤖。其中 Chat Model 作为核心交互组件,通过标准化接口简化了与大语言模型(LLM࿰…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...
