unity3d————四元数概念
一、定义与表示
四元数是由一个实数部分和三个虚数部分组成,通常表示为q = w + xi + yj + zk,其中w是实数,x、y、z是实数系数,i、j、k是虚数单位,满足以下关系:
- i² = j² = k² = -1
- ij = k,ji = -k
- jk = i,kj = -i
- ki = j,ik = -j
四元数也可以表示为q = [w, v],其中v = (x, y, z)是矢量,w是标量。虽然v是矢量,但它不能简单地理解为3D空间的矢量,而是在4维空间中的矢量。
二、几何意义与旋转
四元数中的i、j、k可以理解为一种旋转,其中:
- i旋转代表Z轴与Y轴相交平面中Z轴正向向Y轴正向的旋转。
- j旋转代表X轴与Z轴相交平面中X轴正向向Z轴正向的旋转。
- k旋转代表Y轴与X轴相交平面中Y轴正向向X轴正向的旋转。
- -i、-j、-k分别代表i、j、k旋转的反向旋转。
因此,四元数可以用来描述一个旋转轴和一个旋转角度。具体来说,一个四元数q可以执行一个旋转,将空间中的一个点P绕着单位向量轴u旋转θ角度。这个旋转可以通过将点P扩展到四元数空间,然后应用四元数乘法p' = qpq-1是q的共轭四元数。
三、性质与运算
四元数具有一些独特的性质和运算规则,包括:
- 模:四元数的模定义为|q| = √(w² + x² + y² + z²),它表示四元数到原点的距离。
- 共轭四元数:四元数的共轭定义为q* = w - xi - yj - zk。共轭四元数在旋转计算中起到关键作用。
- 逆四元数:四元数的逆定义为q^-1 = q* / |q|²。只有当四元数为单位四元数(即模为1的四元数)时,其逆才等于其共轭。
- 乘法:四元数的乘法不满足交换律,但满足结合律和分配律。四元数乘法的结果仍然是一个四元数,且可以用来合并旋转。
四、应用
四元数在计算机图形学、机器人学、航空航天等领域有广泛应用。与传统的欧拉角或旋转矩阵相比,四元数提供了一种更稳定、更高效的方式来处理三维旋转。它们可以避免欧拉角存在的万向锁(Gimbal Lock)问题,并且在进行多次旋转运算时不会积攒误差。此外,四元数还非常适合于旋转的插值计算,在动画和飞行模拟等领域有广泛应用。
五、总结
综上所述,四元数是一种在三维空间中表示旋转的数学结构,由实数部分和三个虚数部分组成。它们具有独特的性质和运算规则,并广泛应用于计算机图形学、机器人学等领域。四元数的引入为三维旋转的表示和处理提供了新的思路和方法。
上面概念大家大概看一下了解就行,想要深入了解可以自己查询相关数学知识,接下来就是unity3d部分,我们直接上代码:
public class siyuanshu : MonoBehaviour
{void Start(){//创建一个四元数Quaternion q = Quaternion.AngleAxis(60, Vector3.right);//创建一个游戏对象 把四元数赋值给他GameObject obj = GameObject.CreatePrimitive(PrimitiveType.Cube);obj.transform.rotation = q;}
}运行结果:



-
创建一个四元数:
Quaternion q = Quaternion.AngleAxis(60, Vector3.right);这行代码创建了一个四元数
q,它表示一个围绕X轴(在Unity中,Vector3.right代表X轴的正方向)旋转60度的旋转。Quaternion.AngleAxis方法接受两个参数:一个是旋转的角度(以度为单位),另一个是旋转轴(一个Vector3向量)。这里,旋转轴是X轴,角度是60度。 -
创建一个游戏对象:
GameObject obj = GameObject.CreatePrimitive(PrimitiveType.Cube);这行代码使用
GameObject.CreatePrimitive方法创建了一个新的游戏对象,这个对象是一个立方体(PrimitiveType.Cube)。新创建的游戏对象会被自动添加到当前的Unity场景中,并且其位置默认在场景的原点(0,0,0)。 -
把四元数赋值给游戏对象的旋转:
obj.transform.rotation = q;这行代码将之前创建的四元数
q赋值给新创建的立方体游戏对象的transform.rotation属性。这意味着立方体将会被旋转,以匹配四元数q所表示的旋转。具体来说,立方体将会围绕其自身的X轴旋转60度。
API讲解:
public static Quaternion AngleAxis(float angle, Vector3 axis);
参数:
angle(float):要旋转的角度,以度为单位。正值表示按顺时针方向旋转(根据右手定则),负值表示按逆时针方向旋转。axis(Vector3):旋转所围绕的轴,该轴应该是一个归一化(即长度为1)的向量。如果提供的轴不是归一化的,Unity 会自动将其归一化,但这可能会引入一些微小的数值误差,因此最好自己预先归一化轴。
返回值:
- 返回一个
Quaternion,表示围绕指定轴旋转指定角度的旋转。
用法:
Quaternion.AngleAxis常用于创建表示特定旋转的四元数,这些旋转可以随后应用于游戏对象(GameObject)的Transform组件,以改变其方向。
public static GameObject CreatePrimitive(PrimitiveType type);
参数:
type(PrimitiveType):这是一个枚举类型,指定了要创建的基本几何体的类型。PrimitiveType枚举包含了多种几何体类型,如Cube(立方体)、Sphere(球体)、Cylinder(圆柱体)、Capsule(胶囊体)、Plane(平面)、Quad(四边形)等。
返回值:
- 返回一个
GameObject,它是新创建的基本几何体的实例。这个GameObject包含了表示几何体的MeshRenderer组件和MeshFilter组件,以及用于定位、旋转和缩放的Transform组件。
用法:
CreatePrimitive方法通常用于在脚本中动态添加几何体到场景中,特别是在需要根据游戏逻辑动态生成内容的情况下。
public Quaternion rotation { get; set; }
rotation属性的特点:
-
类型:
Quaternion,这是一个用于表示三维旋转的四元数结构。 -
可读写:你可以通过
transform.rotation来获取当前游戏对象的旋转状态,也可以通过给它赋值来设置新的旋转。 -
影响:改变
transform.rotation的值会立即影响游戏对象在场景中的方向。 -
避免万向锁:与欧拉角(Euler angles)相比,四元数在表示旋转时不会遇到万向锁(gimbal lock)的问题,这使得它成为三维旋转的理想选择。
-
组合旋转:四元数支持乘法运算,这意味着你可以将多个旋转组合在一起,得到一个总的旋转效果。例如,
transform.rotation = rotationA * rotationB;会将rotationB应用到rotationA上,得到一个新的旋转,并将其赋值给transform.rotation。 -
插值:在动画和过渡效果中,四元数插值(如
Quaternion.Lerp和Quaternion.Slerp)允许你平滑地在两个旋转之间过渡。
相关文章:

unity3d————四元数概念
一、定义与表示 四元数是由一个实数部分和三个虚数部分组成,通常表示为q w xi yj zk,其中w是实数,x、y、z是实数系数,i、j、k是虚数单位,满足以下关系: i j k -1ij k,ji -kjk i&…...

spring相关的面试题
Spring 框架是 Java 开发中最常用的框架之一,因此在面试中经常会被问到与 Spring 相关的问题。以下是一些常见的 Spring 面试题及其答案。 基础概念 什么是 Spring 框架? Spring 框架是一个开源的 Java 平台,用于构建企业级应用程序。它提供…...

STM32外设之SPI的介绍
### STM32外设之SPI的介绍 SPI(Serial Peripheral Interface)是一种高速的,全双工,同步的通信总线,主要用于EEPROM、FLASH、实时时钟、AD转换器等外设的通信。SPI通信只需要四根线,节约了芯片的管脚&#x…...

二十三、Mysql8.0高可用集群架构实战
文章目录 一、MySQL InnoDB Cluster1、基本概述2、集群架构3、搭建一主两从InnoDB集群3.1、 安装3个数据库实例3.2、安装mysqlrouter和安装mysqlshell3.2.1、安装mysql-router3.2.2、安装mysql-shell 3.3、InnoDB Cluster 初始化3.3.1、参数及权限配置预需求检测3.3.2、初始化I…...

docker file 精简规则
在编写 Dockerfile 时,精简规则不仅有助于减小镜像大小,还能提高构建速度和可维护性。以下是一些常见的精简 Dockerfile 规则: 1. 尽量合并 RUN 指令 每个 RUN 指令会产生一个新的镜像层,因此多个命令可以合并为一个 RUN 指令&a…...

前端加密方式详解与选择指南
在当今数字化时代,前端数据安全的重要性日益凸显。本文将深入探讨前端加密的多种方式,为你提供选择适合项目加密方式的实用策略,并分享一些实际案例及相应代码。 一、前端加密方式汇总 (一)HTTPS 加密 HTTPS 是在 H…...

【React】条件渲染——逻辑与运算符
条件渲染——逻辑与&&运算符 你会遇到的另一个常见的快捷表达式是 JavaScript 逻辑与(&&)运算符。在 React 组件里,通常用在当条件成立时,你想渲染一些 JSX,或者不做任何渲染。 function Item({ nam…...

MATLAB中eig函数用法
目录 语法 说明 示例 矩阵特征值 矩阵的特征值和特征向量 排序的特征值和特征向量 左特征向量 不可对角化(亏损)矩阵的特征值 广义特征值 病态矩阵使用 QZ 算法得出广义特征值 一个矩阵为奇异矩阵的广义特征值 eig函数的功能是求取矩阵特征值…...

Chrome(谷歌浏览器中文版)下载安装(Windows 11)
目录 Chrome_10_30工具下载安装 Chrome_10_30 工具 系统:Windows 11 下载 官网:https://chrome.google-zh.com/,点击立即下载 下载完成(已经下过一遍所以点了取消) 安装 解压,打开安装包 点击下一步…...

Linux 配置JDK
文章目录 一、下载Oracle-JDK1.1、如何正确的下载JDK 二、配置JDK环境变量2.1 环境变量配置2.1.1、修改vim /etc/profile 添加jdk的路径 一、下载Oracle-JDK 1.1、如何正确的下载JDK 首先我要安装的是oracle-jdk,这个时候什么地方都不要去,就去oracle的…...

目前主流的人工智能学习框架有哪些?
随着人工智能(AI)技术的蓬勃发展,越来越多的AI学习框架相继推出,成为开发者、研究人员和企业构建机器学习(ML)和深度学习(DL)模型的首选工具。AI学习框架不仅提供了丰富的工具库和函…...

100种算法【Python版】第57篇——贝叶斯优化算法
本文目录 1 算法说明2 贝叶斯优化的步骤3 算法应用1:目标函数最大值4 算法应用2:确定最佳试验参数1 算法说明 贝叶斯优化是一种旨在优化黑箱目标函数的策略,通常适用于评估代价高昂或时间消耗长的函数。它利用贝叶斯统计方法来构建目标函数的概率模型,进而指导下一步的采样…...

在Ubuntu 上实现 JAR 包的自启动
在 Ubuntu 上实现 JAR 包的自启动,可以通过以下几种方法: 方法一:使用 systemd 创建一个服务文件: 在 /etc/systemd/system/ 目录下创建一个新的服务文件,例如 myapp.service: sudo nano /etc/systemd/sys…...

【智能算法应用】哈里斯鹰算法优化二维栅格路径规划问题
摘要 本文研究了基于哈里斯鹰优化算法(Harris Hawks Optimization, HHO)的二维栅格路径规划方法。HHO算法模拟哈里斯鹰的猎食行为,通过迭代搜索过程找到从起点到终点的最优路径,避开栅格中的障碍物。实验结果表明,HHO…...

单品年销10亿!看麻辣王子是如何布局软文营销为品牌赋能的?
说到辣条,除了大家熟知的卫龙之外,还有一个不得不提的品牌就是——麻辣王子。 作为来自辣条发源地湖南平江的老牌辣条企业,麻辣王子近几年通过打造品牌,积极破圈,2023年凭借一款单品狂揽超10亿年销售额,稳…...

【开源免费】基于SpringBoot+Vue.JS医院管理系统(JAVA毕业设计)
博主说明:本文项目编号 T 062 ,文末自助获取源码 \color{red}{T062,文末自助获取源码} T062,文末自助获取源码 目录 一、系统介绍二、演示录屏三、启动教程四、功能截图五、文案资料5.1 选题背景5.2 国内外研究现状5.3 可行性分析…...

C++:模拟实现STL的string
目录 一.实现string类 1.string的构造及析构 2.string类的遍历 3.string类的插入和删除 4.string类的空间处理 5.string类的查找 6.string类的输出和输入 7.string类的常用判断 二.整体代码 1.string.h 2.string.cpp 一.实现string类 在前一节中我们了解了STL中stri…...

【Python TensorFlow】入门到精通
TensorFlow 是一个开源的机器学习框架,由 Google 开发,广泛应用于机器学习和深度学习领域。本篇将详细介绍 TensorFlow 的基础知识,并通过一系列示例来帮助读者从入门到精通 TensorFlow 的使用。 1. TensorFlow 简介 1.1 什么是 TensorFlow…...

数据结构:七种排序及总结
文章目录 排序一插入排序1直接插入排序2希尔排序二选择排序3直接选择排序4堆排序三 交换排序5冒泡排序6快速排序四 归并排序7归并排序源码 排序 我们数据结构常见的排序有四大种,四大种又分为七小种,如图所示 排序:所谓排序,就是…...
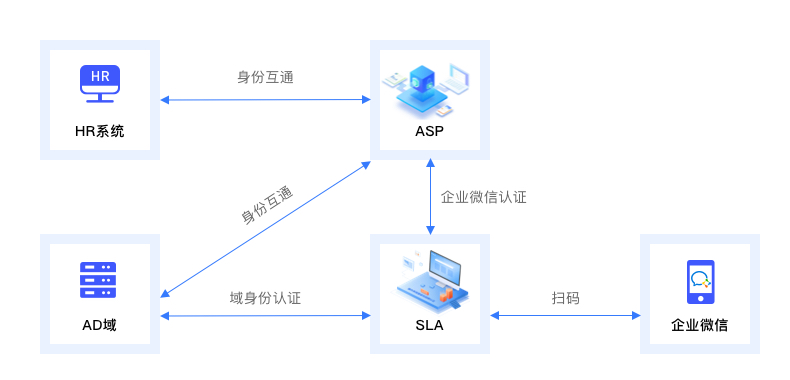
【安当产品应用案例100集】030-使用企业微信登录Windows,实现工作电脑与业务系统登录方式统一
随着越来越多的企业信息系统从intranet开放到internet,企业员工的办公接入方式也越发多样,信息系统面临的数据安全问题也呈现爆发的趋势。一些大企业,比如Google、Microsoft、Huawei有强大的开发能力、IT能力,可以构建出自己的零信…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...
