CPP贪心算法示例
设有n个正整数(n ≤ 20),将它们联接成一排,组成一个最大的多位整数。
例如:n=3时,3个整数13,312,343联接成的最大整数为:34331213
又如:n=4时,4个整数7,13,4,246联接成的最大整数为:7424613
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
string intToStr(int x)
{return to_string(x);//例如 12345 会变成 “12345”
}// 比较函数,用于确定两个数字拼接后的顺序
bool compare(const int& x, const int& y) {string xStr = intToStr(x);string yStr = intToStr(y);string xyStr = xStr + yStr;// + 运算符可以直接链接两个string类型函数string yxStr = yStr + xStr;return xyStr > yxStr; // 返回拼接后较大的那个顺序
}int main() {int n;cin >> n;vector<int> a(n);for (int i = 0; i < n; ++i) {cin >> a[i];}// 使用自定义的比较函数对向量进行排序sort(a.begin(), a.end(), compare);//注意这里只能用迭代器不能用sort(arr, arr + n, compare)// 输出排序后的结果for (size_t i = 0; i < a.size(); ++i) {cout << a[i];}cout << endl;return 0;
}相关文章:

CPP贪心算法示例
设有n个正整数(n ≤ 20),将它们联接成一排,组成一个最大的多位整数。 例如:n3时,3个整数13,312,343联接成的最大整数为:34331213 又如:n4时,4个整…...

GPT对NLP的冲击
让我来详细解释张俊林对GPT冲击NLP领域的分析: 中间任务(脚手架)的消失: 传统NLP中间任务: - 分词 - 词性标注 - 命名实体识别 - 句法分析 - 词向量学习为什么会消失: - GPT直接进行端到端学习 - 不需要人工定义的中间步骤 - 模…...

中值定理类证明题中对‘牛顿插值法’的应用
牛顿插值法是一种使用多项式插值的方法,它通过构造一个多项式来近似一组数据点。这种方法是由艾萨克牛顿提出的。牛顿插值法的一个优点是,当需要添加更多的数据点时,它不需要重新计算整个多项式,只需要对现有的多项式进行修改。...

HTMLCSS:3D 旋转卡片的炫酷动画
效果演示 这段代码是一个HTML和CSS的组合,用于创建一个具有3D效果的动画卡片。 HTML <div class"obj"><div class"objchild"><span class"inn6"><h3 class"text">我是谁?我在那<…...

Node.js 全栈开发进阶篇
🌈个人主页:前端青山 🔥系列专栏:node.js篇 🔖人终将被年少不可得之物困其一生 依旧青山,本期给大家带来node.js篇专栏内容:node.js- 全栈开发进阶篇 前言 大家好,我是青山。在上一篇文章中,…...

SQL语句-MySQL
数据定义声明 改变数据库语句 ALTER {DATABASE | SCHEMA} [db_name]alter_option ... ALTER {DATABASE | SCHEMA} db_nameUPGRADE DATA DIRECTORY NAMEalter_option: {[DEFAULT] CHARACTER SET [] charset_name| [DEFAULT] COLLATE [] collation_name } ALTER DATABASE使您能…...

Tencent Hunyuan3D
一、前言 腾讯于2024年11月5日正式开源了最新的MoE模型“混元Large”以及混元3D生成大模型“Hunyuan3D-1.0”,支持企业及开发者在精调、部署等不同场景下的使用需求。 GitHub - Tencent/Hunyuan3D-1 二、技术与原理 Hunyuan3D-1.0 是一款支持文本生成3D(…...

[ABC239E] Subtree K-th Max
[ABC239E] Subtree K-th Max 题面翻译 给定一棵 n n n 个节点的树,每个节点的权值为 x i x_i xi。 现有 Q Q Q 个询问,每个询问给定 v , k v,k v,k,求节点 v v v 的子树第 k k k 大的数。 0 ≤ x i ≤ 1 0 9 , 2 ≤ n ≤ 1 0 5 , …...
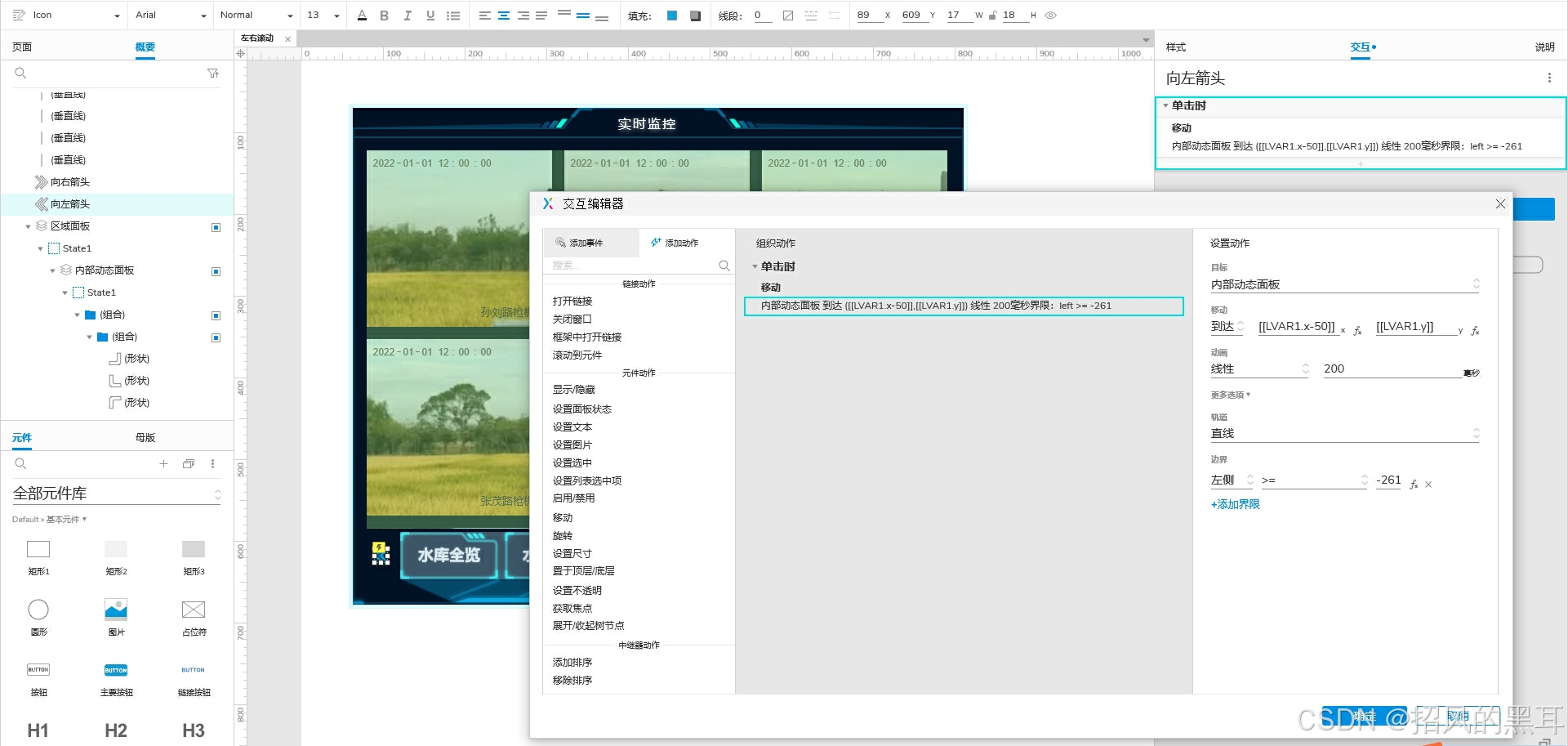
Axure设计之左右滚动组件教程(动态面板)
很多项目产品设计经常会遇到左右滚动的导航、图片展示、内容区域等,接下来我们用Axure来实现一下左右滚动的菜单导航。通过案例我们可以举一反三进行其他方式的滚动组件设计,如常见的上下滚动、翻页滚动等等。 一、效果展示: 1、点击“向左箭…...

善用Git LFS来降低模型文件对磁盘的占用
将讲一个实际的例子:对于模型文件,动辄就是好几个G,而有的仓库更是高达几十G,拉一个仓库到本地,稍不注意直接磁盘拉满都有可能。 比如:meta-llama-3.1-8b-instruct,拉到本地后发现居然占用了60G…...

Oracle RAC的thread
参考文档: Real Application Clusters Administration and Deployment Guide 3 Administering Database Instances and Cluster Databases Initialization Parameter Use in Oracle RAC Table 3-3 Initialization Parameters Specific to Oracle RAC THREAD Sp…...

如何创建备份设备以简化 SQL Server 备份过程?
SQL Server 中的备份设备是什么? 在 SQL Server 中,备份设备是用于存储备份数据的物理或逻辑介质。备份设备可以是文件、设备或其他存储介质。主要类型包括: 文件备份设备:通常是本地文件系统中的一个或多个文件。可以是 .bak 文…...

DeBiFormer实战:使用DeBiFormer实现图像分类任务(一)
摘要 一、论文介绍 研究背景:视觉Transformer在计算机视觉领域展现出巨大潜力,能够捕获长距离依赖关系,具有高并行性,有利于大型模型的训练和推理。现有问题:尽管大量研究设计了高效的注意力模式,但查询并…...

【go从零单排】迭代器(Iterators)
🌈Don’t worry , just coding! 内耗与overthinking只会削弱你的精力,虚度你的光阴,每天迈出一小步,回头时发现已经走了很远。 📗概念 在 Go 语言中,迭代器的实现通常不是通过语言内置的迭代器类型&#x…...

Java与HTML:构建静态网页
在Web开发领域,HTML是构建网页的基础标记语言,而Java作为一种强大的编程语言,也能够在创建HTML内容方面发挥重要作用。今天,我们就来探讨一下如何使用Java来制作一个不那么简单的静态网页。 一、项目准备 首先,我们需…...

软件测试:测试用例详解
🍅 点击文末小卡片,免费获取软件测试全套资料,资料在手,涨薪更快 一、通用测试用例八要素 1、用例编号; 2、测试项目; 3、测试标题; 4、重要级别; 5、预置…...

FreeSWITCH Ubuntu 18.04 源码编译
应朋友邀请,试了试 FreeSWITCH Ubuntu 18.04 源码编译,交的作业如下: #!/bin/bash####### Ubuntu 18.04 LTS ####### ARM64 ####### FreeSWITCH 1.10.12apt update && \ apt install -y --fix-missing git sed bison build-essentia…...

spring—boot(整合redis)
整合redis 第一步导入数据源 <!--redis--> <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-data-redis</artifactId> </dependency> RedisConfig(默认有RedisTemplate&#…...

Python 包镜像源
阿里云、清华大学和豆瓣之外,还有许多其他的 Python 包镜像源。下面是更新后的代码,增加了更多常用的镜像源,如华为云、腾讯云等 import tkinter as tk from tkinter import messagebox import os# 定义 pip 配置文件路径 pip_config_file …...

Sigrity SPEED2000 Power Ground Noise Simulation模式如何进行电源阻抗仿真分析操作指导(一)-无电容
Sigrity SPEED2000 Power Ground Noise Simulation模式如何进行电源阻抗仿真分析操作指导(一)-无电容 Sigrity Power Ground Noise Simulation模式同样可以用来观测电源网络的自阻抗,以下图为例进行说明 2D 视图 3D view 本例要观测的是U17端口处的自阻抗࿰…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...
