力扣11.5
1035. 不相交的线
在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。
现在,可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线,这些直线需要同时满足:
nums1[i] == nums2[j]- 且绘制的直线不与任何其他连线(非水平线)相交。
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
以这种方法绘制线条,并返回可以绘制的最大连线数。
数据范围
1 <= nums1.length, nums2.length <= 5001 <= nums1[i], nums2[j] <= 2000
分析
实际就是求最长公共子序列
代码
class Solution {
public: const static int N = 505;int dp[N][N];int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {int n = nums1.size(), m = nums2.size();for(int i = 0; i < n; i ++ ) {for(int j = 0; j < m; j ++ ) {dp[i + 1][j + 1] = max(dp[i][j + 1], dp[i + 1][j]);if(nums1[i] == nums2[j]) dp[i + 1][j + 1] = max(dp[i + 1][j + 1], dp[i][j] + 1);}}return dp[n][m];}
};
1458. 两个子序列的最大点积
给你两个数组 nums1 和 nums2 。
请你返回 nums1 和 nums2 中两个长度相同的 非空 子序列的最大点积。
数组的非空子序列是通过删除原数组中某些元素(可能一个也不删除)后剩余数字组成的序列,但不能改变数字间相对顺序。比方说,[2,3,5] 是 [1,2,3,4,5] 的一个子序列而 [1,5,3] 不是。
数据范围
1 <= nums1.length, nums2.length <= 500-1000 <= nums1[i], nums2[i] <= 100
分析
最长公共子序列的变式,令dp[i][j]表示nums1的前i个数和nums2的前j个数所能构成的点积最大值,接下来考虑nums1[i]和nums2[j]是否选择
- 若nums1[i]*nums2[j]<0
- 只选择nums1[i],dp[i][j]=dp[i][j-1]
- 只选择nums2[j],dp[i][j]=dp[i-1][j]
- 这里不能都不选,因为题目规定是非空子序列,还有第三种情况,dp[i][j]=nums1[i]*nums2[j]
- 若nums1[i]*nums2[j]>0
- dp[i][j]=dp[i-1][j-1]+nums1[i]*nums2[j]
代码
class Solution {
public:const static int N = 505;int dp[N][N];int maxDotProduct(vector<int>& nums1, vector<int>& nums2) {int n = nums1.size(), m = nums2.size();memset(dp, -0x3f, sizeof(dp));for(int i = 0; i < n; i ++ ) {for(int j = 0; j < m; j ++ ) {dp[i + 1][j + 1] = max(nums1[i] * nums2[j], max(dp[i][j + 1], dp[i + 1][j]));if(nums1[i] * nums2[j] >= 0) {dp[i + 1][j + 1] = max(dp[i + 1][j + 1], dp[i][j] + nums1[i] * nums2[j]);} }}return dp[n][m];}
};
224. 基本计算器
给你一个字符串表达式 s ,请你实现一个基本计算器来计算并返回它的值。
注意:不允许使用任何将字符串作为数学表达式计算的内置函数,比如 eval() 。
数据范围
1 <= s.length <= 3 * 105s 由数字、'+'、'-'、'('、')'、和 ' ' 组成s 表示一个有效的表达式'+' 不能用作一元运算(例如, "+1" 和 "+(2 + 3)" 无效)'-' 可以用作一元运算(即 "-1" 和 "-(2 + 3)" 是有效的)输入中不存在两个连续的操作符每个数字和运行的计算将适合于一个有符号的 32位 整数
分析
使用一个操作数栈和一个符号栈,先转换为后缀表达式,然后求解
**注意:**对于-a的处理是变成0-a的形式
代码
typedef long long LL;
class Solution {
public:const static int N = 3e5 + 5;int tt1 = -1, tt2 = -1;char stk[N];LL num[N];LL calculate(string s) {int start = 0;for(int i = start; i < s.size(); i ++ ) {if(s[i] == ' ') continue;if(s[i] == '(') stk[++ tt1] = s[i];else if(s[i] == ')') {int a = num[tt2];int b = num[tt2 - 1];int j = tt1;while(j != -1 && stk[j] != '(') {if(stk[j] == '+') num[-- tt2] = a + b;else if(stk[j] == '-') num[-- tt2] = b - a;j -- ;}tt1 = j - 1;} else if(s[i] >= '0' && s[i] <= '9') {LL tnum = 0;int j = i;while(s[j] >= '0' && s[j] <= '9') {tnum = tnum * 10 + s[j] - '0';j ++ ;}i = j - 1;num[++ tt2] = tnum;} else if(s[i] == '+' || s[i] == '-') {if(tt1 == -1 || stk[tt1] == '(') stk[++ tt1] = s[i];else {int a = num[tt2];int b = num[tt2 - 1];if(stk[tt1] == '+') num[-- tt2] = a + b;else num[-- tt2] = b - a;stk[tt1] = s[i];}if(s[i] == '-') {int j = i - 1;while(j >= 0) {if(s[j] == ' ') j -- ;if(s[j] == ')') j -- ;if(s[j] >= '0' && s[j] <= '9') break;if(s[j] == '(') break;}if(j < 0 || s[j] == '(') {num[++ tt2] = 0;}}}}if(tt1 != -1) {for(int i = tt2; i >= 0; i -- ) {int a = num[tt2];int b = num[tt2 - 1];if(stk[i] == '+') num[-- tt2] = a + b;else if(stk[i] == '-') num[-- tt2] = b - a;}}return num[0];}
};
1092. 最短公共超序列
给你两个字符串 str1 和 str2,返回同时以 str1 和 str2 作为 子序列 的最短字符串。如果答案不止一个,则可以返回满足条件的 任意一个 答案。
如果从字符串 t 中删除一些字符(也可能不删除),可以得到字符串 s ,那么 s 就是 t 的一个子序列。
数据范围
1 <= str1.length, str2.length <= 1000str1 和 str2 都由小写英文字母组成。
分析
令dp[i][j]为包含str1的前i个字符和str2的前j个字符的最短字符串长度,最原始的dp做法是,用另一个dp数组dp2表示包含str1的前i个字符和str2的前j个字符的最短字符串,但这样内存会超,这道题可以通过路径追踪类似的方法得到最终的字符串
代码
typedef pair<pair<int, int>, char> PIIC;
class Solution {
public:const static int N = 1005;int dp[N][N];PIIC last[N][N];string shortestCommonSupersequence(string str1, string str2) {int n = str1.size();int m = str2.size();memset(dp, 0x3f, sizeof(dp));dp[0][0] = 0;for(int i = 1; i <= m; i ++ ) {dp[0][i] = i;last[0][i] = {{0, i - 1}, str2[i - 1]};}for(int i = 1; i <= n; i ++ ) {dp[i][0] = i;last[i][0] = {{i - 1, 0}, str1[i - 1]};}for(int i = 0; i < n; i ++ ) {for(int j = 0; j < m; j ++ ) {if(dp[i + 1][j + 1] > dp[i][j + 1] + 1) {dp[i + 1][j + 1] = dp[i][j + 1] + 1;last[i + 1][j + 1] = {{i, j + 1}, str1[i]};} if(dp[i + 1][j + 1] > dp[i + 1][j] + 1) {dp[i + 1][j + 1] = dp[i + 1][j] + 1;last[i + 1][j + 1] = {{i + 1, j}, str2[j]};}if(str1[i] == str2[j]) {if(dp[i + 1][j + 1] > dp[i][j] + 1) {dp[i + 1][j + 1] = dp[i][j] + 1;last[i + 1][j + 1] = {{i, j}, str1[i]};}}}}string res = "";PIIC now = last[n][m];while(now.first.first != 0 || now.first.second != 0) {res = now.second + res;PIIC tmp = now;now = last[now.first.first][now.first.second];if(now.first.first == 0 && now.first.second == 0) {if(tmp.first.second != 0) res = str2[0] + res;else res = str1[0] + res;}}return res;}
};
相关文章:

力扣11.5
1035. 不相交的线 在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。 现在,可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线,这些直线需要同时满足: nums1[i] nums2[j]且绘制的直线不与任何其他连线(非…...

arkUI:层叠布局(Stack)
arkUI:层叠布局(Stack) 1 主要内容说明2 相关内容2.1 层叠布局(Stack)2.1.1 源码1的相关说明2.1.2 源码1 (层叠布局)2.1.3 源码1运行效果2.1.3.1 当alignContent: Alignment.Bottom2.1.3.2 当al…...

【LeetCode】【算法】221. 最大正方形
LeetCode 221. 最大正方形 题目描述 在一个由 ‘0’ 和 ‘1’ 组成的二维矩阵内,找到只包含 ‘1’ 的最大正方形,并返回其面积。 思路 思路:动态规划。初始化时,第0列和第0行,若nums[i][j]1则dp[i][j]初始化为1&am…...

怎麼解除IP阻止和封禁?
IP地址被阻止的原因 安全問題如果有人使用 IP 地址試圖侵入某個網站或導致其他安全問題,則可能會禁止該 IP 以保護該網站。濫用或垃圾郵件如果IP地址發送過多垃圾郵件、發佈不當內容或濫用網站服務,則可能會被禁止,以保持網站清潔和友好。違…...

O-RAN Fronthual CU/Sync/Mgmt 平面和协议栈
O-RAN Fronthual CU/Sync/Mgmt 平面和协议栈 O-RAN Fronthual CU/Sync/Mgmt 平面和协议栈O-RAN前端O-RAN 前传平面C-Plane(控制平面):控制平面消息定义数据传输、波束形成等所需的调度、协调。U-Plane(用户平面)&#…...

一招解决Mac没有剪切板历史记录的问题
使用Mac的朋友肯定都为Mac的剪切功能苦恼过,旧内容覆盖新内容,导致如果有内容需要重复输入的话,就需要一次一次的重复复制粘贴,非常麻烦 但其实Mac也能够有剪切板历史记录功能,iCopy,让你的Mac也能拥有剪切…...
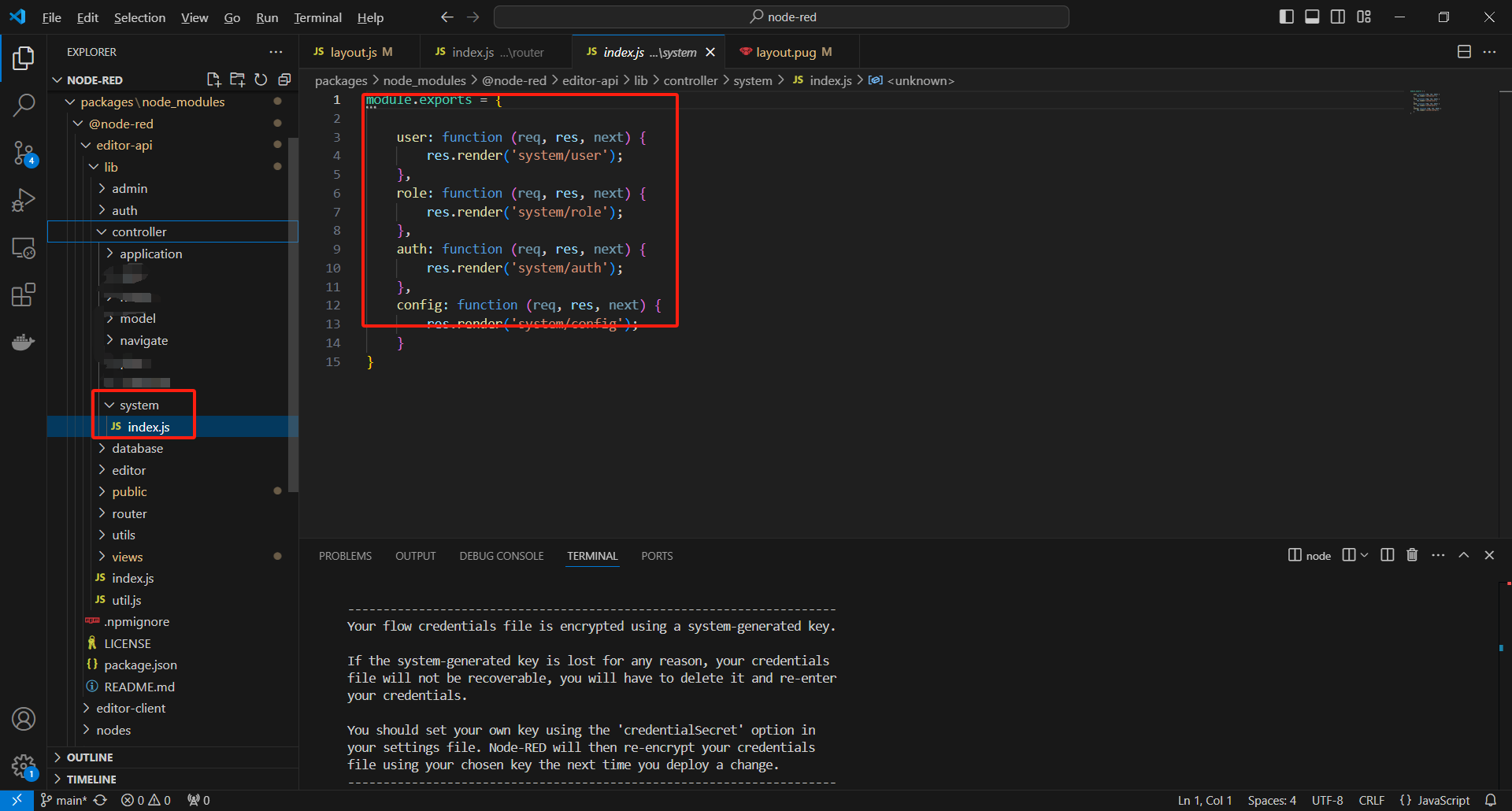
Node-Red二次开发:各目录结构说明及开发流程
node-red下载之前需要安装nodejs软件,然后设置环境变量; node-red下载之后,需要先安装依赖: 1. 安装依赖shell npm install # 或 yarn install 2. 运行shell npm run dev node-red的目录结构: node-red的前后端都是…...

论文阅读-Event-based Visible and Infrared Fusion via Multi-task Collaboration
一、前言 可见光图像与红外图像融合(VIF)通过结合热红外图像与可见光图像的丰富纹理,提供了一个全面可靠的场景描述。然而,传统的VIF系统可能在极端光照和高动态运动场景中捕获过曝或欠曝的图像,进而导致融合结果下降…...
Spring Boot2(Spring Boot 的Web开发 springMVC 请求处理 参数绑定 常用注解 数据传递 文件上传)
SpringBoot的web开发 静态资源映射规则 总结:只要静态资源放在类路径下: called /static (or /public or /resources or //METAINF/resources 一启动服务器就能访问到静态资源文件 springboot只需要将图片放在 static 下 就可以被访问到了 总结&…...

nginx中location模块中的root指令和alias指令区别
在 Nginx 配置中,location 模块用于定义如何处理特定请求路径。root 和 alias 是两个常用的指令,用于指定请求文件的位置,但它们有不同的行为。 root 指令 root 指令用于设置请求的根目录。当请求到来时,Nginx 会将请求的 URI 附…...

C++ 线程常见的实际场景解决方案
文章目录 一、主线程阻塞等待子线程返回1、代码示例2、代码改进 一、主线程阻塞等待子线程返回 主线程等待一个线程,此线程会开始连接一个服务器并循环读取服务器存储的值,主线程会阻塞直到连接服务器成功。因为如果不阻塞,可能上层业务刚开…...

Node.js——fs模块-文件删除
1、在Node.js中,我们可以使用unlink或unlinkSync来删除文件。 2、语法: fs.unlink(path,callback) fs.unlinkSync(path) 参数说明: path 文件路径 callback 操作后的回调函数 本文的分享到此结束,欢迎大家评论区一同讨论学…...

发布一个npm组件库包
Webpack 配置 (webpack.config.js) const path require(path); const MiniCssExtractPlugin require(mini-css-extract-plugin); const CssMinimizerPlugin require(css-minimizer-webpack-plugin); const TerserPlugin require(terser-webpack-plugin);module.exports {…...

处理PhotoShopCS5和CS6界面字体太小
处理PhotoShop CS6界面字体太小 背景:安装PhotoShop CS6后发现无法调大字体大小,特别是我的笔记本14寸的,显示的字体小到离谱。 百度好多什么降低该电脑分辨率,更改电脑的显示图标大小,或者PS里的首选项中的界面设置。…...

srs http-flv处理过程
目录 处理tcp请求,创建HttpConn 解析 http request创建consumer 读取consumer数据转封装为flv 处理tcp请求,创建HttpConn 调用堆栈如下: srs!SrsHttpConn::SrsHttpConn(ISrsHttpConnOwner*, ISrsProtocolReadWriter*, ISrsHttpServeMux*, std::__1::basic_string<ch…...

若Git子模块的远端地址发生了变化本地应该怎么调整
文章目录 前言git submodule 相关命令解决方案怎么保存子模块的版本呢总结 前言 这个问题复杂在既有Git又有子模块,本身Git的门槛就稍微高一点,再加上子模块的运用,一旦出现这种远端地址发生修改的情况会让人有些懵,不知道怎么处…...
docker运行code-servre并配置https通信
code-server 可以在浏览器中运行,使得开发者可以随时随地通过网络访问自己的开发环境,无需局限于某一台设备。只要有浏览器和网络连接,就可以继续编写代码和调试项目,非常适合远程办公和移动办公的需求。 由于每次启动code-serve…...

Linux 外设驱动 应用 4 触摸屏实验
触摸屏实验 1 触摸屏介绍1.1 基本应用介绍1.2 触摸屏工作原理介绍1.3 硬件介绍 2 应用代码编写2.1 找到输入设备2.2 打开驱动2.3 驱动查询应用2.4 应用结果 1 触摸屏介绍 1.1 基本应用介绍 LCD 显示屏包括显示屏和触摸屏,上层的是触摸屏,下层是显示屏。…...
Python-利用Pyinstaller,os库编写一个无限弹窗整蛊文件(上)
前言:本篇文章我们将学习一下如何利用你室友的这个习惯整蛊一下Ta,同时更重要的是借此提醒Ta要注意要做好个人信息的防泄露措施......(声明:本次教学无任何不良引导) 编程思路:本次编程中无限弹窗的实现我们需要调用Py…...
后台管理系统窗体程序:文章管理 > 文章列表
目录 文章列表的的功能介绍: 1、进入页面 2、页面内的各种功能设计 (1)文章表格 (2)删除按钮 (3)编辑按钮 (4)发表文章按钮 (5)所有分类下拉框 &a…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

Springboot 高校报修与互助平台小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,高校报修与互助平台小程序被用户普遍使用,为…...

年度峰会上,抖音依靠人工智能和搜索功能吸引广告主
上周早些时候举行的第五届年度TikTok World产品峰会上,TikTok推出了一系列旨在增强该应用对广告主吸引力的功能。 新产品列表的首位是TikTok Market Scope,这是一个全新的分析平台,为广告主提供整个考虑漏斗的全面视图,使他们能够…...
