在vscode中如何利用git 查看某一个文件的提交记录
在 Visual Studio Code (VSCode) 中,你可以使用内置的 Git 集成来查看某个文件的提交历史。以下是具体步骤:
使用 VSCode 内置 Git 功能
-
打开项目:
- 打开你的项目文件夹,确保该项目已经是一个 Git 仓库(即项目根目录下有一个
.git文件夹)。
- 打开你的项目文件夹,确保该项目已经是一个 Git 仓库(即项目根目录下有一个
-
打开源代码管理视图:
- 你可以通过点击左侧活动栏中的源代码管理图标(看起来像一个分支)来打开源代码管理视图,或者使用快捷键
Ctrl+Shift+G(Windows/Linux)或Cmd+Shift+G(Mac)。
- 你可以通过点击左侧活动栏中的源代码管理图标(看起来像一个分支)来打开源代码管理视图,或者使用快捷键
-
选择文件:
- 在源代码管理视图中,找到并点击你想要查看提交历史的文件。点击文件后,VSCode 会在右侧显示该文件的更改信息。
-
查看提交历史:
- 在文件更改信息的右上角,你会看到一个“…”按钮,点击它。
- 从弹出的菜单中选择“Open File in SCM View”或“Open Changes to Branch”。
- 这将打开一个新的面板,显示该文件的所有提交历史。
使用命令行
如果你更喜欢使用命令行,也可以在 VSCode 的集成终端中执行 Git 命令来查看文件的提交历史:
-
打开集成终端:
- 你可以通过点击顶部菜单栏的
Terminal>New Terminal或者使用快捷键 `Ctrl+``(反引号)来打开集成终端。
- 你可以通过点击顶部菜单栏的
-
运行 Git 命令:
- 在终端中,导航到你的项目根目录。
- 使用以下命令来查看某个文件的提交历史:
git log -- <file_path> - 例如,如果你想查看
src/app.js文件的提交历史,可以运行:git log -- src/app.js

使用 GitLens 扩展
GitLens 是一个非常强大的 VSCode 扩展,可以增强 VSCode 的 Git 功能。安装 GitLens 后,你可以更方便地查看文件的提交历史:
-
安装 GitLens:
- 打开 VSCode 的扩展市场(点击左侧活动栏中的扩展图标,或者使用快捷键
Ctrl+Shift+X)。 - 搜索
GitLens并安装。
- 打开 VSCode 的扩展市场(点击左侧活动栏中的扩展图标,或者使用快捷键
-
查看文件提交历史:
- 打开你想要查看提交历史的文件。
- 在编辑器的右上角,你会看到一个 GitLens 图标(看起来像一个眼睛),点击它。
- 从弹出的菜单中选择“Open File History”。
- 这将打开一个新的面板,显示该文件的所有提交历史,包括每次提交的详细信息。
希望这些方法能帮助你在 VSCode 中轻松查看文件的提交历史!如果有任何其他问题,请随时提问。
相关文章:

在vscode中如何利用git 查看某一个文件的提交记录
在 Visual Studio Code (VSCode) 中,你可以使用内置的 Git 集成来查看某个文件的提交历史。以下是具体步骤: 使用 VSCode 内置 Git 功能 打开项目: 打开你的项目文件夹,确保该项目已经是一个 Git 仓库(即项目根目录下…...

【ShuQiHere】️`adb kill-server` 和 `adb start-server` 命令的作用
📟🔧 【ShuQiHere】️ 🔧📟 在使用 scrcpy 或其他依赖于 ADB(Android Debug Bridge) 的工具时,您可能会遇到需要重启 ADB 服务器的情况。今天,我们将详细解释两个常用的 ADB 命令&a…...

植物明星大乱斗1
能帮到你的话,就给个赞吧 😘 文章目录 scene.hmenuScene.hgameScene.hmainscene.cppmenuScene.cppgameScene.cpp scene.h #pragma once #include <graphics.h>/* 场景菜单角色选择游戏 */ class Scene { public:virtual ~Scene() 0; public:virt…...

信息安全工程师(84)UNIX/Linux操作系统安全分析与防护
前言 UNIX/Linux操作系统,尤其是Linux,以其开放性、稳定性和安全性在服务器、桌面、嵌入式设备和超级计算机中占据重要地位。然而,没有任何操作系统可以百分之百地保证安全,UNIX/Linux也不例外。 一、UNIX/Linux操作系统安全分析 …...

全面解析 Python typing模块与静态类型注解:从基础到高级
在现代软件开发中,代码的可读性、维护性和可靠性至关重要。Python 作为一门动态类型语言,尽管灵活,但也可能带来一些类型上的困扰。Python 的 typing 模块和静态类型注解提供了一种在编写代码时明确类型信息的方法,从而提升代码质…...
Jekins篇(搭建/安装/配置)
目录 一、环境准备 1. Jenkins安装和持续集成环境配置 2. 服务器列表 3. 安装环境 Jekins 环境 4. JDK 环境 5. Maven环境 6. Git环境 方法一:yum安装 二、JenKins 安装 1. JenKins 访问 2. jenkins 初始化配置 三、Jenkins 配置 1. 镜像配置 四、Mave…...

【工具变量】排污权交易政策试点DID(2000-2023)
数据简介:在过去几十年间的“高增长、高能耗、高污染”的经济发展背景下,随着社会各界不断反应高经济增长背后付出的巨大环境代价,中国ZF将节能环保减排纳入长期规划治理中。在2007年,我国开始启动了二氧化硫(SO2&…...

Proteus中数码管动态扫描显示不全(已解决)
文章目录 前言解决方法后记 前言 我是直接把以前写的 51 数码管程序复制过来的,当时看的郭天祥的视频,先送段选,消隐后送位选,最后来个 1ms 的延时。 代码在 Proteus 中数码管静态是可以的,动态显示出了问题——显示…...

证件照尺寸168宽240高,如何手机自拍更换蓝底
在提供学籍照片及一些社会化考试报名时,会要求我们提供尺寸为168*240像素的电子版证件照,本文将介绍如何使用“报名电子照助手”,借助手机拍照功能完成证件照的拍摄和背景更换,特别是如何将照片尺寸调整为168像素宽和240像素高&am…...

力扣.167 两数之和 II two-sum-ii
数组系列 力扣数据结构之数组-00-概览 力扣.53 最大子数组和 maximum-subarray 力扣.128 最长连续序列 longest-consecutive-sequence 力扣.1 两数之和 N 种解法 two-sum 力扣.167 两数之和 II two-sum-ii 力扣.170 两数之和 III two-sum-iii 力扣.653 两数之和 IV two-…...

ipconfig
本文内容来自智谱清言的回答。 ------ 以太网适配器 以太网: 媒体状态 . . . . . . . . . . . . : 媒体已断开连接 连接特定的 DNS 后缀 . . . . . . . : 以太网适配器 以太网: 这部分表示正在显示名为“以太网”的网络适配器的信息。在 Windows 中,默认的以太…...

Qt_day3_信号槽
目录 信号槽 1. 概念 2. 函数原型 3. 连接方式 3.1 自带信号 → 自带槽 3.2 自带信号 → 自定义槽 3.3 自定义信号 4. 信号槽传参 5. 对应关系 5.1 一对多 5.2 多对一 信号槽 1. 概念 之前的程序界面只能看,不能交互,信号槽可以让界面进行人机…...

求从2开始的第n个素数
方法一:暴力法 思路:从2开始,逐个判断每个数是否为素数。素数是除了1和它自身外,不能被其他自然数整除的数。对于每个数m,从2到sqrt(m)遍历,如果能被整除则不是素数。当找到n个素数时停止。 C 代码如下&am…...

【Android】View—基础知识,滑动,弹性滑动
基础知识 什么是View 在 Android 中,View 是用户界面(UI)中的基本组件,用于绘制图形和处理用户交互。所有的 UI 组件(如按钮、文本框、图片等)都是 View 的子类。可以说,View 是构建 Android …...

MYSQL中的两种转义操作
在 MySQL 中,转义字符用于处理特殊字符,以防止语法错误或 SQL 注入攻击,而单双引号都是需要重点注意的字符 可以用转义符\ 和 两个连续的引号 来起到转义引号的作用 转义符转义: 这是users表中的数据 如果查询admin 或者 admin" 用户,可以用转义符\ 两个连…...
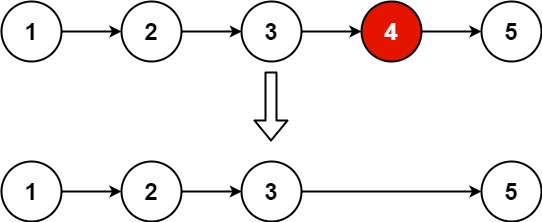
力扣题目解析--删除链表的倒数第n个节点
题目 给你一个链表,删除链表的倒数第 n 个结点,并且返回链表的头结点。 示例 1: 输入:head [1,2,3,4,5], n 2 输出:[1,2,3,5]示例 2: 输入:head [1], n 1 输出:[]示例 3&…...
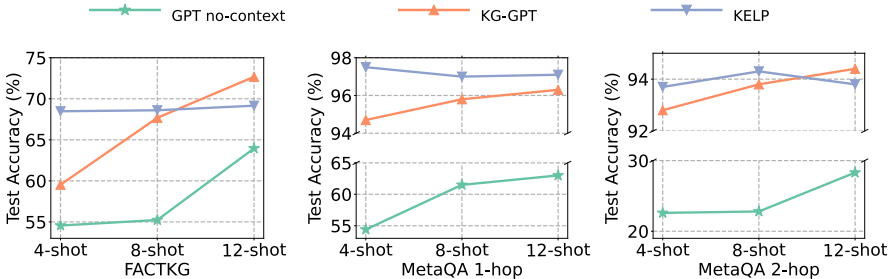
Knowledge Graph-Enhanced Large Language Models via Path Selection
研究背景 研究问题:这篇文章要解决的问题是大型语言模型(LLMs)在生成输出时存在的事实不准确性,即所谓的幻觉问题。尽管LLMs在各种实际应用中表现出色,但当遇到超出训练语料库范围的新知识时,它们通常会生…...

Android 项目模型配置管理
Android 项目配置管理 项目模型相关的配置管理config.gradle文件:build.gradle文件: 参考地址 项目模型相关的配置管理 以下是一个完整的build.gradle和config.gradle示例: config.gradle文件: ext {// 模型相关配置࿰…...

「QT」几何数据类 之 QSizeF 浮点型尺寸类
✨博客主页何曾参静谧的博客📌文章专栏「QT」QT5程序设计📚全部专栏「VS」Visual Studio「C/C」C/C程序设计「UG/NX」BlockUI集合「Win」Windows程序设计「DSA」数据结构与算法「UG/NX」NX二次开发「QT」QT5程序设计「File」数据文件格式「PK」Parasolid…...

Essential Cell Biology--Fifth Edition--Chapter one(2)
1.1.1.3 Living Cells Are Self-Replicating Collections of Catalysts 催化剂集合 生物最常被引用的特性之一是它们的繁殖能力。对于细胞来说,这个过程包括复制它们的遗传物质和其他成分,然后分裂成两个,产生一对子细胞[daughter cells]&a…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...
)
C#学习第29天:表达式树(Expression Trees)
目录 什么是表达式树? 核心概念 1.表达式树的构建 2. 表达式树与Lambda表达式 3.解析和访问表达式树 4.动态条件查询 表达式树的优势 1.动态构建查询 2.LINQ 提供程序支持: 3.性能优化 4.元数据处理 5.代码转换和重写 适用场景 代码复杂性…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

基于PHP的连锁酒店管理系统
有需要请加文章底部Q哦 可远程调试 基于PHP的连锁酒店管理系统 一 介绍 连锁酒店管理系统基于原生PHP开发,数据库mysql,前端bootstrap。系统角色分为用户和管理员。 技术栈 phpmysqlbootstrapphpstudyvscode 二 功能 用户 1 注册/登录/注销 2 个人中…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...

Vue3中的computer和watch
computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...
