【动态规划】斐波那契数列模型总结
一、第 N 个泰波那契数
题目链接: 第 N 个泰波那契数
题目描述:

题目分析:
1、状态表示:
dp[i] 表示:第 i 个斐波那契数的值
2、状态转移方程:
由题意可知第 i 个数等于其前三个数之和
dp[i] = dp[i-1] + dp[i-2] + dp[i-3]
3、初始化:
由于递推公式中存在 i-1、i-2、i-3,当 i=0、1、2的时候,就会出现-1,-2,-3这种非法的下标值,导致数组访问异常。因此,我们需要在填表前将 0,1,2 位置的值初始化。题目中也直接告诉了我们这些位置的初始值:
dp[0]=0 、 dp[1]=1 、 dp[2]=1
4、优化
其实每次在求取 dp[i] 的时候,只需要知道其前三个元素的值即可。也就是说我们在每次更新后只需要保存最后的三个数即可。通过三个数的值就能更新出下一个 dp 值。
代码实现:
class Solution {public int tribonacci(int n) {int[] dp=new int[]{0,1,1};if(n==0)return 0;if(n<3)return 1;for(int i=3;i<=n;i++){dp[i%3]=dp[0]+dp[1]+dp[2];}return dp[n%3];}
}
二、三步问题
题目链接: 三步问题
题目描述:

题目分析:
1、状态表示:
2、状态转移方程:
到达第 i 级台阶的所有方法我们不好确定,但我们可以确定到达第 i 级台阶的上一步只有三种可能:
- 从 i-1置上一级台阶,且到达 i-1 位置的方法数为 dp[i-1]
- 从 i-2置上二级台阶,且到达 i-2 位置的方法数为 dp[i-2]
- 从 i-3置上三级台阶,且到达 i-3 位置的方法数为 dp[i-3]
而到达第 i 级台阶的方法数就应该为其所有上一步的方式之和:
因此dp[i]=dp[i-1] + dp[i-2] + dp[i-3]
注意:由于这里计算的结果可能会很大。因此我们需要对结果进行取模。并且为了防止求和时溢出,在每次求和时都要先取模再求和
3、初始化:
由于递推公式中存在 i-1、i-2、i-3,当 i=0、1、2的时候,就会出现-1,-2,-3这种非法的下标值,导致数组访问异常。因此,我们需要在填表前将 0,1,2 位置的值初始化。由题意很容易就能求出这些位置的初始值:
dp[0]=1 、 dp[1]=2 、 dp[2]=4
代码实现:
class Solution {public int waysToStep(int n) {if(n==1||n==2)return n;if(n==3)return 4;int[] dp=new int[n+1];dp[1]=1;dp[2]=2;dp[3]=4;int MOD=(int)1e9+7;for(int i=4;i<=n;i++){dp[i]=((dp[i-1]+dp[i-2])%MOD+dp[i-3])%MOD;}return dp[n];}
}
三、 使用最小花费爬楼梯
题目链接:使用最小花费爬楼梯
题目描述:

题目分析:
1、状态表示:
2、状态转移方程:
- 先到达 i - 1 的位置,然后⽀付 cost[i - 1] ,接下来⾛⼀步⾛到 i 位置:
dp[i - 1] + csot[i - 1]
- 先到达 i - 2 的位置,然后⽀付 cost[i - 2] ,接下来⾛⼀步⾛到 i 位置:
dp[i - 2] + csot[i - 2]
我们每次只需要取两种情况的最小值即可。
因此:dp[i]=Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])
3、初始化:
很明显 i=0 或 i=1时是无法使用递推公式的。因此我们需要先把他们给初始化了。
由题意可得 dp[0] = dp[1] = 0 ,因为可以直接选择从第0级或第1级台阶开始爬楼梯,不需要任何花费。
代码实现:
class Solution {public int minCostClimbingStairs(int[] cost) {int n=cost.length;int[] dp=new int[n+1];for(int i=2;i<=n;i++){dp[i]=Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}return dp[n];}
}
四、解码方法
题目链接: 解码方法
题目描述:

题目分析:
1、状态表示:
2、状态转移方程:
- 让 i 位置上的数单独解码成⼀个字⺟;
- 让 i 位置上的数与 i - 1 位置上的数结合,解码成⼀个字⺟。
- 解码成功:当 i 位置上的数在 [1, 9] 之间的时候,说明 i 位置上的数是可以单独解码的,那么此时 [0, i] 区间上的解码⽅法应该等于 [0, i - 1] 区间上的解码⽅法。因为 [0, i - 1] 区间上的所有解码结果,后⾯填上⼀个 i 位置解码后的字⺟就可以了。此时 dp[i] = dp[i - 1] ;
- 解码失败:当 i 位置上的数是 0 的时候,说明 i 位置上的数是不能单独解码的,那么此时 [0, i] 区间上不存在解码⽅法。因为 i 位置如果单独参与解码,但是解码失败了,那么前⾯做的努⼒就全部⽩费了。此时 dp[i] = 0 。
- 解码成功:当结合的数在 [10, 26] 之间的时候,说明 [i - 1, i] 两个位置是可以解码成功的,那么此时 [0, i] 区间上的解码⽅法应该等于 [0, i - 2 ] 区间上的解码⽅法,原因同上。此时 dp[i] = dp[i - 2]
- 解码失败:当结合的数在 [0, 9] 和 [27 , 99] 之间的时候,说明两个位置结合后解码失败(这⾥⼀定要注意 00 01 02 03 04 ...... 这⼏种情况),那么此时 [0, i] 区间上的解码⽅法就不存在了,原因依旧同上。此时 dp[i] = 0 。
- 当 s[i] 上的数在 [1, 9] 区间上时: dp[i] += dp[i - 1]
- 当 s[i - 1] 与 s[i] 上的数结合后,在 [10, 26] 之间的时候: dp[i] += dp[i - 2]
- 如果上述两个判断都不成⽴,说明没有解码⽅法, dp[i] 就是默认值 0 。
3、初始化:
代码实现:
class Solution {public int numDecodings(String s) {char[] cs=s.toCharArray();int n=s.length();if(cs[0]-'0'==0)return 0;int[] dp=new int[n+1];dp[1]=1;dp[0]=1;for(int i=2;i<=n;i++){if(cs[i-1]-'0'!=0)dp[i]=dp[i-1];if(cs[i-2]-'0'==0)continue;int x=(cs[i-2]-'0')*10+cs[i-1]-'0';if(x<=26){dp[i]+=dp[i-2];}}return dp[n];}
}
那么本篇文章就到此为止了,如果觉得这篇文章对你有帮助的话,可以点一下关注和点赞来支持作者哦。如果有什么讲的不对的地方欢迎在评论区指出,希望能够和你们一起进步✊

相关文章:

【动态规划】斐波那契数列模型总结
一、第 N 个泰波那契数 题目链接: 第 N 个泰波那契数 题目描述: 题目分析: 1、状态表示: dp[i] 表示:第 i 个斐波那契数的值 2、状态转移方程: 由题意可知第 i 个数等于其前三个数之和 dp[i] dp[i-…...

EasyUI弹出框行编辑,通过下拉框实现内容联动
EasyUI弹出框行编辑,通过下拉框实现内容联动 需求 实现用户支付方式配置,当弹出框加载出来的时候,显示用户现有的支付方式,datagrid的第一列为conbobox,下来选择之后实现后面的数据直接填充; 点击新增:新…...
使用 PageOffice 实现word文件在线留痕)
国产linux系统(银河麒麟,统信uos)使用 PageOffice 实现word文件在线留痕
PageOffice 国产版 :支持信创系统,支持银河麒麟V10和统信UOS,支持X86(intel、兆芯、海光等)、ARM(飞腾、鲲鹏、麒麟等)、龙芯(LoogArch)芯片架构。 查看本示例演示效果 …...
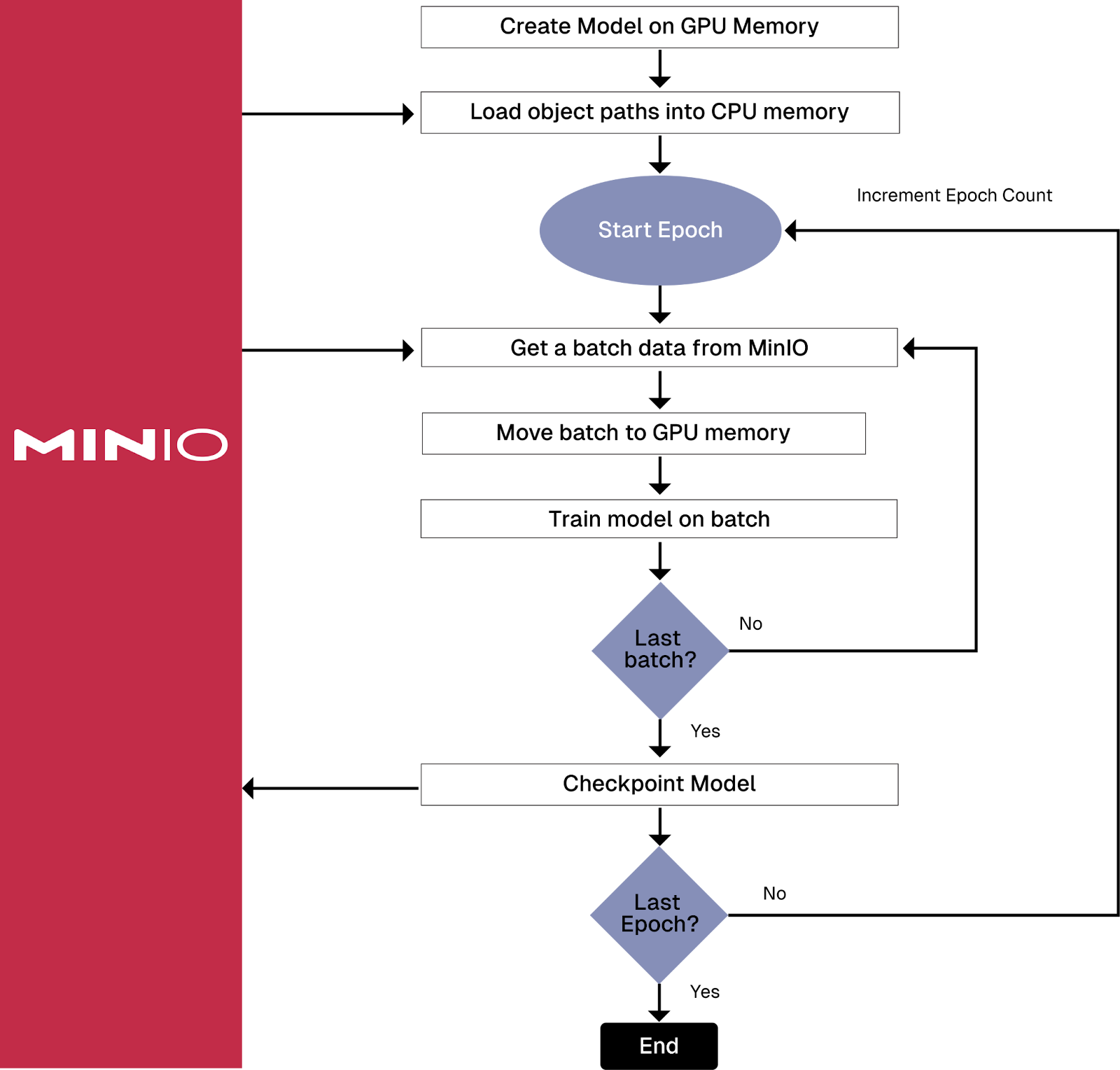
使用亚马逊 S3 连接器为 PyTorch 和 MinIO 创建地图式数据集
在深入研究 Amazon 的 PyTorch S3 连接器之前,有必要介绍一下它要解决的问题。许多 AI 模型需要使用无法放入内存的数据进行训练。此外,许多为计算机视觉和生成式 AI 构建的真正有趣的模型使用的数据甚至无法容纳在单个服务器附带的磁盘驱动器上。解决存…...

自动化运维:提升效率与稳定性的关键技术实践
自动化运维:提升效率与稳定性的关键技术实践 在数字化转型的浪潮中,企业对于IT系统的依赖日益加深,系统的复杂性和规模也随之膨胀。面对这一挑战,传统的运维模式——依靠人工进行服务器的监控、配置变更、故障排查等任务…...

Google Go编程风格指南-介绍
关于 首先应该明确的是:Go语言是Google搞出来的,这个编程风格指南也是它提出来的,详见:https://google.github.io/styleguide/go/。 然后国内翻译组跟上,于是有了中文版:https://gocn.github.io/stylegui…...

思科模拟器路由器配置实验
一、实验目的 了解路由器的作用。掌握路由器的基本配置方法。掌握路由器模块的使用和互连方式。 二、实验环境 设备: 2811 路由器 1 台计算机 2 台Console 配置线 1 根网线若干根 拓扑图:实验拓扑图如图 8-1 所示。计算机 IP 地址规划:如表…...

机器学习—选择激活函数
可以为神经网络中的不同神经元选择激活函数,我们将从如何为输出层选择它的一些指导开始,事实证明,取决于目标标签或地面真相标签y是什么,对于输出层的激活函数,将有一个相当自然的选择,然后看看激活函数的选…...

[ Linux 命令基础 4 ] Linux 命令详解-文本处理命令
🍬 博主介绍 👨🎓 博主介绍:大家好,我是 _PowerShell ,很高兴认识大家~ ✨主攻领域:【渗透领域】【数据通信】 【通讯安全】 【web安全】【面试分析】 🎉点赞➕评论➕收藏 养成习…...

Odoo:免费开源的钢铁冶金行业ERP管理系统
文 / 开源智造 Odoo亚太金牌服务 简介 Odoo免费开源ERP集成计质量设备大宗原料采购,备件设材全生命周期,多业务模式货控销售,全要素追溯单品,无人值守计量物流,大宗贸易交易和精细化成本管理等方案;覆盖…...

33.Redis多线程
1.Redis队列与Stream Redis5.0 最大的新特性就是多出了一个数据结构 Stream,它是一个新的强大的支持多播的可持久化的消息队列。 Redis Stream 的结构如上图所示,每一个Stream都有一个消息链表,将所有加入的消息都串起来,每个消息都有一个唯…...

【Python】解析 XML
1、Python 对 XML 的解析 1.1 SAX (simple API for XML ) SAX 解析器使用事件驱动模型,通过在解析XML的过程中触发一个个的事件并调用用户定义的回调函数来处理XML文件。 xml.sax 模块牺牲了便捷性来换取速度和内存占用。 事件驱动指一种基于回调(ca…...

【复平面】-复数相乘的几何性质
文章目录 从数学上证明1. 计算乘积 z 1 ⋅ z 2 z_1 \cdot z_2 z1⋅z22. 应用三角恒等式3. 得出结果 从几何角度证明1.给出待乘的复数 u i u_i ui2.给出任意复数 l l l3.复数 l l l 在不同坐标轴下的表示图 首先说结论: 在复平面中,两个复数&a…...

为什么ta【给脸不要脸】:利他是一种选择,善良者的自我救赎与智慧策略
你满腔热忱,他却视而不见; 你伸出援手,他却恩将仇报; 你谦让包容,他却得寸进尺; 你善意提拔,他却并不领情,反而“给脸不要脸”。 所有人都曾被这种“好心当成驴肝肺”遭遇内耗&a…...

mysql 配置文件 my.cnf 增加 lower_case_table_names = 1 服务启动不了的原因
原因:在MySQL8.0之后的版本,只允许在数据库初始化时指定,之后不允许修改了 mysql 配置文件 my.cnf 增加 lower_case_table_names 1 服务启动不了 报错信息:Job for mysqld.service failed because the control process exited …...
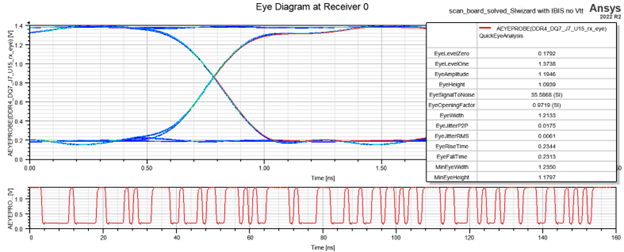
SIwave:释放 SIwizard 求解器的强大功能
SIwave 是一种电源完整性和信号完整性工具。SIwizard 是 SIwave 中 SI 分析的主要工具,也是本博客的主题。 SIwizard 用于研究 RF、clock 和 control traces 的信号完整性。该工具允许用户进行瞬态分析、眼图分析和 BER 计算。用户可以将 IBIS 和 IBIS-AMI 模型添加…...
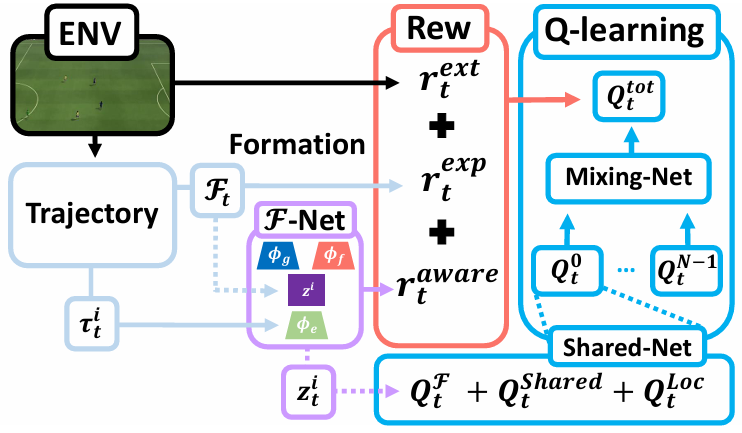
强化学习不愧“顶会收割机”!2大创新思路带你上大分,毕业不用愁!
强化学习之父Richard Sutton悄悄搞了个大的,提出了一个简单思路:奖励聚中。这思路简单效果却不简单,等于是给几乎所有的强化学习算法上了一个增强buff,所以这篇论文已经入选了首届强化学习会议(RLC 2024)&a…...

mac 修改启动图图标数量
调整每行显示图标数量: defaults write com.apple.dock springboard-rows -int 7 调整每列显示的数量 defaults write com.apple.dock springboard-columns -int 8 最后重置一下启动台 defaults write com.apple.dock ResetLaunchPad -bool TRUE;killall Dock 其…...

网站架构知识之Ansible进阶(day022)
1.handler触发器 应用场景:一般用于分发配置文件时候,如果配置文件有变化,则重启服务,如果没有变化,则不重启服务 案列01:分发nfs配置文件,若文件发生改变则重启服务 2.when判断 用于给ans运…...

VMware调整窗口为可以缩小但不改变显示内容的大小
也就是缩小窗口不会影响内容的大小 这样设置就好...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

七、数据库的完整性
七、数据库的完整性 主要内容 7.1 数据库的完整性概述 7.2 实体完整性 7.3 参照完整性 7.4 用户定义的完整性 7.5 触发器 7.6 SQL Server中数据库完整性的实现 7.7 小结 7.1 数据库的完整性概述 数据库完整性的含义 正确性 指数据的合法性 有效性 指数据是否属于所定…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...
