【复平面】-复数相乘的几何性质
文章目录
- 从数学上证明
- 1. 计算乘积 z 1 ⋅ z 2 z_1 \cdot z_2 z1⋅z2
- 2. 应用三角恒等式
- 3. 得出结果
- 从几何角度证明
首先说结论:
在复平面中,两个复数(即向量)相乘时,满足模长相乘,角度相加的性质。
从数学上证明
假设两个复数 ( z 1 z_1 z1 ) 和 ( z 2 z_2 z2 ) 表示为:
z 1 = r 1 ( cos θ 1 + i sin θ 1 ) z_1 = r_1 (\cos \theta_1 + i \sin \theta_1) z1=r1(cosθ1+isinθ1)
z 2 = r 2 ( cos θ 2 + i sin θ 2 ) z_2 = r_2 (\cos \theta_2 + i \sin \theta_2) z2=r2(cosθ2+isinθ2)
其中:
- ( r 1 = ∣ z 1 ∣ r_1 = |z_1| r1=∣z1∣ ) 和 ( r 2 = ∣ z 2 ∣ r_2 = |z_2| r2=∣z2∣ ) 分别是 ( z 1 z_1 z1 ) 和 ( z 2 z_2 z2 ) 的模长,
- ( θ 1 \theta_1 θ1 ) 和 ( θ 2 \theta_2 θ2 ) 分别是 ( z 1 z_1 z1 ) 和 ( z 2 z_2 z2 ) 的辐角(即相对于实轴的角度)。
1. 计算乘积 z 1 ⋅ z 2 z_1 \cdot z_2 z1⋅z2
我们将 ( z 1 z_1 z1 ) 和 ( z 2 z_2 z2 ) 相乘,得到:
z 1 ⋅ z 2 = r 1 ( cos θ 1 + i sin θ 1 ) ⋅ r 2 ( cos θ 2 + i sin θ 2 ) z_1 \cdot z_2 = r_1 (\cos \theta_1 + i \sin \theta_1) \cdot r_2 (\cos \theta_2 + i \sin \theta_2) z1⋅z2=r1(cosθ1+isinθ1)⋅r2(cosθ2+isinθ2)
使用分配律展开:
z 1 ⋅ z 2 = r 1 r 2 [ ( cos θ 1 cos θ 2 − sin θ 1 sin θ 2 ) + i ( cos θ 1 sin θ 2 + sin θ 1 cos θ 2 ) ] z_1 \cdot z_2 = r_1 r_2 \left[ (\cos \theta_1 \cos \theta_2 - \sin \theta_1 \sin \theta_2) + i (\cos \theta_1 \sin \theta_2 + \sin \theta_1 \cos \theta_2) \right] z1⋅z2=r1r2[(cosθ1cosθ2−sinθ1sinθ2)+i(cosθ1sinθ2+sinθ1cosθ2)]
2. 应用三角恒等式
根据加法公式的三角恒等式,有:
cos ( θ 1 + θ 2 ) = cos θ 1 cos θ 2 − sin θ 1 sin θ 2 \cos(\theta_1 + \theta_2) = \cos \theta_1 \cos \theta_2 - \sin \theta_1 \sin \theta_2 cos(θ1+θ2)=cosθ1cosθ2−sinθ1sinθ2
sin ( θ 1 + θ 2 ) = cos θ 1 sin θ 2 + sin θ 1 cos θ 2 \sin(\theta_1 + \theta_2) = \cos \theta_1 \sin \theta_2 + \sin \theta_1 \cos \theta_2 sin(θ1+θ2)=cosθ1sinθ2+sinθ1cosθ2
将这些恒等式代入到上面的表达式中,我们得到:
z 1 ⋅ z 2 = r 1 r 2 ( cos ( θ 1 + θ 2 ) + i sin ( θ 1 + θ 2 ) ) z_1 \cdot z_2 = r_1 r_2 \left( \cos(\theta_1 + \theta_2) + i \sin(\theta_1 + \theta_2) \right) z1⋅z2=r1r2(cos(θ1+θ2)+isin(θ1+θ2))
3. 得出结果
根据复数的极坐标形式,这个结果可以写成:
z 1 ⋅ z 2 = r 1 r 2 ⋅ e i ( θ 1 + θ 2 ) z_1 \cdot z_2 = r_1 r_2 \cdot e^{i (\theta_1 + \theta_2)} z1⋅z2=r1r2⋅ei(θ1+θ2)
因此,我们得出结论:两个复数相乘时,其模长是各自模长的乘积,辐角是各自辐角的和,即满足“模长相乘,角度相加”的性质。
从几何角度证明
本质上就是坐标轴的变换
1.给出待乘的复数 u i u_i ui
{ u = a + b i u i = − b + a i \left\{\begin{array}{l} u=a+b i \\ u i=-b+a i \end{array}\right. {u=a+biui=−b+ai
( a , b ) ⋅ ( − b , a ) = 0 (a,b)\cdot(-b,a)=0 (a,b)⋅(−b,a)=0由于内积为0,故u与ui正交
2.给出任意复数 l l l
所以 ∀ l = x + y i \forall l=x+y_{i} ∀l=x+yi与u相乘可以在新的坐标轴u、ui下表示,其与坐标轴角度与在原先坐标轴下相同。
所以两个复数(即向量)相乘时,满足角度相加的性质。
{ ∀ l = x + y i l ⋅ u = ( x + y i ) ⋅ u = x u + y u i \left\{\begin{array}{l} \forall l=x+y_{i} \\ l \cdot u=\left(x+y_{i}\right) \cdot u=x u+y u i \end{array}\right. {∀l=x+yil⋅u=(x+yi)⋅u=xu+yui
3.复数 l l l 在不同坐标轴下的表示图
 |  |
相关文章:

【复平面】-复数相乘的几何性质
文章目录 从数学上证明1. 计算乘积 z 1 ⋅ z 2 z_1 \cdot z_2 z1⋅z22. 应用三角恒等式3. 得出结果 从几何角度证明1.给出待乘的复数 u i u_i ui2.给出任意复数 l l l3.复数 l l l 在不同坐标轴下的表示图 首先说结论: 在复平面中,两个复数&a…...

为什么ta【给脸不要脸】:利他是一种选择,善良者的自我救赎与智慧策略
你满腔热忱,他却视而不见; 你伸出援手,他却恩将仇报; 你谦让包容,他却得寸进尺; 你善意提拔,他却并不领情,反而“给脸不要脸”。 所有人都曾被这种“好心当成驴肝肺”遭遇内耗&a…...

mysql 配置文件 my.cnf 增加 lower_case_table_names = 1 服务启动不了的原因
原因:在MySQL8.0之后的版本,只允许在数据库初始化时指定,之后不允许修改了 mysql 配置文件 my.cnf 增加 lower_case_table_names 1 服务启动不了 报错信息:Job for mysqld.service failed because the control process exited …...
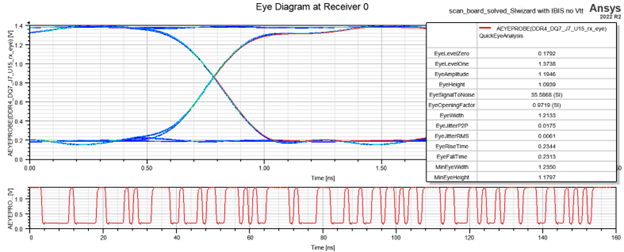
SIwave:释放 SIwizard 求解器的强大功能
SIwave 是一种电源完整性和信号完整性工具。SIwizard 是 SIwave 中 SI 分析的主要工具,也是本博客的主题。 SIwizard 用于研究 RF、clock 和 control traces 的信号完整性。该工具允许用户进行瞬态分析、眼图分析和 BER 计算。用户可以将 IBIS 和 IBIS-AMI 模型添加…...
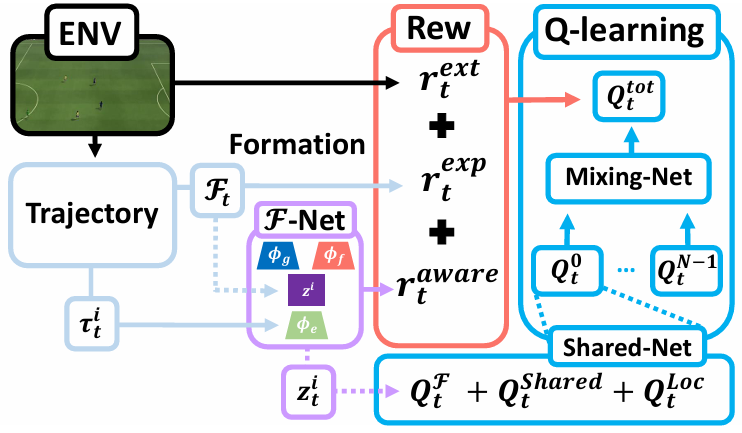
强化学习不愧“顶会收割机”!2大创新思路带你上大分,毕业不用愁!
强化学习之父Richard Sutton悄悄搞了个大的,提出了一个简单思路:奖励聚中。这思路简单效果却不简单,等于是给几乎所有的强化学习算法上了一个增强buff,所以这篇论文已经入选了首届强化学习会议(RLC 2024)&a…...

mac 修改启动图图标数量
调整每行显示图标数量: defaults write com.apple.dock springboard-rows -int 7 调整每列显示的数量 defaults write com.apple.dock springboard-columns -int 8 最后重置一下启动台 defaults write com.apple.dock ResetLaunchPad -bool TRUE;killall Dock 其…...

网站架构知识之Ansible进阶(day022)
1.handler触发器 应用场景:一般用于分发配置文件时候,如果配置文件有变化,则重启服务,如果没有变化,则不重启服务 案列01:分发nfs配置文件,若文件发生改变则重启服务 2.when判断 用于给ans运…...

VMware调整窗口为可以缩小但不改变显示内容的大小
也就是缩小窗口不会影响内容的大小 这样设置就好...

Vue 3 中,ref 和 reactive的区别
在 Vue 3 中,ref 和 reactive 是两种用于创建响应式数据的方法。它们有一些关键的区别和适用场景。以下是它们的主要区别: ref 用途: ref 主要用于处理基本数据类型(如字符串、数字、布尔值等)以及需要单独响应的复杂…...

window 利用Putty免密登录远程服务器
1 在本地电脑用putty-gen生成密钥 参考1 参考2 2 服务器端操作 将公钥上传至Linux服务器。 复制上述公钥到服务器端的authorized_keys文件 mkdir ~/.ssh vi ~/.ssh/authorized_keys在vi编辑器中,按下ShiftInsert键或者右键选择粘贴,即可将剪贴板中的文…...

OGNL表达式
介绍 OGNL生来就是为了简化Java属性的取值,比如想根据名称name引用当前上下文环境中的对象,则直接键入即可,如果想要引用当前上下文环境中对象text的属性title,则键入text.title即可。如果想引用对象的非值属性,OGNL也…...

AI 大模型重塑软件开发流程的现状与未来展望
 大家好,我是程序员小羊! 前言: 随着AI技术,尤其是大模型的快速发展,软件开发领域正在经历深刻…...

Spring Boot 的核心注解
一、引言 Spring Boot 作为一种流行的 Java 开发框架,以其简洁高效的开发方式受到广泛关注。其中,核心注解在 Spring Boot 应用的开发中起着至关重要的作用。理解这些注解的含义和用法,对于充分发挥 Spring Boot 的优势至关重要。本文将深入剖…...

蓝桥杯备考——算法
一、排序 冒泡排序、选择排序、插入排序、 快速排序、归并排序、桶排序 二、枚举 三、二分查找与二分答案 四、搜索(DFS) DFS(DFS基础、回溯、剪枝、记忆化) 1.DFS算法(深度优先搜索算法) 深度优先搜…...

MutationObserver与IntersectionObserver的区别
今天主要是分享一下MutationObserver和IntersectionObserver的区别,希望对大家有帮助! MutationObserver 和 IntersectionObserver 的区别 MutationObserver 作用:用于监听 DOM 树的变动,包括:元素的属性、子元素列表或节点文本的…...
生产与配置
1.鲁滨孙克苏鲁经济 鲁滨孙克苏鲁经济是一种非常简单的自给自足的经济,劳动时间与休息时间总和为总的时间。 即 摘椰子的数量为劳动时间的函数 由于鲁滨孙喜欢椰子,厌恶劳动时间,因此无差异曲线表现为厌恶品的形态。 根据无差异曲线和生…...

Android Kotlin Flow 冷流 热流
在 Android 开发中,Flow 是 Kotlin 协程库的一部分,用于处理异步数据流的一个组件。本质上,Flow 是一个能够异步生产多个值的数据流,与 suspend 函数返回单个值的模式相对应。Flow 更类似于 RxJava 中的 Observable,但…...

订单日记助力“实峰科技”提升业务效率
感谢北京实峰科技有限公司选择使用订单日记! 北京实峰科技有限公司,成立于2022年,位于北京市石景区,是一家以从事生产、销售微特电机、输配电及控制设备等业务为主的企业。 在业务不断壮大的过程中,想使用一种既能提…...

如何安装和配置JDK17
教程目录 零、引言1、新特性概览2、性能优化3、安全性增强4、其他改进5、总结 一、下载安装二、环境配置三、测试验证 零、引言 JDK 17(Java Development Kit 17)是Java平台的一个重要版本,它带来了许多新特性和改进,进一步提升了…...

智能化温室大棚控制系统设计(论文+源码)
1 系统的功能及方案设计 本次智能化温室大棚控制系统的设计其系统整体结构如图2.1所示,整个系统在器件上包括了主控制器STC89C52,温湿度传感器DHT11,LCD1602液晶,继电器,CO2传感器,光敏电阻,按…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...
