webpack的常见配置
Webpack 是一个现代 JavaScript 应用的模块打包工具,用于将项目中的多个文件和依赖打包成浏览器可以识别的文件,通常是一个或多个 JavaScript、CSS 或其他静态资源的 bundle(将多个模块或文件合并成一个或几个文件的过程,这些合并后的文件被称为 “bundles”)。
主要功能与优点:
- 模块化:支持 ES6 的模块系统,以及 CommonJS、AMD 等模块标准。
- 加载静态资源:支持加载和打包 CSS、图片、字体等静态资源。
- 代码拆分(Code Splitting):按需加载,提高首屏加载速度。
- 插件系统:可通过各种插件扩展功能,如压缩代码、自动生成 HTML 等。
- 热模块替换(HMR):开发环境下自动更新页面,无需刷新。
常见配置:
-
入口文件(entry):指定项目的入口文件。
module.exports = {entry: './src/index.js', }; -
输出文件(output):配置打包后的文件名和输出路径。
module.exports = {output: {filename: 'bundle.js',path: path.resolve(__dirname, 'dist'),}, }; -
加载器(Loaders):处理非 JavaScript 文件如 CSS、图片等。
module: {rules: [{test: /\.css$/,use: ['style-loader', 'css-loader'],},], }, -
插件(Plugins):用于执行各种任务,如生成 HTML 文件或压缩代码。
const HtmlWebpackPlugin = require('html-webpack-plugin'); module.exports = {plugins: [new HtmlWebpackPlugin({template: './src/index.html',}),], };
使用场景:
- 单页面应用(SPA)开发:Webpack 将多个模块和资源打包成一个高效的文件,提升性能。
- 前端资源优化:如代码压缩、图片优化、按需加载。
- 项目自动化:通过插件系统实现各种构建任务的自动化。
相关文章:

webpack的常见配置
Webpack 是一个现代 JavaScript 应用的模块打包工具,用于将项目中的多个文件和依赖打包成浏览器可以识别的文件,通常是一个或多个 JavaScript、CSS 或其他静态资源的 bundle(将多个模块或文件合并成一个或几个文件的过程,这些合并…...

text-embedding-ada-002;BGE模型;M3E模型是Moka Massive Mixed Embedding;BERT
目录 text-embedding-ada-002 一、模型概述 二、模型功能 三、模型特点 四、模型应用 五、模型优势 BGE模型 一、模型背景与特点 二、模型性能与表现 三、模型迭代与发展 M3E模型是Moka Massive Mixed Embedding 一、基本信息 二、技术特点 三、应用场景 四、性能…...
WebRTC 环境搭建
主题 本文主要描述webrtc开发过程中所需的环境搭建 环境: 运行环境:ubuntu 20.04 Node.js环境搭建 安装编译 Node.js 所需的依赖包: sudo apt-get update sudo apt-get install -y build-essential libssl-dev 下载 Node.js 源码: curl -sL htt…...

FastHTML快速入门:http方法,CSS文件和内联样式,其他静态媒体文件位置
HTTP方法 FastHTML通过函数名与HTTP方法进行匹配。到目前为止,我们定义的URL路由都是针对HTTP GET方法的,这是网页最常见的方法。 表单提交通常作为HTTP POST发送。在处理更动态的网页设计时,也就是所谓的单页应用(SPA࿰…...
项目管理和研发管理中的痛点及其解决方案
在现代企业中,研发管理和项目管理面临着多重挑战,包括资源配置不当、沟通不畅、目标不明确、进度控制困难等。这些痛点不仅影响项目的顺利推进,还可能导致企业在市场竞争中处于劣势。尤其是在资源配置不当方面,企业往往难以合理分…...

机器学习(基础1)
数据集 sklearn玩具数据集 数据量小,数据在sklearn库的本地,只要安装了sklearn,不用上网就可以获取 sklearn现实世界数据集 数据量大,数据只能通过网络获取(为国外数据集,下载需要梯子) skle…...

我谈维纳(Wiener)复原滤波器
Rafael Gonzalez的《数字图像处理》中,图像复原这章内容几乎全错。上篇谈了图像去噪,这篇谈图像复原。 图像复原也称为盲解卷积,不处理点扩散函数(光学传递函数)的都不是图像复原。几何校正不属于图像复原,…...

怎么看真假国企啊?怎么识别假冒国企的千层套路?
一、怎么看真假国企啊? 1.使用具有迷惑性的名称:假冒国企往往在名称中使用“中国”、“中”、“国”等字样,或与知名国企名称相似的字号,以增加其可信度。 2.注册资本虚高:为了显示实力,假冒国企可能会在…...

C#中break和continue的区别?
在C#编程语言中,break和continue是两个用于控制循环流程的关键字,但它们的作用和用途有所不同。 break关键字 break关键字用于立即终止它所在的最内层循环或switch语句,并跳出该循环或switch块。程序执行将继续进行循环或switch语句之后的下一…...

Linux部署nginx访问文件403
问题描述:在linux服务器上通过nginx部署,访问文件403 新配置了一个用户来部署服务,将部署文件更新到原有目录下,结果nginx访问403 原因:没有配置文件的读写权限,默认不可读写,nginx无法访问到文…...

华为OD机试 - 数字排列 - 深度优先搜索dfs算法(Python/JS/C/C++ 2024 C卷 200分)
华为OD机试 2024E卷题库疯狂收录中,刷题点这里 专栏导读 本专栏收录于《华为OD机试真题(Python/JS/C/C)》。 刷的越多,抽中的概率越大,私信哪吒,备注华为OD,加入华为OD刷题交流群,…...

Scrapy爬取heima论坛所有页面内容并保存到数据库中
前期准备: Scrapy入门_win10安装scrapy-CSDN博客 新建 Scrapy项目 scrapy startproject mySpider03 # 项目名为mySpider03 进入到spiders目录 cd mySpider03/mySpider03/spiders 创建爬虫 scrapy genspider heima bbs.itheima.com # 爬虫名为heima &#…...

Kafka参数了解
Kafka配置参数完整说明 1. 基础配置 参数名说明推荐值参考值broker.idbroker的唯一标识符每个节点唯一的整数1delete.topic.enable是否允许删除topictruetruelistenersbroker监听地址SASL_PLAINTEXT://host:9092SASL_PLAINTEXT://172.24.77.15:9092advertised.listeners对外发…...

sql专题 之 where和join on
文章目录 前言where介绍使用过滤结果集关联两个表 连接外连接内连接自然连接 使用inner join和直接使用where关联两个表的区别总结 前言 从数据库查询数据时,一张表不足以查询到我们想要的数据,更多的时候我们需要联表查询。 联表查询我们一般会使用连接…...

day12:版本控制器
版本控制 使用到的命令: ls -al查看当前目录下的文件及文件夹mkdir新建目录rm -rf递归强制删除文件夹 一、安装配置 1、下载地址 Git 2、初始配置 #用户名 git config --global user.name "自定义用户名" #邮箱(公司的联系方式--追责&…...

第四十一章 Vue之初识VueX
目录 一、引言 1.1. vuex的概念 1.2. vuex使用场景 1.3. 优势 二、创建演示项目 2.1. 构建项目步骤 2.2. 项目最终生成结构 2.3. 创建项目文件 2.3.1. App.vue 2.3.2. Son1.vue 2.3.3. Son2.vue 三、创建一个空仓库 3.1. 安装vuex 3.2. 新建仓库 3.3. 挂载仓库…...
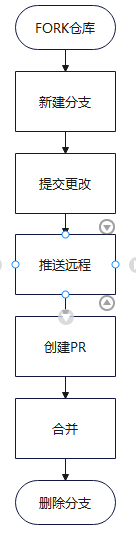
GIT的基本使用与进阶
GIT的简单入门 一.什么是git? Git 是一个开源的分布式版本控制系统,用于跟踪文件更改、管理代码版本以及协作开发。它主要由 Linus Torvalds 于 2005 年创建,最初是为 Linux 内核开发而设计的。如今,Git 已经成为现代软件开发中…...

【Linux系统】—— 基本指令(二)
【Linux系统】—— 基本指令(二) 1 「alias」命令1.1 「ll」命令1.2 「alias」命令 2 「rmdir」指令与「rm」指令2.1 「rmdir」2.2 「rm」2.2.1 「rm」 删除普通文件2.2.2 「rm」 删除目录2.2.3 『 * 』 通配符 3 「man」 指令4 「cp」 指令4.1 拷贝普通…...

MFC工控项目实例三十实现一个简单的流程
启动按钮夹紧 密闭,时间0到平衡 进气,时间1到进气关,时间2到平衡关 检测,时间3到平衡 排气,时间4到夹紧开、密闭开、排气关。 相关代码 void CSEAL_PRESSUREDlg::OnTimer_2(UINT nIDEvent_2) {// if (nIDEvent_21 &am…...

【Android、IOS、Flutter、鸿蒙、ReactNative 】文本点击事件
Android Studio 版本 Android Java TextView 实现 点击事件 参考 import androidx.appcompat.app.AppCompatActivity; import android.os.Bundle; import android.util.Log; import android.view.View; import android.widget.TextView; import android.widget.Toast;public c…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...
