【计算机基础——数据结构——AVL平衡二叉树】
1. BST二叉查找树
1.1 BST二叉查找树的特性
- 左子树上所有结点的值均小于或等于它的根结点的值。
- 右子树上所有结点的值均大于或等于它的根结点的值。
- 左、右子树也分别为二叉排序树。
1.2 BST二叉查找树的缺点
- 二叉查找树是有缺点的,在不断插入的时候,有可能出现这样一种情况:很容易“退化”成链表,
- 如果bst 树的节点正好从大到小的插入,此时树的结构也类似于链表结构,这时候的查询或写入耗时与链表相同。

为了避免这种特殊的情况发生,引入了平衡二叉树(AVL)和红黑树(red-black tree)
2. AVL平衡二叉树
平衡二叉树也叫AVL(发明者名字简写),也属于二叉搜索树的一种,与其不同的是AVL通过机制保证其自身的平衡。
AVL树是最先发明的自平衡二叉查找树。
在AVL树中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树。
增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。
2.1 AVL树的特性
AVL树本质上还是一棵二叉搜索树,它有以下特性:
- 特性1: 对于任何一颗子树的root根结点而言,它的左子树任何节点的key一定比root小,而右子树任何节点的key 一定比root大;
- 特性2:对于AVL树而言,其中任何子树仍然是AVL树;
- 特性3:每个节点的左右子节点的高度之差的绝对值最多为1;
在插入、删除树节点的时候,如果破坏了以上的原则,AVL树会自动进行调整使得以上三条原则仍然成立。
2.2 AVL树的平衡功能
举个例子,下左图为AVL树最长的2节点与最短的8节点高度差为1;
当插入一个新的节点后,根据上面第一条原则,它会出现在2节点的左子树,但这样一来就违反了原则3。

此时AVL树会通过节点的旋转进行进行平衡,
AVL调整的过程称之为左旋和右旋,左旋就是逆时针转,右旋是顺时针转
2.3 AVL平衡的调整过程
调整的过程:
- 确定旋转支点(pivot):这个旋转支点就是失去平衡这部分树,在自平衡之后的根节点,平衡的调整过程,需要根据pivot它来进行旋转。我们只关注失衡子树的根结点 及它的子节点和孙子节点即可。
- 判断AVL失衡的类型:包含左左结构失衡(LL型失衡)、右右结构失衡(RR型失衡)、左右结构失衡(LR型失衡)、右左结构失衡(RL型失衡)
- 根据失衡的类型进行相应的旋转
2.3.1 场景1:LL失衡-左左结构失衡(右旋)
在结点Root的 左结点(L) 的 左子树(L) 上做了插入元素的操作,我们称这种情况为 左左型 ,我们应该进行右旋转。

2.3.2 场景2:RR型失衡:右右结构失衡(左旋)
在结点Root的 右结点(R) 的 右子树(R) 上做了插入元素的操作,我们称这种情况为右右型 ,我们应该进行左旋转。

2.3.3 场景3: LR型失衡:左右失衡(左旋+右旋):
在结点Root的 左结点(L) 的 右子树(R) 上做了插入元素的操作,我们称这种情况为左右型 ,我们应该进行左旋转+右旋转。

2.3.4 场景4:RL失衡: 右左结构 (右旋+左旋):
在结点Root的 右结点(R) 的 左子树(L) 上做了插入元素的操作,我们称这种情况为右左型 ,我们应该进行右旋转+左旋转。

3. 代码实现+详细注解
3.1 基本结构+操作
package mainimport "fmt"// AVL树的节点
type Node struct {Key intHeight intLeft *NodeRight *Node
}type AVLTree struct {Root *Node
}// 返回节点的高度
func height(n *Node) int {if n == nil {return 0}return n.Height
}func max(a, b int) int {if a > b {return a}return b
}// 返回当前节点的平衡因子
func getBalance(n *Node) int {if n == nil {return 0}return height(n.Left) - height(n.Right)
}// 右旋
func rightRotate(root *Node) *Node {//pivot是新的根节点,T2是要转移的子树的根pivot := root.LeftT2 := pivot.Rightpivot.Right = rootroot.Left = T2// 重新计算两个调整后的节点高度root.Height = max(height(root.Left), height(root.Right)) + 1pivot.Height = max(height(pivot.Left), height(pivot.Right)) + 1return pivot
}// 右旋
func leftRotate(root *Node) *Node {//pivot是新的根节点,T2是要转移的子树的根pivot := root.RightT2 := pivot.Leftpivot.Left = rootroot.Right = T2// 重新计算两个调整后的节点高度root.Height = max(height(root.Left), height(root.Right)) + 1pivot.Height = max(height(pivot.Left), height(pivot.Right)) + 1return pivot
}// 查找
func (t *AVLTree) Search(key int) *Node {return search(t.Root, key)
}func search(node *Node, key int) *Node {if node == nil {return nil}if key == node.Key {return node}if key < node.Key {return search(node.Left, key)}return search(node.Right, key)
}
3.2 插入操作
func (t *AVLTree) Insert(key int) {t.Root = insert(t.Root, key)
}func insert(node *Node, key int) *Node {// 1. 找到插入节点的位置if node == nil {return &Node{Key: key, Height: 1}}if key < node.Key {node.Left = insert(node.Left, key)} else if key > node.Key {node.Right = insert(node.Right, key)} else {//重复的key是不被允许的return node}// 2. 更新新插入节点的祖先节点的高度node.Height = max(height(node.Left), height(node.Right)) + 1// 3. 获得当前节点的平衡因子balance := getBalance(node)// 4. 平衡调整// 4.1说明新插入的节点插入到了当前节点的左节点的左孩子,需要进行右旋if balance > 1 && key < node.Left.Key {return rightRotate(node)}// 4.2说明新插入的节点插入到了当前节点的右节点的右孩子,需要进行左旋if balance < -1 && key > node.Right.Key {return leftRotate(node)}// 4.3说明新插入的节点插入到了当前节点的左节点的右孩子,需要进行左旋+右旋if balance > 1 && key > node.Right.Key {node.Left = leftRotate(node.Left)return rightRotate(node)}// 4.4说明新插入的节点插入到了当前节点的右节点的左孩子,需要进行右旋+左旋if balance < -1 && key < node.Left.Key {node.Right = rightRotate(node.Right)return leftRotate(node)}// 4.5 不要需要进行平衡调整return node
}
3.3 删除操作
func (t *AVLTree) Delete(key int) {t.Root = delete(t.Root, key)
}func delete(node *Node, key int) *Node {if node == nil {return nil}// 1. 找到要删除的节点if key < node.Key {node.Left = delete(node.Left, key)} else if key > node.Key {node.Right = delete(node.Right, key)} else {// 被删除的节点是叶子节点或者只有一个孩子节点if node.Left == nil {return node.Right} else if node.Right == nil {return node.Left}// 被删除的节点下面还有两个孩子节点// 先找到被删除节点下面最小的值temp := minValueNode(node.Right)// 将最小的值放到当前节点node.Key = temp.Key// 递归删除最小值node.Right = delete(node.Right, temp.Key)}if node == nil {return node}// 2. 更新新插入节点的祖先节点的高度node.Height = max(height(node.Left), height(node.Right)) + 1// 3. 获得当前节点的平衡因子balance := getBalance(node)// 4. 平衡调整// 4.1说明新删除的节点导致当前节点的平衡因子出了问题,// 判断是当前节点左节点的左孩子造成的,需要进行右旋if balance > 1 && getBalance(node.Left) >= 0 {return rightRotate(node)}// 4.2说明新删除的节点导致当前节点的平衡因子出了问题,// 判断是当前节点右节点的右孩子造成的,需要进行左旋if balance < -1 && getBalance(node.Right) <= 0 {return leftRotate(node)}// 4.3说明新删除的节点导致当前节点的平衡因子出了问题,// 判断是当前节点左节点的右孩子造成的,需要进行左旋+右旋if balance > 1 && getBalance(node.Left) < 0 {node.Left = leftRotate(node.Left)return rightRotate(node)}// 4.4说明新删除的节点导致当前节点的平衡因子出了问题,// 判断是当前节点右节点的左孩子造成的,需要进行右旋+左旋if balance < -1 && getBalance(node.Right) > 0 {node.Right = rightRotate(node.Right)return leftRotate(node)}// 4.5 不要需要进行平衡调整return node
}func minValueNode(node *Node) *Node {current := nodefor current.Left != nil {current = current.Left}return current
}
3.4 测试
func main() {tree := &AVLTree{}// 插入节点tree.Insert(10)tree.Insert(20)tree.Insert(30)tree.Insert(40)tree.Insert(50)tree.Insert(60)tree.Insert(70)// 层次遍历fmt.Println(LevelOrder(tree.Root))tree.Delete(10)tree.Delete(20)tree.Delete(30)fmt.Println(LevelOrder(tree.Root))
}// LevelOrder 返回层次遍历的结果(按层分组)
func LevelOrder(root *Node) [][]int {result := make([][]int, 0)if root == nil {return result}// 使用队列来存储节点queue := []*Node{root}for len(queue) > 0 {// 当前层的节点数levelSize := len(queue)// 存储当前层的值currentLevel := make([]int, 0, levelSize)// 遍历当前层的所有节点for i := 0; i < levelSize; i++ {// 获取队首节点node := queue[0]queue = queue[1:] // 出队// 将当前节点的值加入当前层的结果中currentLevel = append(currentLevel, node.Key)// 将子节点加入队列if node.Left != nil {queue = append(queue, node.Left)}if node.Right != nil {queue = append(queue, node.Right)}}// 将当前层的结果加入最终结果result = append(result, currentLevel)}return result
}
层次遍历的结果,符合预期

相关文章:

【计算机基础——数据结构——AVL平衡二叉树】
1. BST二叉查找树 1.1 BST二叉查找树的特性 左子树上所有结点的值均小于或等于它的根结点的值。右子树上所有结点的值均大于或等于它的根结点的值。左、右子树也分别为二叉排序树。 1.2 BST二叉查找树的缺点 二叉查找树是有缺点的,在不断插入的时候,…...
体育活动赛事报名马拉松微信小程序开发
功能描述 体育活动赛事报名马拉松微信小程序,该项目是一个体育活动报名小程序,主要功能有活动报名、扫码签到、签到积分、排行奖励、积分兑换等功能。 用户端🔶登录:◻️1.微信授权登录 ◻️2.手机号码授权 🔶首页&am…...

【C++】C++基础知识
一.函数重载 1.函数重载的概念 函数重载是函数的一种特殊情况,C允许在同一作用域中声明几个功能类似的同名函数,这些同名函数的形参列表必须不同。函数重载常用来处理实现功能类似,而数据类型不同的问题。 #include <iostream> using…...

中间件安全
IIS IIS短文件漏洞 此漏洞实际是由HTTP请求中旧DOS 8.3名称约定(SFN)的代字符(~)波浪号引起的。它允许远程攻击者在Web根目录下公开文件和文件夹名称(不应该可被访问)。攻击者可以找到通常无法从外部直接访问的重要文件,并获取有关应用程序基础结构的信息。 利用工具 https…...

Zabbix中文监控指标数据乱码
1)点击主机,选择Zabbix server 中的 图形 一项,可以看到当前显示的为乱码 2) 下载字体文件: https://gitcode.com/open-source-toolkit/4a3db/blob/main/SimHei.zip 解压unzip -x SimHei.zip 3) 替换字体文…...

【AI】AI如何赋能软件开发流程
方向一:流程与模式介绍【传统软件开发 VS AI参与的软件开发】 传统软件开发流程 传统软件开发流程一般可以分为以下几个阶段: 1. 需求分析:在这个阶段,开发团队与客户沟通,明确软件的需求和目标。团队会收集、整理和分…...

恒创科技:什么是 RAID 3 ? RAID 3、4 和5之间有什么区别?
RAID 是一种存储数据以提高性能并减少数据丢失的特定技术。您可以根据自己的需求选择多种 RAID 类型。RAID 3 是列表中比较有效的类型之一。本文将重点介绍这种特定的 RAID 技术,并比较 RAID 3、4 和 5。 RAID 3 的定义 RAID 3 是一种特定的磁盘配置,用于…...

python获取iOS最近业务日志的两种方法
当iOS UI自动化用例执行失败的时候,需要获取当时的业务日志,供后续分析使用。 现在已经把iOS沙盒目录挂载到本地,剩下的事情就是从沙盒目录中捞取当前的日志,沙盒中的日志文件较大,整体导出来也可以,但是会…...

【如何获取股票数据43】Python、Java等多种主流语言实例演示获取股票行情api接口之沪深指数历史交易数据获取实例演示及接口API说明文档
最近一两年内,股票量化分析逐渐成为热门话题。而从事这一领域工作的第一步,就是获取全面且准确的股票数据。因为无论是实时交易数据、历史交易记录、财务数据还是基本面信息,这些数据都是我们进行量化分析时不可或缺的宝贵资源。我们的主要任…...
:从零配置 ESLint)
ESLint 使用教程(一):从零配置 ESLint
前言 在现代前端开发中,代码质量和风格一致性是团队合作和项目维护的重要因素。而 ESLint 作为一款强大的 JavaScript 静态代码分析工具,能够帮助开发者发现和修复代码中的潜在问题。本文将详细介绍 ESLint 的常用规则配置,并结合实际应用场…...

openssl对称加密代码讲解实战
文章目录 一、openssl对称加密和非对称加密算法对比1. 加密原理2. 常用算法3. 加密速度4. 安全性5. 应用场景6. 优缺点对比综合分析 二、代码实战代码说明:运行输出示例代码说明:注意事项 一、openssl对称加密和非对称加密算法对比 OpenSSL 是一个广泛使…...

web前端动画按钮(附源代码)
效果图 源代码 HTML部分 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Document</title> …...

go函数传值是值传递?还是引用传递?slice案例加图解
先说下结论 Go语言中所有的传参都是值传递(传值),都是一个副本,一个拷贝。 值语义类型:参数传递的时候,就是值拷贝,这样就在函数中就无法修改原内容数据。 基本类型:byte、int、bool…...

PostgreSQL数据库笔记
PostgreSQL 是什么 PostgreSQL(简称Postgres或PG)是一个功能强大、可靠性高、可扩展性好的开源对象-关系数据库服务器(ORDBMS),它以加州大学伯克利分校计算机系开发的POSTGRES版本4.2为基础。 发展历程 起源与发展&a…...

财务软件源码SaaS云财务
在如今的商业环境中,准确的财务管理是一家企业取得成功的关键。然而,传统的财务管理方法已经无法满足现代企业的需求,需要一个全新的解决方案。推出了全新的财务软件为您提供完美的解决方案。 选择财务软件源码,您将享受到以下优…...

Elasticsearch集群和Kibana部署流程
搭建Elasticsearch集群 1. 进入Elasticsearch官网下载页面,下载Elasticsearch 在如下页面选择Elasticsearch版本,点击download按钮,进入下载页面 右键选择自己操作系统对应的版本,复制下载链接 然后通过wget命令下载Elastics…...

丹摩征文活动 | 丹摩智算:大数据治理的智慧引擎与实践探索
丹摩DAMODEL|让AI开发更简单!算力租赁上丹摩! 目录 一、引言 二、大数据治理的挑战与重要性 (一)数据质量问题 (二)数据安全威胁 (三)数据管理复杂性 三、丹摩智算…...

【Django】Clickjacking点击劫持攻击实现和防御措施
Clickjacking点击劫持 1、clickjacking攻击2、clickjacking攻击场景 1、clickjacking攻击 clickjacking攻击又称为点击劫持攻击,是一种在网页中将恶意代码等隐藏在看似无害的内容(如按钮)之下,并诱使用户点击的手段。 2、clickj…...
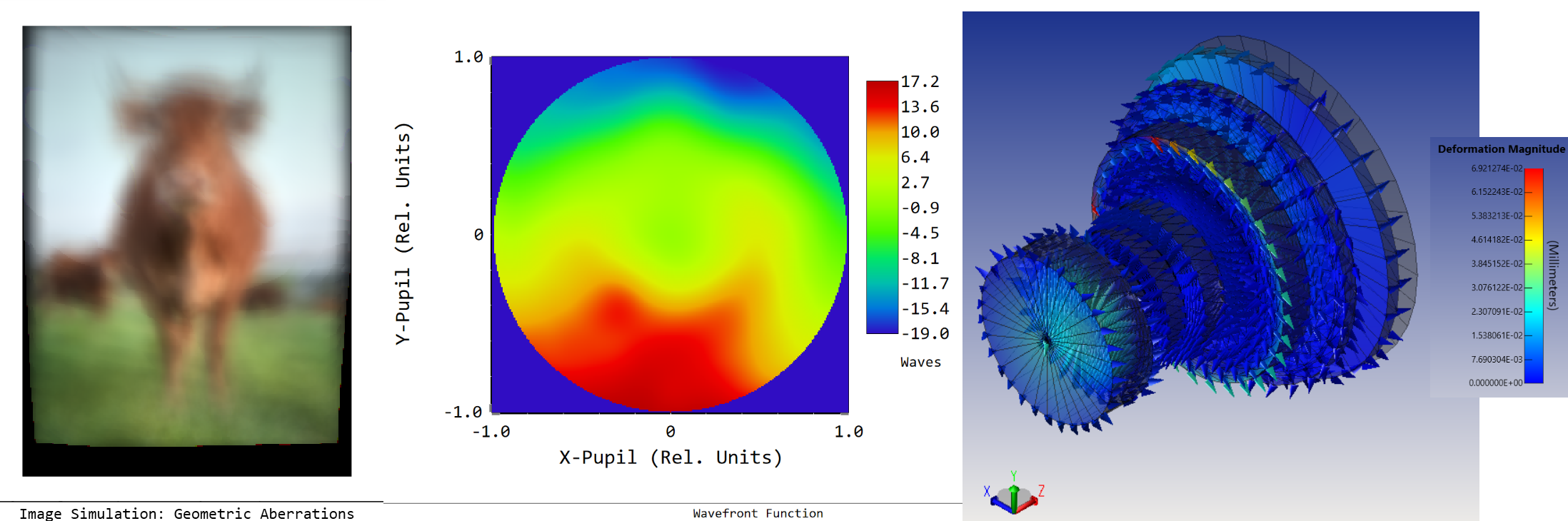
Ansys Zemax | 手机镜头设计 - 第 4 部分:用LS-DYNA进行冲击性能分析
该系列文章将讨论智能手机镜头模组设计的挑战,从概念和设计到制造和结构变形分析。本文是四部分系列中的第四部分,它涵盖了相机镜头的显式动态模拟,以及对光学性能的影响。使用Ansys Mechanical和LS-DYNA对相机在地板上的一系列冲击和弹跳过程…...

工具收集 - java-decompiler / jd-gui
工具收集 - java-decompiler / jd-gui 参考资料 用法:拖进来就行了 参考资料 https://github.com/java-decompiler/jd-gui 脚本之家:java反编译工具jd-gui使用详解...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

MySQL 主从同步异常处理
阅读原文:https://www.xiaozaoshu.top/articles/mysql-m-s-update-pk MySQL 做双主,遇到的这个错误: Could not execute Update_rows event on table ... Error_code: 1032是 MySQL 主从复制时的经典错误之一,通常表示ÿ…...
