数据结构--排序算法
目录
- 一.排序相关概念
- 二.常见排序算法
- 1.堆排序
- 2.插入排序
- 3.希尔排序
- 4.选择排序
- 5.冒泡排序
- 6.快速排序
- 1.快速排序--递归(未优化)
- 2.快速排序--递归(优化)
- 3.快速排序--非递归
- 7.归并排序
- 1.归并排序--递归
- 2.归并排序--非递归
一.排序相关概念
- 排序:使一串记录按照某个关键字的大小,递增或递减的排列起来
- 稳定性:在未排序的序列中,存在
多个具有相同关键字的记录,如果在经过排序之后,这些记录的相对次序保持不变,则称这种排序算法是稳定的 - 内部排序:数据元素全部放在内存中的排序
- 外部排序:相关元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序
二.常见排序算法
1.堆排序
- 基本思想:建立大/小根堆,将堆尾元素(end位置元素)与堆顶元素(堆中最大/小值)交换,调整end位置前的所有结点使其重新满足大/小根堆的性质,同时end位置向前移动,循环这个过程直至end位置移动堆顶位置(
每次都将堆的最大/小值移动到堆尾) - 时间复杂度:
O(NlogN) - 空间复杂度:
O(1) - 稳定性:不稳定
public void heapSort(int[] array) {createBigHeap(array);int end = array.length - 1;while (end > 0) {swap(array, 0, end);siftDown(array, 0, end);end--;}}public void createBigHeap(int[] array) {for (int parent = (array.length - 1 - 1) / 2; parent >= 0; parent--) {siftDown(array, parent, array.length);}}public void siftDown(int[] array, int parent, int end) {int child = 2 * parent + 1;while (child < end) {if (child + 1 < end && array[child] < array[child + 1]) {child++;}if (array[child] > array[parent]) {swap(array, child, parent);parent = child;child = 2 * parent + 1;} else {break;}}}public void swap(int[] array, int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}
2.插入排序
- 基本思想:把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中,直到所有的记录插入完为止,得到一个新的有序序列
- 时间复杂度:
O(N^2^) - 空间复杂度:
O(1) - 稳定性:稳定
- 特点:元素集合越接近
有序,插入排序算法的时间效率就越高
public void insertSort(int[] array) {for (int i = 1; i < array.length; i++) {int tmp = array[i];// 获取插入的元素int j = i - 1;for (; j >= 0; j--) { // 寻找要插入的位置if (array[j] > tmp) {array[j + 1] = array[j];} else {break;// 找到了要插入的位置或者没找到(j移动到-1位置)}}array[j + 1] = tmp;}}
3.希尔排序
- 基本思想:先选定一个整数gap,把待排序文件中所有记录
分成多个组,所有距离为gap的记录分在同一组内,并对每一组内的记录进行排序。然后,重复上述分组和排序的工作。当gap=1时,所有记录排序完成 - 时间复杂度:
约O(N^1.25^)~N(1.6*N^1.25^) - 空间复杂度:
O(1) - 稳定性:不稳定
public void shellSort(int[] array) {int gap = array.length;while (gap > 0) {gap = gap / 2;shell(array, gap);}}public void shell(int[] array, int gap) {for (int i = gap; i < array.length; i++) {int tmp = array[i];int j = i - gap;for (; j >= 0; j--) {if (array[j] > tmp) {array[j + gap] = array[j];} else {break;}}array[j + gap] = tmp;}}
4.选择排序
- 基本思想:每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的数据元素排完
- 时间复杂度:
O(N^2^) - 空间复杂度:
O(1) - 稳定性:不稳定
public void selectSort(int[] array) {for (int i = 0; i < array.length - 1; i++) {int minIndex = i;for (int j = i + 1; j < array.length; j++) {if (array[j] < array[minIndex]) {minIndex = j;}}swap(array, i, minIndex);}}public void swap(int[] array, int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;}
5.冒泡排序
- 基本思想:在待排序的数据元素中,将相邻的两个数进行比较,若前面的数比后面的数大就交换两数,否则不交换;循环这个过程,直至最终完成排序(
小的数据向前移动,大的数据向后移动) - 时间复杂度:
O(N^2^) - 空间复杂度:
O(1) - 稳定性:稳定
public void bubbleSort(int[] array) {for (int i = 0; i < array.length - 1; i++) {boolean flag = false;for (int j = 0; j < array.length - 1 - i; j++) {if (array[j] > array[j + 1]) {swap(array, j, j + 1);flag = true;}}if (!flag) {return;}}}
6.快速排序
- 基本思想:任取待排序元素序列中的某元素作为
基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上 - 时间复杂度:
O(NlogN) - 空间复杂度:
O(logN) - 稳定性:不稳定
1.快速排序–递归(未优化)
public void quickSort(int[] array) {quick(array, 0, array.length - 1);}public void quick(int[] array, int start, int end) {if (start >= end) {return;}int pivot = partition1(array, start, end);// 基准值下标// 左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值quick(array, start, pivot - 1);// 递归左子序列quick(array, pivot + 1, end);// 递归右子序列}// 将区间按照基准值划分为左右两半部分的常见方式:Hoare法和挖坑法// Hoare法public int partition1(int[] array, int left, int right) {// left和right分别为array子序列的最左和最右元素下标int tmp = array[left];// 基准值int start = left;while (left < right) {// right向前走,寻找<=基准值的元素下标while (left < right && array[right] >= tmp) {right--;}// left向后走,寻找>=基准值的元素下标while (left < right && array[left] <= tmp) {left++;}// 交换left和right下标的元素swap(array, left, right);}// left和right相遇,将基准值与相遇位置元素交换swap(array, start, left);return left;}// 挖坑法public int partition2(int[] array, int left, int right) {int tmp = array[left];// left下标元素填入tmp中,留下一个坑(left下标)while (left < right) {// right向前走,寻找<=基准值的元素下标while (left < right && array[right] >= tmp) {right--;}array[left] = array[right];// 填入坑(left下标)中,留下一个坑(right下标)// left向后走,寻找>=基准值的元素下标while (left < right && array[left] <= tmp) {left++;}array[right] = array[left];// 填入坑(right下标)中,留下一个坑(left下标)}// left和right相遇,将tmp填入相遇位置这个坑中array[left] = tmp;return left;}
2.快速排序–递归(优化)
- 三数取中法选key(减少划分区间时没有左/右子序列的情况)
- 递归到小的区间时,使用
插入排序
public void quickSort(int[] array) {quick(array, 0, array.length - 1);}public void quick(int[] array, int start, int end) {if (start >= end) {return;}if (start - end + 1 <= 10) { // 子序列长度较短时,使用插入排序insertSortSTE(array, start, end);return;}int mid = middle(array, start, end);// 获取中间值的下标swap(array, start, mid);// 交换start和mid下标元素,使得基准值为mid元素int pivot = partition1(array, start, end);quick(array, start, pivot - 1);quick(array, pivot + 1, end);}public int middle(int[] array, int left, int right) { // 三数取中法(left,mid,right)int mid = left + ((right - left) >> 1);int[] num = {array[left], array[mid], array[right]};Arrays.sort(num);if (array[left] == num[1]) {return left;} else if (array[right] == num[1]) {return right;} else {return mid;}}// 指定区间插入排序public void insertSortSTE(int[] array, int start, int end) {for (int i = start + 1; i <= end; i++) {int tmp = array[i];int j = i - 1;for (; j >= start; j--) {if (array[j] > tmp) {array[j + 1] = array[j];} else {break;}}array[j + 1] = tmp;}}
3.快速排序–非递归
public void quickSortNor(int[] array) {int left = 0;int right = array.length - 1;int pivot = partition1(array, left, right);Stack<Integer> stack = new Stack<>();if (pivot - 1 > left) {stack.push(left);stack.push(pivot - 1);}if (pivot + 1 < right) {stack.push(pivot + 1);stack.push(right);}while (!stack.isEmpty()) {right = stack.pop();left = stack.pop();pivot = partition1(array, left, right);if (pivot - 1 > left) {stack.push(left);stack.push(pivot - 1);}if (pivot + 1 < right) {stack.push(pivot + 1);stack.push(right);}}}
7.归并排序
- 基本思想:归并排序是建立在归并操作上的一种有效的排序算法,为分治法的一个典型应用,即将待排序的数据
分段排序后合并 - 时间复杂度:O(NlogN)
- 空间复杂度:O(N)
- 稳定性:稳定
1.归并排序–递归
public void mergeSort(int[] array) {branch(array, 0, array.length - 1);}public void branch(int[] array, int left, int right) {if (left >= right) {return;}int mid = left + ((right - left) >> 1);branch(array, left, mid);// 分解左子序列branch(array, mid + 1, right);// 分解右子序列merge(array, left, mid, right); // 合并子序列}public void merge(int[] array, int left, int mid, int right) {int s1 = left;int e1 = mid;int s2 = mid + 1;int e2 = right;int index = 0;int[] ans = new int[right - left + 1];while (s1 <= e1 && s2 <= e2) {if (array[s1] <= array[s2]) {ans[index++] = array[s1++];} else {ans[index++] = array[s2++];}}while (s1 <= e1) {ans[index++] = array[s1++];}while (s2 <= e2) {ans[index++] = array[s2++];}for (int i = left; i <= right; i++) {array[i] = ans[i - left];}}
2.归并排序–非递归
public void merge(int[] array, int left, int mid, int right) {int s1 = left;int e1 = mid;int s2 = mid + 1;int e2 = right;int index = 0;int[] ans = new int[right - left + 1];while (s1 <= e1 && s2 <= e2) {if (array[s1] <= array[s2]) {ans[index++] = array[s1++];} else {ans[index++] = array[s2++];}}while (s1 <= e1) {ans[index++] = array[s1++];}while (s2 <= e2) {ans[index++] = array[s2++];}for (int i = left; i <= right; i++) {array[i] = ans[i - left];}}public void mergeSortNor(int[] array) {int gap = 1;while (gap < array.length) {for (int i = 0; i < array.length; i++) {int left = i;int mid = left + gap - 1;if (mid >= array.length) {mid = array.length - 1;}int right = mid + gap;if (right >= array.length) {right = array.length - 1;}merge(array, left, mid, right);}gap *= 2;}}
相关文章:

数据结构--排序算法
目录 一.排序相关概念二.常见排序算法1.堆排序2.插入排序3.希尔排序4.选择排序5.冒泡排序6.快速排序1.快速排序--递归(未优化)2.快速排序--递归(优化)3.快速排序--非递归 7.归并排序1.归并排序--递归2.归并排序--非递归 一.排序相关概念 排序:使一串记录按照某个关…...
)
day60 图论章节刷题Part10(Floyd 算法、A * 算法)
Floyd 算法 思路:本题是多源最短路问题,使用Floyd算法求解。Floyd 算法对边的权值正负没有要求,核心思想是动态规划。 我们使用动规五部曲来理解和应用Floyd算法: 1、确定dp数组(dp table)以及下标的含义…...

UI架构解说
UI(用户界面,User Interface) 是指用户与软件或硬件系统进行交互的界面。 它是用户与系统之间的桥梁,允许用户通过视觉元素、交互组件和反馈机制来操作和控制应用程序或设备。 UI 设计的目标是提供直观、易用和愉悦的用户体验&a…...
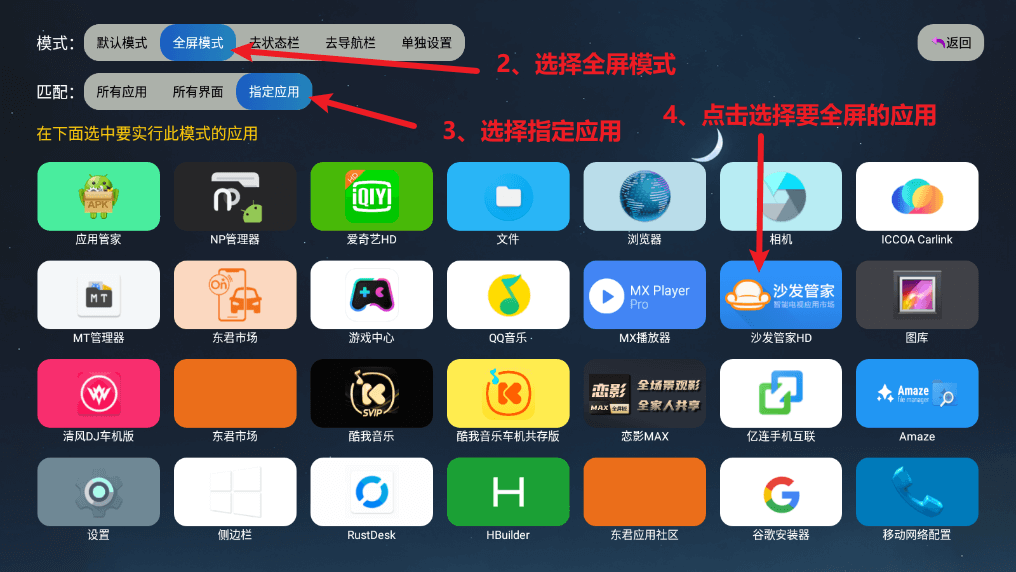
车机安装第三方软件实现打开软件全屏教程
简介 越来越多的车友实现安装第三方软件了,但是有的车机的状态栏或者导航栏会遮挡安装的第三方软件。这样的话,第三方软件就会显示不全,体验感非常不好。所以,下面我教一下大家如何使用东君应用管家来实现打开第三方软件全屏。 全…...
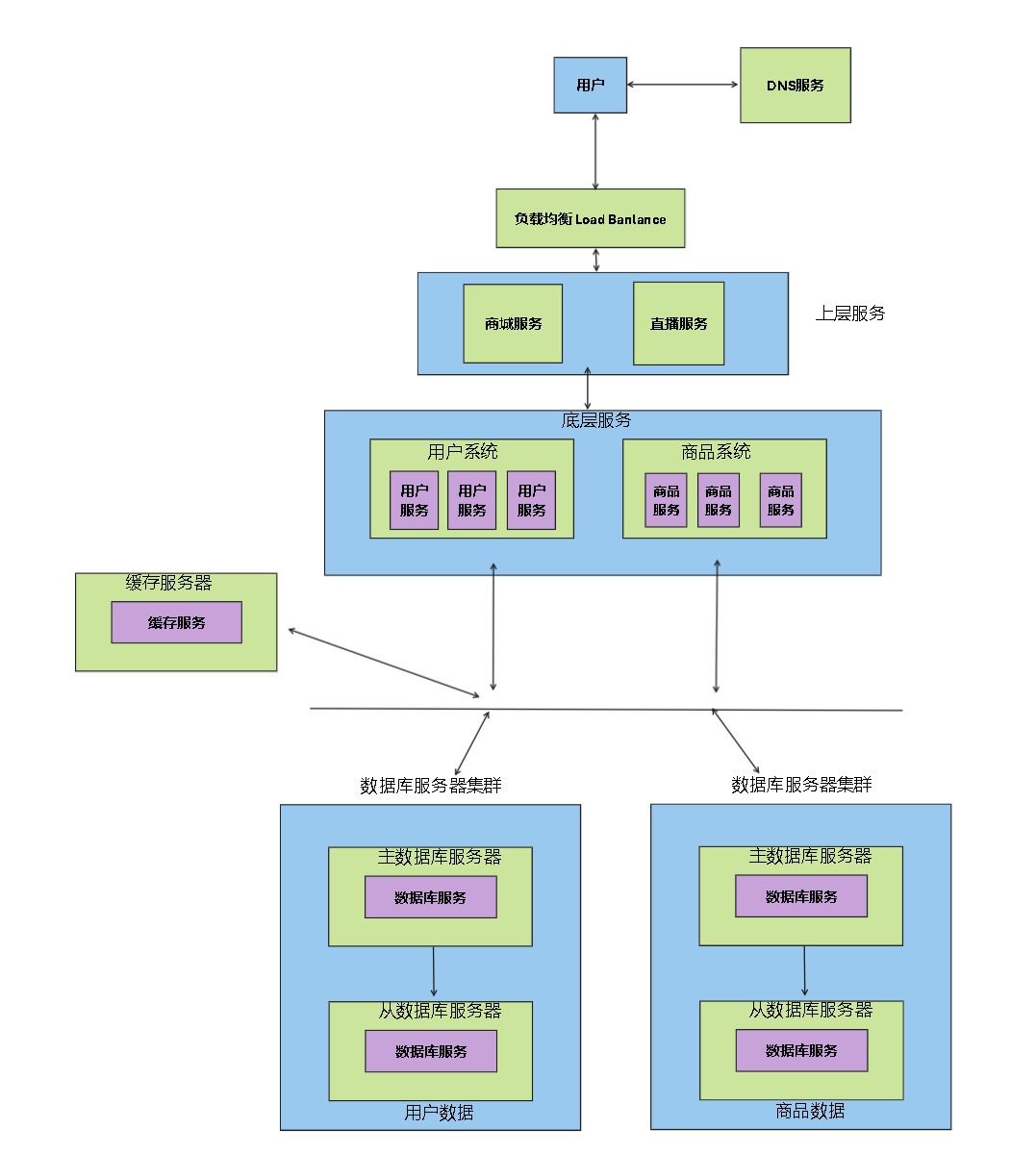
八大技术架构与演进2
垂直分库架构 当数据量不断增大,大量的数据都存储在一个库中就已经不太够用了,这时候就可以讲不同的数据分类别存储Mycat也支持在大表拆分为小标的情况下进行访问 但是这种做法其实是增加了数据库的运维难度,这种其实也就叫做分布式数据库&…...

ReactPress技术揭秘
ReactPress Github项目地址:https://github.com/fecommunity/reactpress 欢迎Star。 一、引言 ReactPress是一个基于React构建的开源发布平台,它不仅可以帮助用户在支持React和MySQL数据库的服务器上快速搭建自己的博客或网站,还能作为一个…...

Javascript高级—如何实现一个类型判断函数?
实现一个类型判断函数 判断null判断基础类型使用Object.prototype.toString.call(target)来判断引用类型 [!NOTE] 注意: 一定是使用call来调用,不然是判断的Object.prototype的类型 之所以要先判断是否为基本类型是因为:虽然Object.prototyp…...

asitop macOS 终端 性能监控
macOS 终端 性能监控 安装 pip python3 -m ensurepip# pip3 --version pip 21.2.4安装 asitop pip3 install asitop运行 sudo asitop参考 asitopgithub asitopHow to Install pip on Mac...

Unity学习笔记(4):人物和基本组件
文章目录 前言开发环境新增角色添加组件RigidBody 2D全局项目设置Edit 给地图添加碰撞体 总结 前言 今天不加班,有空闲时间。争取一天学一课,养成习惯 开发环境 Unity 6windows 11vs studio 2022Unity2022.2 最新教程《勇士传说》入门到进阶ÿ…...

【深圳大学/大学物理实验2】弗兰克-赫兹实验预习题参考
一、单选题 共 13 小题 共 78 分 1. (6分)第一栅极电压UG1、第二栅极电压UG2和减速电压UP的作用分别是( ) 学生答案:C √ A. 使电子加速,消除阴极电子散射,使电子减速 B. 产生并加速电子,使电子加速&…...

vue2.7.14 + vant + vue cli脚手架转vite启动运行问题记录
文章目录 前言方案一(借用插件转换)启动命令,转换方案一转换遇到的问题 方案二(手动调整)方案两者对比小结 前言 vue cli 脚手架转成vite启动 简单说说这个项目的一些底层基本结构哈,以及写这篇博客的目的…...

Java基础-内部类与异常处理
(创作不易,感谢有你,你的支持,就是我前行的最大动力,如果看完对你有帮助,请留下您的足迹) 目录 一、Java 内部类 什么是内部类? 使用内部类的优点 访问局部变量的限制 内部类和继承 内部…...

vue2或vue3的name属性有什么作用?
在 Vue.js(无论是 Vue 2 还是 Vue 3)中,组件的 name 属性有几个重要的用途。虽然它不是必须的,但在某些情况下非常有用。以下是 name 属性的一些主要作用: 1. 调试工具 Vue Devtools 和其他调试工具会使用组件的 nam…...

【FOC进阶日记】实战篇③ 电机关键数据采集方法
作者 | 量子君 微信公众号 | 极客工作室 【FOC进阶日记】专栏目录 第一章 实战篇① FOC与SVPWM详解 第二章 实战篇② 自发电控制算法 第三章 实战篇③ 电机关键数据采集方法 文章目录 前言一、M法(从路程入手):二、T法(从时间入手)三、M/T测速法:四、实现过程:总结前言…...

XSS安全基础
欢迎关注公众号【测试开发备忘录】,交流学习经验 XSS 类型: 反射型XSS:简单的把用户输入的数据“反射”给浏览器,将恶意链接嵌入,非持久; 存储型XSS:把用户输入的数据“存储”在服务端…...
)
【计网不挂科】计算机网络期末考试——【选择题&填空题&判断题&简述题】试卷(3)
前言 大家好吖,欢迎来到 YY 滴计算机网络 系列 ,热烈欢迎! 本章主要内容面向接触过C的老铁 本博客主要内容,收纳了一部门基本的计算机网络题目,供yy应对期中考试复习。大家可以参考 本章是去答案版本。带答案的版本在下…...

516.最长回文子序列
刷算法题: 第一遍:1.看5分钟,没思路看题解 2.通过题解改进自己的解法,并且要写每行的注释以及自己的思路。 3.思考自己做到了题解的哪一步,下次怎么才能做对(总结方法) 4.整理到自己的自媒体平台。 5.再刷重复的类…...

leetcode hot100【LeetCode 114.二叉树展开为链表】java实现
LeetCode 114.二叉树展开为链表 题目描述 给你二叉树的根结点 root ,请你将它展开为一个单链表: 展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。 展开后的单链表应该与…...

SpringMVC学习记录(二)之接收数据
SpringMVC学习记录(二)之接收数据 一、快速搭建SpringMVC框架1、配置分析2、准备项目3、Controller声明4、Spring MVC核心组件配置类5、SpringMVC环境搭建6、启动测试 二、SpringMVC接收数据1、访问路径设置1)精准路径匹配2)模糊路…...

C语言串讲-3之函数和数组
1.函数名是一个指针,保存函数地址入口。函数名是函数的入口地址。函数的入口地址称为函数指针。 2.传参--本质是创建副本 (1)实参与形参 (2)值传递,指针传递,引用传递 …...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...
