普林斯顿:LLM基于边际优化的梯度纠缠

📖标题:A Common Pitfall of Margin-based Language Model Alignment: Gradient Entanglement
🌐来源:arXiv, 2410.13828
🌟摘要
🔸从人类反馈中强化学习(RLHF)已成为对齐语言模型(LM)的主要方法,使其更有帮助,危害更小。RLHF的核心是使用基于裕度的损失进行偏好优化,该损失仅根据首选和非首选响应之间的差异来指定理想的LM行为。
🔸在本文中,我们发现了基于裕度的方法的一个常见陷阱——理想LM行为在首选和非首选响应上的规范不足,随着裕度的增加,这会导致两个意想不到的后果:(1)非首选(例如,不安全)响应的概率可能会增加,从而导致潜在的安全对齐失败。(2) 即使这些响应是理想的,首选响应的概率也可能降低。我们揭开了这些有问题行为背后的原因:基于边际的损失将首选概率的变化与被取消的概率的梯度联系起来,反之亦然,这通常会阻止首选概率在被取消的情况下增加,从而导致两种概率同步增加或减少。我们将这种基于边缘的目标固有的效应称为梯度纠缠。从形式上讲,我们推导出了一般基于边缘的对齐目标的条件,在这些条件下,梯度纠缠变得令人担忧:优选对数概率的梯度与解卷积对数概率的斜率之间的内积相对于单个梯度范数较大。
🔸我们从理论上研究了为什么在对齐语言模型时,这些内积会很大,并实证验证了我们的发现。我们框架的实证意义进一步扩展到解释各种偏好优化算法训练动态的重要差异,并提出潜在的算法设计,以缓解基于边际的方法的规格不足问题,从而改善语言模型对齐。
🛎️文章简介
🔸研究问题:基于边际的语言模型在对齐中会面临常见的梯度纠缠陷阱。
🔸主要贡献:论文揭示了梯度纠缠是边际目标中固有的问题,导致了选择和拒绝概率同步增加或减少,并提出了两种潜在的算法设计来缓解梯度纠缠效应。
📝重点思路
🔺相关工作
🔸RLHF:LLM提高其有用性和减轻危害性的主要方法,包括教学数据的监督微调和偏好的强化对齐。
🔸奖励模型:近期研究通过边际的偏好优化损失来直接优化语言模型,但会出现所选响应和拒绝响应的对数概率同步增加或减少。
🔸原因分析:只指定了选择和拒绝的对数概率之间边际的理想行为,即让正例高于负例,而非降低负例概率和提高正例概率。
🔺论文方案
🔸理论分析:论文推导了梯度内积的条件,理论分析在基于边际的目标函数中,选择和拒绝的对数概率的梯度纠缠效应,解释了为什么在某些情况下选择和拒绝的对数概率会同步增加或减少。
🔸合成设置实验:在合成设置中,论文理论证明了当选择和拒绝的响应共享更多相似的token时,它们的梯度内积会增加。同时,尽管句子级别的梯度内积可能很大且为正,但单个token级别的内积可以很小且为负。
🔸实证验证:通过实证验证了这些理论见解,发现DPO和R-DPO中选择和拒绝的对数概率倾向于同时减少,证明了梯度纠缠的存在。
🔸算法设计:基于理论和实证分析,提出了两种潜在的算法设计来缓解梯度纠缠效应,即成对归一化梯度下降和稀疏正则化的token掩码。
🔎分析总结
🔸梯度纠缠的存在:实验发现,在DPO和R-DPO中,选择和拒绝的对数概率倾向于同时减少,这证明了梯度纠缠的存在。
🔸梯度内积的影响:实验揭示了梯度内积是驱动梯度纠缠效应的关键量,当梯度内积较大时,选择和拒绝的对数概率会同步增加或减少。
🔸token级别的梯度动态:实验发现,显著的token(如“positive”/“negative”)在选择和拒绝的响应中最具对比性,表现出负的梯度相关性,防止了梯度纠缠;而那些非对比性的不显著token(如相同的token)由于其梯度的高相似性,导致了梯度纠缠。
🔸算法设计的有效性:提出的两种算法设计(成对归一化梯度下降和稀疏正则化的token掩码)可能有效缓解梯度纠缠效应。
💡个人观点
论文的核心是理论和实验分析当前偏好对齐方案导致的正负样本概率同步变化,将其定义为token语义层面的梯度纠缠,算是一种“奖励黑客”导致没有真正学到奖励。
🧩附录


相关文章:

普林斯顿:LLM基于边际优化的梯度纠缠
📖标题:A Common Pitfall of Margin-based Language Model Alignment: Gradient Entanglement 🌐来源:arXiv, 2410.13828 🌟摘要 🔸从人类反馈中强化学习(RLHF)已成为对齐语言模型…...

通俗易懂:什么是 Java 类加载?
文章目录 类加载过程的三个阶段一个简单的案例:类加载的工作原理使用这个类类加载的顺序类加载的特点类加载的好处总结推荐阅读文章 在 Java 中, 类加载是一种将我们写的 Java 类文件加载到内存中的过程,让 JVM(Java 虚拟机&…...

Dijkstra 算法的实现方案
下面是一个基于 Dijkstra 算法的实现方案,能够在 DEM(数字高程模型)数据上进行寻路,并满足以下需求: 使用 Qt C++ 编写; 规避 DEM 中的障碍物; 支持指定起点和终点; 使用 GDAL 库读取 DEM 文件; 输出路径到 TXT 文件; 输出的坐标为地理坐标(例如经纬度),而不是像…...
)
OpenGL 进阶系列07 - 阴影贴图(shadowmap )
一:概述: 在 OpenGL 中,Shadow Mapping(阴影贴图)是一种常用的实时阴影技术,用于渲染物体的阴影效果。这种方法通过生成光源视角下的深度贴图,再在场景渲染时使用它来判断物体是否被遮挡,从而实现阴影效果。下面是实现 Shadow Mapping 的基本步骤和相关知识。 二:绘制…...

【CAN介绍】【第一篇章】
1. CAN简介 • CAN 总线( Controller Area Network Bus )控制器局域网总线 • CAN 总线是由 BOSCH 公司开发的一种简洁易用、传输速度快、易扩展、可靠性高的串行通信总线,广泛应用于汽车、嵌入式、工业控制等领域 • CAN 总线特征࿱…...

【统计子矩阵——部分前缀和+双指针】
题目 代码 #include <bits/stdc.h> using namespace std; typedef long long ll; const int N 510; int s[N][N]; int main() {ios::sync_with_stdio(0);cin.tie(0);int n, m, k;cin >> n >> m >> k;for(int i 1; i < n; i)for(int j 1; j <…...

用正则表达式检查是IP否为内网地址
用正则表达式检查是ip否为内网地址 PHP function isIntranet($ip) {/* IPV4内网地址A 类10.0.0.0~10.255.255.255B 类172.16.0.0~172.31.255.255C 类192.168.0.0~192.168.255.255*/// 检查是否为 IPv4 内网地址if (preg_match(/^10\./, $ip…...

Leetcode刷题笔记14
136. 只出现一次的数字 136. 只出现一次的数字 - 力扣(LeetCode) 核心思想:按位异或运算 利用按位异或运算的性质来解决这个问题: 异或运算的性质: a ^ a 0:相同的数异或结果为0。 a ^ 0 a:…...

PHP图书绘本借阅管理系统小程序源码
📚 图书绘本借阅管理系统:打造孩子的阅读乐园 📚 🏷️ 引言:为什么我们需要图书绘本借阅管理系统? 在孩子的成长旅程中,阅读是不可或缺的一部分。然而,面对琳琅满目的图书和绘本&a…...

【JavaWeb】JavaWeb入门之XML详解
目录 1.XML介绍 1.1.XML概述 1.1.1.什么是XML 1.1.2.XML的作用 1.1.3.XML与HTML的比较 1.1.4.XML和properties(属性文件)比较 1.1.5.W3C组织 1.2.XML语法概述 1.2.1.XML文档展示 1.2.2.XML文档的组成部分 1.3.XML文档声明 1.3.1.什么是XML文…...

JS手写-this绑定实现
在 JavaScript 中,bind、call 和 apply 方法都可以用来改变函数的 this 指向。下面我们将分别实现这些方法的简单版本。 1. 实现 bind bind 方法创建一个新的函数,在调用时设置 this 值,并返回这个新的函数。 Function.prototype.myBind …...

【时间之外】IT人求职和创业应知【31】
目录 新闻一:2024年“秦创原沣东杯”陕西省科技工作者创新创业大赛颁奖仪式暨沣东新城机器人产业发展大会盛大启幕 新闻二:声网CEO赵斌:RTE将成为生成式AI时代AI Infra的关键部分 新闻三:“5G工业互联网”融合应用试点城市名单…...

如何使用ffmpeg命令行进行录屏
录屏软件,我们去网上下载,发现有很多软件都是要收费的!但是录屏功能很难做吗?为啥都需要收费呢? 于是我整了个小demo,用于实现基础的屏幕录制功能。 思路很简单,考虑到 FFMpeg.exe是一个非常成…...

ODOO学习笔记(8):模块化架构的优势
灵活性与可定制性 业务流程适配:企业的业务流程往往因行业、规模和管理方式等因素而各不相同。Odoo的模块化架构允许企业根据自身的具体业务流程,选择和组合不同的模块。例如,一家制造企业可以启用采购、库存、生产和销售模块,并通…...

数字IC后端实现之Innovus specifyCellEdgeSpacing和ICC2 set_placement_spacing_rule的应用
昨天帮助社区IC训练营学员远程协助解决一个Calibre DRC案例。通过这个DRC Violation向大家分享下Innovus和ICC2中如何批量约束cell的spacing rule。 数字IC后端手把手实战教程 | Innovus verify_drc VIA1 DRC Violation解析及脚本自动化修复方案 下图所示为T12nm A55项目的Ca…...

每日小练:Day2
1.乒乓球筐 题目链接:乒乓球筐__牛客网 题目描述: 这道题主要考察B盒是不是A盒的子集,我们可以通过哈希表来做 单哈希表 import java.util.Scanner;// 注意类名必须为 Main, 不要有任何 package xxx 信息 public class Main {public stat…...

ubuntu 安装kafka-eagle
上传压缩包 kafka-eagle-bin-2.0.8.tar.gz 到集群 /root/efak 目录 cd /root/efak tar -zxvf kafka-eagle-bin-2.0.8.tar.gz cd /root/efak/kafka-eagle-bin-2.0.8 mkdir /root/efakmodule tar -zxvf efak-web-2.0.8-bin.tar.gz -C /root/efakmodule/ mv /root/efakmodule/efak…...

深入理解指针
在初步了解了指针的用法之后,我们可以想一想,既然一个变量有地址,而且在上一篇文章中我们知道了一个数组也有地址,那么函数、字符串这些东西有没有地址呢?如果有,那这些地址有什么用?我们又要怎…...
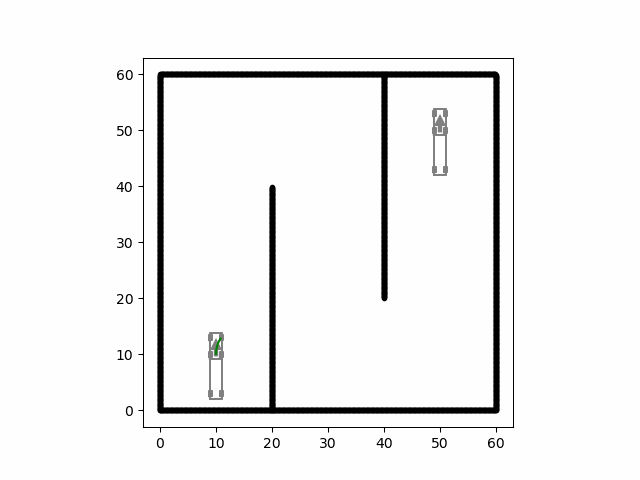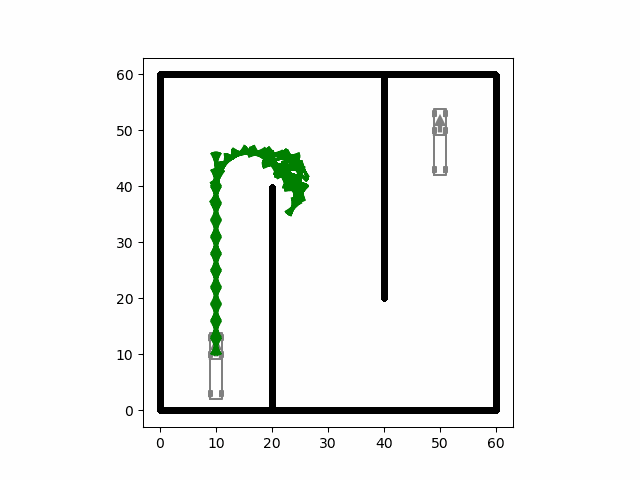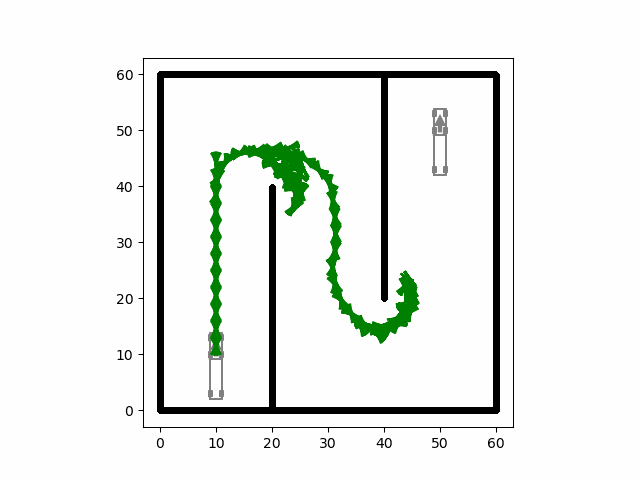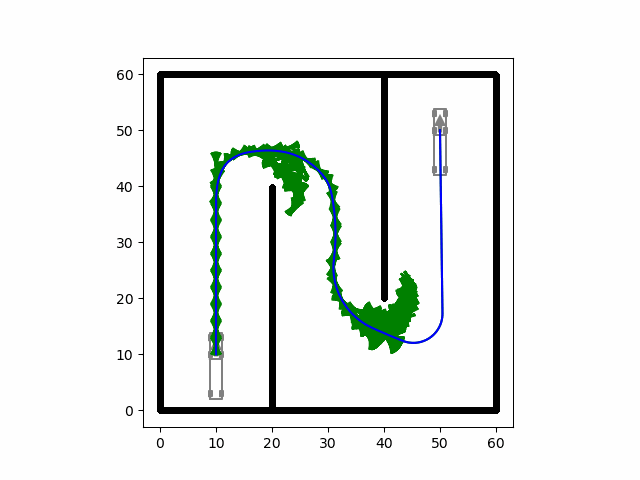
自动驾驶合集(更新中)
文章目录 车辆模型控制路径规划 车辆模型 车辆模型基础合集 控制 控制合集 路径规划 规划合集...

Chapter 14 scoped样式以及data函数
欢迎大家订阅【Vue2Vue3】入门到实践 专栏,开启你的 Vue 学习之旅! 文章目录 1 scoped样式1.1 全局样式1.2 局部样式1.3 工作原理2 data函数 1 scoped样式 1.1 全局样式 全局样式是指作用于整个应用程序的样式,不论在哪个组件中定义&#x…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...
