【C++融会贯通】二叉树进阶
目录
一、内容说明
二、二叉搜索树
2.1 二叉搜索树概念
2.2 二叉搜索树操作
2.2.1 二叉搜索树的查找
2.2.2 二叉搜索树的插入
2.2.3 二叉搜索树的删除
2.3 二叉搜索树的实现
2.3.1 二叉搜索树的节点设置
2.3.2 二叉搜索树的查找函数
2.3.2.1 非递归实现
2.3.2.2 递归实现
2.3.3 二叉搜索树的插入函数
2.3.3.1 非递归实现
2.3.4 二叉搜索树的中序遍历
2.3.5 二叉搜索树的删除函数
2.3.5.1 非递归实现当我们需要删除一个节点时找到删除节点,需要记录当前节点的父亲节点,防止删除的当前节点时,防止当前的节点的父亲节点中的指针变为野指针
2.3.6 二叉搜索树代码的整体实现
2.4 二叉搜索树的应用
2.5 二叉搜索树的性能分析
结尾

一、内容说明
二叉树在前面C数据结构阶段已经讲过:非线性表之堆的实际应用和二叉树的遍历-CSDN博客
- map和set特性需要先铺垫二叉搜索树,而二叉搜索树也是一种树形结构
- 二叉搜索树的特性了解,有助于更好的理解map和set的特性
- 二叉树中部分面试题稍微有点难度,在前面讲解大家不容易接受,且时间长容易忘
- 有些OJ题使用C语言方式实现比较麻烦,比如有些地方要返回动态开辟的二维数组,非常麻烦。
此次二叉树是为后面map和set的实现做铺垫,也是对二叉树进行收尾。
二、二叉搜索树
2.1 二叉搜索树概念
二叉搜索树又称二叉排序树,它或者是一棵空树,或者是具有以下性质的二叉树:
- 若它的左子树不为空,则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空,则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树

2.2 二叉搜索树操作

2.2.1 二叉搜索树的查找
- a、从根开始比较,查找,比根大则往右边走查找,比根小则往左边走查找。
- b、最多查找高度次,走到到空,还没找到,这个值不存在。
2.2.2 二叉搜索树的插入
插入的具体过程如下:
- a. 树为空,则直接新增节点,赋值给root指针
- b. 树不空,按二叉搜索树性质查找插入位置,插入新节点

2.2.3 二叉搜索树的删除
首先查找元素是否在二叉搜索树中,如果不存在,则返回, 否则要删除的结点可能分下面四种情 况:
- a. 要删除的结点无孩子结点
- b. 要删除的结点只有左孩子结点
- c. 要删除的结点只有右孩子结点
- d. 要删除的结点有左、右孩子结点
看起来有待删除节点有4中情况,实际情况a可以与情况b或者c合并起来,因此真正的删除过程 如下:
- 情况b:删除该结点且使被删除节点的双亲结点指向被删除节点的左孩子结点--直接删除

- 情况c:删除该结点且使被删除节点的双亲结点指向被删除结点的右孩子结点--直接删除

- 情况d:在它的右子树中寻找中序下的第一个结点(关键码最小),用它的值填补到被删除节点中,再来处理该结点的删除问题--替换法删除

2.3 二叉搜索树的实现
2.3.1 二叉搜索树的节点设置
template<class K>
struct BSTreeNode
{K _val;BSTreeNode<K>* _left;BSTreeNode<K>* _right;BSTreeNode(const K& val):_val(val),_left(nullptr),_right(nullptr){}
};2.3.2 二叉搜索树的查找函数
- 从根节点开始查找,若查找值比根节点小,继续向左子树寻找,若查找值比根节点大,继续向右子树寻找。
- 最多查找高度次,若查找到空,那么在这棵树中没有这个值,返回false。
2.3.2.1 非递归实现
template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public:bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_val > key){cur = cur->_left;}else if(cur->_val < key){cur = cur->_right;}else{return true;}}return false;}
private:// 成员变量Node* _root = nullptr;
};
2.3.2.2 递归实现
template<class K>
class BSTree
{typedef BSTreeNode<K> Node;
public:bool FindR(const K& key)//使用递归查找{return _FindR(_root, key);}
private:bool _FindR(Node* _root,const K& key){if (_root == nullptr)return false;if (_root->_val > key){return _FindR(_root->_left, key);}else if (_root->_val < key){return _FindR(_root->_right, key);}else{return true;}}
private:Node* _root;
};2.3.3 二叉搜索树的插入函数
- 若树为空,创建一个节点,赋值给root。
- 若树不为空,按照二叉搜索树的性质查找插入位置,插入新节点
2.3.3.1 非递归实现
//插入
bool Insert(const K& key)
{Node* cur = _root;Node* parent = nullptr;if (_root == nullptr){Node* newnode = new Node(key);_root = newnode;}else{while (cur){if (cur->_val > key){parent = cur;cur = cur->_left;}else if (cur->_val < key){parent = cur;cur = cur->_right;}else{return false;}}Node* newnode = new Node(key);if (parent->_val > key){parent->_left = newnode;}else{parent->_right = newnode;}}return true;
}2.3.3.2 递归实现
bool InsertR(const K& key)//使用递归插入
{return _InsertR(_root, key);
}bool _InsertR(Node*& root, const K& key)
{if (root == nullptr){root = new Node(key);return true;}if (root->_val < key){return _InsertR(root->_right, key);}else if (root->_val > key){return _InsertR(root->_left, key);}else{return false;}
}2.3.4 二叉搜索树的中序遍历
二叉树的中序遍历是:先递归遍历左子树,再访问根节点,最后递归遍历右子树。
void InOrder()
{_InOrder(_root);cout << endl;
}void _InOrder(Node* cur)
{ //递归的形式遍历if (cur == nullptr)return;_InOrder(cur->_left);cout << cur->_val << " ";_InOrder(cur->_right);
}2.3.5 二叉搜索树的删除函数
2.3.5.1 非递归实现
当我们需要删除一个节点时找到删除节点,需要记录当前节点的父亲节点,防止删除的当前节点时,防止当前的节点的父亲节点中的指针变为野指针
bool Erase(const K& key)
{Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_val > key){parent = cur;cur = cur->_left;}else if (cur->_val < key){parent = cur;cur = cur->_right;}else//找到了需要找的值{if (cur->_left == nullptr)//左为空{if (parent == nullptr)//删除结点为根结点{_root = cur->_right;}else{if (parent->_right == cur){parent->_right = cur->_right;}else{parent->_left = cur->_right;}}}//右为空else if (cur->_right == nullptr){if (parent == nullptr)//删除结点为根结点{_root = cur->_left;}else{if (parent->_right == cur){parent->_right = cur->_left;}else{parent->_left = cur->_left;}}}//左右不为空else{Node* parent = cur;Node* leftmax = cur->_left;while (leftmax->_right){parent = leftmax;leftmax = leftmax->_right;}swap(cur->_val, leftmax->_val);if (parent->_left == leftmax){parent->_left = leftmax->_left;}else{parent->_right = leftmax->_left;}cur = leftmax;}delete cur;return true;}}return false;
}2.3.6.2 递归实现
这里bool _EraseR(Node*& root, const K& key)中&的作用也是通过改变当前节点直接改变父亲节点的指向。
bool EraseR(const K& key)//使用递归删除
{return _EraseR(_root, key);
}
bool _EraseR(Node* root, const K& key)
{if (root == nullptr)return false;if (root->_val > key){_EraseR(root->_left, key);}else if (root->_val < key){_EraseR(root->_right, key);}else{Node* del = root;if (root->_left == nullptr){root = root->_right;}else if (root->_right == nullptr){root = root->_left;}else{Node* leftMax = root->_left;while (leftMax->_right){leftMax = leftMax->_right;}swap(root->_key, leftMax->_key);return _EraseR(root->_left, key);}delete del;return true;}
}2.3.6 二叉搜索树代码的整体实现
namespace lxp
{template<class K>struct BSTreeNode{K _val;BSTreeNode<K>* _left;BSTreeNode<K>* _right;BSTreeNode(const K& val):_val(val),_left(nullptr),_right(nullptr){}};template<class K>class BSTree{typedef BSTreeNode<K> Node;public:BSTree():_root(nullptr){}BSTree(const BSTree<K>& t){_root = Copy(t._root);}BSTree<K>& operator=(BSTree<K> t){swap(_root, t._root);return *this;}~BSTree(){Destroy(_root);}//插入bool Insert(const K& key){Node* cur = _root;Node* parent = nullptr;if (_root == nullptr){Node* newnode = new Node(key);_root = newnode;}else{while (cur){if (cur->_val > key){parent = cur;cur = cur->_left;}else if (cur->_val < key){parent = cur;cur = cur->_right;}else{return false;}}Node* newnode = new Node(key);if (parent->_val > key){parent->_left = newnode;}else{parent->_right = newnode;}}return true;}bool Find(const K& key){Node* cur = _root;while (cur){if (cur->_val > key){cur = cur->_left;}else if(cur->_val < key){cur = cur->_right;}else{return true;}}return false;}bool Erase(const K& key){Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_val > key){parent = cur;cur = cur->_left;}else if (cur->_val < key){parent = cur;cur = cur->_right;}else//找到了需要找的值{if (cur->_left == nullptr)//左为空{if (parent == nullptr)//删除结点为根结点{_root = cur->_right;}else{if (parent->_right == cur){parent->_right = cur->_right;}else{parent->_left = cur->_right;}}}//右为空else if (cur->_right == nullptr){if (parent == nullptr)//删除结点为根结点{_root = cur->_left;}else{if (parent->_right == cur){parent->_right = cur->_left;}else{parent->_left = cur->_left;}}}//左右不为空else{Node* parent = cur;Node* leftmax = cur->_left;while (leftmax->_right){parent = leftmax;leftmax = leftmax->_right;}swap(cur->_val, leftmax->_val);if (parent->_left == leftmax){parent->_left = leftmax->_left;}else{parent->_right = leftmax->_left;}cur = leftmax;}delete cur;return true;}}return false;}void InOrder(){_InOrder(_root);cout << endl;}void _InOrder(Node* cur){ //递归的形式遍历if (cur == nullptr)return;_InOrder(cur->_left);cout << cur->_val << " ";_InOrder(cur->_right);}bool FindR(const K& key)//使用递归查找{return _FindR(_root, key);}bool InsertR(const K& key)//使用递归插入{return _InsertR(_root, key);}bool EraseR(const K& key)//使用递归删除{return _EraseR(_root, key);}private:Node* Copy(Node* root){if (root == nullptr)return nullptr;Node* copyroot = new Node(root->_val);copyroot->_left = Copy(root->_left);copyroot->_right = Copy(root->_right);return copyroot;}void Destroy(Node*& root){if (root == nullptr)return;Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}bool _EraseR(Node* root, const K& key){if (root == nullptr)return false;if (root->_val > key){_EraseR(root->_left, key);}else if (root->_val < key){_EraseR(root->_right, key);}else{Node* del = root;if (root->_left == nullptr){root = root->_right;}else if (root->_right == nullptr){root = root->_left;}else{Node* leftMax = root->_left;while (leftMax->_right){leftMax = leftMax->_right;}swap(root->_key, leftMax->_key);return _EraseR(root->_left, key);}delete del;return true;}}bool _InsertR(Node*& root, const K& key){if (root == nullptr){root = new Node(key);return true;}if (root->_val < key){return _InsertR(root->_right, key);}else if (root->_val > key){return _InsertR(root->_left, key);}else{return false;}}bool _FindR(Node* _root,const K& key){if (_root == nullptr)return false;if (_root->_val > key){return _FindR(_root->_left, key);}else if (_root->_val < key){return _FindR(_root->_right, key);}else{return true;}}private:Node* _root;};
}2.4 二叉搜索树的应用
1. K模型:K模型即只有key作为关键码,结构中只需要存储Key即可,关键码即为需要搜索到的值。
比如:给一个单词word,判断该单词是否拼写正确,具体方式如下:
- 以词库中所有单词集合中的每个单词作为key,构建一棵二叉搜索树
- 在二叉搜索树中检索该单词是否存在,存在则拼写正确,不存在则拼写错误。
2. KV模型:每一个关键码key,都有与之对应的值Value,即的键值对。该种方式在现实生活中非常常见:
- 比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文就构成一种键值对;
- 再比如统计单词次数,统计成功后,给定单词就可快速找到其出现的次数,单词与其出现次数就是就构成一种键值对。
template<class K, class V>
struct BSTreeNode
{BSTreeNode<K, V>* _left;BSTreeNode<K, V>* _right;K _key;V _value;BSTreeNode(const K& key, const V& value):_key(key), _value(value), _left(nullptr), _right(nullptr){}
};template<class K, class V>
class BSTree
{typedef BSTreeNode<K, V> Node;
public: bool Insert(const K& key, const V& value){// 树为空则,该节点为根if (_root == nullptr){_root = new Node(key, value);return true;}Node* cur = _root;Node* prev = nullptr;while (cur){prev = cur;// 当当前节点的值大于要插入的值,那么向左找if (cur->_key > key){cur = cur->_left;}// 当当前节点的值小于要插入的值,那么向右找else if (cur->_key < key){cur = cur->_right;}// 二叉搜索树不允许相同的值存在,当这个值已经存在过了,那么返回false,即插入失败else{return false;}}if (prev->_key > key){prev->_left = new Node(key, value);return true;}else{prev->_right = new Node(key, value);return true;}return false;} Node* Find(const K& key){Node* cur = _root;while (cur){if (cur->_key > key){cur = cur->_left;}else if (cur->_key < key){cur = cur->_right;}// 找得到else{return cur;}}// 找不到return nullptr;}// 删除,非递归版本bool Erase(const K& key){Node* cur = _root;Node* prev = nullptr;// 找到需要删除的节点while (cur){if (cur->_key > key){prev = cur;cur = cur->_left;}else if (cur->_key < key){prev = cur;cur = cur->_right;}else{break;}}// 当当前根节点的左树为空时,那么链接右边if (cur->_left == nullptr){if (cur == _root){_root = cur->_left;delete cur;return true;}else{if (prev->_left == cur)prev->_left = cur->_right;elseprev->_right = cur->_right;delete cur;cur = nullptr;return true;}}// 当当前根节点的右树为空时,那么链接左边else if (cur->_right == nullptr){if (cur == _root){_root = cur->_left;delete cur;return true;}else{if (prev->_left == cur)prev->_left = cur->_left;elseprev->_right = cur->_left;delete cur;cur = nullptr;return true;}}else{prev = cur;Node* del = cur->_right;while (del->_left != nullptr){prev = del;del = del->_left;}swap(del->_key, cur->_key);if (prev->_left == del)prev->_left = del->_right;elseprev->_right = del->_right;delete del;del = nullptr;return true;}return false;}void InOrder(){_InOrder(_root);cout << endl;}~BSTree(){Destory(_root);}BSTree() {}BSTree(const BSTree<K, V>& T){_root = Copy(T._root);}BSTree<K, V>& operator=(BSTree<K, V> T){swap(_root, T._root);return *this;}private:Node* Copy(Node* Troot){if (Troot == nullptr)return nullptr;Node* root = new Node(Troot->_key);root->_left = Copy(Troot->_left);root->_right = Copy(Troot->_right);return root;}void Destory(Node*& root){if (root == nullptr)return;Destory(root->_left);Destory(root->_right);delete root;root = nullptr;}bool _InsertR(Node*& root, const K& key){if (root == nullptr){root = new Node(key);return true;}if (root->_key > key)return _InsertR(root->_left, key);else if (root->_key < key)return _InsertR(root->_right, key);// 出现相同的数字,返回falseelsereturn false;}void _InOrder(Node* root){if (root == nullptr)return;_InOrder(root->_left);cout << root->_key << ':' << root->_value << endl;_InOrder(root->_right);}Node* _root = nullptr;
};void TestBSTree()
{BSTree<string, string> dict;dict.Insert("insert", "插入");dict.Insert("erase", "删除");dict.Insert("left", "左边");dict.Insert("string", "字符串");dict.InOrder();string str;while (cin >> str){auto ret = dict.Find(str);if (ret){cout << str << ":" << ret->_value << endl;}else{cout << "单词拼写错误" << endl;}}string strs[] = { "苹果", "西瓜", "苹果", "樱桃", "苹果", "樱桃", "苹果", "樱桃", "苹果" };// 统计水果出现的次BSTree<string, int> countTree;for (auto str : strs){auto ret = countTree.Find(str);if (ret == NULL){countTree.Insert(str, 1);}else{ret->_value++;}}countTree.InOrder();
}
2.5 二叉搜索树的性能分析
插入和删除操作都必须先查找,查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树,若每个元素查找的概率相等,则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数,即结点越深,则比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树:

最优情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为:logN(log以2为底N的对数)
最差情况下,二叉搜索树退化为单支树(或者类似单支),其平均比较次数为:N
问题:如果退化成单支树,二叉搜索树的性能就失去了。那能否进行改进,不论按照什么次序插 入关键码,二叉搜索树的性能都能达到最优?那么我们后续章节学习的AVL树和红黑树就可以上场了。
结尾
如果有什么建议和疑问,或是有什么错误,希望大家可以在评论区提一下。
希望大家以后也能和我一起进步!!
如果这篇文章对你有用的话,请大家给一个三连支持一下!!
谢谢大家收看🌹🌹
相关文章:
【C++融会贯通】二叉树进阶
目录 一、内容说明 二、二叉搜索树 2.1 二叉搜索树概念 2.2 二叉搜索树操作 2.2.1 二叉搜索树的查找 2.2.2 二叉搜索树的插入 2.2.3 二叉搜索树的删除 2.3 二叉搜索树的实现 2.3.1 二叉搜索树的节点设置 2.3.2 二叉搜索树的查找函数 2.3.2.1 非递归实现 2.3.2.2 递…...

使用python-Spark使用的场景案例具体代码分析
使用场景 1. 数据批处理 • 日志分析:互联网公司每天会产生海量的服务器日志,如访问日志、应用程序日志等。Spark可以高效地读取这些日志文件,对数据进行清洗(例如去除无效记录、解析日志格式)、转换(例如…...

如何查看本地的个人SSH密钥
1.确保你的电脑上安装了 Git。 你可以通过终端或命令提示符输入以下命令来检查: git --version 如果没有安装,请前往 Git 官网 下载并安装适合你操作系统的版本。 2.查找SSH密钥 默认情况下,SSH密钥存储在你的用户目录下的.ssh文件夹中。…...

本人认为 写程序的三大基本原则
1. 合法性 定义:合法性指的是程序必须遵守法律法规和道德规范,不得用于非法活动。 建议: 了解法律法规:在编写程序之前,了解并遵守所在国家或地区的法律法规,特别是与数据隐私、版权、网络安…...
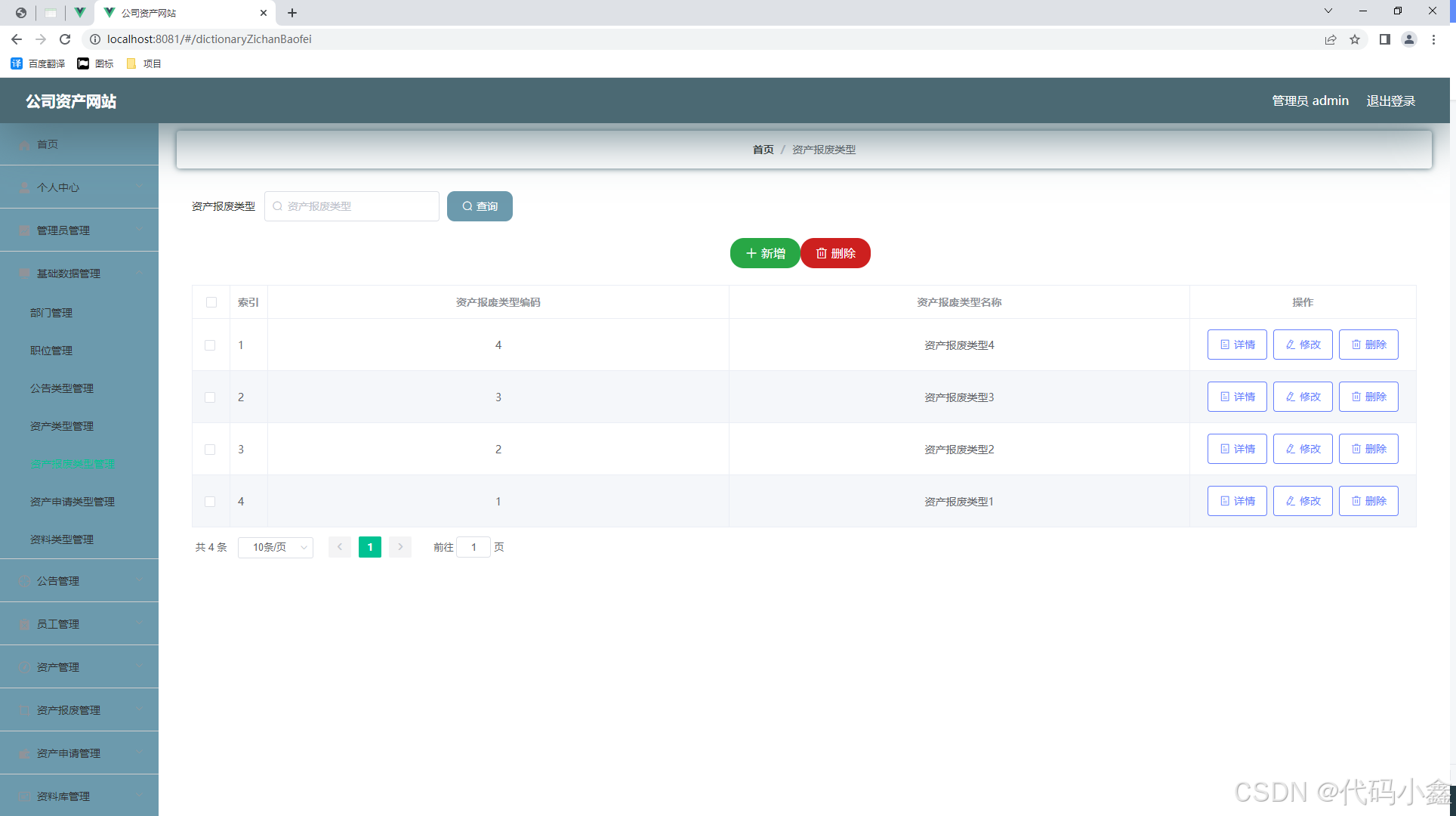
A030-基于Spring boot的公司资产网站设计与实现
🙊作者简介:在校研究生,拥有计算机专业的研究生开发团队,分享技术代码帮助学生学习,独立完成自己的网站项目。 代码可以查看文章末尾⬇️联系方式获取,记得注明来意哦~🌹 赠送计算机毕业设计600…...

React Hooks 深度解析与实战
💓 博客主页:瑕疵的CSDN主页 📝 Gitee主页:瑕疵的gitee主页 ⏩ 文章专栏:《热点资讯》 React Hooks 深度解析与实战 React Hooks 深度解析与实战 React Hooks 深度解析与实战 引言 什么是 Hooks? 定义 为什么需要 Ho…...

#渗透测试#SRC漏洞挖掘#蓝队基础之网络七层杀伤链04 终章
网络杀伤链模型(Kill Chain Model)是一种用于描述和分析网络攻击各个阶段的框架。这个模型最初由洛克希德马丁公司提出,用于帮助企业和组织识别和防御网络攻击。网络杀伤链模型将网络攻击过程分解为多个阶段,每个阶段都有特定的活…...

计算机毕业设计Python+大模型农产品推荐系统 农产品爬虫 农产品商城 农产品大数据 农产品数据分析可视化 PySpark Hadoop
温馨提示:文末有 CSDN 平台官方提供的学长联系方式的名片! 温馨提示:文末有 CSDN 平台官方提供的学长联系方式的名片! 温馨提示:文末有 CSDN 平台官方提供的学长联系方式的名片! 作者简介:Java领…...

爬虫补环境案例---问财网(rpc,jsdom,代理,selenium)
目录 一.环境检测 1. 什么是环境检测 2.案例讲解 二 .吐环境脚本 1. 简介 2. 基础使用方法 3.数据返回 4. 完整代理使用 5. 代理封装 6. 封装所有使用方法 jsdom补环境 1. 环境安装 2. 基本使用 3. 添加参数形式 Selenium补环境 1. 简介 2.实战案例 1. 逆向目…...

SpringBoot有几种获取Request对象的方法
HttpServletRequest 简称 Request,它是一个 Servlet API 提供的对象,用于获取客户端发起的 HTTP 请求信息。例如:获取请求参数、获取请求头、获取 Session 会话信息、获取请求的 IP 地址等信息。 那么问题来了,在 Spring Boot 中…...

在 Windows 11 中使用 MuMu 模拟器 12 国际版配置代理
**以下是优化后的教学内容,使用 Markdown 格式,便于粘贴到 CSDN 或其他支持 Markdown 格式的编辑器中: 在 Windows 11 中使用 MuMu 模拟器 12 国际版配置代理 MuMu 模拟器内有网络设置功能,可以直接在模拟器中配置代理。但如果你不确定如何操作,可以通过在 Windows 端设…...
ASP.NET Core Webapi 返回数据的三种方式
ASP.NET Core为Web API控制器方法返回类型提供了如下几个选择: Specific type IActionResult ActionResult<T> 1. 返回指定类型(Specific type) 最简单的API会返回原生的或者复杂的数据类型(比如,string 或者…...

SQL面试题——蚂蚁SQL面试题 连续3天减少碳排放量不低于100的用户
连续3天减少碳排放量不低于100的用户 这是一道来自蚂蚁的面试题目,要求我们找出连续3天减少碳排放量低于100的用户,之前我们分析过两道关于连续的问题了 SQL面试题——最大连续登陆问题 SQL面试题——球员连续四次得分 这两个问题都是跟连续有关的,但是球员连续得分的难…...

Python酷库之旅-第三方库Pandas(216)
目录 一、用法精讲 1011、pandas.DatetimeIndex.tz属性 1011-1、语法 1011-2、参数 1011-3、功能 1011-4、返回值 1011-5、说明 1011-6、用法 1011-6-1、数据准备 1011-6-2、代码示例 1011-6-3、结果输出 1012、pandas.DatetimeIndex.freq属性 1012-1、语法 1012…...

论文解析:计算能力资源的可信共享:利益驱动的异构网络服务提供机制
目录 论文解析:计算能力资源的可信共享:利益驱动的异构网络服务提供机制 KM-SMA算法 KM-SMA算法通过不断更新节点的可行顶点标记值(也称为顶标),利用匈牙利方法(Hungarian method)来获取匹配结果。在获取匹配结果后,该算法还会判断该结果是否满足Pareto最优性,即在没…...
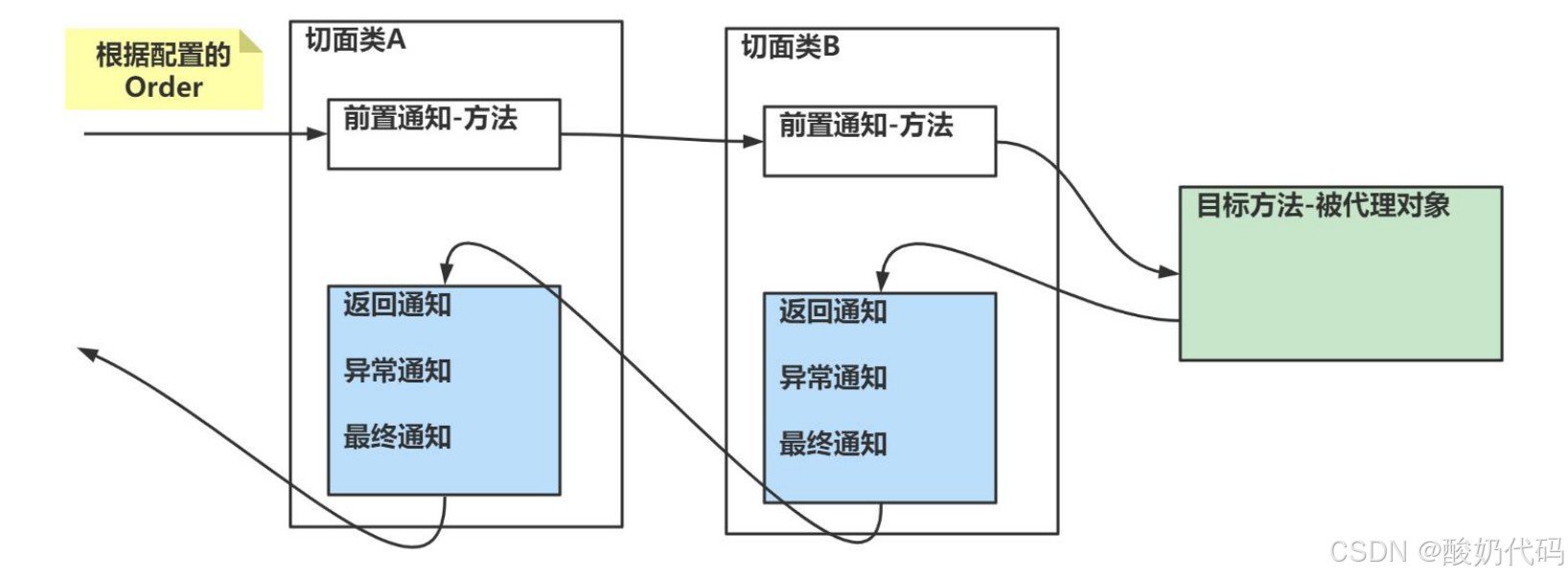
Spring AOP技术
1.AOP基本介绍 AOP 的全称 (aspect oriented programming) ,面向切面编程。 1.和传统的面向对象不同。 面向切面编程是根据自我的需求,将切面类的方法切入到其他的类的方法中。(这么说抽象吧!来张图来解释。) 如图 传…...
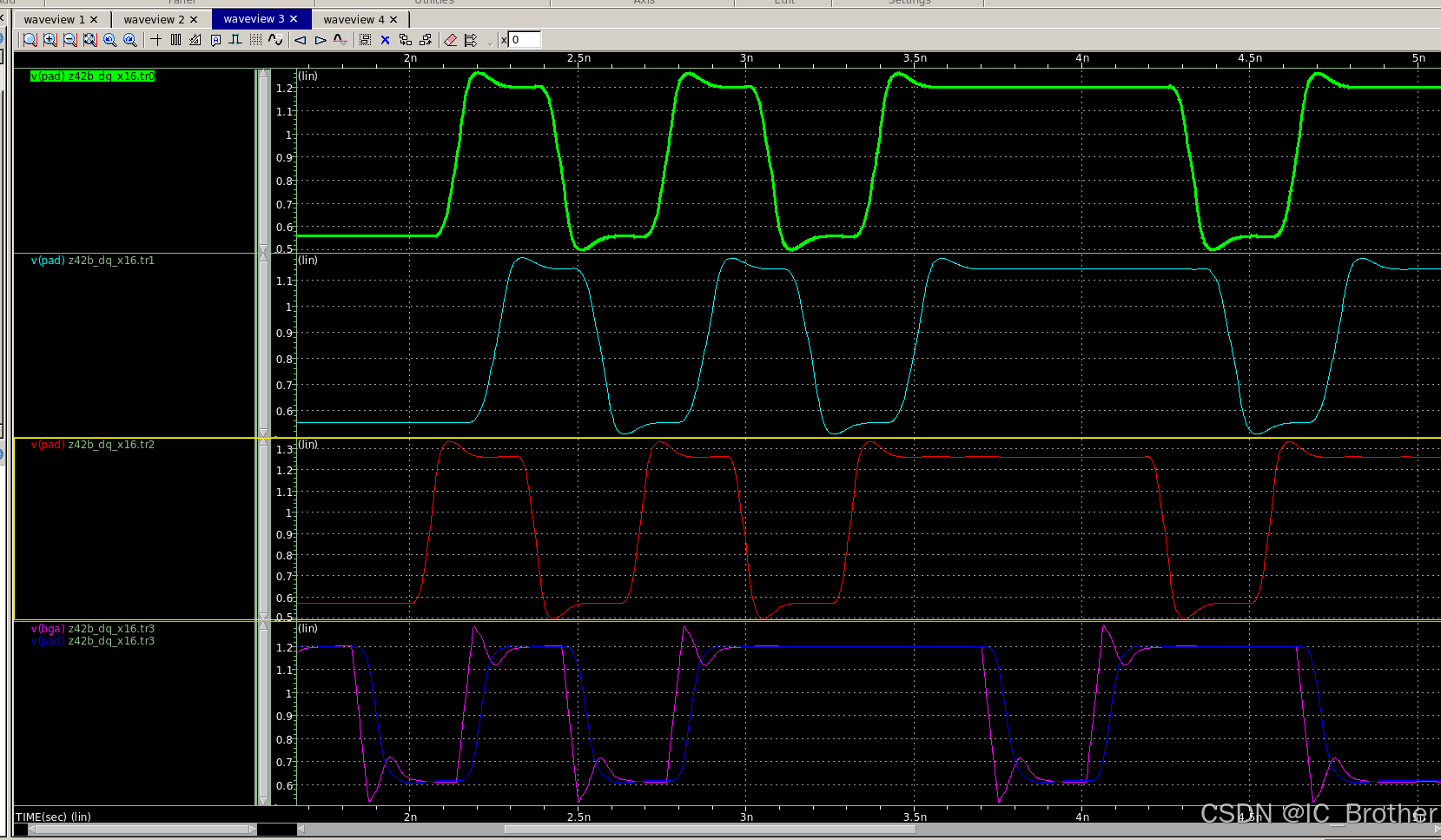
数字IC实践项目(10)—基于System Verilog的DDR4 Model/Tb 及基础Verification IP的设计与验证(付费项目)
数字IC实践项目(10)—基于System Verilog的DDR4 Model/Tb 及基础Verification IP的设计与验证(付费项目) 前言项目框图1)DDR4 Verification IP2)DDR4 JEDEC Model & Tb 项目文件1)DDR4 Veri…...

MATLAB保存多帧图形为视频格式
基本思路 在Matlab中,要将drawnow绘制的多帧数据保存为视频格式,首先需要创建一个视频写入对象。这个对象用于将每一帧图像数据按照视频格式的要求进行组合和编码。然后,在每次drawnow更新绘图后,将当前的图形窗口内容捕获为一帧图…...
 dict字典)
redis7.x源码分析:(3) dict字典
dict字典采用经典hash表数据结构实现,由键值对组成,类似于C中的unordered_map。两者在代码实现层面存在一些差异,比如gnustl的unordered_map分配的桶数组个数是(质数n),而dict分配的桶数组个数是࿰…...

连续九届EI稳定|江苏科技大学主办
【九届EI检索稳定|江苏科技大学主办 | IEEE出版 】 🎈【截稿倒计时】!!! ✨徐秘书:gsra_huang ✨往届均已检索,已上线IEEE官网 🎊第九届清洁能源与发电技术国际学术会议(CEPGT 2…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...
