二分搜索的三种方法
首先总的说一下二分搜索。如果区间具有二分性,这个二分性不仅仅是指区间是有序的,而是我们可以通过某一种性质将整个区间分成左区间和右区间。我们通过二分的方法去不断缩小查找的区间,最终让区间内没有元素,这个时候的我们就得到了分界的边界。
二分问题的难点在于边界的处理,整不好就死循环了,所以我们面对二分问题要一步一步分析,不要漏掉东西。
这里有两个原则大家要记住:
1)我们的最终目的就是让搜索区间没有一个元素;
2)left 的左面全都是<target的,right 的右面全都是>=target的(注意,这里的<,>=不是一定的,根据我们自己定的条件为主)。
这两个在这里不懂没关系,继续往下看就明白了。
一.全闭区间
即我们的查找区间的闭区间的,这个选择也影响到了我们的循环终止条件。我们的最终目的就是让区间没有一个元素,两面都是闭的,我们必须要 l<=r 。为什么?闭区间要想没有元素,要让 l 与 r 错开才行。
//闭区间
int n=nums.length;
int left=0;
int right=n-1;while(left<=right){int mid=left+(right-left)/2;if(nums[mid]<target){left=mid+1;}else{right=mid-1;}
}可能有的问题:
1.left和right的初始值为什么是这个?
left和right的初始值是根据我们区间的开闭写的。如果左面是开区间,left=-1,闭区间,left=0;右面同理,开区间,right=n,闭区间right=n-1。
2.那我们这么写的最终left和right分别指的下标是什么?
left 的左面全都是<target的,right 的右面全都是>=target的。所以说left指的是第一个>=target的元素,right指的是最后一个<target的元素。
3.为什么left要等于mid+1,为什么不能等于mid,right也是为什么不能等于mid?
还是刚刚的那句:left 的左面全都是<target的,right 的右面全都是>=target的。比如我们已经知道了 nums[mid]<target 了,所以说mid下标的元素一定<target,left的左面都是<target的,所以left直接等于mid+1就保证了left左面全都<target。right同理。
二.半闭半开
也是大家经常在网上看到的模板的类型,本人并不推荐这种写法,+1不+1的,可能在做什么模板题的时候觉得自我良好。但是二分是一种用于优化的算法,一般不会单独出现,在一些复杂的问题其实就很乱了。
上面是一些题外话,下面才是正题。
半闭半开有两种情况:左闭右开和左开右闭。
//左闭右开
int n=nums.length;
int left=0;
int right=n;while(left<right){int mid=left+(right-left)/2;if(nums[mid]<target){left=mid+1;}else{right=mid;}
}
//左开右闭
int n=nums.length;
int left=-1;
int right=n-1;while(left<right){int mid=left+(right-left+1)/2;if(nums[mid]<target){left=mid;}else{right=mid-1;}
}可能有的问题:
1.为什么上面left和right两次不同?
开的那一部分是取不到的,所以说我们就要多“往外”一点,因为一开始要全部元素都在搜索区间里。
2.为什么两种情况left和right这个+1那个-1的?
我们在上一种全闭的情况时提到:left 的左面全都是<target的,right 的右面全都是>=target的。这里就拿左闭右开举例。右面是开区间,也就是说right指向的下标的元素不在我们的搜索区间内,所以说已经满足了right 的右面全都是>=target的这个条件。我们此时说mid下标的这个元素>=target的,如果是闭区间,right要-1,但是根据开区间的性质,我们是取不到这个mid下标的元素的,可以理解成无形的减了一,我们就没必要再-1了,直接让right=mid就行了。但是left是闭的,所以要+1才能保证left 的左面全都是<target的。
左开右闭同理。
3.为什么在左开右闭时求mid要+1?
这个也是开区间影响的。在最后只剩下两个元素的时候,我们求mid,mid一定是指向左面的下标的,但是左面是开区间,也就是说左面的元素不在搜索区间内,不在区间怎么能判断呢?所以我们mid要+1。
4.结束时,left指向什么,right指向什么?
最终left和right会重合,所以这里说left或right都一样。
唉?为什么会重合?
因为这是一开一闭。我们最用要的是:left 的左面全都是<target的,right 的右面全都是>=target的。以左闭右开为例。比如说left和right重合的时候在t下标处,t下标对于的元素是>=target的(这是一定的),左区间是必的,所以left左面全都是<target的成立,右区间是开的,取不到t,所以right 的右面全都是>=target的。
明白上面的我们就知道left和right会指向第一个>=target的元素。
左开右闭的left和right会指向最后一个<target的元素。
5.如果区间内的元素全部<target或区间内元素全部>=target,那么left和right会指向什么?
在左必右开区间中,如果元素全部<target,我们会发现left和right会指向1,这肯定是不对的应该指向0才对。
在左开右闭,如果元素全部>=target,那么我们也会发现left和right指向错误。
这就是为什么不推荐这种写法,太乱了,我们不仅要关注加不加一,还要关注元素的问题。
三.全开区间
这是本人最推荐的一种方法,这种方法没有了+1-1的问题,方便记忆。
int n=nums.length;
int left=-1;
int right=n;while(left+1<right){int mid=left+(right-left)/2;if(nums[mid]>=target){right=mid;}else{left=mid;}
}简洁明了。
可能有的问题:
1.循环条件为什么是left+1<right?
还是那句话:我们的最终目的就是让搜索区间没有一个元素。其实当left+1=right的时候区间内就没有一个元素了对不对,所以说这个时候就要终止了。
2.left为什么不用+1,right为什么不用-1?
大家如果看懂上面关于这方面的解释的话这个自己就明白了。一句话:因为这是全开的。
3.结束时,left指向什么,right指向什么?
left指向最后一个<target的元素,right指向第一个>=target的元素。
如果区间内的元素全部<target,那left=-1,right=0;区间内元素全部>=target,那left=n-1,right=n。
四.总结
上面加粗的问题基本上可以涵盖大家可能问到的问题,如果还有问题可以在评论区讨论。还有,上的条件>=target或<target,这都不是固定的,根据真实情况进行修改,大家理解思想就行了。一定要着重理解上面反复提到的两个原则。
相关文章:

二分搜索的三种方法
首先总的说一下二分搜索。如果区间具有二分性,这个二分性不仅仅是指区间是有序的,而是我们可以通过某一种性质将整个区间分成左区间和右区间。我们通过二分的方法去不断缩小查找的区间,最终让区间内没有元素,这个时候的我们就得到…...

使用python编写工具:快速生成chrome插件相关文件结构
本文将详细分析一段用 wxPython 编写的 Python 应用程序代码。该程序允许用户创建一些特定文件并将它们保存在指定的文件夹中,同时也能够启动 Google Chrome 浏览器并打开扩展页面,自动执行一些操作。 C:\pythoncode\new\crxiterationtaburl.py 全部代码…...

内存、显存和GPU在Transformer架构中承担什么计算任务
目录 内存、显存和GPU在Transformer架构中承担什么计算任务 一、内存、显存和GPU的区别 二、在Transformer架构中的计算任务 内存、显存和GPU在Transformer架构中承担什么计算任务 是计算机系统中重要的组成部分,它们在Transformer架构中承担着不同的计算任务。以下是对这…...

【计算机网络】TCP协议特点3
心跳机制 什么是心跳机制 心跳机制是在计算机系统、网络通信和许多其他技术领域广泛应用的一种机制,用于检测两个实体之间的连接是否仍然活跃,或者设备是否还在正常运行。就是每隔一段时间发送一个固定的消息给服务端,服务端回复一个固定…...

移植LVGL8.2以及移植过程的理解
一、LVGL刷新显示(画点 OR 区域刷新颜色) 原来LCD的区域填充,由于没用到DMA就是普通的遍历区域块的坐标,需要传入的坐标就是显示区域的x轴起始与x轴尾部。y轴的起始与y轴的尾部。 怎么实现呢? SPI不加DMA实现区域填充…...

动态规划-背包问题——1049.最后一块石头的重量II
1.题目解析 题目来源 1049.最后一块石头的重量II——力扣 测试用例 2.算法原理 首先需要将该问题转化为0-1背包问题后再做分析 1.状态表示 根据数学中的知识我们知道将一个数字分为两个子数后求这两个子数的最小差值,那么就要求这两个子数尽可能接近于原数字的一…...
】并发性模式:如生产者-消费者、读写锁等。 架构模式:如MVC、MVVM等。属于23 种设计模式吗? RAII 的关系?)
【C++学习(37)】并发性模式:如生产者-消费者、读写锁等。 架构模式:如MVC、MVVM等。属于23 种设计模式吗? RAII 的关系?
并发性模式(如生产者-消费者、读写锁等)和架构模式(如 MVC、MVVM 等)并不属于 Gang of Four(GoF) 提出的 23 种经典设计模式 中。这些模式是其他领域中的设计模式,虽然它们和 GoF 的设计模式有交集,尤其是在程序架构和资源管理方面,但并不直接包含在 GoF 的 23 种设计…...

[Mysql] Mysql的多表查询----多表关系(下)
4、操作 方式二:创建表之后设置外键约束 外键约束也可以在修改表时添加,但是添加外键约束的前提是:从表中外键列中的数据必须与主表中主键列中的数据一致或者是没有数据。 语法: alter table <从表名> add constr…...

命名空间(namespace)详解(一)
域 在学习命名空间之前,我们首先要了解几种常见的域 一、域的种类 1、类作用域 类作用域是指定义在类内部的成员(包括数据成员和成员函数)的可见性和访问权限的范围 代码示例: #define _CRT_SECURE_NO_WARNINGS 1#include &…...

HarmonyOS ArkTs 解决流式传输编码问题
工作日志 日期:2024-11-15 标题:HarmonyOS ArkTs 解决流式传输编码问题 问题描述 问题:在处理流式数据的 HTTP 请求时,服务器返回的数据存在编码问题,导致数据无法正确地解码为字符串。部分数据在解码后出现了乱码…...

NPOI 实现Excel模板导出
记录一下使用NPOI实现定制的Excel导出模板,已下实现需求及主要逻辑 所需Json数据 对应参数 List<PurQuoteExportDataCrInput> listData [{"ItemName": "电缆VV3*162*10","Spec": "电缆VV3*162*10","Uom":…...

【OpenGL】OpenGL简介
文章目录 OpenGL概述OpenGL的本质OpenGL相关库核心库窗口管理glutfreeglutglfw 函数加载glewGLAD OpenGL概述 OpenGL(Open Graphics Library) 严格来说,本身并不是一个API,它是一个由Khronos组织制定并维护的规范(Specification)。OpenGL规范严格规定了…...

shell命令笔记
一、shell基本基础知识 1. shell命令中捕获上一个命令执行是否成功,通过判断 $? 是否为0,为0则表示成功,其他错误码则表示执行失败。 2. sheel命令中,变量赋值时默认都是字符串类型。赋值时须注意单引号与双引号的区别…...

qml显示OpenCV mat图片
文章目录 方式一QQuickPaintedItem 类介绍主要特点使用方法示例代码在 QML 中使用主要方法和属性注意事项编写OpenCV mat显示代码方式二本篇博客介绍在Qt6.5.3 qml项目里介绍如何显示OpenCV mat图片。视频:https://edu.csdn.net/learn/40003/654043?spm=3001.4143 在qml里显示…...

类与对象(2)---类的6个默认成员函数
1.类的6个默认成员函数 任何类在什么都不写时,编译器会自动生成以下6个默认成员函数。 默认成员函数:用户没有显式实现,编译器会生成的成员函数称为默认成员函数。 2.构造函数 2.1构造函数特性 构造函数的主要任务是初始化对象。 它有如下特…...

华为云租户网络-用的是隧道技术
1.验证租户网络是vxlan 2.验证用OVS 2.1控制节点VXLAN 本端ip(local ip)192.168.31.8 2.2计算节点VXLAN 本端ip(local ip)192.168.31.11 计算节点用的是bond0做隧道网络 2.3查看bond文件是否主备模式...

手搓神经网络(MLP)解决MNIST手写数字识别问题 | 数学推导+代码实现 | 仅用numpy,tensor和torch基本计算 | 含正反向传播数学推导
手写数字识别(神经网络入门) 文章目录 手写数字识别(神经网络入门)实验概述实验过程数据准备模型实现线性变换层前向传播反向传播更新参数整体实现 激活函数层(ReLU)前向传播反向传播整体实现 Softmax层&am…...

esp32c3安装micropython环境
esp32c3竟然支持micropython环境,真的太让人高兴了。主要是python开发比较友好,开发速度要快于C和C, 可以用来快速创意验证。 下载 首先到官网:MicroPython - Python for microcontrollers 点击“download”进入下载页面&#…...

ES6的Iterator 和 for...of 循环
写在前面 在JavaScript中,Iterator(遍历器)是一种接口,用于遍历数据结构(如数组、对象等)中的元素。它提供了一种统一的方式来访问集合中的每个项,包括值和位置。 默认 Iterator 接口 许多内…...

《C语言程序设计现代方法》note-4 基本类型 强制类型转换 类型定义
文章目录 助记提要7章 基本类型7.1 整数类型有符号整数和无符号整数整数类型的说明符整数类型的范围整型常量整数溢出读/写整数 7.2 浮点类型浮点数的范围浮点常量读/写浮点数 7.3 字符类型字符被当做整数来操作转义序列大小写转换scanf和printf读/写字符getchar和putchar读写字…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...
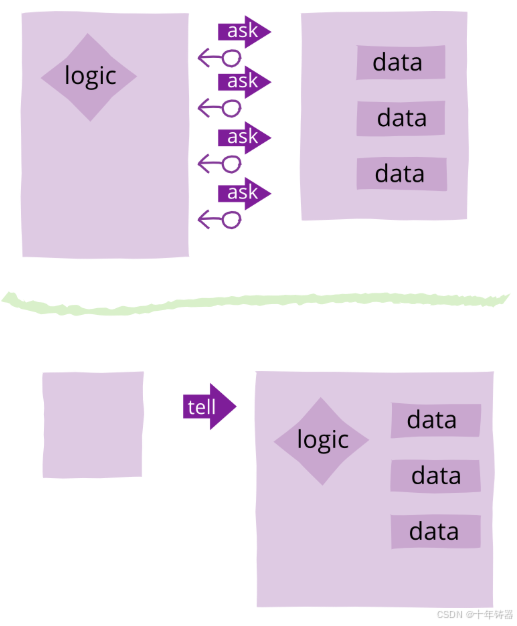
ABAP设计模式之---“Tell, Don’t Ask原则”
“Tell, Don’t Ask”是一种重要的面向对象编程设计原则,它强调的是对象之间如何有效地交流和协作。 1. 什么是 Tell, Don’t Ask 原则? 这个原则的核心思想是: “告诉一个对象该做什么,而不是询问一个对象的状态再对它作出决策。…...
