排序算法(基础)大全
一、排序算法的作用:
排序算法的主要作用是将一组数据按照特定的顺序进行排列,使得数据更加有序和有组织。
1. 查找效率:通过将数据进行排序,可以提高查找算法的效率。在有序的数据中,可以使用更加高效的查找算法,如二分查找、插值查找等,减少了查找的时间复杂度。
2. 统计分析:在排序过程中,可以对数据进行各种统计分析,如计算各种统计量、查找中位数、众数等。有序的数据更加便于进行统计分析和数据挖掘。
3. 数据压缩和编码:排序算法可以将数据重新排列,进而提供更好的数据压缩和编码方式,减少存储空间和传输带宽。
4. 数据归并和合并:在某些应用中,需要将多个有序的数据集合进行归并或合并,排序算法提供了这样的功能。例如,在合并两个有序的数组时,可以使用归并排序算法。
5. 数据的可视化和展示:有序的数据更容易进行可视化展示,可以更加直观地表达数据的分布和关系。
6. 数据库和文件系统中的索引:数据库和文件系统中的索引结构通常需要对数据进行排序,以提高查询和检索的效率。
总之,排序算法能够对数据进行有序排列,提高数据的组织性和可读性,提高查找和统计等操作的效率,是计算机科学和实际应用中的基础算法之一。
二、基础排序算法:
(1)选择排序:
故名思义,选择排序算法就是有选择地进行排序。其算法思想是:
1、将数组分成【已排序区】和【待排序区】
2、每一轮从【待排序区】中选择一个最小的元素放到【已排序区】
3、直到【待排序区】没有元素为止其算法的时间复杂度无论好坏都为O(
)
稳定性:不稳定
其过程如图:
关键代码实现:
#define swap(a,b){\ //交换a,b__typeof(a) __c=(a);\ //将a赋值给__c,同时,__c的类型与a的类型一样(a)=(b);\ //将b赋值给a(b)=__c;\ //将__c赋值给b
}
void selection_sort(int *arr,int l,int n){ //选择排序for(int i=l;i<n-1;i++){ //从下标0开始int ind=i; //假设下标为ind的数组元素最小for(int j=i+1;j<n;j++){if(arr[ind]>arr[j])ind=j; //如果有比下标ind更小的,则更新下标ind}swap(arr[i],arr[ind]); //将两个元素交换}return;
}(2)插入排序:
故名思义,插入排序就是不断进行插入调整的排序。其算法思想是:
1、将数组分成【已排序区】和【待排序区】
2、将【待排序区】后面第一个元素,向前插入到【已排序区】并进行调整
3、直到【待排序区】没有元素为止
其算法的时间复杂度最好的情况下为O(n),最坏的情况下或平均情况下为O()
稳定性:稳定
其过程如图:
关键代码实现:
#define swap(a,b){\ //交换a,b__typeof(a) __c=(a);\(a)=(b);\(b)=__c;\
}
void insert_sort(int *arr,int b,int n){ //插入排序,b=0for(int i=b+1;i<n;i++){ //待排序区从1开始int j=i; //记录已排序区的最大下标while(j>b&&arr[j]<arr[j-1]){ //对新插入到已排序区的元素进行排序swap(arr[j],arr[j-1]);j-=1;}}return;
}(3)希尔排序:
希尔排序(Shell Sort)是插入排序的一种改进版本,也称为递减增量排序。它通过将原始数组分割成多个子序列,对每个子序列进行插入排序,然后逐步缩小子序列的范围,最终完成排序。
希尔排序的基本算法思想:
选择一个增量序列,通常选择n/2、n/4、n/8...,直到增量为1。
对每个增量进行插入排序,将间隔为增量的元素分为一组,对每组进行插入排序。
缩小增量,重复第2步的操作,直到增量为1,即进行最后一次插入排序。
其算法的时间复杂度最好的情况下是O(nlogn),最坏的情况下是O(
)
稳定性:不稳定
其过程如图:
关键代码实现:
#define swap(a,b){\ //交换a,b__typeof(a) __c=(a);\ //将__c的类型在编译时,转换为与a相同的类型并赋值(a)=(b);\ //赋值交换(b)=__c;\ //赋值交换
}
void insert_sort(int *arr,int b,int n,int step){ //插入排序,b为起始下标,n为最大下标int ind=b; //记录要开始进行插入排序的点for(int i=b+step;i<n;i+=step){ //每次对间隔为step的元素排序if(arr[i]<arr[ind])ind=i; //记录数组下标大而数据小的元素}while(ind>b){ swap(arr[ind],arr[ind-step]); //交换元素ind-=step; //每次对间隔为step的元素进行排序}for(int i=b+2*step;i<n;i+=step){int j=i;while(arr[j]<arr[j-step]){swap(arr[j],arr[j-step]);j-=step;}}return;
}
void shell_sort(int *arr,int b,int n){int k=2,bc=(n-b),step;do{step=bc/k==0?1:(bc/k);for(int i=b,I=b+step;i<I;i++){insert_sort(arr,i,n,step);}k*=2;}while(step!=1);return;
}(4)快速排序:
快速排序是通过选择一个基准元素,将数组分成两个子数组,一组小于基准元素,另一组大于基准元素。然后对两个子数组分别递归地进行快速排序,最终将整个数组排序。
快速排序的基本算法思想:
1. 选择一个基准元素,通常选择数组的第一个或最后一个元素。
2. 定义两个指针,一个指向数组的第一个元素,一个指向数组的最后一个元素。
3. 移动左指针,直到找到一个大于等于基准元素的元素。
4. 移动右指针,直到找到一个小于等于基准元素的元素。
5. 交换左指针和右指针所指向的元素。
6. 重复步骤3-5,直到左指针和右指针相遇。
7. 将基准元素与左指针所指向的元素互换位置。
8. 进行递归,对基准元素左边的子数组和右边的子数组进行快速排序。其算法的时间复杂度最好的情况为O(nlogn),最坏的情况为O(
)。
其稳定性:不稳定
其过程如图:
关键代码实现:
#define swap(a,b){\__typeof(a) __c=(a);\(a)=(b);\(b)=__c;\
}
void quick_sort(int *arr,int l,int r){if(r-l<=2){if(r-l<=1)return;if(arr[l]>arr[l+1])swap(arr[l],arr[l+1]);return;}int x=l,y=r-1,z=arr[l];while(x<y){while(x<y&&z<=arr[y])--y;if(x<y)arr[x++]=arr[y];while(x<y&&arr[x]<=z)++x;if(x<y)arr[y]=arr[x];}arr[x]=z;quick_sort(arr,l,x);quick_sort(arr,x+1,r);return;
}
int main(){(5)归并排序:
归并排序(Merge sort)是一种经典的排序算法,它采用分治法的思想将问题分解为更小的子问题,并且通过递归的方式解决这些子问题。然后将子问题的解合并起来,最终得到原问题的解。
归并排序的基本算法思想:
1. 每次将数组不断地二分为两个子数组,直到每个子数组只剩下一个元素。
2. 然后将两个子数组逐个合并起来,形成一个有序的新数组。3.合并的方式是比较两个子数组的第一个元素,将较小的元素放入新数组中,并移动指针,继续比较下一个元素。
4. 重复上述步骤,直到将所有的子数组都合并起来,得到最终的有序数组。归并排序的时间复杂度:最好的情况下:O(nlogn);最坏的情况下:O(nlogn)。
这是一种稳定的排序算法,适用于各种数据类型。但是归并排序需要额外的存储空间来存储临时数组,空间复杂度为O(n)。
其过程如图:
原数组:[5,4,2,7,1,6,8,3]
关键代码实现:
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<string.h>
#define SMALL 1000000
__attribute__((constructor))
void __init_Rand__(){srand(time(0));
}
bool check(int *arr,int l,int r){for(int i=l+1;i<r;i++){if(arr[i]<arr[i-1])return false;}return true;
}
#define swap(a,b){\__typeof(a) __c=(a);\(a)=(b);\(b)=__c;\
}
#define TEST(func,arr,n){\printf("TEST:%s",#func);\int *temp=(int *)malloc(sizeof(int)*n);\memcpy(temp,arr,sizeof(int)*n);\long long b=clock();\func(temp,0,n);\long long e=clock();\if(check(temp,0,n)){\printf("\tOK");\}else{\printf("\tNO");\}\printf("\t%lldms\n",(e-b)*1000/CLOCKS_PER_SEC);\free(temp);\
}
int *getRandData(int n){int *arr=(int *)malloc(sizeof(int)*n);for(int i=0;i<n;i++){arr[i]=rand()%100+1;}return arr;
}
int *buff; //额外存储空间
void merge_sort(int *arr,int l,int r){ r为数组长度,l为开始位置,初始为0if(r-l<=1)return; //如果只有一个元素,返回结果int mid=(l+r)/2; //每次都将数组二分merge_sort(arr,l,mid); //递归二分前半段的数组merge_sort(arr,mid,r); //递归二分后半段的数组int p1=l,p2=mid,k=0;//p1记录第一个数组元素下标,p2记录中间元素下标,k记录当前位置,便于排序while(p1<mid||p2<r){ //前半段数组范围、后半段数组范围if(p2==r||(p1<mid&&arr[p1]<=arr[p2])){ buff[k++]=arr[p1++];}else{buff[k++]=arr[p2++];}}for(int i=l;i<r;i++)arr[i]=buff[i-l];return;
}
int main(){int *arr=getRandData(SMALL);buff=(int *)malloc(sizeof(int)*SMALL);TEST(merge_sort,arr,SMALL);free(buff);return 0;
}(6)基数排序:
基数排序是一种非比较型的排序算法,它将数据按照位数进行分组,分别对每个位数进行排序,直到最高位数排序完毕。基数排序可以用于对非负整数进行排序。
基数排序的基本算法思想如下:
1. 将待排序的数据从最低位开始,按照个位数进行分组。
2. 对每个分组进行计数排序,将数据按照个位数的大小进行排序。
3. 将所有分组的数据按照排序结果进行合并。
4. 重复步骤1-3,按照十位数、百位数等依次进行排序,直到最高位数排序完毕。基数排序的时间复杂度:最好的情况下:O(k*n);最坏的情况下:O(k*n)。其中k是最大数的位数,n是待排序数据的个数。
基数排序的空间复杂度是O(n+k)。
基数排序的优点是稳定性好,适用于数据量较大且每个数位数较小的情况。然而,基数排序的缺点是需要占用大量的额外空间,且对于负数无法直接排序。
基数排序过程如图:
关键代码实现:
#include<stdio.h>
#include<stdlib.h>
#include<time.h>
#include<string.h>
#define K 65536
#define SMALL 1000000
__attribute__((constructor))
void __init_Rand__(){srand(time(0));
}
#define swap(a,b){\__typeof(a) __c=(a);\(a)=(b);\(b)=__c;\
}
bool check(int *arr,int l,int r){for(int i=l+1;i<r;i++){if(arr[i]<arr[i-1])return false;}return true;
}
#define TEST(func,arr,n){\printf("TEST:%s",#func);\int *temp=(int *)malloc(sizeof(int)*n);\memcpy(temp,arr,sizeof(int)*n);\long long b=clock();\func(temp,0,n);\long long e=clock();\if(check(temp,0,n)){\printf("\tOK");\}else{\printf("\tNO");\}\printf("\t%lldms\n",(e-b)*1000/CLOCKS_PER_SEC);\free(temp);\
}
int *getRandData(int n){int *arr=(int *)malloc(sizeof(int)*n);for(int i=0;i<n;i++){arr[i]=rand()%100+1;}return arr;
}
void radix_sort(int *arr,int l,int r){int *cnt=(int *)malloc(sizeof(int)*K);int *temp=(int *)malloc(sizeof(int)*r);memset(cnt,0,sizeof(int)*K);for(int i=0;i<r;i++)cnt[arr[i]%K]+=1;for(int i=1;i<K;i++)cnt[i]+=cnt[i-1];for(int i=r-1;i>=l;i--)temp[--cnt[arr[i]%K]]=arr[i];memcpy(arr,temp,sizeof(int)*r);memset(cnt,0,sizeof(int)*K);for(int i=0;i<r;i++)cnt[arr[i]/K]+=1;for(int i=1;i<K;i++)cnt[i]+=cnt[i-1];for(int i=r-1;i>=l;i--)temp[--cnt[arr[i]/K]]=arr[i];memcpy(arr,temp,sizeof(int)*r);free(temp);free(cnt);return;
}
int main(){int *arr=getRandData(SMALL);TEST(radix_sort,arr,SMALL);free(arr);return 0;
}文章到此结束!
相关文章:

排序算法(基础)大全
一、排序算法的作用: 排序算法的主要作用是将一组数据按照特定的顺序进行排列,使得数据更加有序和有组织。 1. 查找效率:通过将数据进行排序,可以提高查找算法的效率。在有序的数据中,可以使用更加高效的查找算法&…...

Pytest从入门到精通
一、pytest单元测试框架 (1)什么是单元测试框架 单元测试是指在软件开发当中,针对软件的最小单位(函数,方法)进行正确性的检查测试。 (2)单元测试框架 java : junit和testng python : unittest和pytest (3)单元测试框架主要做什么? 1.测试发现:从多个文件里面去找到我们测试…...

《C++ 实现生成多个弹窗程序》
《C 实现生成多个弹窗程序》 在 C 编程中,我们可以利用特定的系统函数来创建弹窗,实现向用户展示信息等功能。当需要生成多个弹窗时,我们可以通过循环结构等方式来达成这一目的。 一、所需头文件及函数介绍 在 Windows 操作系统环境下&#…...

react 中 useRef Hook 作用
useRef是一个非常实用的钩子函数 一、访问和操作 DOM 元素 1. 获取 DOM 元素引用 1.1 基本原理 通过 useRef 我们可以直接操作 DOM 元素 1.2 代码示例 import React, { useRef, useEffect } from "react";const InputFocusComponent () > {const inputRef …...

Scala-键盘输入(StdIn)-用法详解
Scala 在 Scala 中,进行 键盘输入 主要通过 scala.io.StdIn 包来实现。 StdIn 提供了几个方法,用于从用户的键盘输入中读取不同类型的数据,如字符串、整数、浮点数等。 常用的输入方法有 readLine()、readInt()、readDouble()、readShort(…...

力扣(LeetCode)283. 移动零(Java)
White graces:个人主页 🙉专栏推荐:Java入门知识🙉 🐹今日诗词:雾失楼台,月迷津渡🐹 ⛳️点赞 ☀️收藏⭐️关注💬卑微小博主🙏 ⛳️点赞 ☀️收藏⭐️关注💬卑微小博主…...

ESP32C3单片机使用笔记---烧录MicroPython
使用MicroPython在ESP32C3单片机上编程,首先需要将MicroPython运行环境烧录到ESP32C3的Flash中去,步骤如下: 1.下载esptool烧录工具,下载地址: https://github.com/espressif/esptool 直接使用git clone git clone…...

Matter1.4重磅来袭,智能家居进入“互联”新纪元
近日,连接标准联盟(CSA)正式宣布推出最新的Matter1.4标准版本,并更新了一系列“史诗级”的增强功能,旨在提升现有智能家居之间的互操作性与兼容性,为智能家居用户带来更流畅的使用体验。 华普微,…...

tdengine学习笔记
官方文档:用 Docker 快速体验 TDengine | TDengine 文档 | 涛思数据 整体架构 TDENGINE是分布式,高可靠,支持水平扩展的架构设计 TDengine分布式架构的逻辑结构图如下 一个完整的 TDengine 系统是运行在一到多个物理节点上的,包含…...

机器学习-36-对ML的思考之机器学习研究的初衷及科学研究的期望
文章目录 1 机器学习最初的样子1.1 知识工程诞生(专家系统)1.2 知识工程高潮期1.3 专家系统的瓶颈(知识获取)1.4 机器学习研究的初衷2 科学研究对机器学习的期望2.1 面向科学研究的机器学习轮廓2.2 机器学习及其应用研讨会2.3 智能信息处理系列研讨会2.4 机器学习对科学研究的重…...

Linux 进程信号的产生
目录 0.前言 1. 通过终端按键产生信号 1.1 CtrlC:发送 SIGINT 信号 1.2 Ctrl\:发送 SIGQUIT 信号 1.3 CtrlZ:发送 SIGTSTP 信号 2.调用系统命令向进程发信号 3.使用函数产生信号 3.1 kill 函数 3.2 raise 函数 3.3 abort 函数 4.由软件条件产…...

CentOS8 在MySQL8.0 实现半同步复制
#原理 MySQL默认是异步的,不要求必须全部同步到从节点才返回成功结果; 同步复制: 用户发请求到代理, 代理收到请求后写/更新数据库写入到二进制日志bin_log, 然后必须等数据发到所有的从节点, 从节点全部收到数据后, 主节点才返回给客户端的成功结果。 弊端: 客…...

数据分析——Python绘制实时的动态折线图
最近在做视觉应用开发,有个需求需要实时获取当前识别到的位姿点位是否有突变,从而确认是否是视觉算法的问题,发现Python的Matplotlib进行绘制比较方便。 目录 1.数据绘制2.绘制实时的动态折线图3.保存实时数据到CSV文件中 import matplotlib.…...

【Redis】Redis的一些应用场景及使用策略
应用的场景 Redis 是一个高性能的内存数据库,广泛用于各种应用场景,以下是一些常见的应用场景: 缓存:Redis 的高读写性能使其非常适合作为缓存层,存储频繁访问的数据以减少数据库负载和加快响应时间。例如,…...
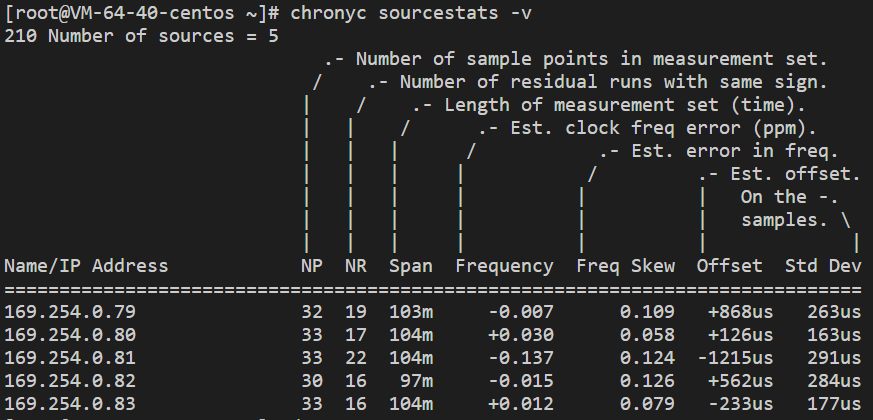
CentOS 8 安装 chronyd 服务
操作场景 目前原生 CentOS 8 不支持安装 ntp 服务,因此会发生时间不准的问题,需使用 chronyd 来调整时间服务。CentOS 8以及 TencentOS 3.1及以上版本的实例都使用 chronyd 服务实现时钟同步。本文介绍了如何在 CentOS 8 操作系统的腾讯云服务器上安装并…...

HarmonyOS ArkUI(基于ArkTS) 常用组件
一 Button 按钮 Button是按钮组件,通常用于响应用户的点击操作,可以加子组件 Button(我是button)Button(){Text(我是button)}type 按钮类型 Button有三种可选类型,分别为胶囊类型(Capsule)、圆形按钮(Circle…...
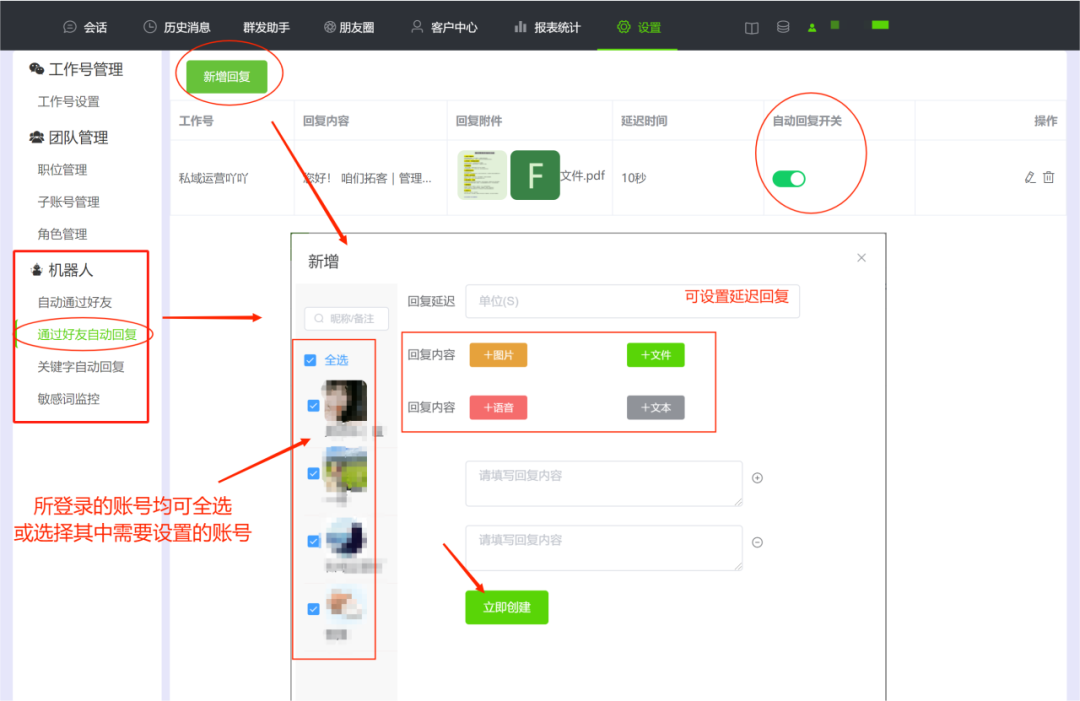
不用来回切换,一个界面管理多个微信
你是不是也有多个微信号需要管理? 是不是也觉得频繁切换账号很麻烦? 是不是也想提升多账号管理的效率? 在工作中,好的辅助工具,能让我们的效率加倍增长! 今天, 就给大家分享一个多微管理工具…...

MySQL系统优化
文章目录 MySQL系统优化第一章:引言第二章:MySQL服务架构优化1. 读写分离2. 水平分区与垂直分区3. 缓存策略 第三章:MySQL配置优化1. 内存分配优化Buffer Pool 的优化查询缓存与表缓存Key Buffer 2. 连接优化最大连接数会话超时连接池 3. 日志…...
:芋道的Docker容器化部署)
若依笔记(八):芋道的Docker容器化部署
目录 增加环境变量 DockerFile与镜像制作 nginx配置 vue3前端工程 首先搞个ECS阿里主机,1核4g足够,最大程度保证是docker运行来减少主机资源占用,同时因为是公有云,端口策略安全很重要,每个对外服务的端口要通过安全组放开; mysql的docker使用8版本,启动时候给my.cn…...

前端隐藏元素的方式有哪些?HTML 和 CSS 中隐藏元素的多种方法
当面试官突然问你:“前端隐藏元素的方式有哪些?”你还是只知道 display: none 吗? 其实,在前端开发的世界里,隐藏元素的方法非常多。每种方法都有自己的小技巧和使用场景,了解它们不仅能让你应对自如&…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

在树莓派上添加音频输入设备的几种方法
在树莓派上添加音频输入设备可以通过以下步骤完成,具体方法取决于设备类型(如USB麦克风、3.5mm接口麦克风或HDMI音频输入)。以下是详细指南: 1. 连接音频输入设备 USB麦克风/声卡:直接插入树莓派的USB接口。3.5mm麦克…...





