【2024 Optimal Control 16-745】【Lecture 2】integrators.ipynb功能分析
代码功能分析
导入库和项目设置
import Pkg; Pkg.activate(@__DIR__); Pkg.instantiate()
-
功能:激活当前文件夹为 Julia 项目环境,并安装当前项目中缺失的依赖包。
-
import Pkg:- 导入 Julia 的包管理模块
Pkg,用于管理项目依赖。
- 导入 Julia 的包管理模块
-
Pkg.activate(@__DIR__):- 激活当前脚本所在目录作为 Julia 项目环境。
@__DIR__是当前文件的目录路径。
- 激活当前脚本所在目录作为 Julia 项目环境。
-
Pkg.instantiate():- 根据项目的
Project.toml和Manifest.toml文件,安装所有依赖包。如果某些包未安装,这个命令会自动安装它们。
- 根据项目的
using LinearAlgebra
using PyPlot
using ForwardDiff
功能:加载必要的库:
-
using LinearAlgebra:- 导入线性代数模块,提供矩阵运算、特征值分解等功能。属于 Julia 标准库的一部分。
-
using PyPlot:- 导入
PyPlot模块,用于绘制图形。PyPlot是 Julia 对 Python Matplotlib 的接口,依赖于 Python 环境。
- 导入
-
using ForwardDiff:- 导入
ForwardDiff模块,提供自动微分功能,常用于数值优化和科学计算。
- 导入
定义摆动动力学函数
function pendulum_dynamics(x)l = 1.0g = 9.81θ = x[1] # 摆动角度 θθ̇ = x[2] # 摆动角速度 θ̇θ̈ = -(g / l) * sin(θ) # 根据摆动力学方程,计算角加速度 θ̈return [θ̇; θ̈] # 返回角速度和角加速度
end
- 功能:模拟单摆的动力学:
- 输入
x是状态向量[θ, θ̇],即当前角度和角速度。 - 计算结果是新的状态向量
[θ̇, θ̈],即角速度和角加速度。
- 输入
没有控制项时,动力学方程中的质量项m会相互抵消

通过拉格朗日方程推导,质量 m m m在动能和势能中对称出现,最终通过偏导数和求导操作被完全抵消。这反映了单摆在无外力(无控制项)情况下的动力学是一个与质量 m m m无关的系统,运动仅由摆长 l l l、重力加速度 g g g 和角度 θ \theta θ 决定。
θ 和 θ̇ 是 Julia 中的 Unicode 变量名,可以通过快捷输入实现。在代码中,这些符号只是普通变量名,它们的含义通过上下文和赋值来表达。
Forward Euler
定义前向欧拉法求解器
function pendulum_forward_euler(fun, x0, Tf, h)t = Array(range(0, Tf, step=h)) # 定义时间步长数组 tx_hist = zeros(length(x0), length(t)) # 创建状态记录数组,初始化为 0x_hist[:,1] .= x0 # 设置初始状态为 x0for k = 1:(length(t)-1)x_hist[:,k+1] .= x_hist[:,k] + h * fun(x_hist[:,k]) # 使用前向欧拉法计算下一步状态endreturn x_hist, t # 返回状态历史和时间步长
end
- 功能:
- 计算单摆运动的数值解,使用前向欧拉法。
fun是状态导数的计算函数(这里是pendulum_dynamics)。x0是初始状态[θ₀, θ̇₀]。Tf是模拟总时间。h是时间步长。- 返回:
x_hist:时间序列中摆的角度和角速度。t:时间序列。
.= 用于广播赋值,使得多个值可以逐元素地赋给目标数组或集合。
前向欧拉法-角度随时间的变化
x0 = [0.1; 0] # 初始角度为 0.1 弧度,初始角速度为 0
x_hist, t = pendulum_forward_euler(pendulum_dynamics, x0, 5, 0.1) # 运行模拟,总时间 5 秒,步长 0.1 秒plot(t, x_hist[1,:]) # 绘制角度随时间变化曲线
- 功能:
- 设置单摆的初始状态
- 使用
pendulum_forward_euler求解 5 秒内的摆动状态,步长为 0.1 秒。 - 绘制角度(
x_hist[1,:])随时间变化的曲线。
可视化图像
生成的图像展示了单摆在模拟时间内的角度随时间的变化,是一个振荡曲线(近似简谐振荡)。
由于采用的是前向欧拉法,随着时间步长的增加,数值解可能会出现一定的误差,尤其是在较长时间的模拟中。
-
数值方法的稳定性:
- 前向欧拉法是一种显式的数值积分方法,虽然实现简单,但在处理刚性方程或需要高精度的情况下可能不够稳定。可以考虑使用更高阶的方法,如四阶龙格-库塔法(RK4)。
-
时间步长的选择:
- 时间步长
h影响数值解的精度和稳定性。较小的步长通常提供更高的精度,但会增加计算量。需要根据具体问题权衡选择合适的步长。
- 时间步长
-
总模拟时间5s,时间步长0.1s
-
-
总模拟时间5s,时间步长0.01s
-

-
总模拟时间5s,时间步长0.01s

-
总模拟时间20s,时间步长0.01s

-
总模拟时间20s,时间步长0.001s

-
总模拟时间100s,时间步长0.001s

计算摆动系统离散化后的线性化矩阵 pendulum_euler_Ad
function pendulum_euler_Ad(x0, h)g = 9.81Ad = [1 h; -g*h*cos(x0[1]) 1]
end
功能解释:
-
function pendulum_euler_Ad(x0, h)- 定义了一个名为
pendulum_euler_Ad的函数,输入参数为:x0:当前状态向量(包括角度和角速度)。h:时间步长。
- 这个函数计算摆动系统离散化后的线性化矩阵。
- 定义了一个名为
-
g = 9.81- 定义重力加速度为 9.81 m/s²。
-
Ad = [1 h; -g*h*cos(x0[1]) 1]- 定义欧拉法计算的状态转移矩阵:
- 第一行表示角度更新(线性项)。
- 第二行表示角速度更新,包含重力和角度余弦的线性化影响。
- 定义欧拉法计算的状态转移矩阵:
调用函数并计算特征值
eigvals(pendulum_euler_Ad(0, 0.1))
功能解释:
-
pendulum_euler_Ad(0, 0.1)- 计算当初始角度 x 0 = 0 x_0 = 0 x0=0,时间步长 h = 0.1 h = 0.1 h=0.1 时的离散化矩阵。
-
eigvals()- 计算该矩阵的特征值,返回的结果为:
1.0 - 0.31320919526731655im 1.0 + 0.31320919526731655im - 表示系统状态转移矩阵的两个复数特征值。
- 计算该矩阵的特征值,返回的结果为:
等价于使用使用 ForwardDiff 自动求雅可比矩阵
using ForwardDiffh = 0.1 # 时间步长
Ad = I + h * ForwardDiff.jacobian(pendulum_dynamics, [0.0, 0.0]) # 计算A_d矩阵
eigvals(Ad) # 计算特征值

前向欧拉法-绘制特征值模与时间步长的关系图
eig_norm = zeros(100)
h = LinRange(0, 0.1, 100)
for k = 1:length(eig_norm)eig_norm[k] = max(norm.(eigvals(pendulum_euler_Ad([0;0], h[k]))))
end
plot(h, eig_norm)
功能解释:
-
eig_norm = zeros(100)- 初始化一个大小为 100 的数组,用于存储不同时间步长下特征值模的最大值。
-
h = LinRange(0, 0.1, 100)- 创建一个从 0 到 0.1 的线性空间,分为 100 等分,表示时间步长的变化范围。
-
for k = 1:length(eig_norm)- 开始循环,对每个时间步长计算对应的最大特征值模。
-
pendulum_euler_Ad([0;0], h[k])- 计算当前时间步长下的状态转移矩阵。
-
eigvals()- 计算当前矩阵的特征值。
-
norm.(eigvals(...))- 计算所有特征值的模。
-
max(...)- 获取当前时间步长下特征值模的最大值。
-
plot(h, eig_norm)- 绘制时间步长 h h h 和对应最大特征值模的关系图。
图像分析:
- 图像显示特征值模随时间步长 h h h 的变化:
- 当 h → 0 h \to 0 h→0 时,特征值模接近 1,系统趋于边际稳定。
- 随着 h h h 增大,特征值模逐渐超过 1,系统变得不稳定。

这段代码实现了摆动系统的离散化线性化分析,探索了时间步长对系统稳定性的影响,并通过绘制关系图验证了系统的边界稳定性条件。
四阶龙格-库塔方法(RK4)
实现四阶龙格-库塔方法(RK4)fd_pendulum_rk4
function fd_pendulum_rk4(xk, h)f1 = pendulum_dynamics(xk)f2 = pendulum_dynamics(xk + 0.5*h*f1)f3 = pendulum_dynamics(xk + 0.5*h*f2)f4 = pendulum_dynamics(xk + h*f3)return xk + (h/6.0)*(f1 + 2*f2 + 2*f3 + f4)
end
功能:
实现四阶龙格-库塔方法(RK4)的核心步骤:
f1到f4是四次不同点计算的斜率估计值。- 最终返回加权平均的更新状态,权重为 1 , 2 , 2 , 1 1, 2, 2, 1 1,2,2,1。
函数 pendulum_rk4
function pendulum_rk4(fun, x0, Tf, h)t = Array(range(0, Tf, step=h))x_hist = zeros(length(x0), length(t))x_hist[:,1] .= x0for k = 1:(length(t)-1)x_hist[:,k+1] .= fd_pendulum_rk4(x_hist[:,k], h)endreturn x_hist, t
end
功能:
用 RK4 模拟摆动系统。
x_hist用于存储状态历史,t是时间步数组。- 初始状态为
x0,逐步调用fd_pendulum_rk4更新状态。
RK4法模拟单摆系统角度随时间变化
x0 = [1.0; 0]
x_hist2, t_hist2 = pendulum_rk4(pendulum_dynamics, x0, 10, 0.1)
plot(t_hist2, x_hist2[1,:])
功能:
- 定义初始状态
x0 = [1.0; 0](初始角度为 1 弧度,初始角速度为 0)。 - 运行 RK4 模拟,总时长 10 秒,时间步长 0.1。
- 绘制角度随时间变化的曲线。

使用 ForwardDiff 计算雅可比矩阵
using ForwardDiff
Ad = ForwardDiff.jacobian(x -> fd_pendulum_rk4(x, 0.1), [0; 0])
norm.(eigvals(Ad))
功能:
-
using ForwardDiff:- 引入
ForwardDiff包,用于自动微分计算梯度、雅可比矩阵(Jacobian)和高阶导数。 - 在这里,它被用来计算一个函数的雅可比矩阵。
- 引入
-
ForwardDiff.jacobian(x -> fd_pendulum_rk4(x, 0.1), [0; 0]):-
雅可比矩阵的计算:
x -> fd_pendulum_rk4(x, 0.1)是一个匿名函数,它将输入 x x x 映射到通过四阶龙格-库塔方法(fd_pendulum_rk4)计算的状态更新结果。fd_pendulum_rk4是一个积分器函数,用于模拟系统的动力学行为。它的输入参数:- x x x 是当前状态向量(如 [角度; 角速度])。
0.1是时间步长 h h h。
- 雅可比矩阵是关于状态变量 x x x 的偏导数矩阵,其元素定义为:
J i j = ∂ f i ∂ x j J_{ij} = \frac{\partial f_i}{\partial x_j} Jij=∂xj∂fi
在这里, f i f_i fi 表示第 i i i 个方程的结果, x j x_j xj 表示第 j j j 个输入变量。

-
状态点
[0; 0]:- 指定初始状态为 x = [ 0 ; 0 ] x = [0; 0] x=[0;0],即摆的角度和角速度都为零。
-
输出
Ad:- 计算得到的雅可比矩阵 A d A_d Ad,表示在 x = [ 0 ; 0 ] x = [0; 0] x=[0;0] 处的局部线性化模型。
-
-
eigvals(Ad):- 计算矩阵 A d A_d Ad 的特征值:
- 特征值描述了状态变化的动态特性,决定系统的稳定性。
- 如果特征值的模(绝对值)小于 1,则系统是稳定的。
- 计算矩阵 A d A_d Ad 的特征值:
-
norm.(eigvals(Ad)):- 计算矩阵特征值的模(欧几里得范数)。
norm.是广播操作符(dot syntax),对特征值数组逐个计算模。- 输出是一个数组,其中每个值表示对应特征值的模。
总结
- 该代码通过自动微分计算四阶龙格-库塔方法在特定状态( x = [ 0 ; 0 ] x = [0; 0] x=[0;0])下的雅可比矩阵。
- 通过特征值的模,分析离散时间系统在该状态附近的稳定性。
- 如果所有特征值的模小于 1,系统在该状态下是局部稳定的。
RK4法特征值模随时间步长的变化
eig_norm = zeros(100)
h = LinRange(0, 1, 100)
for k = 1:length(eig_norm)eig_norm[k] = max(norm.(eigvals(ForwardDiff.jacobian(x -> fd_pendulum_rk4(x, h[k]), [0; 0]))))
end
plot(h, eig_norm)
功能:
- 初始化特征值模数组
eig_norm和时间步长范围h。 - 循环计算不同时间步长下特征值模的最大值。
- 绘制时间步长和特征值模的关系图,分析稳定性。

Backward Euler
反向欧拉法 pendulum_backward_euler
function pendulum_backward_euler(fun, x0, Tf, dt)t = Array(range(0, Tf, step=dt))x_hist = zeros(length(x0), length(t))x_hist[:,1] .= x0for k = 1:(length(t)-1)e = 1x_hist[:,k+1] .= x_hist[:,k]while e > 1e-8xn = x_hist[:,k] + dt.*fun(x_hist[:,k+1])e = norm(xn - x_hist[:,k+1])x_hist[:,k+1] .= xnendendreturn x_hist, t
end
该函数 pendulum_backward_euler 使用反向欧拉法Backward Euler Method模拟摆动系统的动力学行为。
工作原理总结
-
反向欧拉法:
- 隐式方法,在每个时间步需要迭代求解状态更新。
- 更加稳定,适合处理刚性系统。
-
迭代过程:
- 初始猜测下一步状态值。
- 利用当前猜测值计算下一步状态的动力学函数。
- 反复更新,直到误差小于设定的阈值。
函数头
function pendulum_backward_euler(fun, x0, Tf, dt)
fun: 表示系统的动力学函数,输入当前状态返回状态导数。例如,对于摆动系统,这个函数返回角速度和角加速度。x0: 初始状态向量,通常表示 [角度; 角速度]。Tf: 总模拟时间。dt: 时间步长。
时间数组与状态历史初始化
t = Array(range(0, Tf, step=dt))
x_hist = zeros(length(x0), length(t))
x_hist[:,1] .= x0
-
t:- 创建时间数组,从 0 到
Tf,以步长dt增加。 - 每个时间点对应系统的状态更新。
- 创建时间数组,从 0 到
-
x_hist:- 初始化一个矩阵,用于存储状态历史。行数为状态变量的数量(如角度和角速度),列数为时间点数量。
-
x_hist[:,1] .= x0:- 将第一列(即初始时间点)的状态设置为初始状态
x0。
- 将第一列(即初始时间点)的状态设置为初始状态
时间步循环
for k = 1:(length(t)-1)e = 1x_hist[:,k+1] .= x_hist[:,k]
- 遍历所有时间步,
k是当前时间步索引。 - 初始化误差
e = 1(用于收敛判断)。 - 用当前状态
x_hist[:,k]作为下一状态x_hist[:,k+1]的初始猜测值。
反向欧拉迭代
while e > 1e-8xn = x_hist[:,k] + dt.*fun(x_hist[:,k+1])e = norm(xn - x_hist[:,k+1])x_hist[:,k+1] .= xn
end
-
迭代公式:
- 反向欧拉法的核心方程:
x k + 1 = x k + h ⋅ f ( x k + 1 ) x_{k+1} = x_k + h \cdot f(x_{k+1}) xk+1=xk+h⋅f(xk+1) - 方程是隐式的,因为 x k + 1 x_{k+1} xk+1 既在左侧,也在右侧的动力学函数中。
- 反向欧拉法的核心方程:
-
计算新估计值
xn:- 使用当前估计值
x_hist[:,k+1]计算右侧的动力学值 f ( x k + 1 ) f(x_{k+1}) f(xk+1)。 - 更新 x k + 1 x_{k+1} xk+1 的新估计
xn。
- 使用当前估计值
-
误差计算
e:- 计算当前估计值
xn与之前的值x_hist[:,k+1]的欧几里得范数(即误差)。 - 如果误差小于 1 × 1 0 − 8 1 \times 10^{-8} 1×10−8,迭代停止,认为 x k + 1 x_{k+1} xk+1 已经收敛。
- 计算当前估计值
-
更新
x_hist[:,k+1]:- 将新的估计值
xn赋值给下一步状态x_hist[:,k+1]。
- 将新的估计值
返回结果
return x_hist, t
- 返回:
x_hist: 包含整个模拟过程中每个时间点的状态历史。t: 对应的时间点数组。
反向欧拉法-模拟角度随时间变化
x0 = [1.0; 0]
x_hist3, t_hist3 = pendulum_backward_euler(pendulum_dynamics, x0, 10, 0.001)
plot(t_hist3, x_hist3[1,:])
功能:
- 定义初始状态
x0 = [1.0; 0]。 - 用反向欧拉法模拟总时长 10 秒,时间步长为 0.001。
- 绘制角度随时间变化的曲线,展示系统动力学行为。

相关文章:

【2024 Optimal Control 16-745】【Lecture 2】integrators.ipynb功能分析
代码功能分析 导入库和项目设置 import Pkg; Pkg.activate(__DIR__); Pkg.instantiate()功能:激活当前文件夹为 Julia 项目环境,并安装当前项目中缺失的依赖包。 import Pkg: 导入 Julia 的包管理模块 Pkg,用于管理项目依赖。 …...

【linux】ubuntu下常用快捷键【笔记】
环境 硬件:通用PC 系统:Ubuntu 20.04 软件 : 打开终端窗口:Ctrl Alt T 关闭当前窗口:Alt F4 改变窗口大小:Alt F8 移动窗口: Alt F7 配合 “←”、“→”、“↑”、“↓”来移动窗口 …...

【Linux】常用命令练习
一、常用命令 1、在/hadoop目录下创建src和WebRoot两个文件夹 分别创建:mkdir -p /hadoop/src mkdir -p /hadoop/WebRoot 同时创建:mkdir -p /hadoop/{src,WebRoot}2、进入到/hadoop目录,在该目录下创建.classpath和README文件 分别创建&am…...

力扣-Hot100-数组【算法学习day.37】
前言 ###我做这类文档一个重要的目的还是给正在学习的大家提供方向(例如想要掌握基础用法,该刷哪些题?)我的解析也不会做的非常详细,只会提供思路和一些关键点,力扣上的大佬们的题解质量是非常非常高滴&am…...
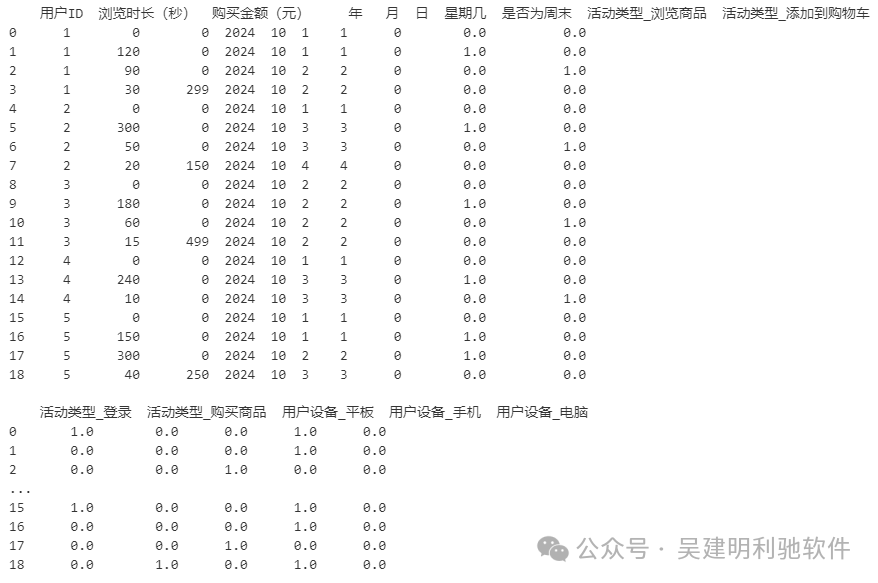
表格不同类型的数据如何向量化?
在进行机器学习项目时,首先需要获取数据,这些数据可以来自数据库、API、网络抓取,或从CSV、Excel等文件中读取。数据可能包含数值、文本和类别等多种特征,但原始数据通常无法直接用于训练模型。 数据预处理包括清洗、填补缺失值和…...

成都栩熙酷,电商服务新选择
在当今数字经济蓬勃发展的时代,电商平台已成为推动商业创新、促进消费升级的重要力量。抖音小店,作为短视频与电商深度融合的产物,凭借其独特的社交属性和内容营销优势,迅速吸引了大量用户和商家的关注。在这场变革中,…...

【java基础】微服务篇
参考黑马八股视频。 目录 Spring Cloud 5大组件 注册中心 负载均衡 限流 CAP和BASE 分布式事务解决方案 分布式服务的接口幂等性 分布式任务调度 Spring Cloud 5大组件 注册中心 Eureka的作用 健康监控 负载均衡 限流 漏桶固定速率,令牌桶不限速 CAP和BA…...

【LLM训练系列02】如何找到一个大模型Lora的target_modules
方法1:观察attention中的线性层 import numpy as np import pandas as pd from peft import PeftModel import torch import torch.nn.functional as F from torch import Tensor from transformers import AutoTokenizer, AutoModel, BitsAndBytesConfig from typ…...
uni-app快速入门(八)--常用内置组件(上)
uni-app提供了一套基础组件,类似HTML里的标签元素,不推荐在uni-app中使用使用div等HTML标签。在uni-app中,对应<div>的标签是view,对应<span>的是text,对应<a>的是navigator,常用uni-app…...

基于Amazon Bedrock:一站式多模态数据处理新体验
目录 引言 关于Amazon Bedrock 基础模型体验 1、进入环境 2、发现模型及快速体验 3、打开 Amazon Bedrock 控制台 4、通过 Playgrounds 体验模型 (1)文本生成 (2)图片生成 关于资源清理 结束语 引言 在云计算和人工智能…...
)
FAX动作文件优化脚本(MAX清理多余关键帧插件)
大较好,为大家介绍一个节省FBX容量的插件!只保留有用的动画轴向,其他不参与动画运动的清除! 一.插件目的:: 1.我们使用的U3D引擎产生的游戏资源包容量太大,故全方位优化动画资源; 2.在max曲线编辑器内,点取轴向太过麻烦,费事,直观清除帧大大提高效率。 如: 二:…...

Chapter 2 - 16. Understanding Congestion in Fibre Channel Fabrics
Transforming an I/O Operation to FC frames A read or write I/O operation (Figure 2-28) between an initiator and a target undergoes a series of transformations before being transmitted on a Fibre Channel link. 启动程序和目标程序之间的读取或写入 I/O 操作(图…...
pymysql、视图、触发器、存储过程、函数、流程控制、数据库连接池)
mysql数据库(六)pymysql、视图、触发器、存储过程、函数、流程控制、数据库连接池
pymysql、视图、触发器、存储过程、函数、流程控制、数据库连接池 文章目录 pymysql、视图、触发器、存储过程、函数、流程控制、数据库连接池一、pymysql二、视图三、触发器四、存储过程五、函数六、流程控制七、数据库连接池 一、pymysql 可以使用pip install pymysql安装py…...

RFdiffusion EuclideanDiffuser类解读
EuclideanDiffuser 是 RFdiffusion 中的一个关键类,专门设计用于对**三维空间中的点(如蛋白质的原子坐标)**进行扩散处理。它通过逐步向这些点添加噪音来实现扩散过程,从而为扩散模型提供输入数据,并通过逆扩散还原这些数据。 get_beta_schedule函数源代码 def get_beta…...

Flutter实现气泡提示框学习
前置知识点学习 GlobalKey GlobalKey 是 Flutter 中一个非常重要的概念,它用于唯一标识 widget 树中的特定 widget,并提供对该 widget 的访问。这在需要跨越 widget 树边界进行交互或在 widget 树重建时保持状态时尤其有用。 GlobalKey 的作用 唯一标…...

vue3 路由守卫
在Vue 3中,路由守卫是一种控制和管理路由跳转的机制。它允许你在执行导航前后进行一些逻辑处理,比如权限验证、数据预取等,从而增强应用的安全性和效率。路由守卫分为几种不同的类型,每种类型的守卫都有其特定的应用场景。 其实路…...
【MATLAB源码-第218期】基于matlab的北方苍鹰优化算法(NGO)无人机三维路径规划,输出做短路径图和适应度曲线.
操作环境: MATLAB 2022a 1、算法描述 北方苍鹰优化算法(Northern Goshawk Optimization,简称NGO)是一种新兴的智能优化算法,灵感来源于北方苍鹰的捕猎行为。北方苍鹰是一种敏捷且高效的猛禽,广泛分布于北…...

如何控制自己玩手机的时间?两台苹果手机帮助自律
对一些人来说,被智能手机“绑架”是一件心甘情愿的事,和它相处的一天中,不必面对现实的压力,它就像个“舒适区”。这是因为在使用手机的过程中,应用程序(尤其是游戏和社交媒体应用)会不断刺激大…...

【java-Neo4j 5开发入门篇】-最新Java开发Neo4j
系列文章目录 前言 上一篇文章讲解了Neo4j的基本使用,本篇文章对Java操作Neo4j进行入门级别的阐述,方便读者快速上手对Neo4j的开发。 一、开发环境与代码 1.docker 部署Neo4j #这里使用docker部署Neo4j,需要镜像加速的需要自行配置 docker run --name…...
简介和模块功能概览)
Python的3D可视化库 - vedo (1)简介和模块功能概览
文章目录 1. vedo和它支持的功能简介1.1 安装vedo1.2 命令行接口1.3 导出3D文件1.4 文件格式转换 2. vedo模块功能概览2.1 绘制和渲染visual 管理可视化、对象及其属性的显示的基类plotter 3D渲染colors 定义和显示颜色dolfin FEniCS/Dolfin库的支持 2.2 图形数据管理mesh 多边…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

计算机基础知识解析:从应用到架构的全面拆解
目录 前言 1、 计算机的应用领域:无处不在的数字助手 2、 计算机的进化史:从算盘到量子计算 3、计算机的分类:不止 “台式机和笔记本” 4、计算机的组件:硬件与软件的协同 4.1 硬件:五大核心部件 4.2 软件&#…...
