插值原理(数值计算方法)
插值原理(数值计算方法)
- 一. 原理介绍
- 二. 图例
- 三. 唯一性表述
一. 原理介绍
-
在数学中,
插值(Interpolation)是指通过已知的离散数据点,构造一个连续的函数,该函数能够精确地通过这些数据点,并用来估算在数据点之间或之外的值。 -
设 S = ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x n , y n ) S = {(x_1, y_1), (x_2, y_2), \dots, (x_n, y_n)} S=(x1,y1),(x2,y2),…,(xn,yn)是一组已知的离散数据点,其中插值问题的目标是找一个函数 f ( x ) f(x) f(x)使得:
f ( x i ) = y i ( i = 1 , 2 , … , n ) f(x_i) = y_i \quad( i = 1, 2, \dots, n) f(xi)=yi(i=1,2,…,n)
对所有的数据点都同时成立.
即函数f(x)必须通过所有给定的数据点。
二. 图例

例如我们有上述通过多项式插值方法得到的曲线图样:
(1)在插值点处,插值曲线和插值点的取值完全相同(或者说插值曲线完全经过所有数据点)
(2)在非插值点处没有任何参照指标,函数曲线的图样经过的点对于真实值可能存在较大偏差
(3)可以证明插值函数具有唯一性
这里解释一下插值函数的唯一性:
我们假设数据点有n+1个
- 插值函数的唯一性描述的是取其中一种具有相同表达形式的插值函数(例如
多项式插值),关于这个多项式插值的不同次项系数是可以唯一确定的。常见的我们取n次多项式来进行数据点的插值。 - 假设取高于数据点维数的多项式进行插值,我们可以证明其系数不唯一,例如取
n+1次多项式进行插值,等同于求解变量(n+2)大于方程数(n+1)的方程组,基于我们已知的数据点,所求解的方程存在无数组解。 - 如果取一
非线性函数对数据点进行插值,若存在n+1个待求解的系数(包含常数项),且系数之间相互独立,则该方程具有唯一解,也就是说对于n维的非线性插值函数也是唯一的。
我们说插值的函数是不唯一的,但当我们选定要插值的函数时,其待求解的系数和数据点数量等同时,插值函数是唯一的,由此我们说插值函数具有唯一性
三. 唯一性表述
这里给出其中一种关于n次多项式作为插值函数的唯一性的标准证明过程
- 问题表述
给定 n+1个插值点 ( x 0 , y 0 ) , ( x 1 , y 1 ) , … , ( x n , y n ) (x_0, y_0), (x_1, y_1), \ldots, (x_n, y_n) (x0,y0),(x1,y1),…,(xn,yn),希望找到一个次数不超过n的多项式
P ( x ) = a 0 + a 1 x + a 2 x 2 + ⋯ + a n x n P(x) = a_0 + a_1 x + a_2 x^2 + \cdots + a_n x^n P(x)=a0+a1x+a2x2+⋯+anxn
使得对每个插值点 ( x i , y i ) (x_i, y_i) (xi,yi),都有 P ( x i ) = y i P(x_i) = y_i P(xi)=yi
现证明其中参数 a 0 、 a 1 、 . . . 、 a n a_0、a_1、...、a_n a0、a1、...、an都可唯一确定。
- 建立方程组
(1)将插值点代入 P ( x ) P(x) P(x),可得方程组:
P ( x 0 ) = y 0 ⇒ a 0 + a 1 x 0 + a 2 x 0 2 + ⋯ + a n x 0 n = y 0 , P ( x 1 ) = y 1 ⇒ a 0 + a 1 x 1 + a 2 x 1 2 + ⋯ + a n x 1 n = y 1 , ⋮ P ( x n ) = y n ⇒ a 0 + a 1 x n + a 2 x n 2 + ⋯ + a n x n n = y n . \begin{aligned} & P(x_0) = y_0 \quad \Rightarrow \quad a_0 + a_1 x_0 + a_2 x_0^2 + \cdots + a_n x_0^n = y_0, \\ & P(x_1) = y_1 \quad \Rightarrow \quad a_0 + a_1 x_1 + a_2 x_1^2 + \cdots + a_n x_1^n = y_1, \\ & \quad \vdots \\ & P(x_n) = y_n \quad \Rightarrow \quad a_0 + a_1 x_n + a_2 x_n^2 + \cdots + a_n x_n^n = y_n. \end{aligned} P(x0)=y0⇒a0+a1x0+a2x02+⋯+anx0n=y0,P(x1)=y1⇒a0+a1x1+a2x12+⋯+anx1n=y1,⋮P(xn)=yn⇒a0+a1xn+a2xn2+⋯+anxnn=yn.
(2)写成矩阵形式:
[ 1 x 0 x 0 2 ⋯ x 0 n 1 x 1 x 1 2 ⋯ x 1 n ⋮ ⋮ ⋮ ⋱ ⋮ 1 x n x n 2 ⋯ x n n ] [ a 0 a 1 a 2 ⋮ a n ] = [ y 0 y 1 y 2 ⋮ y n ] . \begin{bmatrix} 1 & x_0 & x_0^2 & \cdots & x_0^n \\ 1 & x_1 & x_1^2 & \cdots & x_1^n \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_n & x_n^2 & \cdots & x_n^n \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_n \end{bmatrix}= \begin{bmatrix} y_0 \\ y_1 \\ y_2 \\ \vdots \\ y_n \end{bmatrix}. 11⋮1x0x1⋮xnx02x12⋮xn2⋯⋯⋱⋯x0nx1n⋮xnn a0a1a2⋮an = y0y1y2⋮yn .
记系数矩阵为 V V V,即:
V = [ 1 x 0 x 0 2 ⋯ x 0 n 1 x 1 x 1 2 ⋯ x 1 n ⋮ ⋮ ⋮ ⋱ ⋮ 1 x n x n 2 ⋯ x n n ] . V = \begin{bmatrix} 1 & x_0 & x_0^2 & \cdots & x_0^n \\ 1 & x_1 & x_1^2 & \cdots & x_1^n \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_n & x_n^2 & \cdots & x_n^n \end{bmatrix}. V= 11⋮1x0x1⋮xnx02x12⋮xn2⋯⋯⋱⋯x0nx1n⋮xnn .
该矩阵即为我们熟知的 范德蒙德矩阵(Vandermonde Matrix)。
- 解的结构
该线性方程组有解的充分必要条件是系数矩阵行列式 ∣ V ∣ |V| ∣V∣ 不为零,即 d e t ( V ) ≠ 0 det(V) \neq 0 det(V)=0
范德蒙德矩阵的行列式表示为:
det ( V ) = ∏ 0 ≤ i < j ≤ n ( x j − x i ) , \det(V) = \prod_{0 \leq i < j \leq n} (x_j - x_i), det(V)=0≤i<j≤n∏(xj−xi),
即有:
- 若对任意两个 x i x_i xi互不相同,则 d e t ( V ) ≠ 0 det(V) \neq 0 det(V)=0,方程组有唯一解。
显然,插值点之间互不相同,相互独立⇒该方程组有唯一解(得证)。
希望能够帮到迷途之中的你,知识有限,如有学术错误请及时指正,感谢大家的阅读
(^^)/▽ ▽\(^^)
相关文章:

插值原理(数值计算方法)
插值原理(数值计算方法) 一. 原理介绍二. 图例三. 唯一性表述 一. 原理介绍 在数学中,插值(Interpolation)是指通过已知的离散数据点,构造一个连续的函数,该函数能够精确地通过这些数据点&#…...
【Pikachu】SSRF(Server-Side Request Forgery)服务器端请求伪造实战
尽人事以听天命 1.Server-Side Request Forgery服务器端请求伪造学习 SSRF(服务器端请求伪造)攻击的详细解析与防范 SSRF(Server-Side Request Forgery,服务器端请求伪造) 是一种安全漏洞,它允许攻击者通…...

IDEA怎么定位java类所用maven依赖版本及引用位置
在实际开发中,我们可能会遇到需要搞清楚代码所用依赖版本号及引用位置的场景,便于排查问题,怎么通过IDEA实现呢? 可以在IDEA中打开项目,右键点击maven的pom.xml文件,或者在maven窗口下选中项目,…...

Discuz论坛网站管理员的默认用户名admin怎么修改啊?
当我们在某个论坛注册账号后,处于某种原因想要修改用户名,该如何修改? Discuz论坛网站管理员处于安全性或某种原因想要修改默认用户名admin该如何修改?驰网飞飞和你分享 其实非常简单,但是普通用户没有修改权限&…...

BIO、NIO、AIO的区别?
文章目录 BIO、NIO、AIO的区别?为什么不使用java 原生nio哪些项目使用了netty BIO阻塞I/O存在问题 NIO(nonblocking IO)Java NIO channel(通道)、buffer、selector(选择器) AIO(Asynchronous I/O) BIO、NIO…...
——FFmpeg源码中,读取出一个transport packet数据的实现)
音视频入门基础:MPEG2-TS专题(7)——FFmpeg源码中,读取出一个transport packet数据的实现
一、引言 从《音视频入门基础:MPEG2-TS专题(3)——TS Header简介》可以知道,TS格式有三种:分别为transport packet长度固定为188、192和204字节。而FFmpeg源码中是通过read_packet函数从一段MPEG2-TS传输流/TS文件中读…...

Flutter中sqflite的使用案例
目录 引言 安装sqflite 创建表 查询数据 添加数据 删除数据 更新数据 完整使用案例 引言 随着移动应用的发展,本地数据存储成为了一个不可或缺的功能。在Flutter中,sqflite 是一个非常流行且强大的SQLite插件,它允许开发者在移动设备…...

【2024 Optimal Control 16-745】【Lecture 2】integrators.ipynb功能分析
代码功能分析 导入库和项目设置 import Pkg; Pkg.activate(__DIR__); Pkg.instantiate()功能:激活当前文件夹为 Julia 项目环境,并安装当前项目中缺失的依赖包。 import Pkg: 导入 Julia 的包管理模块 Pkg,用于管理项目依赖。 …...

【linux】ubuntu下常用快捷键【笔记】
环境 硬件:通用PC 系统:Ubuntu 20.04 软件 : 打开终端窗口:Ctrl Alt T 关闭当前窗口:Alt F4 改变窗口大小:Alt F8 移动窗口: Alt F7 配合 “←”、“→”、“↑”、“↓”来移动窗口 …...

【Linux】常用命令练习
一、常用命令 1、在/hadoop目录下创建src和WebRoot两个文件夹 分别创建:mkdir -p /hadoop/src mkdir -p /hadoop/WebRoot 同时创建:mkdir -p /hadoop/{src,WebRoot}2、进入到/hadoop目录,在该目录下创建.classpath和README文件 分别创建&am…...

力扣-Hot100-数组【算法学习day.37】
前言 ###我做这类文档一个重要的目的还是给正在学习的大家提供方向(例如想要掌握基础用法,该刷哪些题?)我的解析也不会做的非常详细,只会提供思路和一些关键点,力扣上的大佬们的题解质量是非常非常高滴&am…...
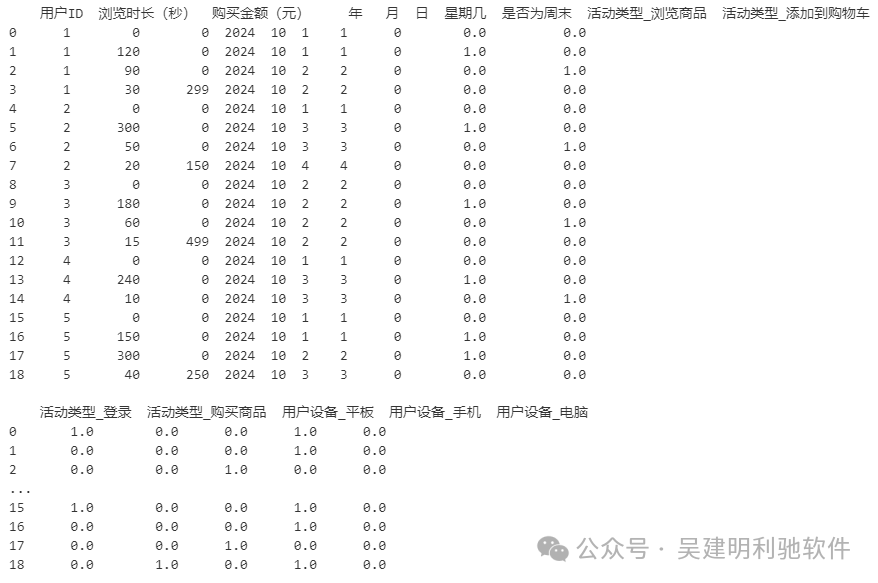
表格不同类型的数据如何向量化?
在进行机器学习项目时,首先需要获取数据,这些数据可以来自数据库、API、网络抓取,或从CSV、Excel等文件中读取。数据可能包含数值、文本和类别等多种特征,但原始数据通常无法直接用于训练模型。 数据预处理包括清洗、填补缺失值和…...

成都栩熙酷,电商服务新选择
在当今数字经济蓬勃发展的时代,电商平台已成为推动商业创新、促进消费升级的重要力量。抖音小店,作为短视频与电商深度融合的产物,凭借其独特的社交属性和内容营销优势,迅速吸引了大量用户和商家的关注。在这场变革中,…...

【java基础】微服务篇
参考黑马八股视频。 目录 Spring Cloud 5大组件 注册中心 负载均衡 限流 CAP和BASE 分布式事务解决方案 分布式服务的接口幂等性 分布式任务调度 Spring Cloud 5大组件 注册中心 Eureka的作用 健康监控 负载均衡 限流 漏桶固定速率,令牌桶不限速 CAP和BA…...

【LLM训练系列02】如何找到一个大模型Lora的target_modules
方法1:观察attention中的线性层 import numpy as np import pandas as pd from peft import PeftModel import torch import torch.nn.functional as F from torch import Tensor from transformers import AutoTokenizer, AutoModel, BitsAndBytesConfig from typ…...
uni-app快速入门(八)--常用内置组件(上)
uni-app提供了一套基础组件,类似HTML里的标签元素,不推荐在uni-app中使用使用div等HTML标签。在uni-app中,对应<div>的标签是view,对应<span>的是text,对应<a>的是navigator,常用uni-app…...

基于Amazon Bedrock:一站式多模态数据处理新体验
目录 引言 关于Amazon Bedrock 基础模型体验 1、进入环境 2、发现模型及快速体验 3、打开 Amazon Bedrock 控制台 4、通过 Playgrounds 体验模型 (1)文本生成 (2)图片生成 关于资源清理 结束语 引言 在云计算和人工智能…...
)
FAX动作文件优化脚本(MAX清理多余关键帧插件)
大较好,为大家介绍一个节省FBX容量的插件!只保留有用的动画轴向,其他不参与动画运动的清除! 一.插件目的:: 1.我们使用的U3D引擎产生的游戏资源包容量太大,故全方位优化动画资源; 2.在max曲线编辑器内,点取轴向太过麻烦,费事,直观清除帧大大提高效率。 如: 二:…...

Chapter 2 - 16. Understanding Congestion in Fibre Channel Fabrics
Transforming an I/O Operation to FC frames A read or write I/O operation (Figure 2-28) between an initiator and a target undergoes a series of transformations before being transmitted on a Fibre Channel link. 启动程序和目标程序之间的读取或写入 I/O 操作(图…...
pymysql、视图、触发器、存储过程、函数、流程控制、数据库连接池)
mysql数据库(六)pymysql、视图、触发器、存储过程、函数、流程控制、数据库连接池
pymysql、视图、触发器、存储过程、函数、流程控制、数据库连接池 文章目录 pymysql、视图、触发器、存储过程、函数、流程控制、数据库连接池一、pymysql二、视图三、触发器四、存储过程五、函数六、流程控制七、数据库连接池 一、pymysql 可以使用pip install pymysql安装py…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...
