「Mac玩转仓颉内测版24」基础篇4 - 浮点类型详解
本篇将详细介绍 Cangjie 中的浮点类型,包括浮点数的表示方法、精度、舍入与溢出处理、科学计数法表示、字面量的进制表示、常用运算、类型转换及应用场景,帮助开发者掌握浮点数的使用方法。
关键词
- 浮点类型表示
- 精度与舍入
- 溢出与下溢
- 科学计数法
- 类型转换
- 字面量表示
一、浮点类型概述
在 Cangjie 中,浮点类型用于表示包含小数部分的数值,主要包括两种类型:
- 单精度浮点数(Float32):约 6-7 位有效数字,适用于内存占用较低的场景。
- 双精度浮点数(Float64):约 15-16 位有效数字,适用于对精度要求较高的场景。
建议:若没有特殊的内存限制,优先使用 Float64 以获得更高精度。
二、浮点数的表示范围与精度
浮点数的表示范围取决于其位数限制:
- 单精度浮点数(Float32):范围约为 ±3.4 × 10^38。
- 双精度浮点数(Float64):范围约为 ±1.8 × 10^308。
由于浮点数使用二进制存储,在高精度运算中可能会出现舍入误差。
三、浮点类型字面量的表示
Cangjie 中的浮点类型字面量支持两种进制表示方式:十进制和十六进制。
-
十进制表示:字面量至少需要包含整数或小数部分。当没有小数部分时,必须包含指数部分(以 e 或 E 为前缀,底数为 10)。
-
十六进制表示:字面量以 0x 或 0X 为前缀,指数部分以 p 或 P 表示(底数为 2),同样至少需要包含整数或小数部分。
示例:
let a: Float32 = 3.14 // 十进制
let b: Float32 = 2e3 // 科学计数法
let c: Float32 = 0x1.1p0 // 十六进制
let d: Float64 = 0x.2p4 // 十六进制
四、浮点数的科学计数法表示
在 Cangjie 中,浮点数可以通过科学计数法表示,适合表示较大或较小的数值。使用 e 或 E 表示指数部分,例如:1.23e4 表示 1.23 × 10^4。
示例:
let bigNum = 3.45e6 // 表示 3450000
let smallNum = 2.67e-4 // 表示 0.000267println("大数: ${bigNum}, 小数: ${smallNum}")
输出:
大数: 3450000.000000, 小数: 0.000267
五、浮点数的运算
浮点数支持基础的算术运算和数学函数(如平方根、绝对值等),但需注意运算过程中可能出现精度损失。
5.1 算术运算
浮点数的加、减、乘、除操作如下:
let a: Float64 = 10.5
let b: Float64 = 3.2let sum = a + b
let difference = a - b
let product = a * b
let quotient = a / b println("加法: ${sum}, 减法: ${difference}, 乘法: ${product}, 除法: ${quotient}")
输出:
加法: 13.700000, 减法: 7.300000, 乘法: 33.600000, 除法: 3.281250
六、浮点数的溢出与下溢
- 溢出:当浮点数超过最大表示范围时,Cangjie 会返回 inf。
- 下溢:当浮点数低于最小表示范围时,Cangjie 会返回 0.000000。
let overflow = 1e309 // 超出 Float64 范围
let underflow = 1e-324 // 小于 Float64 范围println("溢出: ${overflow}, 下溢: ${underflow}")
输出:
溢出: inf, 下溢: 0.000000
七、浮点类型的后缀表示
为明确浮点字面量的类型,可在字面量后添加特定后缀:
| 后缀 | 类型 |
|---|---|
| f16 | Float16 |
| f32 | Float32 |
| f64 | Float64 |
示例:
let a = 3.14f32 // a 的类型为 Float32
let b = 2e3f32 // b 的类型为 Float32
let c = 2.4e-1f64 // c 的类型为 Float64
let d = .123e2f64 // d 的类型为 Float64
八、浮点数的类型转换
浮点数与整数之间可以相互转换,但浮点转整数时会截断小数部分。
let floatNum: Float64 = 10.99
let intNum: Int32 = Int32(floatNum) // 转换后小数部分被截断println("浮点数: ${floatNum}, 转换后的整数: ${intNum}")
输出:
浮点数: 10.990000, 转换后的整数: 10
九、浮点数的应用场景
浮点数适用于科学计算、货币金额表示等场景。
9.1 科学计算
let radius = 5.5
let area = 3.14159 * radius * radiusprintln("圆的面积: ${area}")
输出:
圆的面积: 95.033097
9.2 精确计算
在价格计算中,可使用浮点数表示更精确的金额:
let pricePerItem: Float64 = 19.99
let quantity: Float64 = 3.0
let totalPrice = pricePerItem * quantityprintln("总价: ${totalPrice}")
输出:
总价: 59.970000
十、浮点类型支持的操作符
浮点类型支持以下操作符:
- 算术操作符:如 +、-、*、/ 等。
- 关系操作符:如 <、>、== 等。
- 赋值操作符:如 =。
- 复合赋值操作符:如 +=、-=。
注意:浮点类型不支持自增(++)和自减(–)操作符。
小结
本篇详细讲解了 Cangjie 浮点类型的表示范围、科学计数法表示、字面量的进制表示、基本运算、舍入控制及应用场景,帮助开发者熟练运用浮点数处理涉及小数的计算任务。
下篇预告
下一篇将解析 Cangjie 的 布尔类型,探讨布尔运算及其在条件判断中的应用,敬请关注 「Mac玩转仓颉内测版25」基础篇5 - 布尔类型详解!
上一篇:「Mac玩转仓颉内测版23」基础篇3 - 深入理解整数类型
下一篇:「Mac玩转仓颉内测版25」基础篇5 - 布尔类型详解
作者:SoraLuna
链接:https://www.nutpi.net/thread?topicId=206
來源:坚果派
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
相关文章:

「Mac玩转仓颉内测版24」基础篇4 - 浮点类型详解
本篇将详细介绍 Cangjie 中的浮点类型,包括浮点数的表示方法、精度、舍入与溢出处理、科学计数法表示、字面量的进制表示、常用运算、类型转换及应用场景,帮助开发者掌握浮点数的使用方法。 关键词 浮点类型表示精度与舍入溢出与下溢科学计数法类型转换…...

【UGUI】Unity 背包系统实现02:道具信息提示与显示
在游戏开发中,背包系统是一个常见的功能模块,用于管理玩家拾取的物品。本文将详细介绍如何在 Unity 中实现一个简单的背包系统,包括道具信息的提示和显示功能。我们将通过代码和场景搭建来逐步实现这一功能。 1. 功能需求清单 在实现背包系…...

掌握移动端性能测试利器:深入JMeter手机录制功能
引言 在当今移动互联网时代,应用程序的性能和用户体验至关重要。为了确保应用程序在不同设备和网络环境下都能稳定运行,性能测试成为了不可或缺的一环。Apache JMeter作为一款强大的开源性能测试工具,不仅支持传统的PC端性能测试,…...

springboot010大学生入学审核系统的设计与实现(源码+包运行+LW+技术指导)
项目描述 随着信息技术在管理上越来越深入而广泛的应用,管理信息系统的实施在技术上已逐步成熟。本站是一个B/S模式系统,采用Spring Boot框架,MYSQL数据库设计开发,充分保证系统的稳定性。系统具有界面清晰、操作简单,…...

Qt/C++离线地图的加载和交互/可以离线使用/百度和天地图离线/支持手机上运行
一、前言说明 在地图应用中,有很多时候是需要断网环境中离线使用的,一般会采用两种做法,一种是只下载好离线瓦片地图,然后根据不同的缩放和经纬度坐标绘制瓦片。这种方式优点是任何地图都支持,只需要拿到瓦片即可&…...

从繁琐到优雅:用 PyTorch Lightning 简化深度学习项目开发
从繁琐到优雅:用 PyTorch Lightning 简化深度学习项目开发 在深度学习开发中,尤其是使用 PyTorch 时,我们常常需要编写大量样板代码来管理训练循环、验证流程和模型保存等任务。PyTorch Lightning 作为 PyTorch 的高级封装库,帮助…...

UE5 第一人称射击项目学习(完结)
这个项目几乎完结了。 也算我上手的第一个纯蓝图小项目。 现在只剩下缝缝补补了。 之前把子弹设计为蓝图,这里要引入C的面向对象思想,建立成员函数。 首先双击打开子弹的蓝图 这边就可以构造成员函数 写一个print your name 在这里生成成员函数后&am…...

Banana Pi BPI-CanMV-K230D-Zero 采用嘉楠科技 K230D RISC-V芯片设计
概述 Banana Pi BPI-CanMV-K230D-Zero 采用嘉楠科技 K230D RISC-V芯片设计,探索 RISC-V Vector1.0 的前沿技术,选择嘉楠科技的 Canmv K230D Zero 开发板。这款创新的开发板是由嘉楠科技与香蕉派开源社区联合设计研发,搭载了先进的勘智 K230D 芯片。 K230…...

【vim】使用 gn 组合命令实现搜索选中功能
gn是Vim 7.4新增的一个操作(motion),作用是跳到并选中下一个搜索匹配项。 具体说,Vim里执行搜索后,执行n操作只会跳转到下一个匹配项,而不选中它。但是我们往往需要对匹配项执行一些修改操作,例…...

【Python刷题】广度优先搜索相关问题
题目描述 小A与小B 算法思路 小A一次移动一步,但有八个方向,小B一次移动两步,只有四个方向,要求小A和小B最早的相遇时间。用两个队列分别记录下小A和小B每一步可以走到的位置,通过一个简单的bfs就能找到这些位置并…...

竞赛思享会 | 2024年第十届数维杯国际数学建模挑战赛D题【代码+演示】
Hello,这里是Easy数模!以下idea仅供参考,无偿分享! 题目背景 本题旨在通过对中国特定城市的房产、人口、经济、服务设施等数据进行分析,评估其在应对人口老龄化、负增长趋势和极端气候事件中的韧性与可持续发展能力。…...
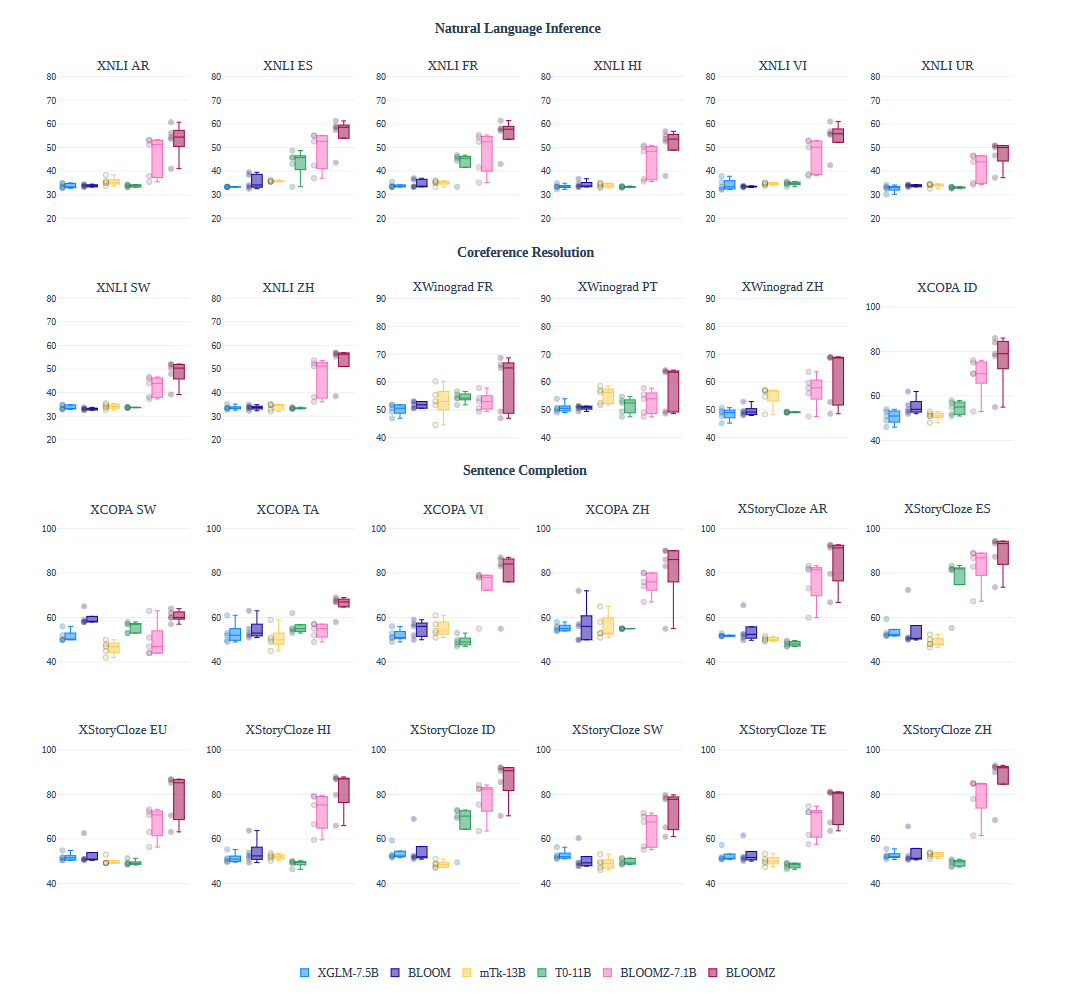
早期超大规模语言模型的尝试——BLOOM模型论文解读,附使用MindSpore和MindNLP的模型和实验复现
背景 预训练语言模型已经成为了现代自然语言处理pipeline中的基石,因为其在少量的标注数据上产生更好的结果。随着ELMo、ULMFiT、GPT和BERT的开发,使用预训练模型在下游任务上微调的范式被广泛使用。随后发现预训练语言模型在没有任何额外训练的情况下任…...

二分查找题目:有序数组中的单一元素
文章目录 题目标题和出处难度题目描述要求示例数据范围 解法一思路和算法代码复杂度分析 解法二思路和算法代码复杂度分析 题目 标题和出处 标题:有序数组中的单一元素 出处:540. 有序数组中的单一元素 难度 4 级 题目描述 要求 给定一个仅由整数…...

springboot基于Android的华蓥山旅游导航系统
摘 要 华蓥山旅游导航系统是一款专为华蓥山景区设计的智能导览应用,旨在为用户提供便捷的旅游信息服务。该系统通过整合华蓥山的地理信息、景点介绍、交通状况等数据,实现了对景区的全面覆盖。用户可以通过该系统获取实时的旅游资讯、交流论坛、地图等。…...

面向对象编程(OOP)深度解析:思想、原则与应用
🚀 作者 :“码上有前” 🚀 文章简介 :Java 🚀 欢迎小伙伴们 点赞👍、收藏⭐、留言💬 面向对象编程(OOP)深度解析:思想、原则与应用 一、面向对象编程的基本…...

iPhone 17 Air看点汇总:薄至6mm 刷新苹果轻薄纪录
我们姑且将这款iPhone 17序列的超薄SKU称为“iPhone 17 Air”,Jeff Pu在报告中提到,我同意最近关于 iPhone 17超薄机型采用6 毫米厚度超薄设计的传言。 如果这一测量结果被证明是准确的,那么将有几个值得注意的方面。 首先,iPhone…...

「OpenCV交叉编译」ubuntu to arm64
Ubuntu x86_64 交叉编译OpenCV 为 arm64OpenCV4.5.5、cmake version 3.16.3交叉编译器 gcc-arm-10.2-2020.11-x86_64-aarch64-none-linux-gnu 可在arm或linaro官网下载所需版本,本文的交叉编译器可点击链接跳转下载 Downloads | GNU-A Downloads – Arm Developer L…...
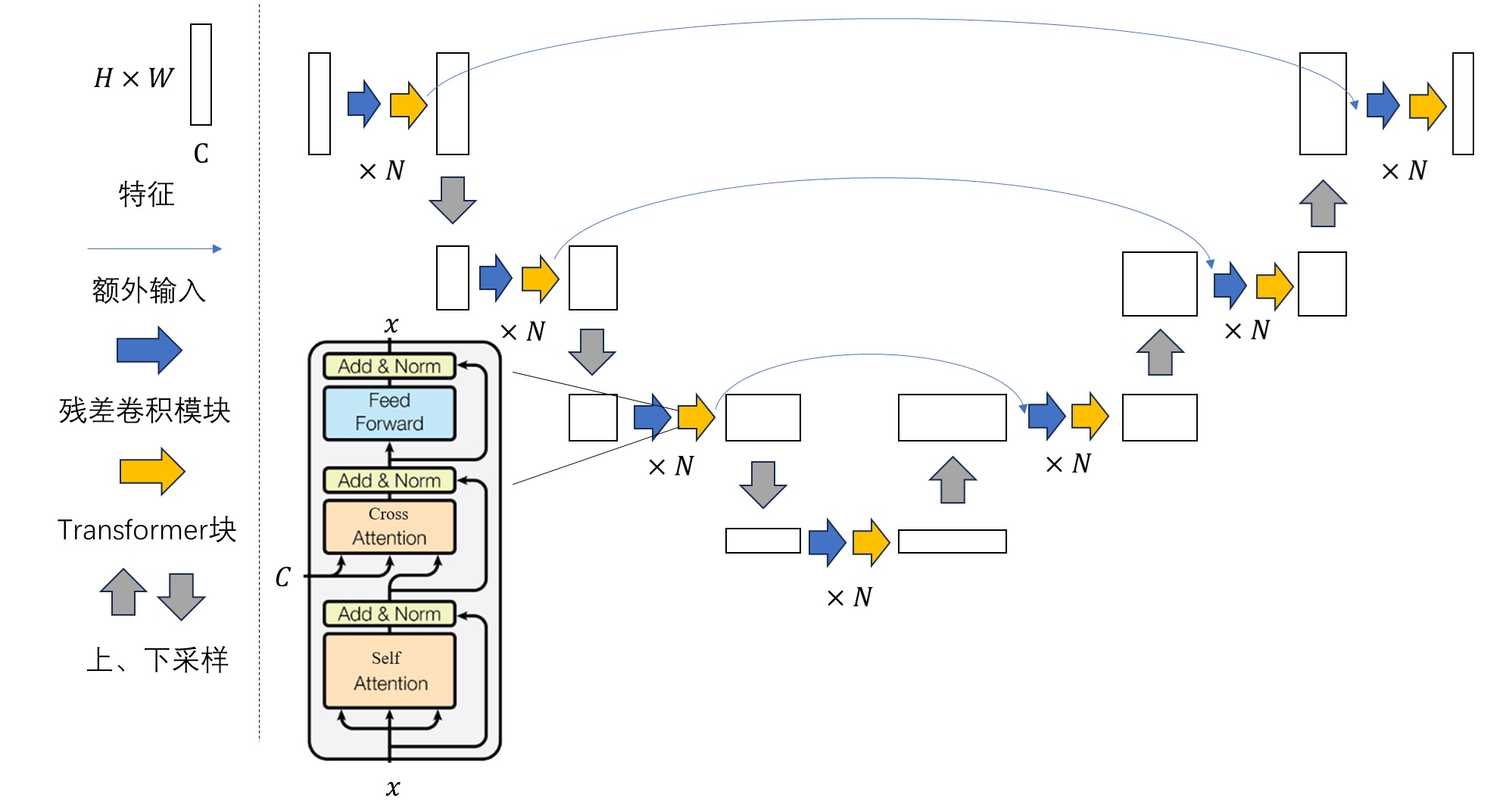
Stable Diffusion的解读(二)
Stable Diffusion的解读(二) 文章目录 Stable Diffusion的解读(二)摘要Abstract一、机器学习部分1. 算法梳理1.1 LDM采样算法1.2 U-Net结构组成 2. Stable Diffusion 官方 GitHub 仓库2.1 安装2.2 主函数2.3 DDIM采样器2.4 Unet 3…...

amd显卡和nVidia显卡哪个好 amd和英伟达的区别介绍
AMD和英伟达是目前市场上最主要的两大显卡品牌,它们各有自己的特点和优势,也有不同的适用场景和用户群体。那么,AMD显卡和英伟达显卡到底哪个好?它们之间有什么区别?我们又该如何选择呢?本文将从以下几个方…...

软件测试—— Selenium 常用函数(一)
前一篇文章:软件测试 —— 自动化基础-CSDN博客 目录 前言 一、窗口 1.屏幕截图 2.切换窗口 3.窗口设置大小 4.关闭窗口 二、等待 1.等待意义 2.强制等待 3.隐式等待 4.显式等待 总结 前言 在前一篇文章中,我们介绍了自动化的一些基础知识&a…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...
