【数据结构】树——链式存储二叉树的基础
写在前面
书接上文:【数据结构】树——顺序存储二叉树
本篇笔记主要讲解链式存储二叉树的主要思想、如何访问每个结点、结点之间的关联、如何递归查找每个结点,为后续更高级的树形结构打下基础。不了解树的小伙伴可以查看上文
文章目录
- 写在前面
- 一、链式二叉树的定义
- 二、链式二叉树的遍历
- 2.1、前序、中序以及后序遍历
- 前序遍历的代码实现
- 中序遍历的代码实现
- 后序遍历的代码实现
- 三、链式二叉树的元素个数
- 代码实现
- 四、链式二叉树的高度
- 代码实现
- 五、二叉树第k层节点个数
- 代码实现
- 六、二叉树查找值为x的节点
- 代码实现
- 七、链式存储二叉树的OJ
- 7.1、单值二叉树
- 代码实现
- 八、二叉树的创建和销毁
- 代码实现
一、链式二叉树的定义
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址。(二叉树有二叉链和三叉链两种表示方式,本文主要讲解二叉链。二叉链一般指孩子表示法,三叉连指孩子双亲表示法,这两种方式是二叉树最常见的表示方式,虽然还有孩子兄弟表示法,该中表示方式本质也是二叉链)


链式存储的结构体:
// 二叉链
struct BinaryTreeNode
{struct BinTreeNode* _pLeft;// 指向当前节点左孩子struct BinTreeNode* _pRight; // 指向当前节点右孩子BTDataType _data; // 当前节点值域
};
// 三叉链
struct BinaryTreeNode
{struct BinTreeNode* _pParent; // 指向当前节点的双亲struct BinTreeNode* _pLeft;// 指向当前节点左孩子struct BinTreeNode* _pRight; // 指向当前节点右孩子BTDataType _data; // 当前节点值域
};
- 上面的结构体就成功创建出链式存储的二叉树
二、链式二叉树的遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。( 不才默认左子树先运行后再运行右子树,再每次遍历先都需要规定一下左右子树的先后顺序。)

按照规则,二叉树的遍历有:前序/中序/后序的递归结构遍历:
2.1、前序、中序以及后序遍历
前序、中序以及后序遍历的思想都是相同的,只是根节点访问的先后顺序不同,我们这里以前序遍历为例子
1. 前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
2. 中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
3. 后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
- 程序由上到下运行,应当先访问当前值,后访问左右结点。

输出下图中的二叉树使用前序遍历的结果(结果需要包含
NULL)

- 结果为:
1,2,3,NULL,NULL,NULL,4,5,NULL,NULL,6,NULL,NULL
我们画图分析,使用微元法把每一个结点都逻辑细分为一棵小树(根结点与左右结点),在开始根节点1时,对应的左结点2和右结点4。

- 之后先输出根结点的值
1 - 后访问左结点
使用微元法把2结点微元成一棵小树

- 之后先输出根结点的值
2,此时结果为:1,2。 - 后访问左结点
使用微元法循环上述操作

- 之后先输出根结点的值
3,此时结果为:1,2,3。 - 后访问左结点
此时3的左节点使用微元法循环上述操作后可得下图

- 之后先输出根结点的值
NULL,此时结果为:1,2,3,NULL。 - 之后因为结点为
NULL,所以结束访问,返回到结点3。
此时结点3中,已经完成完成了左结点的范围,写在就需要范围右结点了

我们依旧使用微元法细分结点3的右结点,可得下图

- 之后先输出根结点的值
NULL,此时结果为:1,2,3,NULL,NULL。 - 之后因为结点为
NULL,所以结束访问,返回到结点3。
此时结点3的所以结点已经完成遍历,返回到结点2中,结点2已经完成当前结点与左结点值的遍历,接下来进入右结点值遍历中

使用微元法循环上述操作,直到整棵树的值遍历一便即可得到结果:1,2,3,NULL,NULL,NULL,4,5,NULL,NULL,6,NULL,NULL
上面我们手搓的思想与递归简直一毛一样,那么我们在代码实现中,就可以使用递归来解决前序遍历。
根据我们手搓的画图,最终我们可以得出下图:

前序遍历的代码实现
递归的思想就是大事化小,对于递归方面有问题的小伙伴可以看不才写的递归笔记:【C语言】函数递归
代码实现:
void PreOrder(BTNode* root) {if (root == NULL) {printf("NULL ");return;}printf("%d ", root->val);PreOrder(root->left);PreOrder(root->right);
}
根据上面手搓推理的逻辑,继续使用微元法来创建递归实现前序遍历

在上图这颗微元树中
- 首先需要判断这个树是否是空树,判断是否空树就是判断这个结点是否为
NULL,如果结点是NULL就打印NULL并且返回。 - 判断这个结点不为空后,因为是前序遍历,这时候就先打印根结点的值
root->val。 - 打印完成后就访问左孩子结点,之后再访问右孩子结点,完成。
- 在判断是否空树的条件中,恰好判断了结点为空的情况,这样也完成了我们访问左孩子或右孩子遇到结点为
NULL需要返回的情况。
内存中的栈增情况:

中序遍历的代码实现
与前序遍历的实现逻辑一模一样,只是执行根结点值打印时机不同。
void InOrder(BTNode* root) {if (root == NULL) {printf("NULL ");return;}InOrder(root->left);printf("%d ", root->val);InOrder(root->right);
}
后序遍历的代码实现
与前序遍历的实现逻辑一模一样,只是执行根结点值打印时机不同。
void PostOrder(BTNode* root) {if (root == NULL) {printf("NULL ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->val);
}
三、链式二叉树的元素个数
求链式二叉树的元素个数,我们还是先使用微元法来手搓计算。

计算下面二叉树有多少个元素

我们使用微元法先拆分一颗小树来分析如何计算
首先根节点不为NULL说明该根结点是有效结点,但是在这个结点中不能得到左孩子与右孩子右多少个元素个数。让左右孩子返回它有多少个元素结点。这样在这个小树中,我们才能返回这棵树有多少个结点。
所以又需要进入左右孩子中,去判断它是否是有多少个结点(如下图)

此时,我们还是不知道左右孩子各有多少个结点,我们再进入到左右孩子中(如下图)。

此时,我们还是不知道左右孩子各有多少个结点,我们再进入到左右孩子中。此时3的左节点使用微元法循环上述操作后可得下图

这时结点为NULL,说明该结点不是有效结点,返回0。

此时3结点就得到了左孩子结点的值为0,这时就需要进入右孩子中,让右孩子返回元素个数
同理,右孩子还是空,返回0,此时3结点得知左右孩子节点个数。
在3节点中左孩子返回结果 + 右孩子返回结果 再加上自身是有效结点+1就得到该结点的元素个数,左右元素个数为0,3节点是有效节点,所以返回1

节点2中就得到了左节点的元素个数,此时在按照上面的逻辑得到右节点个数为0(如下图)
 在
在2节点中左元素个数为1,右元素个数为0,2节点是有效节点,所以返回2(如下图)
根据上面的逻辑,我们可以轻松算出1结点的右子树元素个树为3个。

此时1结点中左孩子返回结果为2 右孩子返回结果为3 再加上自身是有效结点+1就得到该结点的元素个数为:6。
虽然也是遍历求解,但是我们这里是让每个底层结点自己统计完成后,逐步向上层返回结点个数 。
代码实现
int BinaryTreeSize(BTNode* root) {if (root == NULL) {return 0;}return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}
- 如果是空结点就返回
0 - 使用
微元法让左右结点自己返回有多少结点,再加上自身结点就是该小树的元素个数
四、链式二叉树的高度
求链式二叉树的高度,还是使用微元法,逻辑与求个数相似。

手搓下面二叉树的高度

我们使用微元法先拆分一颗小树来分析如何计算
在上图小树中,我们知道根节点不是空结点,这时候需要判断我们需要判断左右结点哪个孩子的高度高,之后我们在最高的子结点高度加上根结点的高度(+1)即可得到这个小树的高度,我们直接微元到原二叉树左子树的最底层中(如下图)
在上图中,左右孩子的高度是0,但次结点时有效结点,所以返回结果是:0+1。(最高的子结点高度加上根结点),
此时上层结点2就接收到左结点的高度是1,易得右结点的高度是0。
之后最高的子结点高度(1)加上根结点的高度(1)返回2(如下图)

根据上述逻辑,我们易的。1结点的右孩子返回高度是2(如下图)

这时两个孩子的高度都为2,所以该二叉树的高度为:2 + 1 = 3。
代码实现
int TreeHeight(BTNode* root) {if (root == NULL) {return 0;}int leftHeight = TreeHeight(root->left);int rightHeight = TreeHeight(root->right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}- 在递归中,返回的数据需要进行处理的返回值都必须进行保存,这样可以避免大量重复的递归。
- 每一次都需要保存左右结点的高度,这样就不需要多次重复递归即可判断出左孩子与右孩子哪个高度高。
五、二叉树第k层节点个数
同样使用微元法求出第K层中的节点个数。

手搓下面二叉树中第3层的高度

首先,我们需要有一个变量i来记录我们当前所在的层次是否在所对于的K层中,我们使用微元法先拆分一颗小树来分析如何计算
每进入一层,i变量就--,直到i变量为1时,说明当前的层次是正确的。但此时i == 3,这时候就需要进入根节点的左右孩子中,让左右孩子告诉根节点i==1是有多少个节点

首先进入到左孩子中,此时i==2,还是没进入到对于的节点,再次进入左右孩子中,此时发现i==1,这时候左孩子为3是有效节点,返回1,右孩子NULL不是有效节点。
这时候节点2就需要把左右孩子返回的数据相加后返回。

同理可得出右子树返回结果为:2。

即的出第3层的元素个数为:3。
代码实现
int TreeKLeve(BTNode* root,int k) {if (root == NULL) {//节点为空时,返回0return 0;}if (k == 1) { //节点不为空且层次为1时,返回1return 1;}int lnum = TreeKLeve(root->left, k - 1);//记录左孩子在K层时有多少个节点int rnum = TreeKLeve(root->right, k - 1);//记录右孩子在K层时有多少个节点return lnum + rnum;//返回左孩子在K层中节点 + 右孩子在K层中节点。即为当前根下K层中所有节点个数
}
- 在递归中,返回的数据需要进行处理的返回值都必须进行保存,这样可以避免大量重复的递归。
六、二叉树查找值为x的节点
相对简单,但是代码逻辑中会有坑

在下面二叉树中,找到值为
5的节点,并且返回该节点

只需要遍历找到值为5的节点,之后返回即可,逻辑与求元素个数大差不差。
代码实现
BTNode* BinaryTreeFind(BTNode* root, BTDataType x) {if (root == NULL) {return NULL;}if (root->val == x) {return root;}BTNode* lren = BinaryTreeFind(root->left,x);if (lren)return lren;BTNode* rren = BinaryTreeFind(root->right,x);if (rren)return rren;return NULL;
}
- 代码实现逻辑不断的遍历往下走,直到为空返回空,或者找到对应的值返回该节点。
- 如果既不为空也不是相对应的值,则接着往左右孩子中寻找X值。
- 如果左右孩子中都没有找到所对应的X值,则返回空值。
- 若找到了所对应的X值。则返回对应的节点。因为递归是函数的栈增
return不能直接返回到函数调用的阶段,需要一步步返回。 - 为了确保每次返回都是所对应的节点,我们需要进行判断每次返回的节点是否为空。如果不为空,则返回所找到的节点。
- 一旦涉及到需要对递归值进行判断的,都需要进行储存。
如果不进行判断返回,则在下一次函数递归返回中就直接返回空。(错误案例)
BTNode* BinaryTreeFind(BTNode* root, BTDataType x) {if (root == NULL) {return NULL;}if (root->val == x) {return root;}return NULL;
}
七、链式存储二叉树的OJ
7.1、单值二叉树
如果二叉树每个节点都具有相同的值,那么该二叉树就是单值二叉树。
只有给定的树是单值二叉树时,才返回 true;否则返回 false。

输入:[1,1,1,1,1,null,1]
输出:true
本题不可使用遍历。这里我们使用微元法判断一下我们这么确认每个节点都是相同的

使用根节点val与左右孩子的val值分别比较,即可判断出这个节点是否与左右孩子的值相同。
但是我们也不知道左右孩子的全部节点是否相同,但是如果此时不满住条件我们直接可以判断为假,所以我们先对该节点的左右孩子进行判断。

左节点判断结果不为假,继续判断右结点

此时右结点也不为假,所以我们需要递归往下判断,左右孩子的节点是否为假。如此递归,当遇到节点为NULL时,返回true,则说明到叶子节点都不为假,一旦为假,直接返回。
代码实现
bool isUnivalTree(struct TreeNode* root) {if (root == NULL) { // 基本情况:如果当前节点为空,返回 true(空树被认为是单值树)return true;}// 检查左子节点是否存在且值不同if (root->left != NULL && root->val != root->left->val) {return false;}// 检查右子节点是否存在且值不同if (root->right != NULL && root->val != root->right->val) {return false;}// 递归检查左子树和右子树return isUnivalTree(root->left) && isUnivalTree(root->right);
}
相似的逻辑,我们试试下面的题目:
- 100. 相同的树
- 101. 对称二叉树
- 572. 另一棵树的子树
八、二叉树的创建和销毁
通过前序遍历的数组:
1,2,3,NULL,NULL,NULL,4,5,NULL,NULL,6,NULL,NULL。构建二叉树
首先,我们需要把前序遍历的数组还原为二叉树,还原过程:

由上图可知,前序遍历的数组的还原过程,在数组下标+1我们就进行左孩子的赋值,当左孩子赋值NULL后,程序就返回节点,之后进行右结点的赋值,当右节点也赋值完成后,返回节点地址。
代码实现
typedef char BTDataType;
typedef struct BinaryTreeNode
{struct BinTreeNode* left;// 指向当前节点左孩子struct BinTreeNode* right; // 指向当前节点右孩子BTDataType val; // 当前节点值域}BTNode;
//前序递归创建二叉树
BTNode* CreateTree(char* arr, int* pi) {if (arr[*pi] == '#') {(*pi)++;return NULL;}BTNode* node = (BTNode*)malloc(sizeof(BTNode));node->val = arr[(*pi)++];node->left = CreateTree(arr, pi);node->right = CreateTree(arr, pi);return node;
}void test2() {char arr[] = { '1','2','3','#','#','#','4','5','#','#','6','#','#' };//'#'代表NULLint i = 0;BTNode* node = CreateTree(arr, &i);
}
我们画部分的递归展开图以便理解:

以上就是本章所有内容。若有勘误请私信不才。万分感激💖💖 如果对大家有帮助的话,就请多多为我点赞收藏吧~~~💖💖

ps:表情包来自网络,侵删🌹
相关文章:

【数据结构】树——链式存储二叉树的基础
写在前面 书接上文:【数据结构】树——顺序存储二叉树 本篇笔记主要讲解链式存储二叉树的主要思想、如何访问每个结点、结点之间的关联、如何递归查找每个结点,为后续更高级的树形结构打下基础。不了解树的小伙伴可以查看上文 文章目录 写在前面 一、链…...

STM32-- keil常见报错与解决办法
调试问题 1. keil在线调试需要点击好几次运行才可以运行,要是直接下载程序直接就不运行。 解决:target里面的use microlib要勾选,因为使用了printf。 keil在线调试STM32,点三次运行才能跑到main的问题解决。 keil在线调试STM32…...
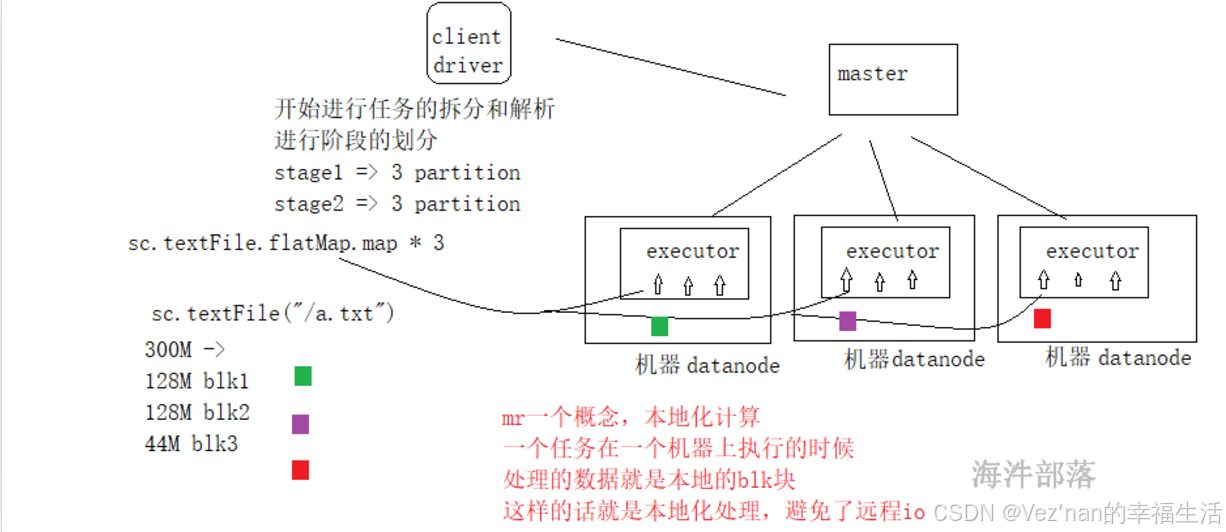
【大数据学习 | Spark-Core】RDD的概念与Spark任务的执行流程
1. RDD的设计背景 在实际应用中,存在许多迭代式计算,这些应用场景的共同之处是,不同计算阶段之间会重用中间结果,即一个阶段的输出结果会作为下一个阶段的输入。但是,目前的MapReduce框架都是把中间结果写入到HDFS中&…...

一文读懂埋阻埋容工艺
PCB 埋阻埋容工艺是一种在 PCB 板内部埋入电阻和电容的工艺。通常情况下, PCB 上电阻和电容都是通过贴片技术直接焊接在板面上的,而埋阻埋容工艺则将电 阻和电容嵌入到 PCB 板的内部层中,这种印制电路板,其自下而上依次包括第一介电 层,隐埋电…...
)
mysql 数据表导出为 markdown(附 go 语言 gorm 的实际使用)
前言 通常业务系统开发中,数据库的设计与维护是至关重要的环节。而数据库的文档化则是确保团队成员之间有效沟通、快速理解系统架构的基础。 但目前数据文档都是手动写的,耗时费力,由于当前项目使用的是 mysql 作为存储引擎,找找…...

本地云存储 MinIO 中修改用户密码
本地云存储 MinIO 中修改用户密码 MinIO 中修改用户密码前提条件步骤 1:安装 MinIO Client对于 Linux/macOS:对于 Windows: 步骤 2:配置 MinIO Client步骤 3:查看现有用户步骤 4:修改用户密码步骤 5&#x…...

go项目中比较好的实践方案
工作两年来,我并未遇到太大的挑战,也没有特别值得夸耀的项目。尽管如此,在日常的杂项工作中,我积累了不少心得,许多实践方法也在思考中逐渐得到优化。因此,我在这里记录下这些心得。 转发与封装 这个需求…...
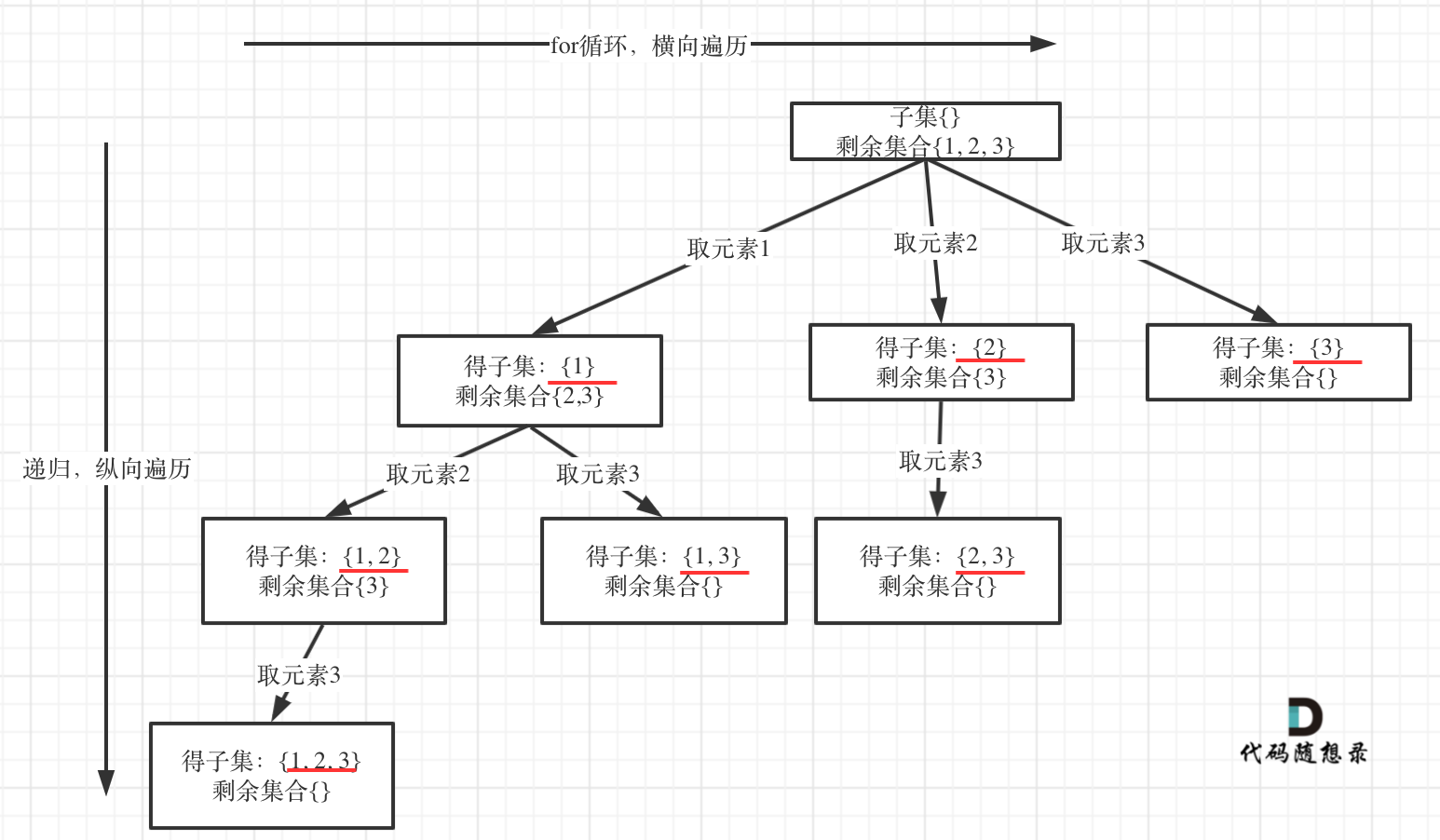
回溯法基础入门解析
回溯法 前 言 回溯法也可以叫做回溯搜索法,它是一种搜索的方式。回溯是递归的副产品,只要有递归就会有回溯。回溯法,一般可以解决如下几种问题: 组合问题:N个数里面按一定规则找出k个数的集合切割问题:一…...
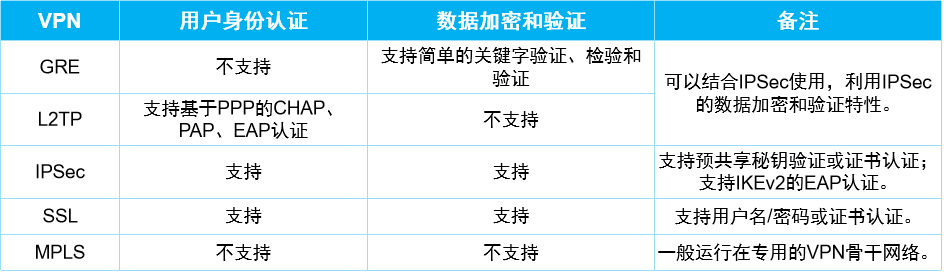
计算机网络-VPN虚拟专用网络概述
前面我们学习了在企业内部的二层交换机网络、三层路由网络包括静态路由、OSPF、IS-IS、NAT等,现在开始学习下VPN(Virtual Private Network,虚拟专用网络),其实VPN可能很多人听到第一反应就是梯子,但是其实这…...

信创时代的数据库之路:2024 Top10 国产数据库迁移与同步指南
数据库一直是企业数字化和创新的重要基础设施之一。从传统的关系型数据库到非关系型数据库、分析型数据库,再到云数据库和多模数据库,这一领域仍在持续变革中,各种新型数据库产品涌现,数据管理的能力和应用场景也由此得到了扩展。…...

自制游戏:监狱逃亡
第一个游戏,不喜勿喷: #include<bits/stdc.h> #include<windows.h> using namespace std; int xz; int ruond_1(int n){if(xz1){printf("撬开了,但站在你面前的是俄罗斯内务部特种部队的奥摩大帝,你被九把加特…...

小雪时节,阴盛阳衰,注意禁忌
宋张嵲《小雪作》 霜风一夜落寒林,莽苍云烟结岁阴。 把镜渐无勋业念,爱山唯驻隐沦心。 冰花散落衡门静,黄叶飘零一迳深。 世乱身穷无可奈,强将悲慨事微吟。 网络图片:小雪时节 笔者禁不住喟然而叹:“冰…...

CPU性能优化--微操作
x86 架构处理器吧复杂的CISC指令转为简单的RISC微操作。这样做最大的优势是微操作可以乱序执行,一条简单的相加指令--比如ADD,EAX, EBX,只产生一个微操作,而很多复杂指令--比如ADD, EAX 可能会产生两个微操作,一个将数…...

工厂模式
主要解决对象的创建问题 首先是简单工厂 只有一个工厂类,每次有新的产品就需要修改里面接口的内容,违反了封闭原则 //1、定义抽象产品类 class AbstractCar { public:AbstractCar() default;virtual ~AbstractCar() default;virtual void showName(…...

嵌入式系统与OpenCV
目录 一、OpenCV 简介 二、嵌入式 OpenCV 的安装方法 1. Ubuntu 系统下的安装 2. 嵌入式 ARM 系统中的安装 3. Windows10 和树莓派系统下的安装 三、嵌入式 OpenCV 的性能优化 1. 介绍嵌入式平台上对 OpenCV 进行优化的必要性。 2. 利用嵌入式开发工具,如优…...
编程之路,从0开始:动态内存笔试题分析
Hello大家好,很高兴我们又见面啦! 给生活添点passion,开始今天的编程之路。 今天我们来看几个经典的动态内存笔试题。 1、题目1 #define _CRT_SECURE_NO_WARNINGS #include<stdio.h> #include<string.h> void GetMemory(char* …...
物联网研究实训室建设方案
一、引言 随着物联网技术的快速发展,其在各个行业的应用越来越广泛,对物联网专业人才的需求也日益增加。为满足这一需求,建设一个符合现代化教学需求的物联网研究实训室,对于提高学生的实践能力和创新能力具有重要意义。本方案旨…...
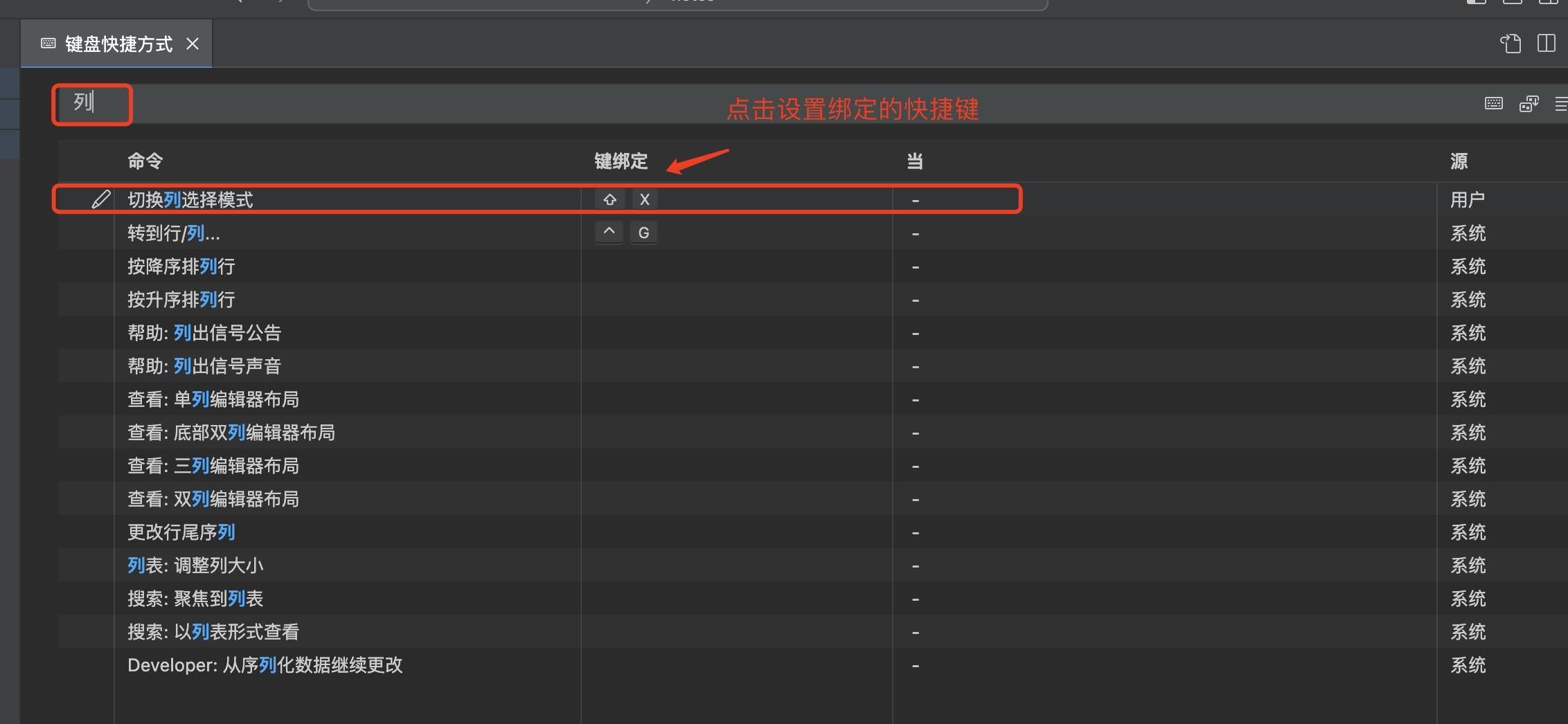
Mac vscode 激活列编辑模式
列编辑模式在批量处理多行文本时,非常有效,但 vscode 默认情况下,又没有激活,因此记录一下启动方法: 激活列编辑模式 然后就可以使用 Alt(Mac 上是 Option 或 Command 键) 鼠标左键 滑动选择了…...

深度学习:GPT-1的MindSpore实践
GPT-1简介 GPT-1(Generative Pre-trained Transformer)是2018年由Open AI提出的一个结合预训练和微调的用于解决文本理解和文本生成任务的模型。它的基础是Transformer架构,具有如下创新点: NLP领域的迁移学习:通过最…...

前端图像处理(一)
目录 一、上传 1.1、图片转base64 二、图片样式 2.1、图片边框【border-image】 三、Canvas 3.1、把canvas图片上传到服务器 3.2、在canvas中绘制和拖动矩形 3.3、图片(同色区域)点击变色 一、上传 1.1、图片转base64 传统上传: 客户端选择图片…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...
