2024-11-19 kron积
若A=[a11 a12;
a21 a22];
B=[b11 b12;
b21 b22];
则C=[a11*b11 a12*b11 a21*b11 a22*b11;
a11*b12 a12*b12 a21*b12 a22*b12;
a11*b21 a12*b21 a21*b21 a22*b21;
a11*b22 a12*b22 a21*b22 a22*b22]
用MATLAB实现
方法1:
A = [a11 a12; a21 a22];
B = [b11 b12; b21 b22];C = zeros(4, 4); % 初始化矩阵C的大小为4x4,填充值为0% 计算矩阵C的每个元素
C(1,:) = A(1,:) .* B(1,:);
C(2,:) = A(1,:) .* B(2,:);
C(3,:) = A(2,:) .* B(1,:);
C(4,:) = A(2,:) .* B(2,:);方法2:
可以使用矩阵运算来简化这个过程,因为矩阵C实际上是由A的行与B的列的外积组成的块矩阵:
A = [a11 a12; a21 a22];
B = [b11 b12; b21 b22];C = [A(1,:) * B'; A(2,:) * B'];方法3:
kron 函数计算的是Kronecker积,它将矩阵A的每个元素与矩阵B相乘
A = [a11 a12; a21 a22];
B = [b11 b12; b21 b22];C = kron(A, B);方法4:
以下是使用四个嵌套的 for 循环来构建矩阵C的MATLAB代码
A = [a11 a12; a21 a22];
B = [b11 b12; b21 b22];C = zeros(4, 4); % 初始化一个4x4的矩阵C% 四个嵌套的for循环来填充矩阵C
for i = 1:2for j = 1:2for k = 1:2for l = 1:2C((i-1)*2+k, (j-1)*2+l) = A(i,j) * B(k,l);endendend
end顺便补个图
% 定义新的变量范围
r_prime = linspace(-1, 1, 400); % r' 从 -1 到 1
theta_prime = linspace(-1, 1, 400); % θ' 从 -1 到 1% 创建网格
[R_prime, Theta_prime] = meshgrid(r_prime, theta_prime);% 转换 r' 和 θ' 回 r 和 θ
r = (R_prime + 1.5) / 2;
theta = pi / 2 * (Theta_prime + 1) / 2;% 计算 Ur'
Ur_prime = (r.^6) .* ((sin(theta)).^4 + (cos(theta)).^4).^(-3/2) .* (cos(theta)).^3 .* (sin(theta)).^3 .* (r.^4 - 1).^3 .* (r.^4 - 1/16).^3;% 处理 r^4 和 θ^4 超出范围的情况
Ur_prime((r.^4 <= 1/16) | (r.^4 >= 1)) = NaN;% 绘制图像
figure;
meshc(R_prime, Theta_prime, Ur_prime);
xlabel('r''');
ylabel('θ''');
zlabel('Ur''');
title('3D plot of Ur''(r'', θ'')');
相关文章:

2024-11-19 kron积
若A[a11 a12; a21 a22]; B[b11 b12; b21 b22]; 则C[a11*b11 a12*b11 a21*b11 a22*b11; a11*b12 a12*b12 a21*b12 a22*b12; a11*b21 a12*b21 a21*b21 a22*b21; a11*b22 a12*b22 a21*b22 a22*b22] 用MATLAB实现 方法1: A [a11 a12; a21 a22]; B [b11 b12; b21 b22]…...
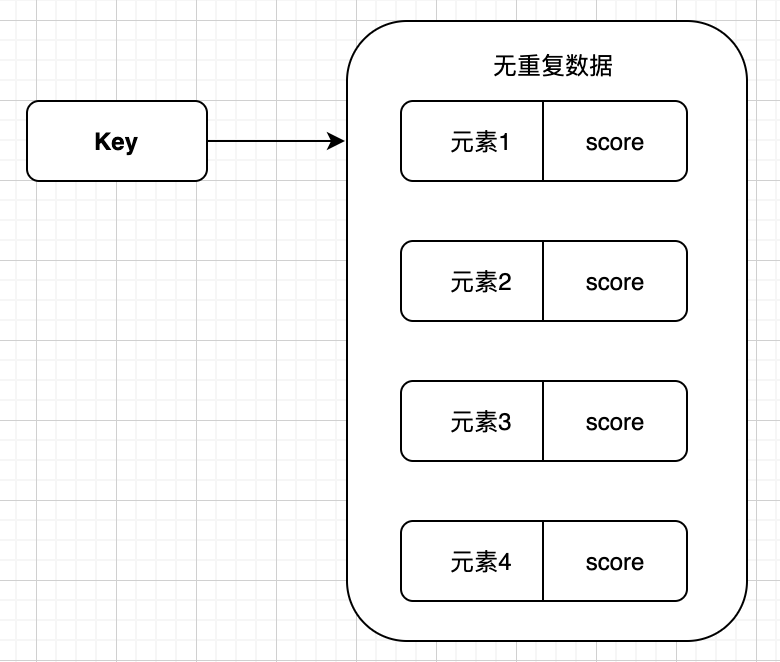
Redis ⽀持哪⼏种数据类型?适⽤场景,底层结构
目录 Redis 数据类型 一、String(字符串) 二、Hash(哈希) 三、List(列表) 四、Set(集合) 五、ZSet(sorted set:有序集合) 六、BitMap 七、HyperLogLog 八、GEO …...

树莓派2 安装raspberry os 并修改成固定ip
安装 安装raspberry os 没啥说的,到树莓派官网,下载制作启动映像盘的软件: https://www.raspberrypi.com/software/ 下载后,直接安装该软件,然后运行,选择好开发板的型号和操作系统型号,按照…...

11月第3周AI资讯
阅读时间:3-4min 更新时间:2024.9.9-2024.9.13 目录 DIAMOND:扩散模型在世界构建中的应用 阿里云推出Qwen2.5-Turbo:高效长文本处理,性价比卓越 微软:AI已实现几乎无限的记忆 Comfyui_Object_Migration一致性换衣模型 DeepSeek发布R1-Lite-Preview:推理AI竞争愈发…...
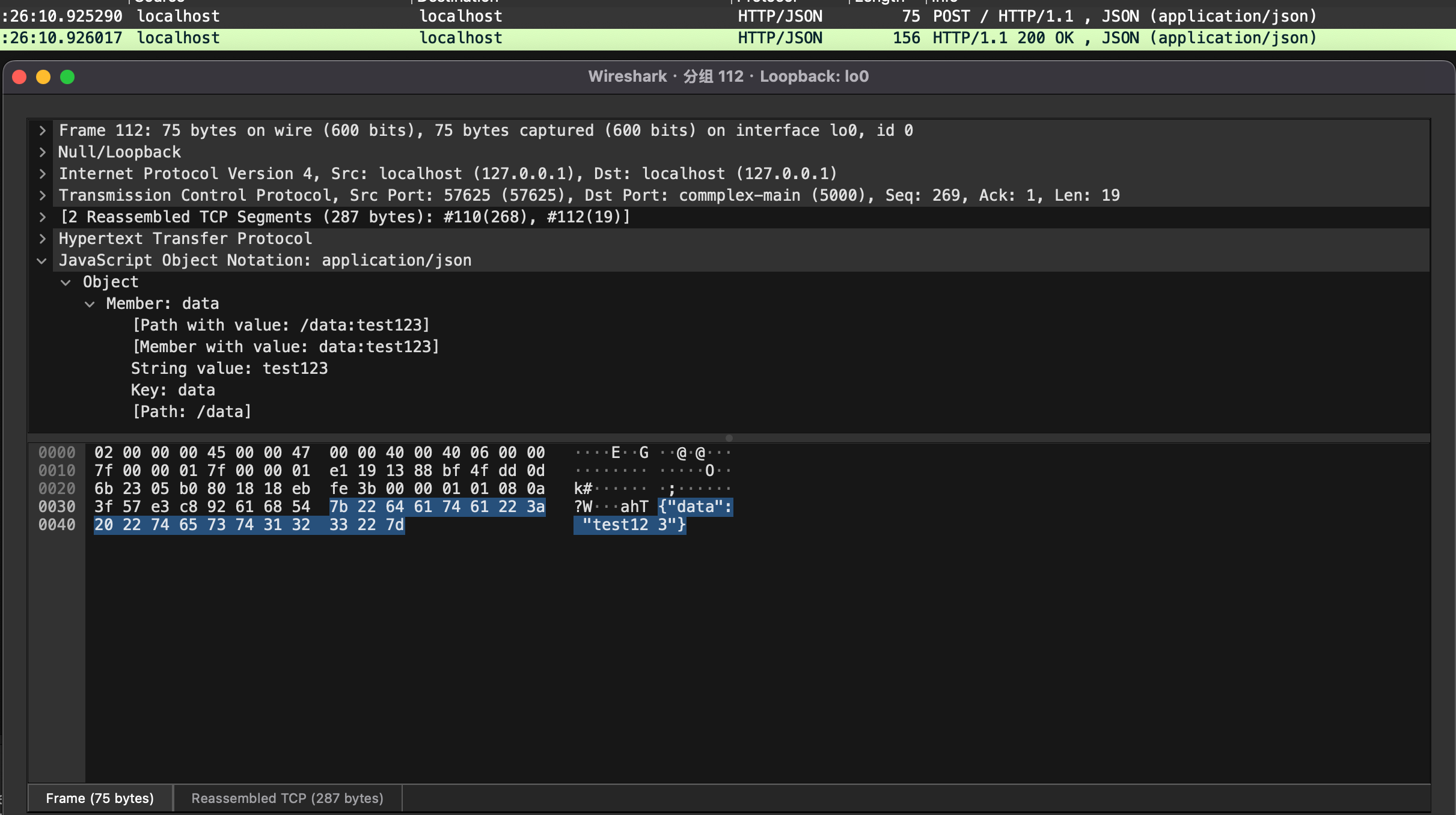
一次封装,解放双手:Requests如何实现0入侵请求与响应的智能加解密
引言 之前写了 Requests 自动重试的文章,突然想到,之前还用到过 Requests 自动加解密请求的逻辑,分享一下。之前在做逆向的时候,发现一般医院的小程序请求会这么玩,请求数据可能加密也可能不加密,但是返回…...

Notepad++--在开头快速添加行号
原文网址:Notepad--在开头快速添加行号_IT利刃出鞘的博客-CSDN博客 简介 本文介绍Notepad怎样在开头快速添加行号。 需求 原文件 想要的效果 方法 1.添加点号 Alt鼠标左键,从首行选中首列下拉,选中需要添加序号的所有行的首列ÿ…...

Python和MATLAB示例临床因素分析
🌵Python片段 为了演示临床因素的分析,让我们模拟一个数据集并执行一些基本的统计和机器学习分析。我们将重点关注以下步骤: 模拟数据集:创建具有年龄、性别、BMI、吸烟状况和疾病结果等特征的临床数据。描述性统计:…...

嵌入式硬件实战基础篇(二)-稳定输出3.3V的太阳能电池-无限充放电
引言:本内容主要用作于学习巩固嵌入式硬件内容知识,用于想提升下述能力,针对学习稳压芯片和电容以及电池之间的运用,对于硬件PCB以及原理图的练习和前面硬件篇的实际运用;太阳能是一种清洁、可再生的能源,广…...

【数据结构】树——链式存储二叉树的基础
写在前面 书接上文:【数据结构】树——顺序存储二叉树 本篇笔记主要讲解链式存储二叉树的主要思想、如何访问每个结点、结点之间的关联、如何递归查找每个结点,为后续更高级的树形结构打下基础。不了解树的小伙伴可以查看上文 文章目录 写在前面 一、链…...

STM32-- keil常见报错与解决办法
调试问题 1. keil在线调试需要点击好几次运行才可以运行,要是直接下载程序直接就不运行。 解决:target里面的use microlib要勾选,因为使用了printf。 keil在线调试STM32,点三次运行才能跑到main的问题解决。 keil在线调试STM32…...
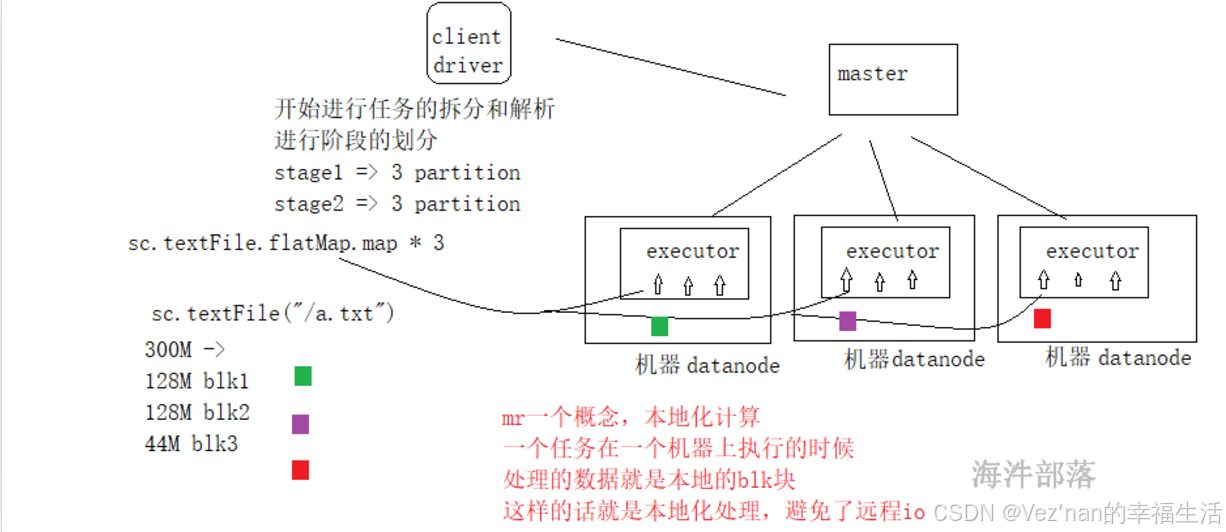
【大数据学习 | Spark-Core】RDD的概念与Spark任务的执行流程
1. RDD的设计背景 在实际应用中,存在许多迭代式计算,这些应用场景的共同之处是,不同计算阶段之间会重用中间结果,即一个阶段的输出结果会作为下一个阶段的输入。但是,目前的MapReduce框架都是把中间结果写入到HDFS中&…...

一文读懂埋阻埋容工艺
PCB 埋阻埋容工艺是一种在 PCB 板内部埋入电阻和电容的工艺。通常情况下, PCB 上电阻和电容都是通过贴片技术直接焊接在板面上的,而埋阻埋容工艺则将电 阻和电容嵌入到 PCB 板的内部层中,这种印制电路板,其自下而上依次包括第一介电 层,隐埋电…...
)
mysql 数据表导出为 markdown(附 go 语言 gorm 的实际使用)
前言 通常业务系统开发中,数据库的设计与维护是至关重要的环节。而数据库的文档化则是确保团队成员之间有效沟通、快速理解系统架构的基础。 但目前数据文档都是手动写的,耗时费力,由于当前项目使用的是 mysql 作为存储引擎,找找…...

本地云存储 MinIO 中修改用户密码
本地云存储 MinIO 中修改用户密码 MinIO 中修改用户密码前提条件步骤 1:安装 MinIO Client对于 Linux/macOS:对于 Windows: 步骤 2:配置 MinIO Client步骤 3:查看现有用户步骤 4:修改用户密码步骤 5&#x…...

go项目中比较好的实践方案
工作两年来,我并未遇到太大的挑战,也没有特别值得夸耀的项目。尽管如此,在日常的杂项工作中,我积累了不少心得,许多实践方法也在思考中逐渐得到优化。因此,我在这里记录下这些心得。 转发与封装 这个需求…...
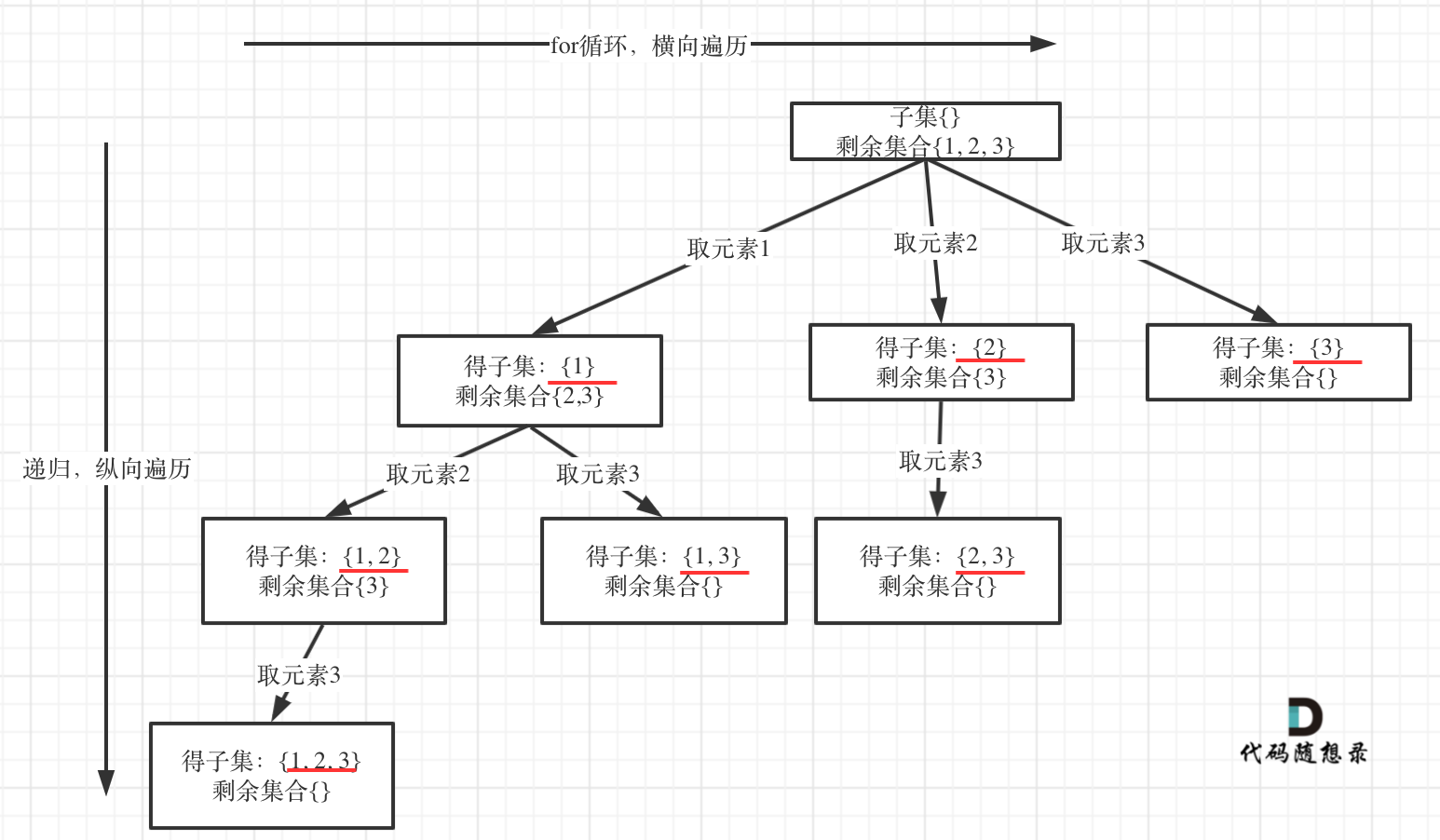
回溯法基础入门解析
回溯法 前 言 回溯法也可以叫做回溯搜索法,它是一种搜索的方式。回溯是递归的副产品,只要有递归就会有回溯。回溯法,一般可以解决如下几种问题: 组合问题:N个数里面按一定规则找出k个数的集合切割问题:一…...
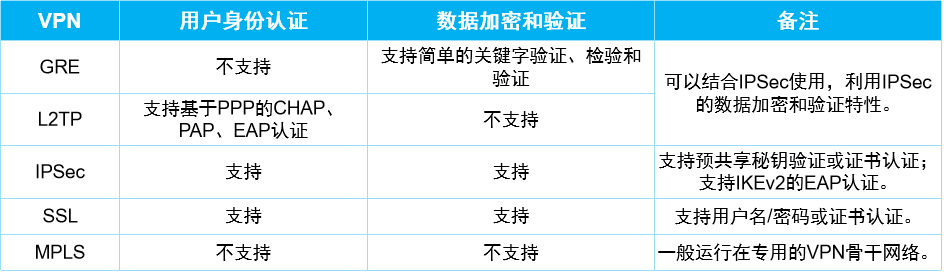
计算机网络-VPN虚拟专用网络概述
前面我们学习了在企业内部的二层交换机网络、三层路由网络包括静态路由、OSPF、IS-IS、NAT等,现在开始学习下VPN(Virtual Private Network,虚拟专用网络),其实VPN可能很多人听到第一反应就是梯子,但是其实这…...

信创时代的数据库之路:2024 Top10 国产数据库迁移与同步指南
数据库一直是企业数字化和创新的重要基础设施之一。从传统的关系型数据库到非关系型数据库、分析型数据库,再到云数据库和多模数据库,这一领域仍在持续变革中,各种新型数据库产品涌现,数据管理的能力和应用场景也由此得到了扩展。…...

自制游戏:监狱逃亡
第一个游戏,不喜勿喷: #include<bits/stdc.h> #include<windows.h> using namespace std; int xz; int ruond_1(int n){if(xz1){printf("撬开了,但站在你面前的是俄罗斯内务部特种部队的奥摩大帝,你被九把加特…...

小雪时节,阴盛阳衰,注意禁忌
宋张嵲《小雪作》 霜风一夜落寒林,莽苍云烟结岁阴。 把镜渐无勋业念,爱山唯驻隐沦心。 冰花散落衡门静,黄叶飘零一迳深。 世乱身穷无可奈,强将悲慨事微吟。 网络图片:小雪时节 笔者禁不住喟然而叹:“冰…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...
。】2022-5-15)
【根据当天日期输出明天的日期(需对闰年做判定)。】2022-5-15
缘由根据当天日期输出明天的日期(需对闰年做判定)。日期类型结构体如下: struct data{ int year; int month; int day;};-编程语言-CSDN问答 struct mdata{ int year; int month; int day; }mdata; int 天数(int year, int month) {switch (month){case 1: case 3:…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

条件运算符
C中的三目运算符(也称条件运算符,英文:ternary operator)是一种简洁的条件选择语句,语法如下: 条件表达式 ? 表达式1 : 表达式2• 如果“条件表达式”为true,则整个表达式的结果为“表达式1”…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...
