刷题笔记15
问题描述
小M和小F在玩飞行棋。游戏结束后,他们需要将桌上的飞行棋棋子分组整理好。现在有 N 个棋子,每个棋子上有一个数字序号。小M的目标是将这些棋子分成 M 组,每组恰好5个,并且组内棋子的序号相同。小M希望知道是否可以按照这种方式对棋子进行分组。
例如,假设棋子序号为 [1, 2, 3, 4, 5],虽然只有5个棋子,但由于序号不同,因此不能形成有效的分组。如果序号是 [1, 1, 1, 1, 1, 2, 2, 2, 2, 2],则可以形成两个有效分组,因此输出为 True。
测试样例
样例1:
输入:
nums = [1, 2, 3, 4, 5]
输出:"False"
样例2:
输入:
nums = [1, 1, 1, 1, 2, 1, 2, 2, 2, 2]
输出:"True"
样例3:
输入:
nums = [5, 5, 5, 5, 5, 5, 5, 5, 5, 5]
输出:"True"
样例4:
输入:
nums = [7, 7, 7, 8, 8, 8, 8, 8, 7, 7]
输出:"True"
样例5:
输入:
nums = [9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9]
输出:"False"
解决方案分析
- 出现次数计数:首先,我们需要统计每个数字的出现次数。
- 检查能否分组:对于每个数字的出现次数,如果某个数字的出现次数不能被 5 整除,则无法分成有效的组,直接返回
"False"。 - 判断是否可以分成 M 组:如果所有数字的出现次数都能被 5 整除,则返回
"True",表示可以按要求分组。
步骤
- 统计频率:使用一个哈希表(或字典)来统计每个数字出现的次数。
- 判断条件:遍历统计的次数,如果某个数字的出现次数不能被 5 整除,直接返回
"False"。 - 返回结果:如果所有数字的出现次数都能被 5 整除,返回
"True"。
代码实现
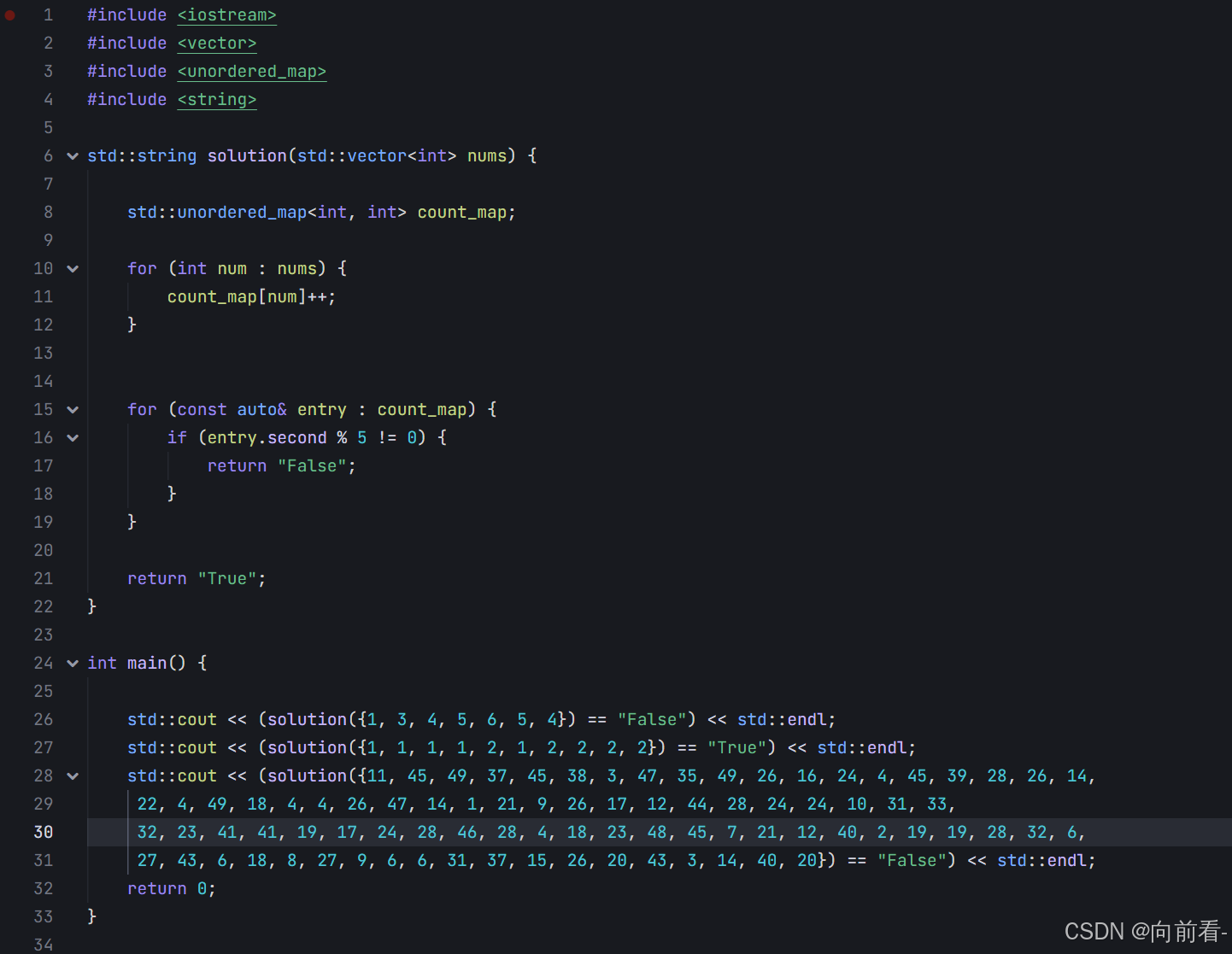
代码说明
- unordered_map:我们使用了 C++ 标准库中的
unordered_map来存储每个数字及其出现的次数。它提供了快速的查找、插入和删除操作。 - 循环遍历数字:我们遍历
nums数组,将每个数字的出现次数统计到count_map中。 - 检查条件:遍历
count_map中的每个数字和其对应的计数,判断是否能被 5 整除。如果有任何数字的出现次数不能被 5 整除,返回"False"。 - 最终返回:如果所有数字的出现次数都能被 5 整除,则返回
"True"。
测试用例解析
- 样例 1:
{1, 2, 3, 4, 5},每个数字出现一次,无法分成组,输出"False"。 - 样例 2:
{1, 1, 1, 1, 2, 1, 2, 2, 2, 2},1 的出现次数是 5,2 的出现次数是 5,能分成 2 组,输出"True"。 - 样例 3:
{5, 5, 5, 5, 5, 5, 5, 5, 5, 5},每个数字 5 出现 10 次,能分成 2 组,输出"True"。 - 样例 4:
{7, 7, 7, 8, 8, 8, 8, 8, 7, 7},7 和 8 都出现了 5 次,能分成 2 组,输出"True"。 - 样例 5:
{9, 9, 9, 9, 9, 9, 9, 9, 9, 9, 9},数字 9 出现了 11 次,不能被 5 整除,输出"False"。
时间复杂度
- 统计数字频率需要遍历一次数组,时间复杂度为 O(N),其中 N 是数组的长度。
- 遍历哈希表的键值对,最多需要 O(K) 的时间,其中 K 是不同数字的个数(在最坏情况下 K = N)。
- 总体时间复杂度为 O(N),空间复杂度为 O(K)。
哈哈--
相关文章:

刷题笔记15
问题描述 小M和小F在玩飞行棋。游戏结束后,他们需要将桌上的飞行棋棋子分组整理好。现在有 N 个棋子,每个棋子上有一个数字序号。小M的目标是将这些棋子分成 M 组,每组恰好5个,并且组内棋子的序号相同。小M希望知道是否可以按照这…...
【LeetCode热题100】队列+宽搜
这篇博客是关于队列宽搜的几道题,主要包括N叉树的层序遍历、二叉树的锯齿形层序遍历、二叉树最大宽度、在每个数行中找最大值。 class Solution { public:vector<vector<int>> levelOrder(Node* root) {vector<vector<int>> ret;if(!root) …...

【阵列信号处理】相干信号和非相干信号生成
文章目录 一、总结二、知识点相干(coherent)和非相干(incoherent)信号相干信号生成代码 相关信号(correlated signal)相关信号生成代码 正交信号定义 本文记录博主的科研日记。如果对博主的其他文章感兴趣&…...

React 组件生命周期
React 组件生命周期 React 组件生命周期是React框架中一个核心概念,它描述了一个组件从创建到销毁的过程。理解组件生命周期对于高效开发React应用至关重要,因为它允许开发者在一个组件的不同阶段执行特定的逻辑。本文将详细介绍React组件的生命周期方法,并解释它们在组件的…...
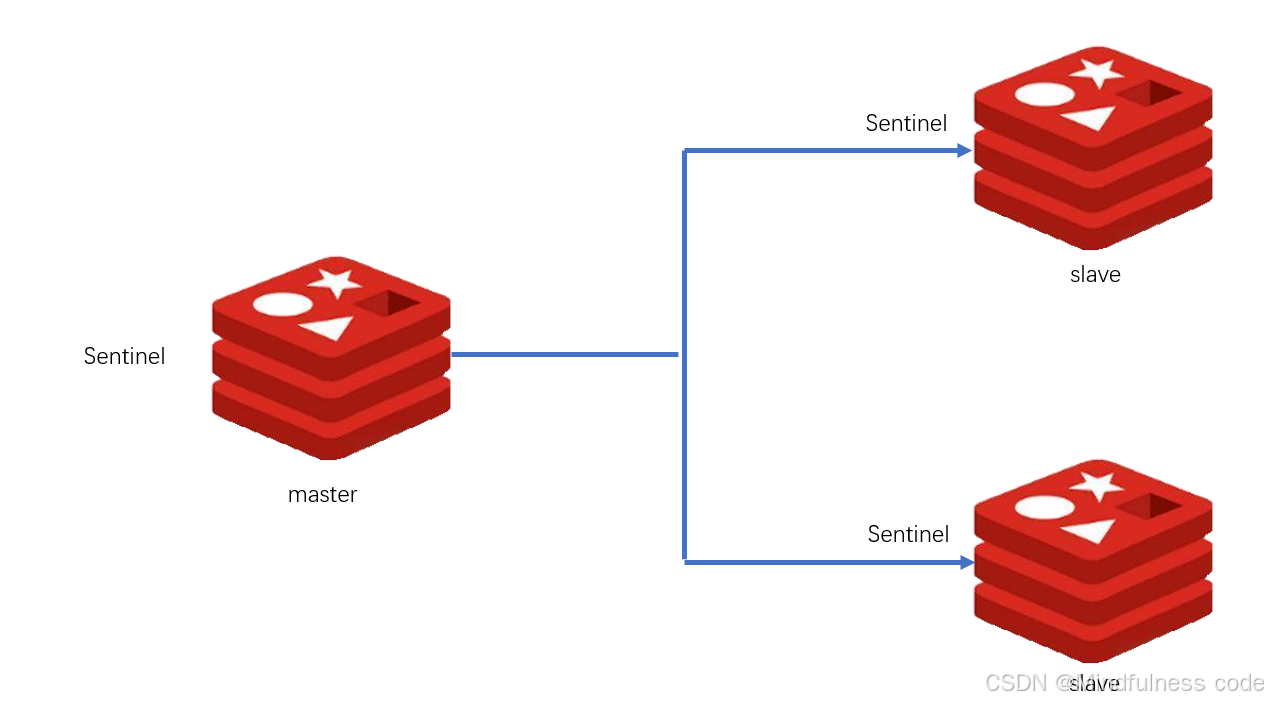
Kylin Server V10 下基于Sentinel(哨兵)实现Redis高可用集群
一、什么是哨兵模式 Redis Sentinel 是一个分布式系统,为 Redis 提供高可用性解决方案。可以在一个架构中运行多个 Sentinel 进程(progress)这些进程使用流言协议(gossip protocols)来接收关于主服务器是否下线信息,并使用投票协议(agreement protocols)来决定是否执行…...
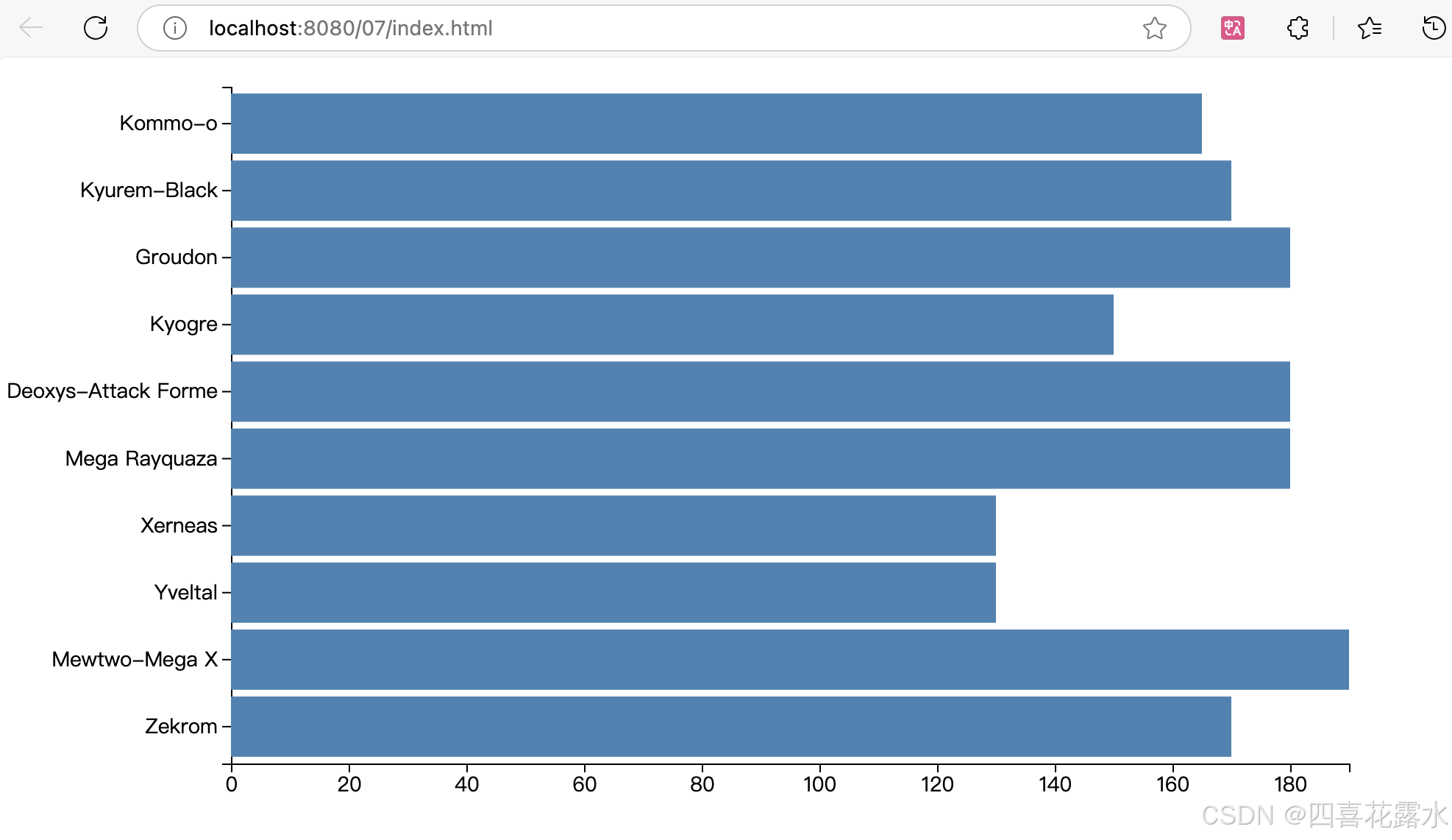
07-Making a Bar Chart with D3.js and SVG
课程链接 Curran的课程,通过 D3.js 的 scaleLinear, max, scaleBand, axisLeft, axisBottom,根据 .csv 文件生成一个横向柱状图。 【注】如果想造csv数据,可以使用通义千问,关于LinearScale与BandScale不懂的地方也可以在通义千…...

硅谷甄选前端项目环境配置笔记
此教程来自于尚硅谷 文章目录 **此教程来自于尚硅谷**硅谷甄选运营平台一、搭建后台管理系统模板1.1项目初始化1.1.1环境准备1.1.2初始化项目 1.2项目配置一、eslint配置1.1vue3环境代码校验插件1.2修改.eslintrc.cjs配置文件1.3.eslintignore忽略文件1.4运行脚本 二、配置**pr…...

6.7机器学习期末复习题
空间 样本空间 就是属性的所有可能情况,包括了一切可能出现或不可能出现的所有样本情况 版本空间&假设空间 假设空间就是在样本空间的基础上,给所有属性都加了一个通配符,表示任意即可;以及加上了一个空集,表示…...

1123--日期类
目录 一 java 1. Date类 2. calendar类 3. 第三代日期类‘ 3.1 常用方法 3.2 格式化操作 一 java 1. Date类 2. calendar类 3. 第三代日期类‘ 3.1 常用方法 3.2 格式化操作...
YOLOV5 /onnx模型转换成rknn
上两篇文章讲述了pytorch模型下best.pt转换成onnx模型,以及将onnx进行简化成为best-sim.onnx, 接下来这篇文章讲述如何将onnx模型转换成rknn模型,转换成该模型是为了在rk3568上运行 1.创建share文件夹 文件夹包含以下文件best-sim.onnx,rknn-tookit2-…...
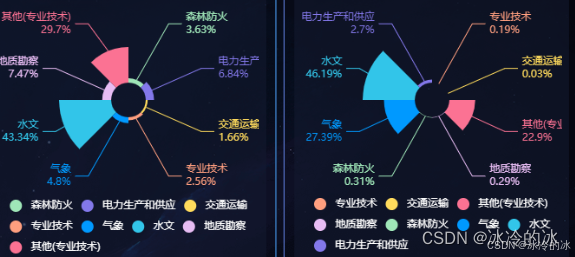
Echarts+VUE饼图的使用(基础使用、多个饼图功能、单组饼图对应颜色使用)
安装:npm install echarts --save 配置:main.js // 引入echarts import * as echarts from echarts Vue.prototype.$echarts echarts一、基础饼图(直接拷贝就能出效果) <div class"big-box" ref"demoEhart"><…...
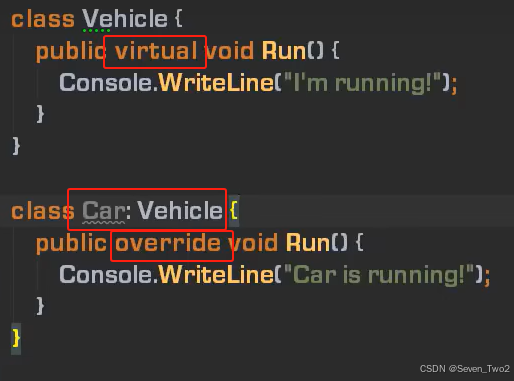
刘铁猛C#入门 026 重写与多态
类的继承 类成员的“横向扩展”(成员越来越多)类成员的“纵向扩展”(行为改变,版本增高)类成员的隐藏(不常用)重写与隐藏的发生条件:函数成员,可见,签名一致 函数成员:方法 、属性可见:父类修饰符是public protected …...

《筑牢安全防线:培养 C++安全编程思维习惯之道》
在当今数字化飞速发展的时代,软件安全的重要性已提升到前所未有的高度。C作为一种广泛应用于系统开发、游戏制作、高性能计算等众多领域的编程语言,其程序的安全性更是关乎重大。培养 C安全编程的思维习惯,不仅是开发者个人能力提升的关键&am…...
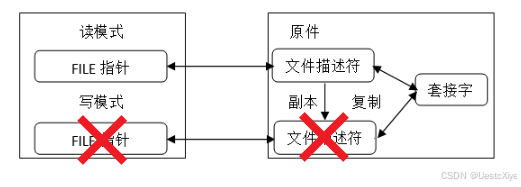
《TCP/IP网络编程》学习笔记 | Chapter 16:关于 I/O 流分离的其他内容
《TCP/IP网络编程》学习笔记 | Chapter 16:关于 I/O 流分离的其他内容 《TCP/IP网络编程》学习笔记 | Chapter 16:关于 I/O 流分离的其他内容分离 I/O 流2 次 I/O 流分离分离「流」的好处「流」分离带来的 EOF 问题 文件描述符的的复制和半关闭终止「流」…...

单片机学习笔记 5. 数码管静态显示
更多单片机学习笔记:单片机学习笔记 1. 点亮一个LED灯单片机学习笔记 2. LED灯闪烁单片机学习笔记 3. LED灯流水灯单片机学习笔记 4. 蜂鸣器滴~滴~滴~ 目录 0、实现的功能 1、Keil工程 1-1 数码管显示原理 1-2 静态与动态显示 1-3 74HC573锁存器的工作原理 1-…...

ValueError: not enough values to unpack (expected 2, got 1) 解决方案
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。喜欢通过博客创作的方式对所学的…...

java基础知识(常用类)
一、包装类(Wrapper) (1)包装类与基本数据的转换 装箱:基本类型->包装类型 拆箱:包装类型->基本类型 java5以后是自动装箱和拆箱的方式,自动装箱底层调用的是valueOf方法,比如Integer.…...
Selenium+Java(19):使用IDEA的Selenium插件辅助超快速编写Pages
前言 或是惊叹于Selenium对于IDEA的支持已经达到了这样的地步,又或是由于这个好用的小工具的入口就在那里,它已经陪伴了我这么久,而我这么久的时间却都没有发现它。在突然发现这个功能的一瞬间,真的是喜悦感爆棚,于是赶快写下了这篇文章。希望可以帮助到其他同样在做UI自动…...

决策树分类算法【sklearn/决策树分裂指标/鸢尾花分类实战】
决策树分类算法 1. 什么是决策树?2. DecisionTreeClassifier的使用(sklearn)2.1 算例介绍2.2 构建决策树并实现可视化 3. 决策树分裂指标3.1 信息熵(ID3)3.2 信息增益3.3 基尼指数(CART) 4. 代码…...

深入理解 Spring Boot 的 WebApplicationType
1. 前言 在 Spring Boot 应用程序启动过程中,WebApplicationType 是一个重要的概念,它决定了应用程序是以 Web 应用程序的形式运行还是以非 Web 应用程序的形式运行。本文将详细探讨 WebApplicationType 的工作机制及其在实际项目中的应用。 2. 什么是 WebApplicationType?…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

聊一聊接口测试的意义有哪些?
目录 一、隔离性 & 早期测试 二、保障系统集成质量 三、验证业务逻辑的核心层 四、提升测试效率与覆盖度 五、系统稳定性的守护者 六、驱动团队协作与契约管理 七、性能与扩展性的前置评估 八、持续交付的核心支撑 接口测试的意义可以从四个维度展开,首…...
