算法模板2:位运算+离散化+区间合并
文章目录
- 1.6 位运算
- **位运算的常见应用**
- 1.7 离散化
- **经典离散化题目例子**
- **1. 区间合并和覆盖长度问题**
- **2. 区间查询与修改**
- **3. 动态求第 K 小值**
- **4. 区间最大重叠次数**
- **5. 动态逆序对计数**
- **6. 二维区间问题**
- **7. 模拟车流/时间段事件**
- **8. 区间众数统计**
- **具体例题**
- 1.8 区间合并
1.6 位运算
位运算是直接在二进制位上进行操作的运算。位运算通常用于优化算法,尤其是当涉及到数字处理、快速计算和空间优化
- 按位与
&(AND)
-
操作规则:当两个二进制数的对应位都为1时,结果才为1,否则为0。
1010 & 1101 ------ 1000- 检查某一位是否为1: 例如,
n & (1 << k)判断第k位是否为1。如果为1,结果不为0;否则为0。 - 清除最低位的1:
n & (n - 1)会将n的最低位1变成0。
- 检查某一位是否为1: 例如,
- 按位或
|(OR)
-
操作规则:当两个二进制数的对应位中至少有一个为1时,结果为1。
1010 | 1101 ------ 1111- 设置某一位为1:
n | (1 << k)将第k位置为1。
- 设置某一位为1:
- 按位异或
^(XOR)
-
操作规则:当两个二进制数的对应位相异时,结果为1,否则为0。
1010 ^ 1101 ------ 0111- 翻转某一位:
n ^ (1 << k)将第k位的值翻转(1变成0,0变成1)。 - 检查两个数是否相等:
a ^ b == 0表示a与b相等。
- 翻转某一位:
- 按位非
~(NOT)
-
操作规则:对每一位取反,1变成0,0变成1。
~ 1010 ------ 0101
- 左移
<<(Left Shift)
-
操作规则:将二进制数的所有位向左移动指定的位数,左移时低位补0,高位丢弃。
1010 << 1 = 10100- 乘以2:
n << 1相当于将n乘以2。 - 高速计算乘法:左移可以用来快速计算n的2的幂次方倍数。
- 乘以2:
- 右移
>>(Right Shift)
-
操作规则:将二进制数的所有位向右移动指定的位数,右移时高位补符号位(有符号数时补1,没符号数时补0)。
1010 >> 1 = 0101- 除以2:
n >> 1相当于将n除以2。 - 高速计算除法:右移可以用来快速计算n的2的幂次方除法。
- 除以2:
- 获取某一位的值
n >> k & 1
- 说明:
n >> k将n右移k位,然后与1做按位与运算,这样可以获取n的第k位数字(0或1)。
- 获取n的最后一位1
lowbit(n) = n & -n
- 说明:
n & -n用来得到n的最后一位1。例如,n = 12 (1100)时,lowbit(n)的结果为4 (0100)。-n是n的二进制补码表示,n & -n会保留n的最后一位1,并将其他所有位清零。
位运算的常见应用
- 判断奇偶性:
- 通过
n & 1判断n是否为奇数(如果结果是1则n为奇数)。
- 通过
- 快速计算2的幂:
- 使用
1 << k来计算2^k。
- 使用
- 检查二进制表示中是否只有一个1:
n & (n - 1) == 0可以检查n是否为2的幂(如果n只包含一个1)。
- 统计二进制中1的个数:
__builtin_popcount(n)或while (n) {n &= (n - 1);},每次去掉最右边的1。
- 交换两个数:
a ^= b; b ^= a; a ^= b;可以用异或交换两个数。
- 清除低位的1:
n & (n - 1)会把n的最低位的1清除。
- 模拟集合:
- 通过位运算可以模拟集合的操作,如
set、union、intersection等。例如,n可以表示一个集合,其中第k位表示是否包含元素k。
- 通过位运算可以模拟集合的操作,如
1.7 离散化
核心作用:将数值范围较大的数据映射到一个较小的连续整数范围,便于在数组、前缀和、差分、树状数组、线段树等数据结构中操作。
主要解决值域大、数据稀疏的问题,结合其他算法实现高效求解,如扫描线、差分数组、树状数组和线段树等。
vector<int> alls; // 存储所有待离散化的值
sort(alls.begin(), alls.end()); // 将所有值排序
alls.erase(unique(alls.begin(), alls.end()), alls.end()); // 去掉重复元素// 二分求出x对应的离散化的值
int find(int x) // 找到第一个大于等于x的位置
{int l = 0, r = alls.size() - 1;while (l < r){int mid = l + r >> 1;if (alls[mid] >= x) r = mid;else l = mid + 1;}return r + 1; // 映射到1, 2, ...n
}
经典离散化题目例子
1. 区间合并和覆盖长度问题
题目:给定 n 个区间 [li,ri][l_i, r_i],求所有区间的覆盖总长度(去重后的长度)。
-
分析:原区间可能范围很大(如 [1,109][1, 10^9]),无法直接操作。通过离散化,将所有区间端点压缩到较小范围。
-
思路
- 离散化所有区间的端点。
- 用差分数组或扫描线记录区间变化,统计覆盖长度。
2. 区间查询与修改
题目:有 n 个点,每次给区间 [l,r][l, r] 增加一个值 cc,并查询某个点的最终值。
-
分析:区间范围过大(如 1∼1091 \sim 10^9),通过离散化压缩到有限范围。
-
思路
- 离散化所有可能的坐标。
- 使用差分数组、树状数组或线段树进行区间操作。
3. 动态求第 K 小值
题目:有 n 个操作,每次插入一个值或查询当前数据的第 k 小值。
-
分析:可能有很大的值范围(如 [1,109][1, 10^9]),通过离散化解决大范围权值问题。
-
思路
- 离散化所有插入的值。
- 用树状数组或线段树统计权值频次。
4. 区间最大重叠次数
题目:给定 n 个区间,求区间重叠最多的时间点及重叠次数。
-
分析:时间点范围可能很大,需离散化区间端点。
-
思路
- 离散化所有区间端点。
- 使用扫描线或差分数组统计每个离散点的重叠次数。
5. 动态逆序对计数
题目:给定一个初始数组,每次插入一个值,实时输出数组的逆序对个数。
-
分析:插入值可能范围过大(如 [1,109][1, 10^9]),需离散化值域。
-
思路
- 离散化所有可能的值。
- 用树状数组或线段树动态维护逆序对。
6. 二维区间问题
题目:给定 n 个矩形,求哪些矩形有重叠区域或总覆盖面积。
-
分析:矩形坐标范围可能很大,需对 x 和 y 坐标分别离散化。
-
思路
- 对 x 和 y 轴分别离散化,压缩到二维数组。
- 使用二维差分或扫描线处理。
7. 模拟车流/时间段事件
题目:给定 n 个车辆的进入和离开时间,求某时刻停车场中车辆的数量。
-
分析:时间范围可能很大(如 [1,109][1, 10^9]),需离散化时间点。
-
思路
- 离散化所有进入和离开的时间点。
- 使用差分数组统计每个时间点的车辆变化。
8. 区间众数统计
题目:给定一个数组,支持动态查询任意区间内的众数。
-
分析:值域较大(如 [1,109][1, 10^9]),需离散化元素值。
-
思路
- 离散化数组中的值。
- 用莫队算法或树状数组分块统计。
具体例题
- 区间统计问题:Leetcode 56 合并区间。
- 动态第 k 小问题:Leetcode 315 计算右侧小于当前元素的个数。
- 区间重叠次数:AcWing 1240 最大区间重叠。
- 动态逆序对计数:Leetcode 493 翻转对。
- 二维差分矩阵:AcWing 1226 最大矩形面积。
1.8 区间合并
using PII = pair<int, int>;// 合并区间的函数
void merge(vector<PII> &segs) {vector<PII> res;// 1. 按起点排序,如果起点相同,按终点排序sort(segs.begin(), segs.end());// 2. 初始化st和ed为不可能出现的值int st = -2e9, ed = -2e9;// 3. 遍历所有区间for (auto seg : segs) {if (ed < seg.first) { // 当前区间与前一个区间不重叠if (st != -2e9) res.push_back({st, ed}); // 把上一个区间加入结果st = seg.first; // 更新sted = seg.second; // 更新ed} else { // 当前区间与前一个区间重叠ed = max(ed, seg.second); // 合并区间,更新ed}}// 4. 最后一个区间加入结果if (st != -2e9) res.push_back({st, ed});egs = res; // 更新输入数组
}
相关文章:

算法模板2:位运算+离散化+区间合并
文章目录 1.6 位运算**位运算的常见应用**1.7 离散化**经典离散化题目例子****1. 区间合并和覆盖长度问题****2. 区间查询与修改****3. 动态求第 K 小值****4. 区间最大重叠次数****5. 动态逆序对计数****6. 二维区间问题****7. 模拟车流/时间段事件****8. 区间众数统计** **具…...

钉钉授权登录
一.找开钉钉开发平台【钉钉开放平台 (dingtalk.com)】 二。点击菜单【应用开发】->左边【钉钉应用】->【创建应用】 三。创建应用-》保存成功后,点击自己【新建的应用】,进入详细页面 四。进入应用详细页面。左边【分享设置】 注意:进…...
)
【视频】二维码识别:libzbar-dev、zbar-tools(zbarimg )
1、简介 ZBar可以使用多个方式识别各种条形码和二维码。 支持的格式有:EAN-13/UPC-A、UPC-E、EAN-8、Code 128、Code 93、Code 39、Codabar、Interleaved 2 of 5、QR Code和SQ Code 支持的来源有:视频流、图像文件等 libzbar-dev:二维码识别开发库 zbar-tools(zbarimg …...

C语言中的结构体,指针,联合体的使用
目录 1. 概述2. 定义和初始化3. 成员的使用4. 结构体数组5. 结构体套结构体6. 结构体赋值7. 结构体和指针8. 结构体作为函数参数9. 共用体(联合体)10. typedef就是取别名总结 1. 概述 数组:连续的相同数据类型的集合 结构体:不同…...

基于卡尔曼滤波器的 PID 控制
基于卡尔曼滤波器的PID控制算法结合了经典控制理论和现代信号处理技术。卡尔曼滤波器(Kalman Filter, KF)可以对噪声数据进行平滑处理,从而改善PID控制器的性能,特别是在处理具有噪声和不确定性的系统时。以下是详细的设计过程&am…...

CVE-2022-26201
打开是这么个页面 左上角找到Admin访问 里面有个Add Users,访问一下,能创建用户,有个能上传图片的地方 普通的一句话木马无法访问flag,需要创建一个权限马 <?php system($_GET[1]);phpinfo();?> 因为只能上传jpg形式的文…...

海信Java后端开发面试题及参考答案
TCP 的优点是什么? TCP(Transmission Control Protocol,传输控制协议)是一种面向连接的、可靠的、基于字节流的传输层通信协议,它具有众多优点。 首先,TCP 提供可靠的传输服务。它通过序列号、确认应答、重传机制等确保数据的准确无误传输。例如,在发送数据时,发送方会…...

传智杯 3-初赛:终端
题目描述: 有一天您厌烦了电脑上又丑又没用的终端,打算自己实现一个 Terminal。具体来说,它需要支持如下命令: 1. touch filename:如果名为 filename 的文件不存在,就创建一个这样的文件,如果已经存在同名…...

大数据新视界 -- Hive 数据分区:精细化管理的艺术与实践(上)(7/ 30)
💖💖💖亲爱的朋友们,热烈欢迎你们来到 青云交的博客!能与你们在此邂逅,我满心欢喜,深感无比荣幸。在这个瞬息万变的时代,我们每个人都在苦苦追寻一处能让心灵安然栖息的港湾。而 我的…...

【中间件】Redis
一、什么是Redis Redis是一个开源(BSD许可),内存存储的数据结构服务器,可用作数据库,高速缓存和消息队列代理。它支持字符串、哈希表、列表、集合、有序集合,位图,hyperloglogs等数据类型。内置…...
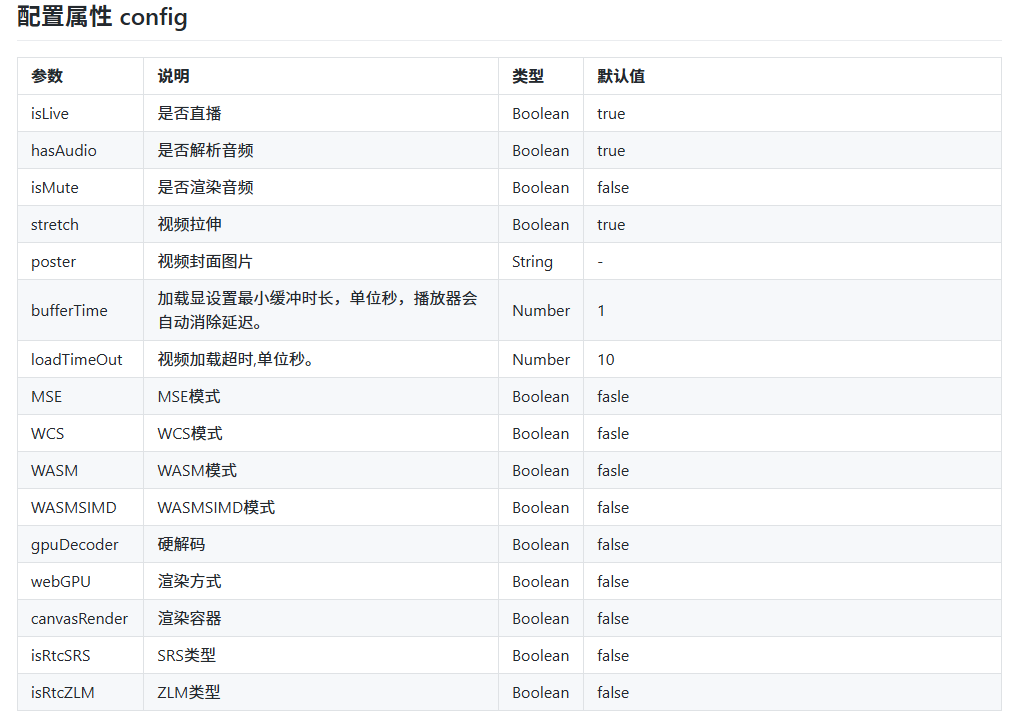
RTSP播放器EasyPlayer.js播放器分辨率高的视频在设置container的宽高较小时,会出现锯齿状的画面效果
流媒体播放器的核心技术及发展趋势展现了其在未来数字生活中的无限潜力。随着技术的不断进步和市场的持续发展,流媒体播放器将在内容创新、用户体验优化以及跨平台互通等方面取得新的突破。对于从业者而言,把握这些趋势并积极应对挑战将是实现成功的关键…...

Java爬虫:获取商品详情的实践之旅
在当今这个信息爆炸的时代,数据的价值日益凸显。对于电商行业来说,商品详情的获取尤为重要,它不仅关系到产品的销售,还直接影响到用户体验。传统的人工获取方式耗时耗力,而自动化的爬虫技术则提供了一种高效解决方案。…...

行业分析---2024年小鹏汽车AI Day及三季度财报
1 背景 在之前的博客中,笔者撰写了多篇行业类分析的文章(科技新能源): 《行业分析---我眼中的Apple Inc.》 《行业分析---马斯克的Tesla》 《行业分析---造车新势力之蔚来汽车》 《行业分析---造车新势力之小鹏汽车》 《行业分析-…...

写时复制,读时加载
实现写时复制,读时加载,原理为,申请内存时,只给一段线性地址空间,并不分配物理内存,当cpu读、写该内存时,发生缺页中,或者写错误,中断处理程序根据前面设置的内容&#x…...

Python和R基因组及蛋白质组学和代谢组学
🌵Python片段 1. 数据处理与清理 基因组病理学的数据通常非常庞大,且可能包括 DNA 或 RNA 测序结果、基因表达数据等。Python 提供了高效的数据处理工具。 工具和库 Pandas: 用于加载、清理和操作数据。Numpy: 用于高效的数值计算。Dask: 用于大规模数…...

selenium环境搭建详细过程
一、准备工作 在开始搭建 Selenium 环境之前,确保具备以下条件: 1.稳定的网络连接: 以便能够下载所需的软件和驱动程序。 2.操作系统基础: 对您的操作系统(如 Windows、Mac 或 Linux)有基本的了解和操…...

Linux知识 - VIM
VI于VIM linux系统里边内置了一个编辑器就叫做vi(visual editor),但vi的功能非常有限,所以一般Linux的使用人员会选择一个比vi更强大的编辑器vim Vim的三种工作模式 输入模式 在正常模式中按下别字母键,会进入插入模式…...

【数据结构】链表重难点突破
目录 一、链表的概念 二、链表的实现 2.1 链表的构建 2.2 从链表头部添加元素 2.3 从链表尾部添加元素 2.4 链表任意位置添加元素 2.5 常规方法实现 2.6 获取指定位置的元素 2.7 获取指定元素的位置 2.8 修改链表中某一节点 2.9 删除链表的头结点 2.10 删除链表的尾…...

大宗商品行业区块链应用
应用场景 区块链技术具有透明性、去中心化、不可篡改等特点,因此可以在大宗商品定价方面得到应用。通过区块链技术,相关交易的各方可以在无需依赖中心化第三方的情况下,实时、准确地获取定价信息。这种技术的应用能够提高效率、降低成本、提…...

Varjo:垂直起降机混合现实培训解决方案
混合电动垂直起降机(VTOL)作为一种新型的航空运输机具有超越传统汽车的安全性、与飞机相当的速度以及无与伦比的灵活起降功能。电动垂直起降机能够在建筑顶部、直升机场或是没有跑道的地区起飞或降落,且排放要远远低于由航空汽油驱动的传统飞…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...
