霍曼转移方法介绍
霍曼转移方法介绍
背景
在航天工程中,轨道转移是指航天器从一个轨道移动到另一个轨道的过程。为了高效利用燃料并缩短转移时间,科学家们开发了多种轨道转移方法。其中,霍曼转移(Hohmann Transfer)因其燃料效率高、计算简单而被广泛应用于卫星部署和行星探测任务中。霍曼转移方法由德国工程师沃尔特·霍曼(Walter Hohmann)于1925年首次提出,成为轨道力学中的经典理论。
霍曼转移方法的基本原理
霍曼转移方法是一种利用椭圆轨道实现两个圆形轨道之间转移的双点燃方法。具体而言,航天器需要在出发轨道和目标轨道上各施加一次脉冲,以改变其运动轨迹,使其从初始轨道转移到目标轨道。这种方法假设转移过程中轨道为椭圆形,且转移轨道与初始和目标轨道在转移点切线相同。
公式推导
1. 轨道半长轴的计算
霍曼转移轨道是连接初始轨道和目标轨道的椭圆轨道,其半长轴 ( a t a_t at) 为两轨道半径 ( r 1 r_1 r1, r 2 r_2 r2) 的平均值:
a t = r 1 + r 2 2 a_t = \frac{r_1 + r_2}{2} at=2r1+r2
2. 霍曼转移所需的变轨速度 ( Δ V \Delta V ΔV)
霍曼转移需要在初始轨道和目标轨道的切点分别施加一次脉冲,以改变航天器的速度,从而进入和退出转移轨道。
- 初始变轨速度 ( Δ V 1 \Delta V_1 ΔV1):
Δ V 1 = G M r 1 ( 2 r 2 r 1 + r 2 − 1 ) \Delta V_1 = \sqrt{\frac{GM}{r_1}} \left( \sqrt{\frac{2r_2}{r_1 + r_2}} - 1 \right) ΔV1=r1GM(r1+r22r2−1)
- 目标变轨速度 ( Δ V 2 \Delta V_2 ΔV2):
Δ V 2 = G M r 2 ( 1 − 2 r 1 r 1 + r 2 ) \Delta V_2 = \sqrt{\frac{GM}{r_2}} \left( 1 - \sqrt{\frac{2r_1}{r_1 + r_2}} \right) ΔV2=r2GM(1−r1+r22r1)
其中, G G G 是引力常数, M M M 是中央天体的质量, r 1 r_1 r1 和 r 2 r_2 r2 分别是初始轨道和目标轨道的半径。
- 总变轨需求 ( Δ V t o t a l \Delta V_{total} ΔVtotal):
Δ V t o t a l = ∣ Δ V 1 ∣ + ∣ Δ V 2 ∣ \Delta V_{total} = |\Delta V_1| + |\Delta V_2| ΔVtotal=∣ΔV1∣+∣ΔV2∣
3. 转移时间的计算
霍曼转移的转移时间 ( T T T) 是从初始轨道进入转移轨道到达目标轨道所需的时间。根据开普勒第三定律,转移时间为转移轨道半周期的一半:
T = π G M a t 3 / 2 T = \frac{\pi}{\sqrt{GM}} a_t^{3/2} T=GMπat3/2
公式解释
- Δ V 1 \Delta V_1 ΔV1 和 Δ V 2 \Delta V_2 ΔV2: 这两个速度变化量分别用于从初始轨道进入转移轨道和从转移轨道进入目标轨道。通过这两个脉冲,航天器的轨道形状和能量得以调整,实现轨道转移。
- 总变轨需求 Δ V t o t a l \Delta V_{total} ΔVtotal: 这是完成霍曼转移所需的总速度变化量,反映了转移过程的燃料消耗情况。较小的 Δ V \Delta V ΔV 意味着更高的燃料效率。
- 转移时间 T T T: 这表示完成一次霍曼转移所需的时间,对于时间敏感的任务来说,转移时间是一个重要的考量因素。
应用实例
以从地球轨道转移到火星轨道为例,假设:
- 地球轨道半径 r 1 = 1 r_1 = 1 r1=1 天文单位(AU)
- 火星轨道半径 r 2 = 1.524 r_2 = 1.524 r2=1.524 AU
- 太阳质量 M = 1.989 × 1 0 30 kg M = 1.989 \times 10^{30} \, \text{kg} M=1.989×1030kg
- 引力常数 G = 6.674 × 1 0 − 11 m 3 kg − 1 s − 2 G = 6.674 \times 10^{-11} \, \text{m}^3 \text{kg}^{-1} \text{s}^{-2} G=6.674×10−11m3kg−1s−2
步骤 1:计算转移轨道半长轴
a t = 1 + 1.524 2 = 1.262 AU a_t = \frac{1 + 1.524}{2} = 1.262 \, \text{AU} at=21+1.524=1.262AU
步骤 2:计算所需的变轨速度
- 初始变轨速度:
Δ V 1 = G M 1 AU ( 2 × 1.524 1 + 1.524 − 1 ) ≈ 2.94 km/s \Delta V_1 = \sqrt{\frac{GM}{1 \, \text{AU}}} \left( \sqrt{\frac{2 \times 1.524}{1 + 1.524}} - 1 \right) \approx 2.94 \, \text{km/s} ΔV1=1AUGM(1+1.5242×1.524−1)≈2.94km/s
- 目标变轨速度:
Δ V 2 = G M 1.524 AU ( 1 − 2 × 1 1 + 1.524 ) ≈ 2.65 km/s \Delta V_2 = \sqrt{\frac{GM}{1.524 \, \text{AU}}} \left( 1 - \sqrt{\frac{2 \times 1}{1 + 1.524}} \right) \approx 2.65 \, \text{km/s} ΔV2=1.524AUGM(1−1+1.5242×1)≈2.65km/s
- 总变轨需求:
Δ V t o t a l = 2.94 + 2.65 = 5.59 km/s \Delta V_{total} = 2.94 + 2.65 = 5.59 \, \text{km/s} ΔVtotal=2.94+2.65=5.59km/s
步骤 3:计算转移时间
T = π G M ( 1.262 AU ) 3 / 2 ≈ 259 天 T = \frac{\pi}{\sqrt{GM}} (1.262 \, \text{AU})^{3/2} \approx 259 \, \text{天} T=GMπ(1.262AU)3/2≈259天
因此,从地球到火星的霍曼转移大约需要259天,所需的总变轨速度约为5.59 km/s。
霍曼转移方法的优缺点
优点:
- 燃料效率高: 霍曼转移轨道是两个圆形轨道之间最省燃料的轨道转移方法之一。
- 计算简单: 公式推导和实施相对简单,易于在实际任务中应用。
- 广泛应用: 被广泛应用于卫星部署、行星探测等多个领域,验证了其有效性。
缺点:
- 转移时间较长: 相对于某些其他转移方法,霍曼转移的转移时间较长,不适合时间敏感的任务。
- 发射窗口受限: 需要在特定的发射窗口进行,以确保初始和目标轨道的相对位置合适。
- 不适用于多重转移: 对于需要多次转移或复杂轨道调整的任务,霍曼转移可能不够灵活。
结论
霍曼转移方法作为轨道力学中的基石理论,以其高效的燃料利用率和相对简单的实施过程,在航天任务中扮演着重要角色。尽管存在转移时间长和发射窗口受限等缺点,霍曼转移仍然是许多卫星部署和行星探测任务的首选方法。随着航天技术的发展,更加高效和灵活的轨道转移方法也在不断被探索和应用,但霍曼转移的方法论依然为后续的发展奠定了坚实的基础。
相关文章:

霍曼转移方法介绍
霍曼转移方法介绍 背景 在航天工程中,轨道转移是指航天器从一个轨道移动到另一个轨道的过程。为了高效利用燃料并缩短转移时间,科学家们开发了多种轨道转移方法。其中,霍曼转移(Hohmann Transfer)因其燃料效率高、计…...

我的创作之路:机缘、收获、日常与未来的憧憬
目录 前言机缘收获 日常成就一个优化后的二分查找实现 憧憬 前言 每个人的成长旅程都有它独特的轨迹,而我的这段技术创作之路,则源于一次再普通不过的项目分享。 机缘 一切的开始其实是偶然。在一次项目中,我遇到了一个棘手的问题…...
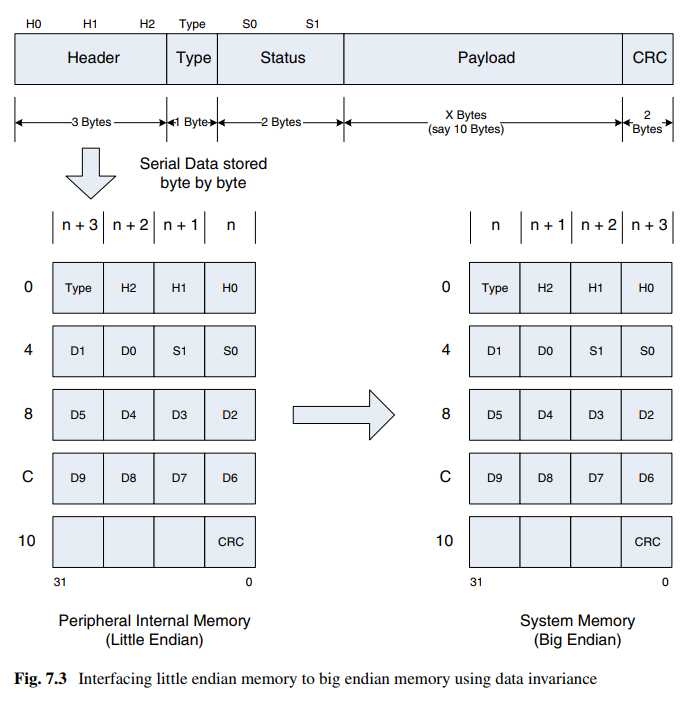
《硬件架构的艺术》笔记(六):处理字节顺序
介绍 本章主要介绍字节顺序的的基本规则。(感觉偏软件了,不知道为啥那么会放进《硬件架构的艺术》这本书)。 定义 字节顺序定义数据在计算机系统中的存储格式,描述存储器中的MSB和LSB的位置。对于数据始终以32位形式保存在存储器…...

AddIPAddress添加临时IP后,socket bind失败
问题描述 在Win10\Win11下使用addIPAddress添加临时IP成功后,立即创建socket,bind失败 if(!m_socket->bind(QHostAddress(m_localIP), listenPort)) {qCritical() << QString("bind error %1").arg(m_socket->errorString());re…...

关于IDE的相关知识之一【使用技巧】
成长路上不孤单😊😊😊😊😊😊 【14后😊///C爱好者😊///持续分享所学😊///如有需要欢迎收藏转发///😊】 今日分享关于ide使用技巧的相关内容! 关于…...

线性代数在人工智能领域中的实践
一、机器学习中的线性代数应用 在机器学习中,线性代数主要用于构建和训练各种模型,如线性回归、逻辑回归、支持向量机等。这些模型在数据的特征提取、降维处理以及分类等方面发挥了重要作用。 线性回归:线性回归是最简单的机器学习算法之一…...

图片生成视频-右进
右侧进入 ffmpeg -loop 1 -i image.jpg -f lavfi -i colorcblack:s1280x720:d20 -filter_complex "[1:v]formatrgba[bg];[0:v]formatrgba,scale1280:720[img];[bg][img]overlayxif(lt(t,3),W,if(lt(t,8),W-(t-3)*W/5,0)):y(H-h)/2:enablegte(t,3)" -c:v libx264 -t 2…...

3、集线器、交换机、路由器、ip的关系。
集线器、交换机、路由器三者的关系 1、集线器2、交换机(每个交换机是不同的广播域,ip地址起到划分广播域的作用)3、 路由器4、ip地址 所有图片和资料均来源于B站:网络安全收藏家 1、集线器 一开始两台电脑通信就需要网线就可以&a…...

w~视觉~合集25
我自己的原文哦~ https://blog.51cto.com/whaosoft/12627822 #Mean Shift 简单的介绍 Mean Shift 的数学原理和代码实现,基于均值漂移法 Mean Shift 的图像分割 Mean Shift 算法简介 从分割到聚类 对于图像分割算法,一个视角就是将图像中的某些点集分为一类&a…...

Applicaiton配置文件
server:port: 8080 # 配置 Spring Boot 启动端口,默认为 8080mybatis-plus:mapper-locations: classpath:com/xtl/mapper/xml/*.xml # 指定 MyBatis Mapper XML 文件的路径,确保 MyBatis 能够正确加载 Mapper 文件global-config:db-config:id-type: au…...

(已解决)wps无法加载此加载项程序mathpage.wll
今天,在安装Mathtype的时候遇到了点问题,如图所示 尝试了网上的方法,将C:\Users\Liai_\AppData\Roaming\Microsoft\Word\STARTUP路径中的替换为32位的Mathtype加载项。但此时,word又出现了问题 后来知道了,这是因为64位…...

ubity3D基础
Unity是一个流行的游戏开发引擎,它使用C#作为其主要的编程语言。以下是一些Unity中C#编程的基础概念: • Unity编辑器: • Unity编辑器是Unity游戏引擎的核心,提供了一个可视化界面,用于创建和管理游戏项目。 • C#脚本…...

Python2和Python3的区别
和python 2.x相比,python 3.x版本在语句输出、编码、运算和异常等方面做出了一些调整,我们这篇文章就对这些调整做一个简单的介绍。 Python3.x print函数代替了print语句 在python 2.x中,输出数据使用的是print语句,例如ÿ…...

Spring框架整合单元测试
目录 一、配置文件方式 1.导入依赖 2.编写类和方法 3.配置文件applicationContext-test.xml 4.测试类 5.运行结果 二、全注解方式 1.编写类和方法 2.配置类 3.测试类 4.运行结果 每次进行单元测试的时候,都需要编写创建工厂,加载配置文件等相关…...

docker-mysql
一、创建mysql 1、docker run --name mysql8.0-container -e MYSQL_ROOT_PASSWORDmy-secret-pw -d -p 3306:3306 mysql:8.0 参数解释: --name mysql8.0-container:指定容器的名称为mysql8.0-container。 -e MYSQL_ROOT_PASSWORDmy-secret-pw:…...

Java程序基础⑤Java数组的定义和使用+引用的概念
目录 1. Java数组的基本概念 1.1 数组的定义 1.2 数组存在的意义 1.3 数组的使用 1.4 二维数组 2. 引用类型JVM的内存分布 2.1 JVM的内存分布 2.2 基本数据类型和引用型数据类型的区别 2.3 引用注意事项 2.4 传值传递 3. 数组总结和应用场景 3.1 一维数组和二维数组…...

electron主进程和渲染进程之间的通信
主进程 (main.js) const { app, BrowserWindow, ipcMain } require("electron"); const path require("node:path"); // 导入fs模块 const fs require("fs");const createWindow () > {const win new BrowserWindow({width: 800,height…...

uniapp 安卓和ios震动方法,支持息屏和后台震动,ios和安卓均通过测试
最近使用uniapp开发震动功能,发现uniapp提供的 uni.vibrateLong()的方法震动比较弱,而且不支持息屏和后台震动。plus.ios.importClass("UIImpactFeedbackGenerator")是在网上看到的,这个震动也比较弱,ios也不支持息屏和…...

# DBeaver 连接hive数仓
前提 前提是基于hadoop的hive服务已经启动,其中hive的服务包括metastore元数据服务和hiveserver2服务已经启动。hiveserver2服务在默认端口10000启动,且通过telnet xx.xx.xx.xx 10000 能通。 满足以上要求后,再可以看以下连接文档ÿ…...
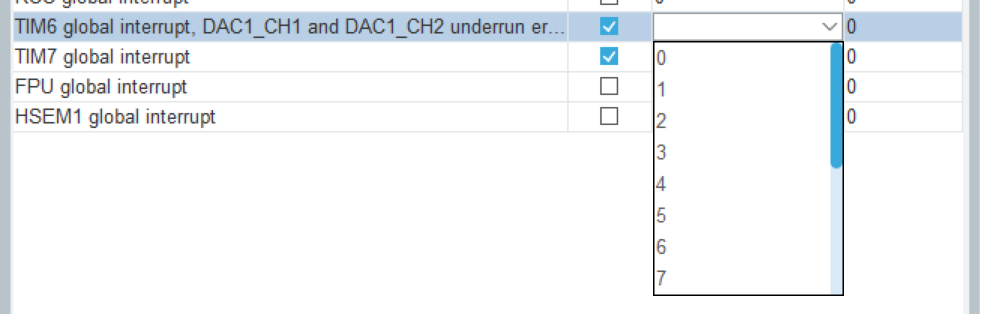
STM32H7开发笔记(2)——H7外设之多路定时器中断
STM32H7开发笔记(2)——H7外设之多路定时器中断 文章目录 STM32H7开发笔记(2)——H7外设之多路定时器中断0.引言1.CubeMX配置2.软件编写 0.引言 本文PC端采用Win11STM32CubeMX4.1.0.0Keil5.24.2的配置,硬件使用STM32H…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
